基于VFF-RLS的力传感器的动态特性研究
姚斌 张子豪 代煜 张建勋
基于VFF-RLS的力传感器的动态特性研究
姚斌 张子豪 代煜†张建勋
(南开大学 人工智能学院/机器人与信息自动化研究所,天津 300350)
在科学实验与工业生产中,力传感器动态特性会直接影响传感器的精度,因此研究力传感器动态特性具有重要意义。针对应用于手术机器人的应变式力传感器动态特性难以满足精度要求的问题,文中研究了基于最小二乘参数辨识方法在力传感器振动结构中的应用。由于递推最小二乘(RLS)对于二阶振动系统模型辨识难以同时保证快速性和抗干扰性,文中提出了一种基于可变遗忘因子的递推最小二乘参数辨识方法。首先,通过建立随机振动系统模型,对系统的输入/输出特性进行仿真与分析,确定了遗忘因子函数中的参数,仿真结果表明,文中提出的方法在保持更快收敛速度的同时,使参数辨识误差和收敛预测误差相比于RLS有明显的降低,相比于最小二乘有良好的时变性;然后,在阶跃测试标定法基础上对微创外科手术机器人力传感器的动态参数进行辨识,获得该传感器系统的结构动态特性,即固有频率和阻尼比。实验结果表明,文中提出的方法有较好的收敛性和稳定性,有效地提高了辨识精度。
遗忘因子;振动结构;动态性能标定;递推最小二乘;参数辨识
在许多工程应用中,振动结构作为力传感器的主体部分担任重要工作,了解其动态特性对于提高力传感器的精度具有重要意义[1]。为了能够获得更加准确的动态性能指标,需要针对具体应用场景、振动模型的结构选择合适的标定方法和辨识方法[2-4]。
目前国内外对力传感器中振动结构的动态性能标定方法的研究有很多[5-6]。Li等[7]设计了一种基于压电薄膜的力传感器并应用在钢球冷镦机中检测冷镦力,采用力锤冲击响应法进行动态标定实验实现对传感器系统固有频率的测量。Fu等[8]在电阻应变型多维力传感器的动态标定过程中,采用了在一定方向上加负阶跃的方式对力传感器进行动态校准,并根据系统的响应曲线进行了参数辨识。江文松等[9]通过落锤式冲击力校准装置获取激励与响应,利用最小二乘(LS)法实现了传递函数中参数的辨识。
对振动系统模型进行动态性能标定,首先要对振动模型施加阶跃激励[10-12]。然而,设计并搭建一个能够对具体振动系统模型施加激励信号的实验台,并没有一个统一的标准,需要结合具体情况具体分析,设计并制造一个高精度、结构简单、操作方便的实验台,能够给振动系统施加解耦的阶跃激励。文中针对实验使用的力传感器振动结构搭建了一个动态标定实验台。
对阶跃响应信号进行动态信号分析,一般采用频域分析路线,同时需要寻找一种合适的系统辨识方法对系统模型的动态性能参数进行辨识[13-14]。目前对系统参数进行辨识[2,15]的方法主要有阶跃响应法、最小二乘法、极大似然法[16]。另外,随着智能控制理论的发展,也出现了一些针对非线性系统的辨识方法,如神经网络、粒子群、遗传算法等智能辨识算法[17-18]。
阶跃响应法最为直观,根据阶跃响应时域曲线,能够大致计算出上升时间、自然频率、峰值时间等,利用阶跃响应曲线直接计算是二阶系统辨识最常见的方法,是简单且有效的分析系统性能的手段,然而该方法受主观因素和噪声的影响较大。极大似然辨识方法具有良好的渐进性和无偏性,褚式新等[19]基于辨识原理和前向差分提出了一种极大似然的辨识方法,能够获取无人艇操纵的二阶响应模型参数。但对于含有噪声的观测数据,该方法会明显影响参数估计的精度,且计算量较大。神经网络辨识方法具有非线性特性,可以实现非线性系统的建模。宋哲等[20]提出了基于神经网络的在线辨识方法,对压电悬臂梁结构的振动主动控制进行了研究,通过施加外扰激励进行系统的在线辨识,达到了对悬臂梁振动响应的良好控制作用。但神经网络辨识方法收敛速度慢,网络结构的确定没有一个具体的标准[21]。智能算法可以快速搜索高非线性、多维复杂空间,并且不受系统模型特性的限制。对于复杂系统,基于最小二乘的辨识方法在很多情况下是无能为力的,但对于线性振动模型,基于最小二乘的辨识方法运算简单、快速,开销小,在一定改进后能够克服估计有偏差的缺陷,故在很多实际工程中有广泛的应用[22-23]。
针对二阶振动模型的动态特性标定研究,文中提出了一种基于可变遗忘因子的递推最小二乘(VFF-RLS)的参数辨识方法,以便在参数辨识过程中可时刻调整新旧数据权重;然后在阶跃测试标定法基础上,对微创外科手术机器人力传感器的动态参数进行辨识,获得该传感器系统的结构动态特性,以验证所提方法的可行性。
1 动态标定方法
1.1 递推最小二乘(RLS)法
文中对多维力传感器线性振动系统模型进行分析,该系统模型一般被简化为标准二阶系统[7-9,22],域的系统模型可以表示为
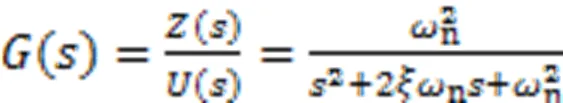
式中,()和()分别为零初始条件下输出信号和输入信号的拉氏变换,n为固有频率,为阻尼比。
针对线性振动模型的二阶传递函数进行离散化处理,可获得输入-输出的差分方程,确定待辨识的振动系统模型为
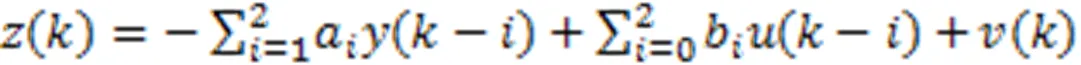
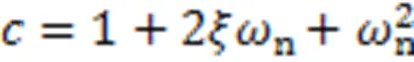
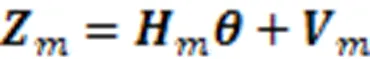

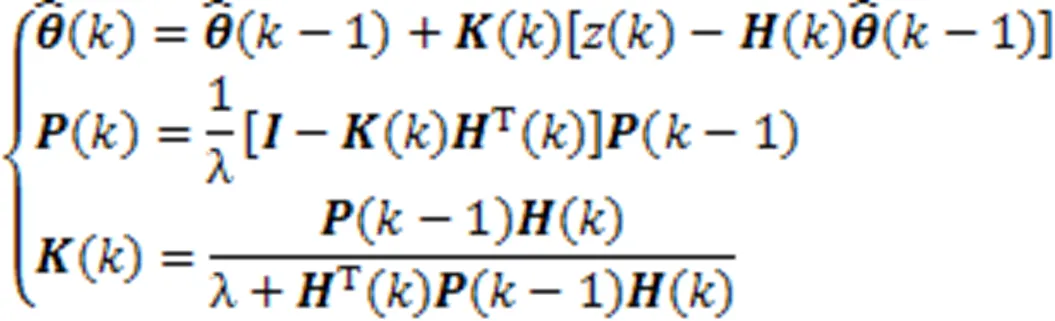
式中,k为当前时刻,当前参数估计值是根据预测误差对进行修正得到的,K为对估计值进行修正的增益矩阵,P为协方差矩阵,I为单位矩阵,λ为遗忘因子。基于RLS辨识方法的振动系统动态性能分析流程图如图1所示。
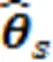
1.2 VFF-RLS法
在RLS的辨识过程中,遗忘因子=1是固定的,对于所有测量数据是不分优劣的,随着测量次数的增加和测量数据的不断增大,测量结果会趋于一致,参数的最小二乘估计依概率收敛于真值。当系统参数随时间变化时,新数据对估计值的修正被旧数据所掩盖。因此,相对于RLS,VFF-RLS参数辨识法引入动态遗忘因子调整新旧数据权重,能够提高算法收敛速度、跟踪速度以及降低估计误差。
定义时刻预测模型与实际模型的输出之差为预测误差(),表示为
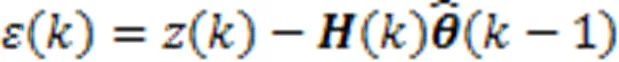
遗忘因子是参数估计函数的加权因子,在前一个参数估计结果基础上对预测误差的修正可以得到新的估计值[24],增益矩阵表示对预测误差的修正度,原则上越大对估计参数的修正效果越好,但由于最小二乘的一致性与无偏性,新数据的引入对参数无法起到修正作用,系统参数实时发生变化,引入遗忘因子就是动态调整新旧数据不同的权重,算法对于输入新的信息,或系统特性的变化做出快速的反应。因此的调整要受到()的影响,的初值选取影响到预测误差的收敛情况,将误差作为指数,参考文献[25],给出的表达式为
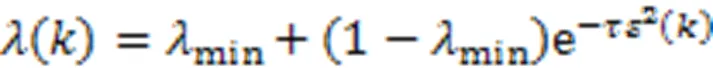
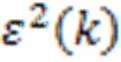
1.3 动态性能指标
振动系统模型可以视为标准二阶系统,其动态特性可以用阻尼比和固有频率n来描述,杆类振动系统是一种欠阻尼系统,对于欠阻尼系统只需将振动系统模型的参数向量转换为参数和n,就可以通过式(1)来描述振动系统的动态性能。
辨识出振动系统的模型参数后,振动系统的固有频率和阻尼比分别为
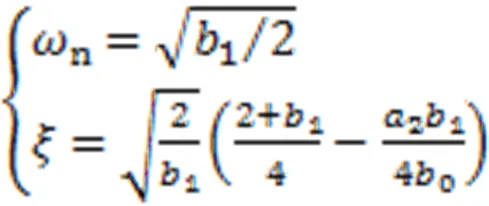
2 数值仿真
为了验证改进的RLS参数辨识方法的有效性以及准确性,文中首先按照基本二阶振动模型建立待辨识系统多项式(9),然后通过Matlab仿真对系统参数进行辨识,可以具体地量化分析辨识的准确性、快速性及误差的收敛性。
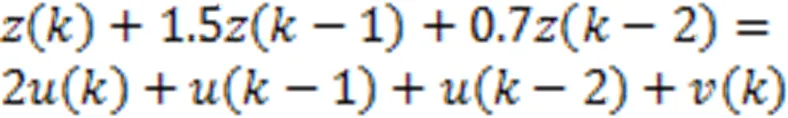
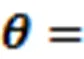
2.1 遗忘因子参数选取
遗忘因子λ的调整需要确定λ的初值以及调整系数τ,两个参数不同的取值会给准则函数带来不同的影响。λ过大会影响预测误差收敛速度,但参数收敛较快,而λ过小会导致参数估计波动过大,缺乏辨识精度,但预测误差会迅速收敛,所以遗忘因子初值不应过大或者过小。文中通过设定λ初值为0.99、0.95、0.85、0.80,分别观察4种初值情况下的估计参数变化与实际值的关系,结果如图2所示。从图中可知,在兼容参数快速收敛及抗噪声能力的情况下,若取0.95作为遗忘因子初值,则遗忘因子函数的变化从0.95开始进行动态调整,遗忘因子变化引起辨识参数的波动以及预测误差的震荡,又会动态地改变遗忘因子函数的取值,始终能够保证当新数据加入时,算法能够快速进行参数的辨识以及完成预测误差的收敛。
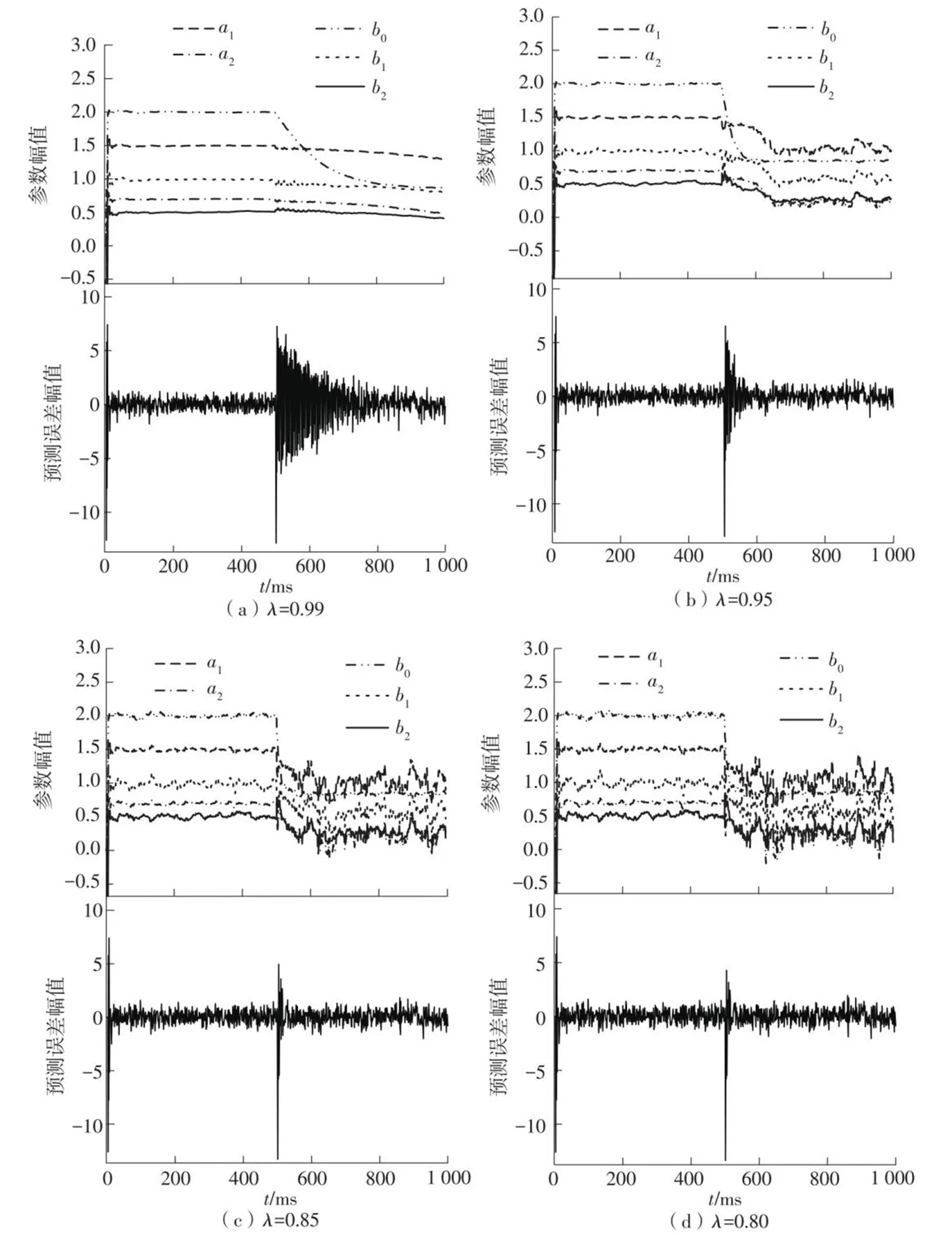
图2 遗忘因子对估计参数和预测误差的影响
调整系数的大小决定遗忘因子从初值趋近1的速率。为了使遗忘因子的变化区间始终分布于初值到1之间的有效区域,需要设置不同的,如图3所示。根据遗忘因子的变化情况,最终确定为3。
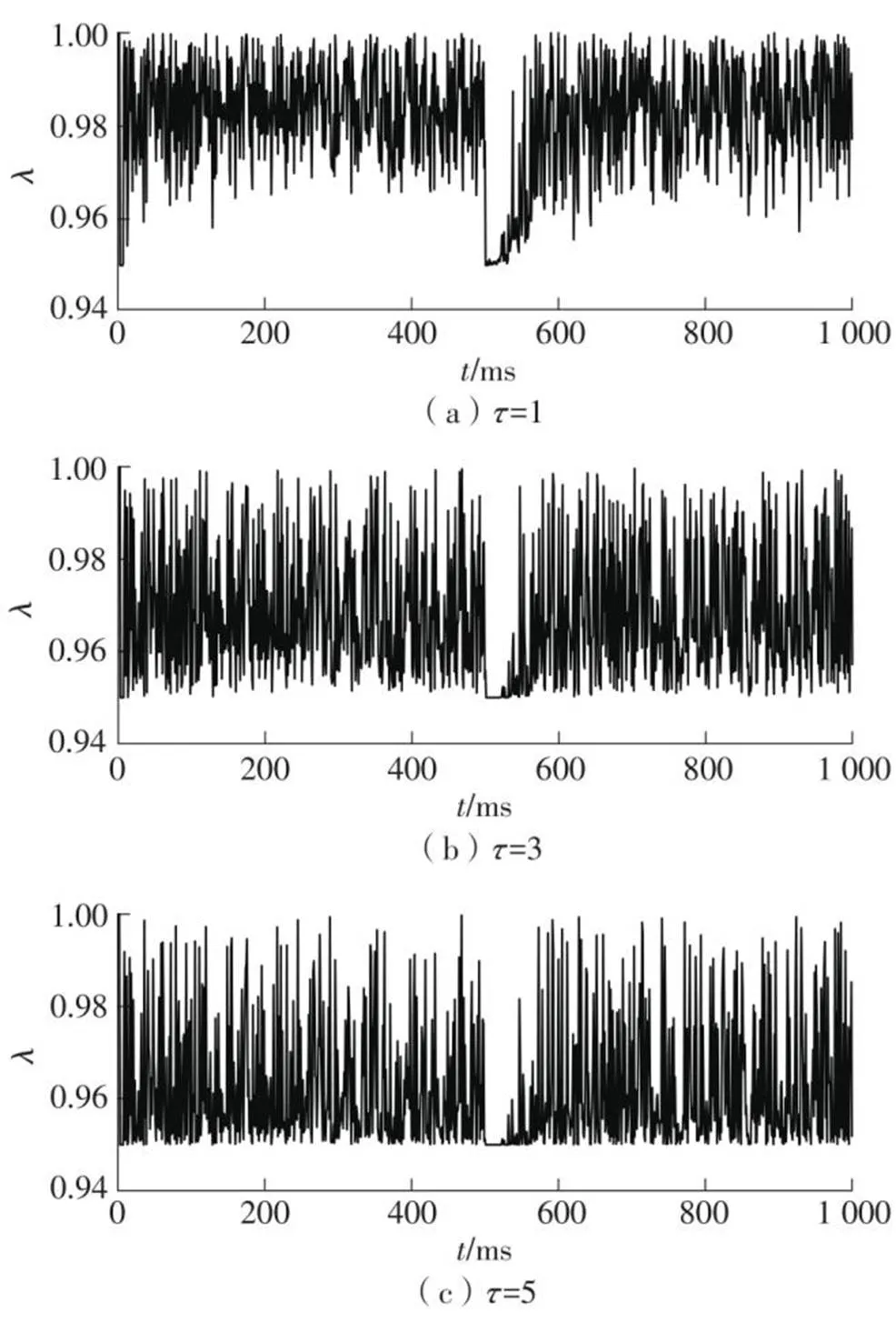
图3 τ取不同值时λ的变化
以上是对遗忘因子变化准则函数的初值选取,尽管辨识算法的收敛速度和误差精度主要还是取决于准则函数本身的特性,但增加对函数初值的分析和选取过程,能够帮助辨识算法更加高效。
2.2 仿真实验结果分析
采用文中提出的VFF-RLS辨识方法对仿真系统(9)进行辨识,结果如图4所示,与LS及RLS辨识结果的比较如表1所示。文中通过观察辨识参数的准确性、收敛速度以及预测误差的收敛速度,定义均方根误差(RMSE)来描述原始信号与辨识信号的相似度,用收敛过程经过的数据序列长度来描述算法的收敛速度。从表中可知,文中VFF-RLS方法的辨识效果明显优于RLS和LS方法。
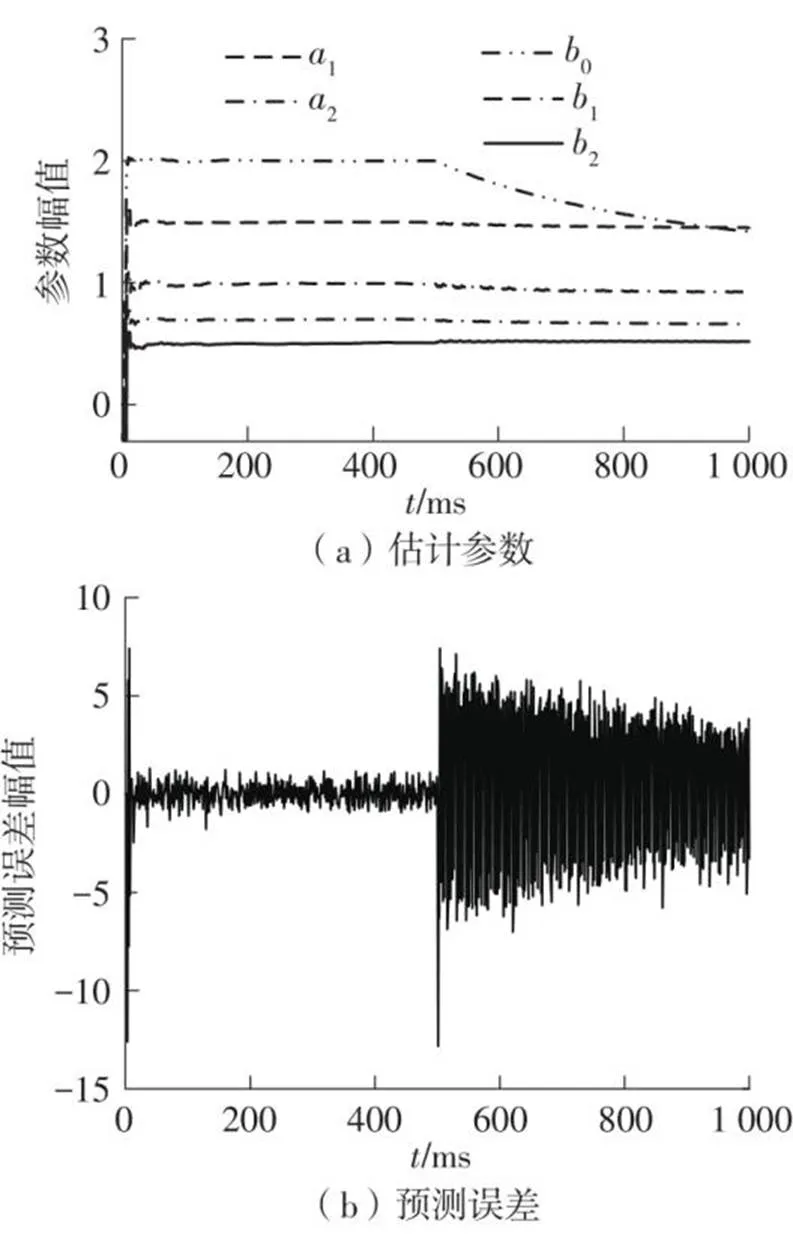
图4 VFF-RLS辨识方法的估计参数和预测误差
3 实验与结果分析
3.1 实验装置
文中实验对象是用于微创外科手术机器人的三维力传感器。该三维力传感器由应变计粘贴于钳形手术器械上构成,如图5所示。手术器械是“秒手”手术机器人的一部分,由天津大学等单位设计[26]。在使用微创手术机器人的手术器械时,是通过控制机械手的弹性杆末端的夹持机构对病人内脏进行缝合、打节及组织转移操作,在施加力时手术器械的弹性杆产生机械形变。力传感器振动系统模型的动态特性主要由受到激励后振动体的响应特性决定,将该弹性杆视为一个二阶的振动模型,对其进行动态标定测试更具可靠性。
表1 3种方法对仿真系统的辨识结果对比
Table 1 Comparison of identification results among three methods for the simulation system
辨识方法RMSE/%收敛速度 a1a2b0b1b2预测误差a1a2b0b1b2预测误差 LS1.510.701.990.990.517.03 RLS0.340.340.570.280.2111.49>500>500>500>500>500>500 VFF-RLS0.150.140.150.200.126.928016015515515057
力传感器的动态标定一般采用阶跃测试法、脉冲测试法和频率测试法。然而,采用频率测试法进行力传感器动态标定的实验,操作起来比较困难。而脉冲测试法也不适合对三维力传感器进行动态标定实验。结合现有的研究情况和实验操作的现实性,文中采用阶跃测试法对弹性杆进行动态标定实验。阶跃测试法操作简单且对弹性杆造成影响的人为因素较小,比较适合进行动态标定实验。
在手术器械远端的弹性杆上,沿轴向以120°间隔粘贴3枚金属应变计,用于检测弹性杆所受到的两个方向径向力和轴向力,如图5所示。所设计的三维力传感器存在维间耦合现象,因此本课题组对该力传感器进行了解耦方法的研究[21,27]。文中主要研究传感器的结构动态特性,因此将3枚应变计作为一个整体,忽略了应变计与各方向的对应关系。
为了对该三维力传感器的动态性能进行标定,设计了一个动态标定实验平台,如图6所示,该实验平台可以对三维力传感器在3个方向上单独施加激励信号,且3个方向力是完全解耦的。从而为采用阶跃测试法对传感器动态性能进行标定提供了一个可靠的实验平台。力传感器系统包括力传感器、信号调理电路。

图6 力传感器实验平台
手术器械通过夹持装置水平固定在标定台上。如图6(b)所示,细线的一端与负载砝码相连接,另一端固定在手术器械远端的施力帽上。通过剪断细线,负载砝码突然落下,由此产生一个负阶跃。标定过程为:①在空载情况下,通过调节信号采集电路板中信号调理电路的数字电位器大小来调节三维力传感器的零点,电路信息可参考文献[28];②悬挂一定质量的砝码,等待一段时间数据稳定后,剪断连接在施力帽和负载砝码之间的细线,使弹性杆末端的三维力传感器应变计产生机械形变;③通过设计的信号调理及采样电路将应变计的机械形变转换为电压信号;④上位机记录并存储采样电路传来的数据,导入到Matlab中进行数据分析和处理。
3.2 实验数据采集与分析
通常情况下,为了便于时域分析,可以将三维力传感器近似地等效为二阶系统,其回归传递函数如式(1)所示,可以用阻尼比和固有频率n等参数来描述其动态性能。三维力传感器是一种欠阻尼系统,因此文中只对欠阻尼情况下的二阶系统进行分析。
采用阶跃测试法分别对弹性杆的和方向进行动态标定。由于三维力传感器轴向(方向)的固有频率较高,且信号幅值微弱,不适合用作动态性能的分析。在实验中,放大器放大倍数为12 800,信号调理电路的低通滤波器截止频率为300 Hz,ADC采样频率为1 000 Hz,选择20 g的负载砝码,通过剪断细线分别得到两个方向的应力数据,、方向的衰减振动(阶跃)响应信号如图7所示。
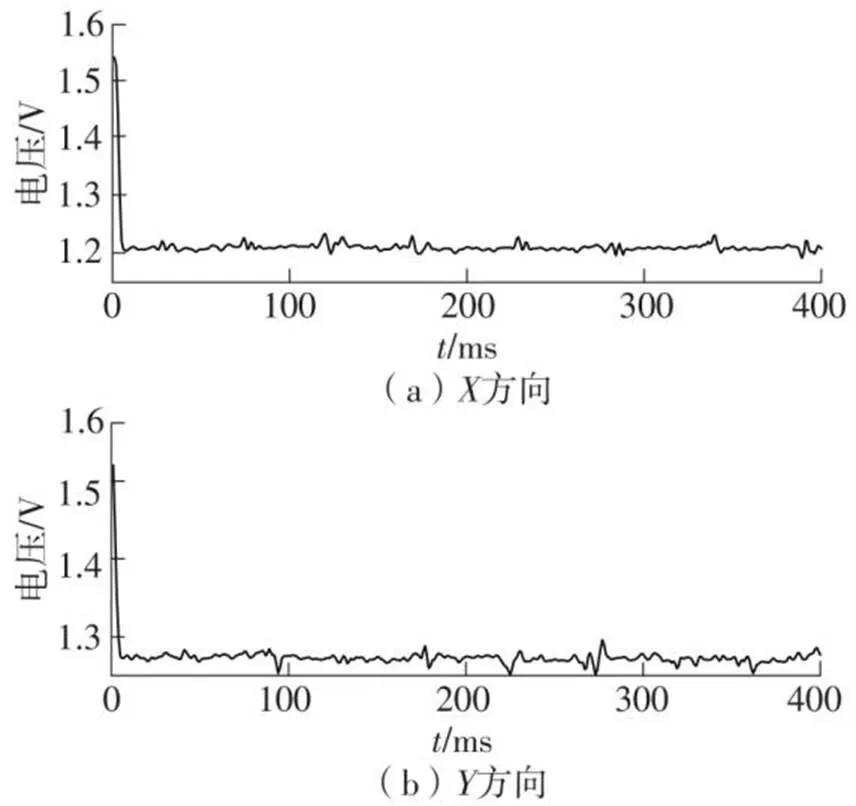
图7 振动系统的阶跃响应信号
采用文中所提的VFF-RLS方法对系统的动态性能参数进行辨识,结果如图8所示。按照辨识结果还原得到的辨识信号与阶跃响应信号对比如图9所示。将辨识参数结果按照式(8)进行计算,得到的弹性杆、方向的主要动态性能参数如表2所示。
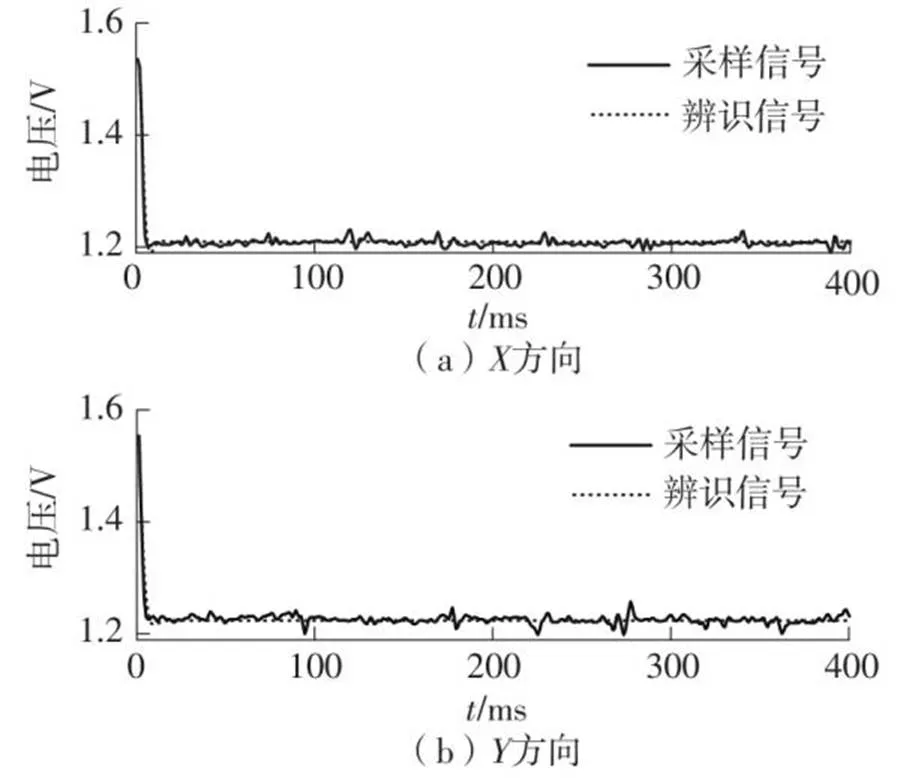
图9 阶跃响应信号与辨识信号
表2 三维力传感器的动态性能
Table 2 Dynamic performance of 3D force sensor
方向ωn/(rad·s-1)ξ X0.790.86 Y0.710.81
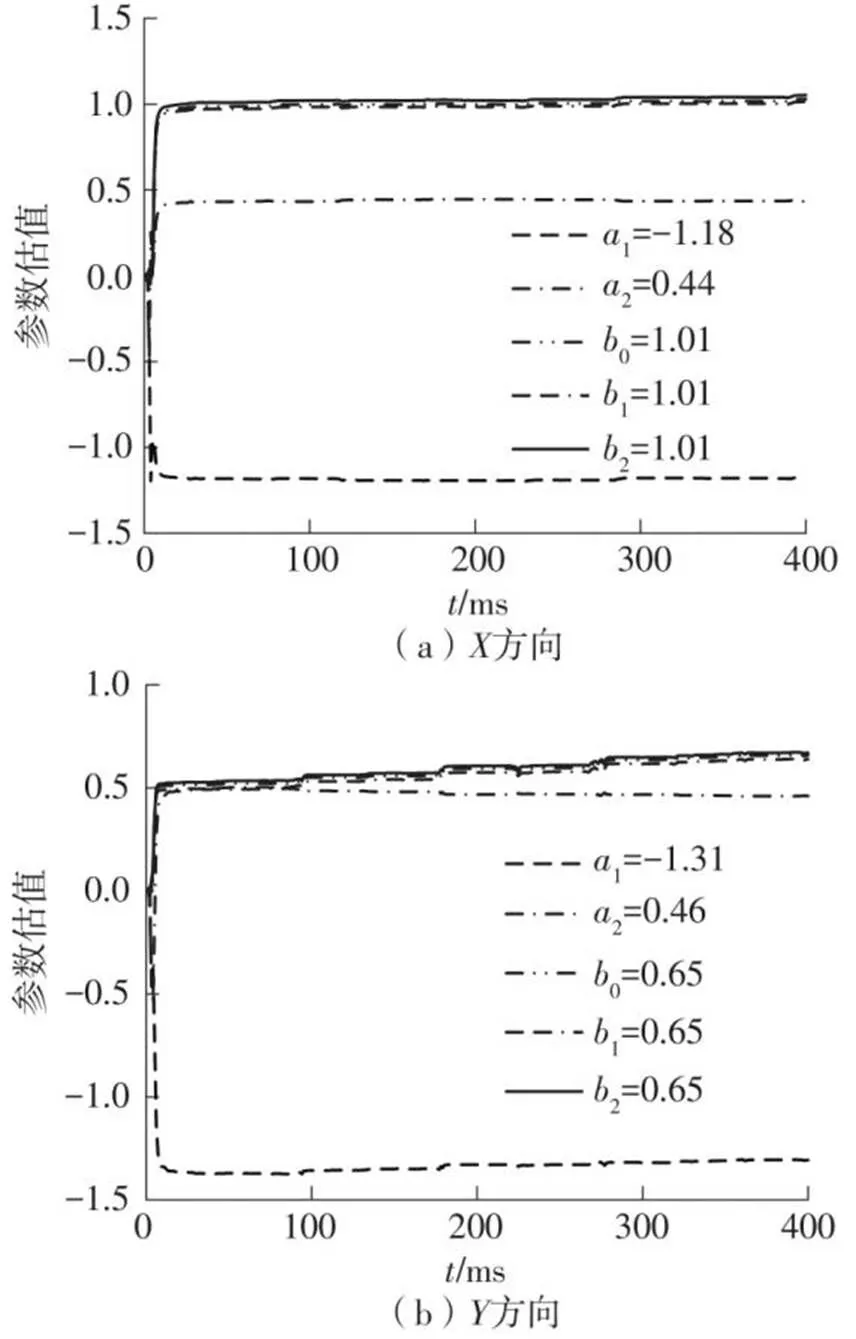
图8 VFF-RLS方法的参数辨识结果
4 结论
文中针对力传感器中振动结构模型,首先提出了基于可变遗忘因子的递推最小二乘参数辨识方法VFF-RLS,该方法通过引入遗忘因子来调整新旧信息的权重,并提出了一种遗忘因子的调整函数。数值仿真结果表明,VFF-RLS方法能够使辨识参数快速收敛,同时新数据的权重增大,预测误差也不会受到旧数据的太大影响。
然后,仿真构造一个二阶振动系统,通过对该二阶系统进行辨识,确定了遗忘因子初值和调整函数参数的大小,并比较了VFF-RLS方法与LS和RLS方法的参数辨识准确度、辨识收敛性、预测误差收敛性以及预测信号与实际信号的RMSE,结果表明,VFF-RLS方法的辨识效果明显优于RLS和LS方法。
最后,利用微创外科手术机器人的多维力传感器,设计了标定实验平台并利用VFF-RLS方法对该传感器的多个方向进行了动态特性参数辨识,得到系统模型多项式的系数向量,进而计算出该振动结构的动态性能指标。结果表明,VFF-RLS辨识方法的辨识速度快,辨识准确度较高,算法复杂度低。
[1] 谷向飞,孙松梅.六维力传感器静/动态性能指标综述[J].机械工程与自动化,2019(2):224-226.
GU Xiang-fei,SUN Song-mei.Summary of static/dynamic performance indexes of six-dimensional force sensor[J].Mechanical Engineering and Automation,2019(2):224-226.
[2] 张益瑞,苏建,徐观.三维测力装置维间耦合效应试验及解耦方法[J].华南理工大学学报(自然科学版),2021,49(5):135-144.
ZHANG Yirui,SU Jian,XU Guan.Research on coupling effect experiment and decoupling method of 3-D force measuring platform[J].Journal of South China University of Technology (Natural Science Edition),2021,49(5):135-144.
[3] 洪鹰,徐世超,肖聚亮,等.基于在线辨识的机器人惯量前馈控制仿真研究[J].天津大学学报(自然科学与工程技术版),2019,52(10):1069-1080.
HONG Ying,XU Shichao,XIAO Juliang,et al.Simulation study of robot inertia feedforward control based on online identification[J].Journal of Tianjin University (Science and Technology),2019,52(10):1069-1080.
[4] IDRISOV R,FLORIS I,ROTHHARDT M,et al.Characterization and calibration of shape sensors based on multicore optical fibre [J].Optical Fiber Technology,2021,61:102319/1-8.
[5] LIU S,QIN H,LIU Y,et al.Research on calibration test technology of multi-component force sensor[J].Journal of Physics:Conference Series,2021,1894:012011/1-8.
[6] MAHMOUD G M,OSMAN S M,HEGAZY R S.Proposed approach for force transducers classification[J].International Journal of Metrology and Quality Engineering,2021,12(1):1-7.
[7] LI Y-J,WANG G-C,CUI H-Y,et al.Dynamic characteristics and optimization research on PVDF piezoelectric film force sensor for steel ball cold heading machine[J].ISA Transactions,2019,94:265-275.
[8] FU L,SONG A.Model-based load characteristics analysis of the multi-dimensional force sensor[J].IEEE Access,2020,8:116431-116440.
[9] 江文松,尹肖,李泓洋,等.基于参数辨识的力传感器动态校准方法[J].计量学报,2021,42(5):603-608.
JIANG Wen-song,YIN Xiao,LI Hong-yang,et al.Dynamic calibration method of a force transducer based on parameter identification[J].Acta Metrologica Sinica,2021,42(5):603-608.
[10] 王嘉力.微型六维力/力矩传感器及其自动标定的研究[D].哈尔滨:哈尔滨工业大学,2007.
[11] MEDINA N,de VICENTE J.Force sensor characterization under sinusoidal excitations [J].Sensors,2014,14(10):18454-18473.
[12] YI J.Modelling and analysis of step response test for hydraulic automatic gauge control [J].Journal of Mechanical Engineering,2015,61(2):115-122.
[13] 张铁,覃彬彬,邹焱飚.机器人负载的动力学参数辨识[J].工程科学学报,2017,39(12):1907-1912.
ZHANG Tie,TAN Bin-bin,ZHOU Yan-biao.Identification methods for robot payload dynamical parameters[J].Chinese Journal of Engineering,2017,39(12):1907-1912.
[14] 车遥,周求湛,李大一,等.分子-电子感应式振动传感器传递函数辨识及频域特性分析[J].四川大学学报(工程科学版),2014,46(S1):177-181.
CHE Yao,ZHOU Qiuzhan,LI Dayi,et al.Transfer function identification and frequency domain analysis of the molecule electronic vibrating sensor[J].Journal of Sichuan University (Engineering Science Edition),2014,46(S1):177-181.
[15] 杨闪闪,殷鸣,徐雷,等.基于模态联合仿真寻优法的机床刀具结合部参数辨识方法[J].工程科学与技术,2019,51(3):198-204.
YANG Shanshan,YIN Ming,XU Lei,et al.Parameter identification of the tool shank based on the method of modal joint simulation optimization[J].Advanced Engineering Sciences,2019,51(3):198-204.
[16] EL-KAFAFY M,de TROYER T,GUILLAUME P.Fast maximum-likelihood identification of modal parameters with uncertainty intervals:a modal model formulation with enhanced residual term [J].Mechanical Systems and Signal Processing,2014,48(1/2):49-66.
[17] KOBELSKI A,OSINENKO P,STREIF S.Experimental verification of an online traction parameter identification method [J].Control Engineering Practice,2021,113:104837/1-11.
[18] XU B-C,ZHANG Y-Y.An improved gravitational search algorithm for dynamic neural network identification[J].International Journal of Automation and Computing,2014,11(4):434-440.
[19] 褚式新,茅云生,董早鹏,等.基于极大似然法的高速无人艇操纵响应模型参数辨识[J].兵工学报,2020,41(1):127-134.
CHU Shixin,MAO Yunsheng,DONG Zaopeng,et al.Parameter identification of high-speed USV maneuvering response model based on maximum likelihood algorithm[J].Acta Armamentarii,2020,41(1):127-134.
[20] 宋哲,陈文卿,徐志伟.基于神经网络的悬臂梁在线辨识与振动主动控制[J].振动与冲击,2013,32(21):204-208.
SONG Zhe,CHEN Wen-qing,XU Zhi-wei.Active vibration control of a cantilever beam based on neural network online identification[J].Journal of Vibration and Shock,2013,32(21):204-208.
[21] 姚斌,张建勋,代煜,等.用于微创外科手术机器人的多维力传感器解耦方法研究[J].仪器仪表学报,2020,41(1):147-153.
YAO Bin,ZHANG Jianxun,DAI Yu,et al.Research on decoupling method of multi-dimensional force sensor used in minimally invasive surgical robot[J].Chinese Journal of Scientific Instrument,2020,41(1):147-153.
[22] 代煜,孙和义,李慧鹏,等.基于小波变换的弱非线性阻尼和刚度辨识方法[J].振动与冲击,2009,28(2):51-55,200.
DAI Yu,SUN Heyi,LI Huipeng,et al.Identification of weak nonlinear ities on damping and stiffness based on wavelet transform[J].Journal of Vibration and Shock,2009,28(2):51-55,200.
[23] XU Z,ZHU G,ZHAO J,et al.Two-dimensional incremental recursive least squares identification for batch processes [J].Chemical Engineering Science,2021,237:116570/1-14.
[24] 谢文超,赵延明,方紫微,等.带可变遗忘因子递推最小二乘法的超级电容模组等效模型参数辨识方法[J].电工技术学报,2021,36(5):996-1005.
XIE Wenchao,ZHAO Yanming,FANG Ziwei,et al.Variable forgetting factor recursive least squales based parameter identification method for the equivalent circuit model of the supercapacitor cell module[J].Transactions of China Electrotechnical Society,2021,36(5):996-1005.
[25] SADIGH A N,YAZDI H S,HARATI A.Diversity-based diffusion robust RLS using adaptive forgetting factor [J].Signal Processing,2020,182:107950/1-12.
[26] WANG W,LI J,WANG S,et al.System design and animal experiment study of a novel minimally invasive surgical robot[J].International Journal of Medical Robotics Computer Assisted Surgery,2016,12(1):73-84.
[27] YAO B,ZHANG J,DAI Y,et al.Research on decoupling method of force sensor based on PSO-ELM[C]∥ Proeedings of 2020 Chinese Automation Congress.Shanghai:IEEE,2020:1016-1020.
[28] YAO B,DAI Y,XIA G,et al.High-sensitivity and wide-range resistance measurement based on self-balancing Wheatstone bridge and gated recurrent neural network[J].IEEE Transactions on Industrial Electronics,2023,70(5):5326-5335.
Research on Dynamic Characteristics of Force Sensor Based on VFF-RLS
(College of Artificial Intelligence/ Institute of Robotics and Automatic Information System,Nankai University,Tianjin 300350,China)
In scientific experiments and industrial production, the dynamic characteristics of the force sensor will directly affect the accuracy, so it is of great significance to research the dynamic characteristics of the force sensor. Aiming at the practical problem that the dynamic characteristics of strain gauge force sensor used in surgical robots are difficult to meet the accuracy requirements, this paper studied the application of least square parameter identification method in the vibration structure of force sensor. Because recursive least squares (RLS) is difficult to ensure the rapidity and anti-interference of the second order vibration system model identification, therefore, this paper proposed a recursive least squares parameter identification method based on variable forgetting factor. Firstly, the parameters of the forgetting factor function were determined by establishing the random vibration system model, simulating and analyzing the input/output characteristics of the system. The simulation results show that the proposed method in the paper can significantly reduce the parameter identification error and convergence prediction error compared with RLS while maintaining a faster convergence speed, and has better time variability compared with the least squares. Furthermore, the dynamic parameters of the force sensor used in minimally invasive surgical robot were identified based on the step test calibration method to obtain the structural dynamic characteristics (i.e. natural frequency and damping ratio) of the sensor system. The experimental results show that the proposed method in the paper has good convergence and stability, and can effectively improve the identification accuracy.
forgetting factor;vibration model;dynamic performance calibration;recursive least squares;parameter identification
Supported by the National Key R&D Program of China (2017YFC0110402)
10.12141/j.issn.1000-565X.220374
2022⁃06⁃15
国家重点研发计划项目(2017YFC0110402);天津市自然科学基金资助项目(1JCYBJC18800)
姚斌(1996-),男,博士生,主要从事手术机器人力感知及力反馈研究。E-mail:yaobin0317@foxmail.com
代煜(1981-),男,教授,博士生导师,主要从事医疗手术机器人研究。E-mail:daiyu@nankai.edu.cn
TN911.7
1000-565X(2023)05-0086-09

