基于稀疏脉冲采样的低复杂度血流速度估计算法
马碧云 吴港 刘娇蛟 范逸华
基于稀疏脉冲采样的低复杂度血流速度估计算法
马碧云 吴港 刘娇蛟 范逸华
(华南理工大学 电子与信息学院,广东 广州 510640)
双模超声广泛用于医学临床诊断,其中B模式脉冲用于成像,多普勒脉冲则用于血流速度估计。数据采集时间在两种模式之间共享。为了提高B模式图像的更新频率,需要减少多普勒脉冲数量,即发射稀疏多普勒脉冲进行血流速度估计。然而现有的适应稀疏脉冲采样算法,如迭代自适应算法、稀疏贝叶斯法以及基于阵列虚拟拓展的子空间类方法,计算开销巨大,难以满足实时成像的要求,且在稀疏度大的情况下会产生明显的伪影。为此,文中提出了一种基于稀疏脉冲采样的低复杂度血流速度估计算法。根据超声多普勒回波信号是由血红细胞的散射产生,具有强相干、信源个数时变的特点,文中首先从子空间角度解析了伪影的成因,并验证了包含均匀脉冲的稀疏发射脉冲排布方式可以有效地抑制伪影;然后以均匀脉冲回波构建协方差矩阵,并进行空间平滑获取特征值,以较大特征值的个数和相互的比值作为标准,判断血流不同时刻的频率分布特征;最后以此频率分布特征为标准,自适应采用B-MUSIC算法或TBVAM算法进行血流速度估计,以降低算法的复杂度。Matlab仿真和人体实测数据的实验结果表明,该算法在极大地减小计算复杂度的同时,可以获得较为连续、清晰且伪影抑制效果较佳的血流速度估计结果。
医学超声成像;血流速度估计;多普勒超声信号;稀疏采样
超声多普勒技术可以实现非介入式的血流速度估计[1],广泛用于临床诊断。医学超声系统采用双模发射,其中B模式脉冲用于成像,多普勒脉冲用于血流速度估计。数据采集时间在两种模式之间共享,需要合理地安排两者发射间隔和发射频次,即发射排布。为了提高B模式图像的更新频率,需要减少多普勒脉冲数量,即发射稀疏脉冲完成血流速度估计。因此,基于稀疏多普勒脉冲的血流速度高精度估计算法成为研究的热点[2]。
Gran等[3-4]提出了使用血流迭代自适应算法(BIAA)进行血流速度估计,这种方式可以处理任意排布的多普勒发射脉冲,但需要进行迭代运算,计算量大,且需使用回归滤波器去除杂波,会产生杂散频率分量而降低频谱估计的质量。为了进一步降低复杂度和提高计算精度,Lorintiu等[5]提出使用块稀疏贝叶斯学习(BSBL)方法进行血流速度估计,可采用随机排布多普勒发射脉冲,然而其计算开销巨大,且在稀疏度大的情况下会产生明显的伪影。为了抑制稀疏脉冲产生的伪影,Cohen等[6]利用多输入多输出雷达系统中嵌套阵列的研究成果,使用嵌套排布(NEST)的多普勒发射脉冲进行血流速度估计,提出了基于傅里叶变换的NEST和基于NEST的旋转不变性子空间算法(NESPRIT),用于血流速度估计。NEST具有较低的复杂性,并且在同等脉冲个数的情况下,由于使用了嵌套排布扩展了孔径,相较于以往的方法有更高的分辨率。NESPRIT由于采用了虚拟阵列技术,实现了较高分辨率的血流速度估计,但运算复杂度较高,仅在发射嵌套排布的稀疏多普勒脉冲时才可获得较好的估计效果,而其他的稀疏排布方式(如超嵌套排布、互质排布、四阶嵌套排布等)会产生严重的伪影,无法取得较好的估计结果,受限于其发射多普勒脉冲间隔,在相同稀疏发射情况下比经典Welch和Capon等方法[7-8]的计算复杂度高。
针对上述问题,为了在相同条件下获得比Welch等方法较高的分辨率,文中首先从子空间的角度解释了伪影的成因,并验证了一种抑制伪影的发射脉冲排布方式;然后根据血流回波不同时刻的频率分布特征,提出了一种可用于稀疏脉冲的自适应估计算法,并通过Matlab仿真和人体实测数据验证了该算法的有效性。
1 血流速度估计模型



对回波信号进行协方差运算,得到协方差矩阵
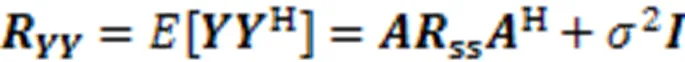




2 子空间类算法与伪影成因
基于谱估计的MUSIC算法,对协方差矩阵进行特征值分解,可以得到噪声子空间和信号子空间,即


于是可以通过频率范围内的搜索得到频谱,也就是血流速度谱,即

上述方法称为B-MUSIC算法。
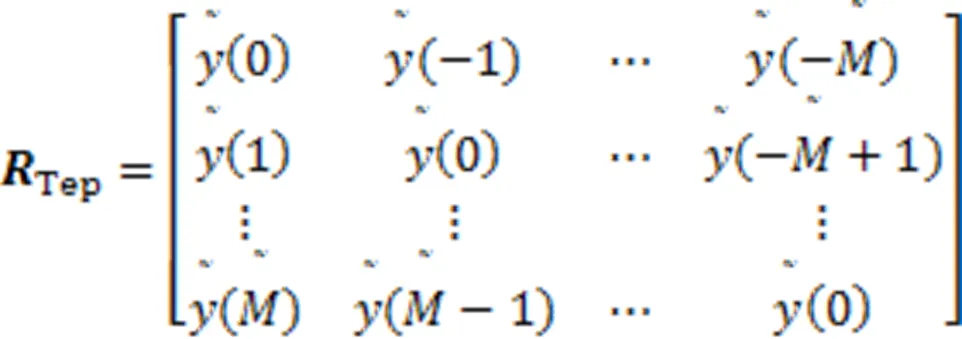

于是使用与B-MUSIC算法相似的步骤进行特征值分解,求得噪声子空间为

接着对其进行谱搜索,可得到血流速度谱
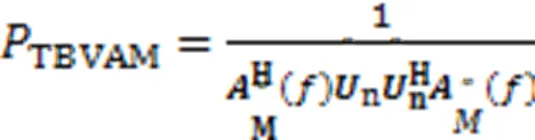
该方法称为TBVAM算法。
然而,除了嵌套排布外,稀疏发射脉冲排布使用各类算法均会出现伪影[6]。对于B-MUSIC算法,由于采样容积[10]的存在,回波还有多种频率分量,即多个信源。使用虚拟方式出现伪影,是由于频率分量过多,导致其估计是有偏的[11]。
若仅采用物理发射脉冲,从子空间角度出发,要抑制伪影最简单的方式就是让发射排布在前段有足够数量的单位间隔均匀脉冲。如果将流型矩阵简单划分为两部分,即
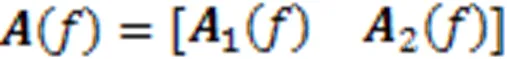


图1 第二峰值处的随均匀脉冲长度的变化
3 自适应血流速度估计

血流速度随着心跳呈现周期变化,当血流速度较小时,其回波频率分量会较为集中[12],此时伪影与实际血流速度估计谱很容易区分,在源数少的情况下,用B-MUSIC算法的估计性能比用虚拟阵列方法更优[13-14]。文中结合B-MUSIC和TBVAM算法的各自优势,提出了一种可以自适应血流流速变化的低复杂度稀疏脉冲血流速度估计算法BSEA。
首先,为了区分不同时刻的流速扩散情况,对均匀线阵处使用空间平滑,通过较大特征值的个数和相互的比值进行血流流速的判断。
以长度为128的单位间隔均匀线性排列为例,对1 s内血流信号进行空间平滑后以软阈值算子算法[15]进行信源个数估计,结果如图2所示,其信源个数随时间变化的规律与血流速度变化规律一致。

图2 软阈值算子算法的信源个数估计结果
从图2可以看出:对于血流速度较快区域,信源个数较多,即血流频率分量较多,进行特征分解会有较多较大的特征值;对于血流速度较慢的区域,频率分类较少,只有少量的大特征值。因此,可以对最大特征值与第二大特征值进行比较,若

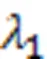

由式(6)进行特征值分解求特征值;
else
end if
4 仿真结果分析
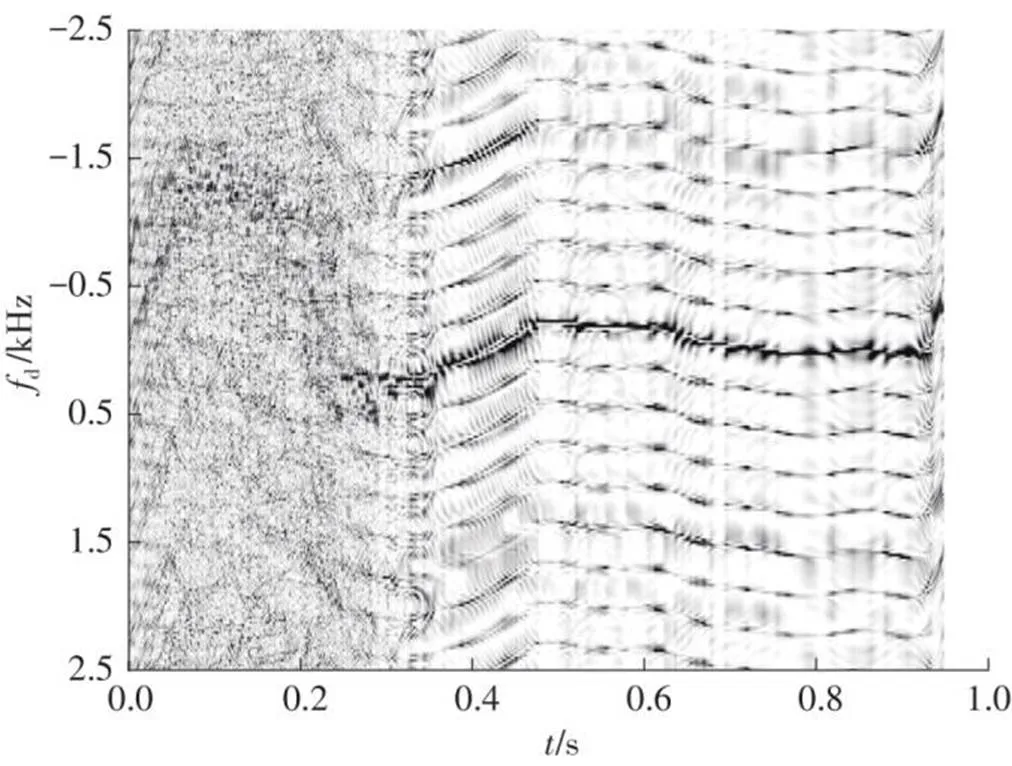
图3 最小冗余排布使用B-MUSIC算法的估计结果
对27个发射脉冲的最小冗余排布发射排序加上一个长度为16的发射间隔均匀线阵,其总的物理发射脉冲数为37。同时,为了防止由于物理发射脉冲数目的增加而提升估计性能,文中随机在27个发射脉冲的最小冗余排序中加入发射序列直至其达到37个物理脉冲。对这两种发射排布分别使用B-MUSIC算法与TBVAM算法进行血流速度估计,结果如图4所示。
从图4(a)和4(c)可以看出,采用B-MUSIC算法估计时,前端添加均匀线阵的伪影抑制效果明显优于随机添加发射脉冲。从图4(b)和4(d)可以看出,TBVAM算法相较于B-MUSIC算法,具有更好的伪影抑制效果,且估计精度更高,同时前端添加均匀脉冲会比随机添加发射脉冲有更好的伪影抑制性能。

采用前端添加均匀线阵的最小冗余排布,分别使用BSBL算法与BSEA算法进行血流速度估计,结果如图5所示。从图中可知,BSEA算法相对于同样可以用于稀疏阵列的BSBL算法,伪影抑制效果更优,且算法的估计精度更高,可与TBVAM算法的性能进行比较。此外,同样的仿真环境和稀疏发射脉冲排布,使用BSBL算法耗时为1 211.71 s,TBVAM算法耗时为28.41 s,而使用BSEA算法耗时为15.03 s,由此可见,使用BSEA算法可以有效地降低计算复杂度。
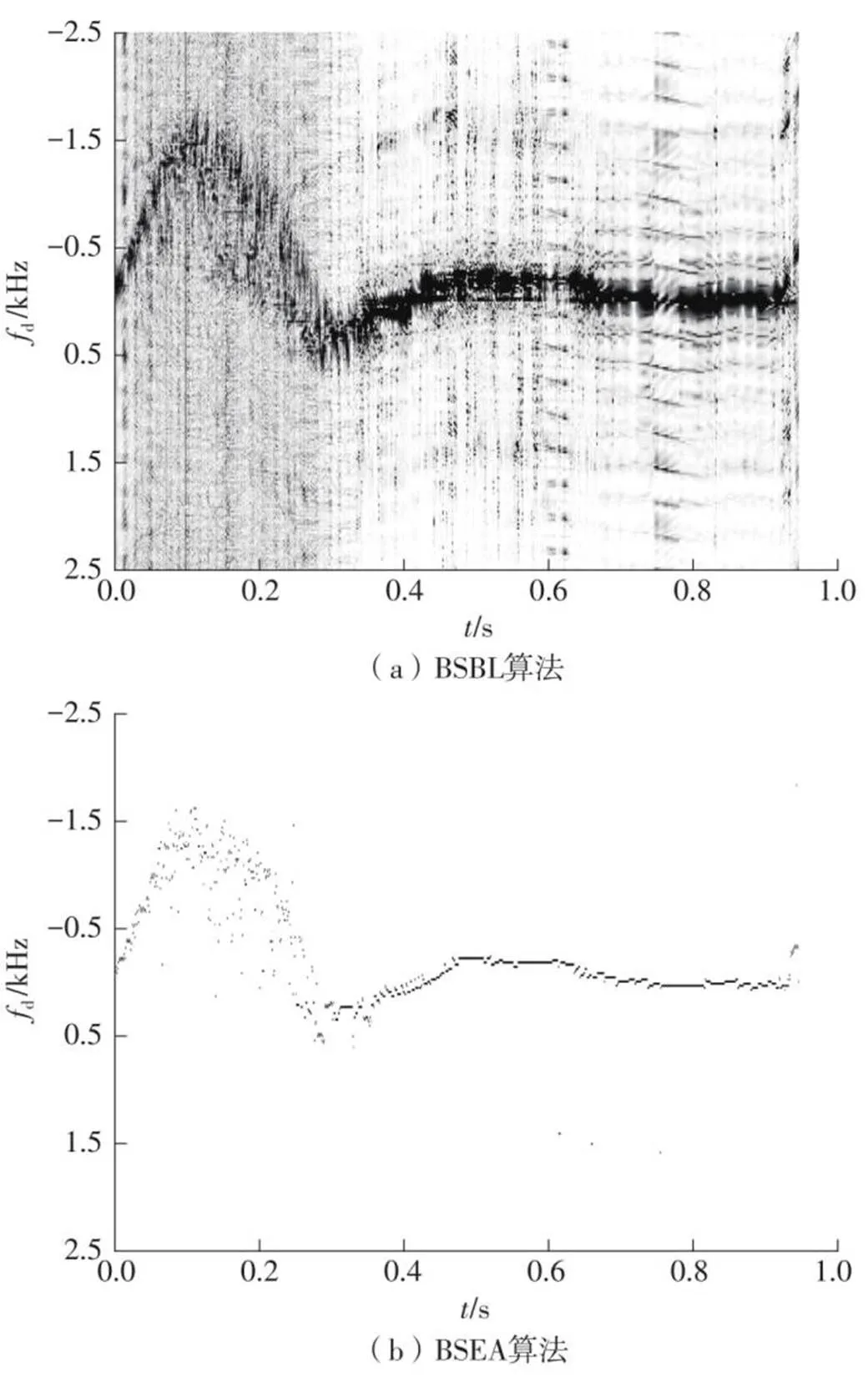
图5 最小冗余排布添加均匀脉冲后的估计结果
最后采用体超声多普勒回波的开源数据[6]验证文中BSEA算法的实用性。该数据来自于一位33岁的健康男性,探测部位分别为颈部主动脉和肝脏静脉。回波数据采集方式为:用B-K8556 3.2 MHz线性阵列探头进行扫描,脉冲重复发射频率为3.5 kHz,总脉冲个数为8 000,每个脉冲快拍数为128,采样频率15 MHz。首先对回波中由血管壁、组织反射所产生的低频杂波部分进行壁滤波[6,16],此处壁滤波选取巴特沃兹高通滤波器,其截止频率为80 Hz;然后进行Hilbert变换,将实信号变为复信号以便进行血流速度估计;接着采用27个发射脉冲的最小冗余排布发射排序加上一个长度为16的发射间隔均匀线阵作为发射排布,采用BSEA算法进行血流速度估计,结果如图6所示。实验结果表明,文中所提出的BSEA算法在实际应用中,尤其对于血流频率分量较多的动脉回波数据,可以获得较为连续、清晰且伪影抑制效果较佳的血流速度估计结果,具有实用性。
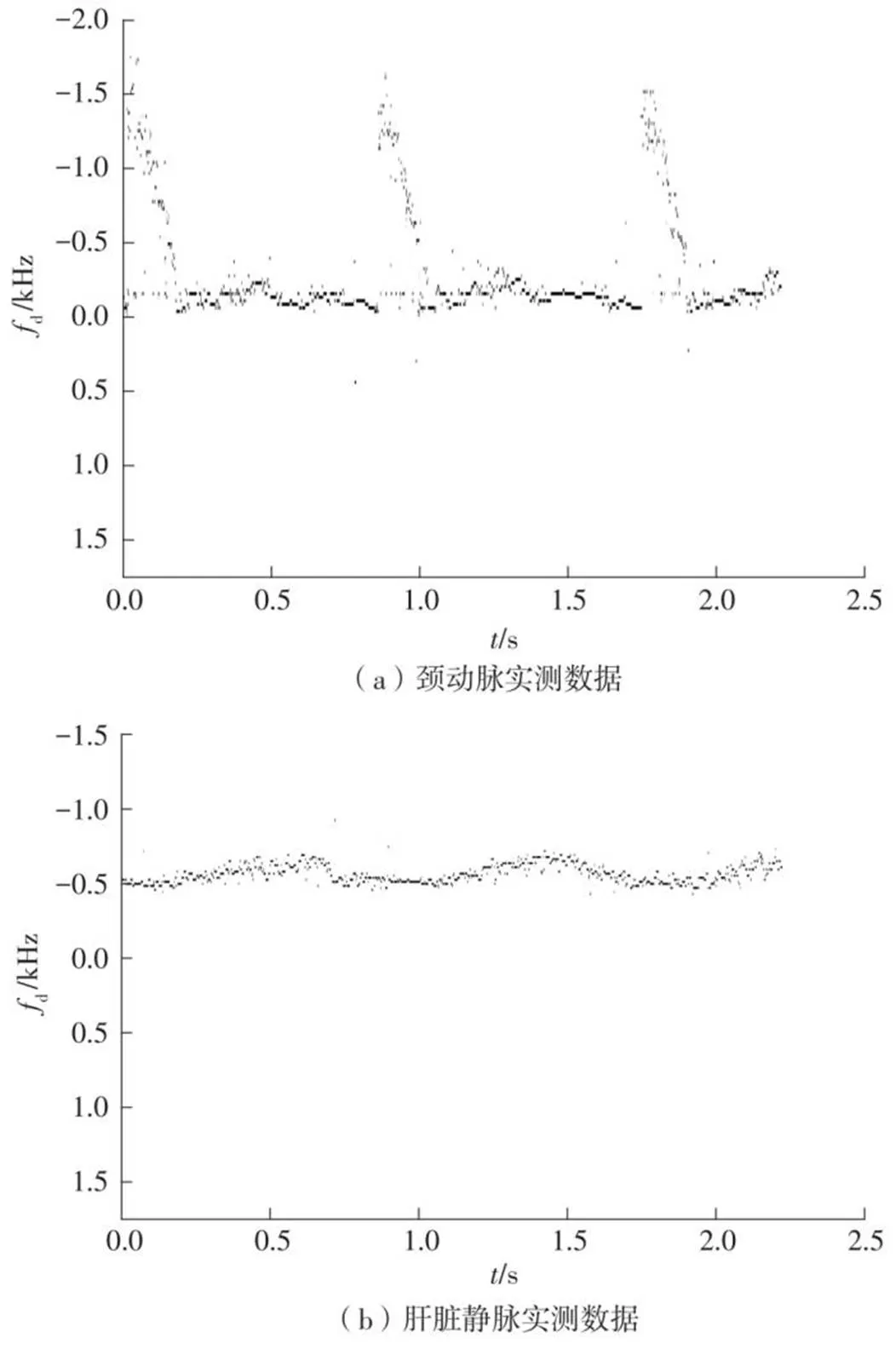
图6 BSEA算法的人体实测数据估计结果
5 结语
文中使用子空间方法分别基于直接稀疏发射脉冲排布以及虚拟化后的脉冲排布进行血流速度估计,从子空间的角度说明了当稀疏发射排布中存在一个均匀线阵时有助于抑制伪影。采用虚拟脉冲进行血流速度估计,既可以有效抑制伪影,也可以提高估计精度,但会大大增加运算复杂度。因此,文中提出了一种可用于稀疏脉冲的自适应估计算法BSEA,该算法可根据血流速度的时变性、流速较大时与流速较小时不同的频率分布特征,自适应采用B-MUSIC算法或TBVAM算法,以降低计算复杂度。Matlab仿真和人体数据血流速度估计结果表明,BSEA算法可在抑制伪影的同时,极大地减小计算复杂度。
[1] 赵冬冬,刘雪松,周凡,等.便携式三维成像声纳的非网格化稀疏阵列技术[J].华南理工大学学报(自然科学版),2019,47(2):24-30.
ZHAO Dongdong,LIU Xuesong,ZHOU Fan,et al.Nongrid sprse array technology for portable 3D imaging sonar[J].Journal of South China University of Technology(Natural Science Edition),2019,47(2):24-30.
[2] JENSEN J A,ARENDT J.Spectral velocity estimation in ultrasound using sparse data sets[J].The Journal of the Acoustical Society of America,2006,120(1):211-220.
[3] GRAN F,JAKOBSSON A,JENSEN J A.Adaptive spectral Doppler estimation[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,2009,56(4):700-714.
[4] GUDMUNDSON E,JAKOBSSON A,JENSEN J A,et al.Blood velocity estimation using ultrasound and spectral iterative adaptive approaches[J].Signal Processing,2011,91(5):1275-1283.
[5] LORINTIU O,LIEBGOTT H,FRIBOULET D.Compressed sensing Doppler ultrasound reconstruction using block sparse Bayesian learning[J].IEEE Transactions on Medical Imaging,2016,35(4):978-987.
[6] COHEN R,ELDAR Y C.Sparse Doppler sensing based on nested arrays[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,2018,65(12):2349-2364.
[7] WELCH P.The use of fast Fourier transform for the estimation of power spectra:a method based on time averaging over short,modified periodograms[J].IEEE Transactions on Audio and Electroacoustics,1967,15(2):70-73.
[8] TABATABAEI MAJD S M M,MOHAMMADZADEH ASL B.Adaptive spectral Doppler estimation based on the modified amplitude spectrum Capon[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,2021,68(5):1664-1675.
[9] LIU C L,VAIDYANATHAN P P.Remarks on the spatial smoothing step in coarray MUSIC[J].IEEE Signal Processing Letters,2015,22(9):1438-1442.
[10] AMBROGIO S,JANE A,ELIZABETH G,et al.Pulsed wave Doppler measurements of maximum velocity:dependence on sample volume size[J].Ultrasound in Medicine & Biology,2022,48(1):68-77.
[11] WANG M,NEHORAI A.Coarrays,MUSIC,and the Cramér-Rao bound[J].IEEE Transactions on Signal Processing,2017,65(4):933-946.
[12] 高莲,张榆锋,章克信,等.病变血管内血流分布模型的研究进展[J].系统仿真学报,2014,26(1):146-151.
GAO Lian,ZHANG Yu-feng,ZHANG Ke-xin,et al.Research progress of blood flow distribution models in diseased vessels[J].Journal of System Simulation,2014,26(1):146-151.
[13] VAIDYANATHAN P P,PAL P.Direct-MUSIC on sparse arrays[C]∥ Proceedings of 2012 International Conference on Signal Processing and Communications.Bangalore:IEEE,2012:1-5.
[14] PAL P,VAIDYANATHAN P P.Gridless methods for underdetermined source estimation[C]∥ Proceedings of the 48th Asilomar Conference on Signals,Systems and Computers.Pacific Grove:IEEE,2014:111-115.
[15] PAL P,VAIDYANATHAN P P.Soft-thresholding for spectrum sensing with coprime samplers[C]∥ Proceedings of 2014 IEEE the 8th Sensor Array Multichannel Signal Processing Workshop.A Coruna:IEEE,2014:517-520.
[16] 王录涛,王微,金钢.基于Hankel-SVD的非平稳超声血流成像杂波抑制技术研究[J].电子与信息学报,2015,37(4):830-835.
WANG Lu-tao,WANG Wei,JIN Gang.Non-stationary clutter rejection based on Hankel-SVD for ultrasound color flow imaging[J].Journal of Electronics and Information Technology,2015,37(4):830-835.
Low Complexity Blood Flow Velocity Estimation Algorithm via Sparse Pulse Sampling
(School of Electronic and Information Engineering,South China University of Technology,Guangzhou 510640,Guangdong,China)
Dual-mode ultrasound is widely used in medical clinical diagnosis. The B-mode pulse is used for imaging and Doppler pulse is used for blood flow velocity estimation. The data collection time is shared between the two modes. To improve the update frequency of B-mode image, it is necessary to reduce the number of Doppler pulses, that is, to estimate the blood flow velocity by sparse Doppler emissions. However, the existing algorithms for sparse pulse sampling, such as iterative adaptive algorithm, sparse Bayesian algorithm and subspace method based on array virtual expansion, are huge in expense and can not meet the requirements of real-time imaging. What’s more, they will lead to obvious artifacts in the case of large sparsity. Therefore, this paper proposed a low complexity blood flow velocity estimation algorithm via sparse pulse sampling. Based on the fact that ultrasonic Doppler echo signal is generated by the scattering of red blood cells, so echoes are strong coherence signals with time-variation sources number, this paper firstly explained the cause of artifacts from the perspective of subspace, and verified that the sparse emission pulse arrangement with uniform pulse can effectively suppress artifacts. Then the covariance matrix was constructed with uniform pulse echo, and the eigenvalues were obtained after spatial smoothing. The frequency distribution characteristics of blood flow at different segments were derived by the number of larger eigenvalues and the ratio of each other. Finally, based on the frequency distribution characteristics, the B-MUSIC algorithm or TBVAM algorithm was adaptively used for blood flow velocity estimation to reduce the complexity of the algorithm. The experimental results with Matlab simulation and human body measurement data show that the algorithm can obtain continuous, clear blood flow velocity estimation results with well artifact suppression while reducing the computational complexity significantly.
medical ultrasound imaging;blood velocity estimation;Doppler ultrasound signal;sparse sampling
Supported by the General Program of the Natural Science Foundation of Guangdong Province (2021A1515011842,2022A1515011830,2023A1515011420)
10.12141/j.issn.1000-565X.220380
2022⁃06⁃17
广东省自然科学基金面上项目(2021A1515011842,2022A1515011830,2023A1515011420);广州市科技计划项目(202102080352)
马碧云(1982-),女,博士,副教授,主要从事超声检测、超声通信研究。E-mail:eebyma@scut.edu
TP391.41;R445.1
1000-565X(2023)05-0063-07

