基于复杂网络理论的预警系统结构建模与分析
李耀东,肖 兵,杨 平,李 争
(1.空军预警学院,武汉 430000;2.解放军94981 部队,南昌 330000)
0 引言
预警系统作为联合作战体系的重要组成部分,直接支持战略决策和作战行动。一直以来,世界各军事强国都将其作为国防力量建设的重点工程。目前,我国的预警系统发展逐步整合“陆、海、空、天、电、网”等多维情报,构成要素逐步健全,情报网络日益强健,整体能力有了长足的进步。但随着军事装备技术的发展,预警系统面临的目标环境愈发严峻,需通过挖掘系统内在机理,优化内部结构,强化系统能力。
“结构决定功能”是系统工程理论的基本认识。预警系统结构是预警系统的各组成要素即相互关系,决定了预警信息系统的形态、属性和功能,也是预警系统特性的标志和功能的载体。预警系统由众多实体以及其间复杂的连接关系构成的,基于复杂网络的战争系统建模方法可以将系统看成是由复杂节点所组成的,用复杂网络描述实体、实体间关系,以及相互作用的综合效果。在复杂网络运用到军事领域方面,CARES J 最先提出了利用复杂网络定量的描述了“分布式网络化战争”[1]。DEKKER 等介绍了一种基于智能体的仿真系统,用于研究网络拓扑对军事作战性能的影响[2]。国内李德毅等将复杂网络理论引入军事领域[3-5]。金伟新等探索了信息化战争作战体系拓扑网络的连接机制与分布规律[6]。张强等分析了作战体系的网络特性与形成机理,从静态隶属连接和动态交互出发建立了反映真实作战体系特性的网络描述模型[7]。王斌等把作战体系分为传感器、决策器、影响器和目标,用“作战环”衡量体系作战能力[8]。谭东风等采用随机格斗与Albert 网络“去点操作”,提出了统一表示交战行为与协作行为的网络随机格斗模型[9]。肖兵等构建了预警情报系统超网络模型,构建多种评估指标对系统能力进行了分析研究[10-12]。
综合分析现有文献,各位学者在将复杂网络理论运用到作战体系的过程中,均在拓扑结构的角度下去探讨建模问题,没有将空间概念纳入考虑范围。但在实际体系组建过程中,同一集团往往空间距离更近,连接关系也往往根据空间距离的远近划分,本文将空间属性与网络结构相结合,构建了更贴近实际的预警系统网络模型,并计算其静态能力。随后以该模型为基础进行动态仿真,在3 种毁伤条件下,采用不同的重连规则后分析预警系统作战效能的变化,给出系统结构优化建议。
1 预警系统特点及构成
1.1 预警系统概念和任务
预警系统是综合运用探测、侦察和监视手段及时发现并准确掌握来自陆、海、空、天、电、网等多维空间的威胁目标,为战略决策提供情报保障。预警系统的运作一般首先是根据任务组织各类探测资源获取探测的目标特征数据,然后通过对目标探测数据的融合、综合等处理形成决策所需的目标情报(敌情),指挥员再通过系统的决策支持功能对敌情我情进行综合分析与判断,形成一直的战场态势和制定作战方案,实现对隶属部队以及各类武器平台的指挥控制,隶属的部队及武器平台接收控制指令并采取相应的行动,整个流程不断往复,如图1 所示。预警系统的发展方向是通过对各类资源和功能的最优组织运用,一方面使得整个运作流程的节奏加快,整体效能提高,另一方面是充分发挥每类资源及其功能,获得系统的最大能力。
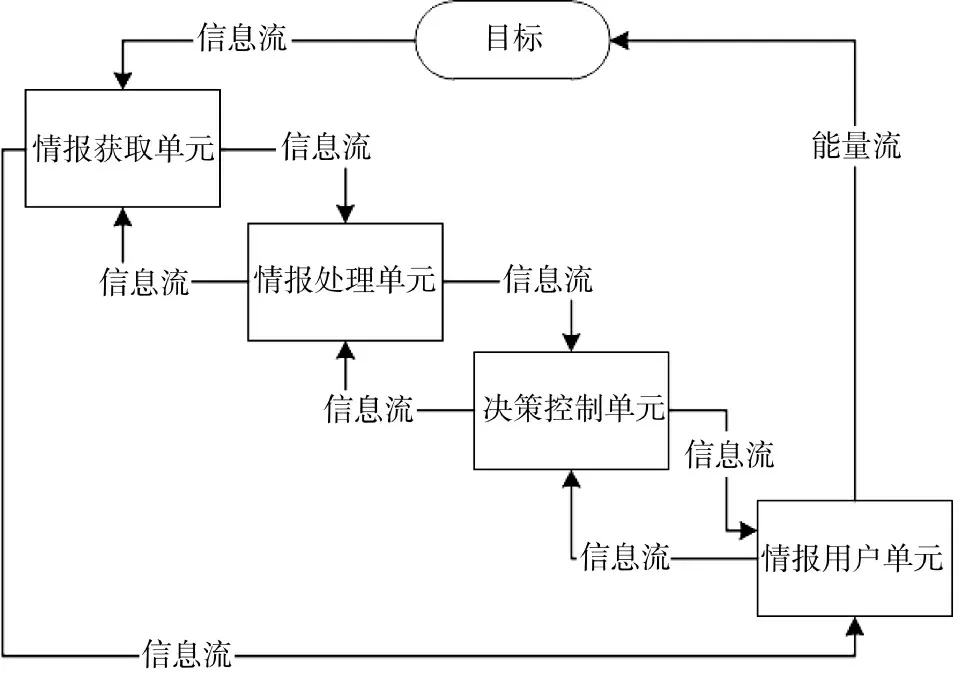
图1 预警系统任务流程图Fig.1 Flow chart of early warning system task
1.2 预警系统的实体构成
根据预警系统的一般运作流程,结合对大量已建的预警系统主要功能即组成要素的总结提炼与分析,可以将预警系统分为4 类基本功能,包括情报获取、情报处理、决策控制和情报用户功能。以系统的4 类基本功能为基础,初步将系统单元划分为4 类基本单元类型即情报获取单元(O,Observer),情报处理单元(P,Processor),决策控制单元(D,Decision)以及情报用户单元(A,Action),这4 类基本单元是对各级各类指挥信息系统主要功能本质特征的抽象与建模。下面分别对这4 类基本的系统单元的概念进行阐述。
1)情报获取单元
情报探测单元定义为一类具备战场探测和侦察能力的功能实体,利用电磁波的发射、接收收集整个战场的目标特征信息,是对各类侦察设备、系统的统称。
2)情报处理单元
情报处理单元定义为一类能够对战场目标情报进行综合处理的功能实体,即将多个情报探测单元捕获的情报信息经过综合处理,形成战场综合情报,支撑战场态势生成。
3)决策控制单元
决策控制单元定义为一类能够根据战场态势,形成作战方案并对隶属部队和武器平台(系统)实施统一指挥控制的功能实体。其主要根据情报综合分析结果,制定作战方案,下达作战命令。
4)情报执行单元
情报执行单元是一类能够根据决策单元的命令指示完成作战任务的功能实体,是对作战部队、各种武器平台以及火力单元等的统称。
5)连接关系
预警系统中存在着情报传输、指挥控制、信息协同等关系,这种两两交互的关系都可视为信息传输关系,可以运用连边的方式对其进行简化表示。根据单元的类型以及数量,综合现实情况考虑,可以将其分为6 类连接关系。传输方向和含义如表1所示。综合考虑各类单元以及连接关系后,形成的网络模型如图2 所示。

表1 预警系统连接关系类型Table 1 Type of connection relationship of early warning system
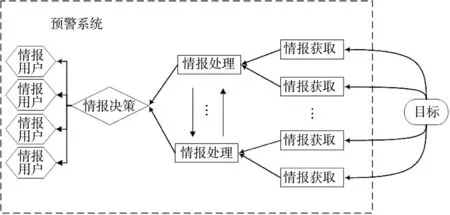
图2 预警系统网络模型概念图Fig.2 Concept diagram of early warning system network model
2 预警系统网络测度指标
目前,在系统的网络测度指标方面,一方面,部分专家学者运用复杂网络的基本参数对系统的结构属性进行判断。另一方面,为了使评判指标更符合实际,一般来说可分为系统效能指标和系统抗毁性指标,虽概念不同,但在实际评价中两者之间存在一定的关联关系,效能指标是抗毁性指标的基础,抗毁性指标由系统在对抗毁伤过程中的动态系统效能评判提供。在系统评价中,主要包括运用基于情报效能环的方法[11]、基于自然连通度的方法[15]、基于PEE 值的方法[16],综合对比基于情报效能环的方法更能体现预警系统特点,更具真实性,本文借鉴并改进情报效能环方法应用于预警系统。
2.1 预警系统网络化表述


2.2 预警系统网络分析指标
在复杂网络建模以及效能指标构建上,许多专家学者基于军事系统设计相关参数用以衡量系统中单元的重要性以及系统的整体效能性。本文通过对预警系统进行复杂网络建模后,一方面运用度和介数对单元重要性的排序,根据单元重要性由高到低的攻击方式,模拟实战中攻敌要害的战术手段。另一方面,借鉴谭跃进提出的根据体系中的完整作战链路数[14],判断体系能力,提出符合本模型的有效作战链路数评价指标,为验证多种重连方式的优劣提供评判依据。
1)单元的度分布:与一个单元连接的边的总数称为该单元的度,从直观角度来看,连接关系越多的单元,其重要性相对来说就越高。将网络中单元的度是否相同作为归类标准,对所有单元的度进行统计,得到的结果即为度分布。
2)单元介数:是指经过该单元的最短路径数。在系统中,有些单元的度虽然小,但是它很可能是两个集团的重要联络单元,如果去掉该单元,那么就会导致两个集团联系中断。因此,单元介数可以作为衡量系统动态抗毁特性的重要指标。单元介数的计算公式如下:
将单元介数进行归一化处理后公式为:
其中,npq是单元p 和q 之间的最短路径总数;npq(i)是连接单元p 和q 而且经过单元i 的最短路径数量。
3)平均路径长度:网络中任意两个单元之间距离的平均值。用来刻画系统中单元的分离程度,平均路径越短,系统中单元间的信息流动、共享和同步越高效迅速。计算公式如下:
其中,dij为i、j 两个单元最短路径所包含的边的条数。
4)有效作战链路数(number of combat line,NCL):系统从O—A 的路径长度一定的链路条数。John Boyd 认为,武装冲突可以看作敌对双方谁能更好地完成“观察—调整—决策—行动”的循环过程,即实现OODA 的完整循环。因此,作战过程中,拥有一条完整的OODA 链,即表示具备一套完整的作战能力。考虑到指挥关系的影响,从获取到执行可能经过多个中间单元,导致时延增长、情报失效,最终使得任务失败。因此,将中间单元控制在有限个数内,就能构成一条有效作战链,一个系统中NCL 的计算方式如下所示:
3 静态模型生成
一般来说可以通过基于数据、基于规则等方式对预警系统的模型进行实例化。基于数据生成需要有实战或者演习的前者可以根据可靠数据构建符合真实情况的网络结构。
3.1 静态模型构建算法
1)生成二维战场空间,战场大小为K×K。
2)设定网络规模,确定O、P、D、A 单元个数,将各单元随机落入战场空间内。
3)①部分邻近的O 单元有协同关系,则OO 单元之间的连接概率为POO,(di表示单元i 到目标点的距离,Dij表示单元i 到单元j 的距离;T 表示距离i 单元最近的前T 个单元,这些单元依概率与i 单元连接)。②根据预警信息情报流程,每一个O 单元一定与一个P 单元连接,连接概率POP依然受距离关系影响,算法与OO 连接相同。③个别关键的O 单元直接与将情报传递给D单元,也受到D 单元的直接指挥,设置OD 之间的连接概率POD。
4)所有的P 单元至少与一个D 单元连接,连接概率由单元之间的距离确定。由于隶属于同一D 单元的P 可以情报互联,因此,它们相互之间有连接关系。
5)考虑到指挥控制的和避免多重指挥造成的干扰,一个A 单元只与一个D 单元连接。又因为在A 单元与D 单元的连接中,空间距离不起决定性作用,所以A、D 之间采用随机的方式连接。
6)为方便观察,将O、P、D、A 4 类单元分为4层,其X,Y 坐标为他们在二维战场中的位置,纵坐标用作区分层次,无实际物理意义。
静态模型构建共构成OO,OP,PP,PD,DD,DA 6 个邻接矩阵,组合而成的系统整体邻接矩阵如式(5)所示。
其中,OA,PA,AA 之间不构成连接,其邻接矩阵为零矩阵。则最终形成的邻接矩阵为:
3.2 静态模型生成
在Matlab 2018b 软件平台上开展仿真实验,实验参数设置为:K=100,NO=60,NP=15,ND=8,NA=10,=10。将依照本文生成算法生成的基于距离的OO 协同连接图(如图3 所示)与O-O 协同随机连接图(如图4 所示)进行对比分析。
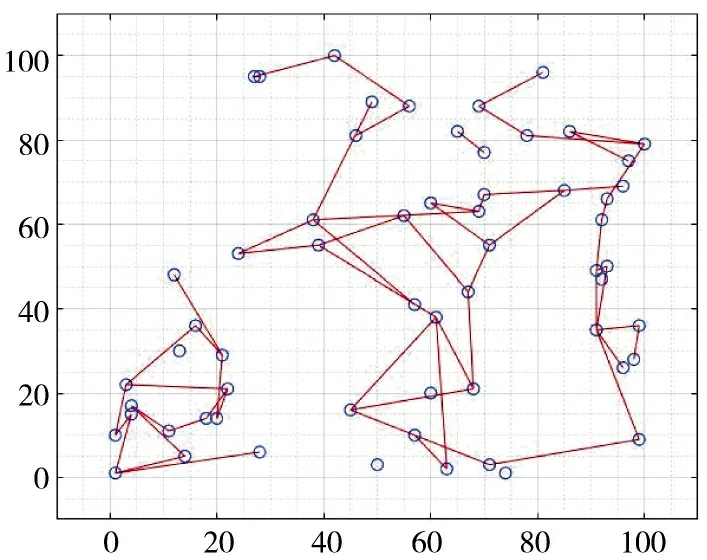
图3 基于距离的O-O 单元协同连接图Fig.3 O-O unit collaborative connection diagram based on distance
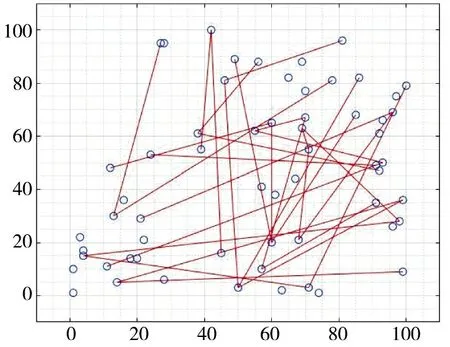
图4 O-O 单元协同随机连接图Fig.4 O-O unit cooperative random connection diagram
根据生成的连接图分析,基于距离的OO 协同连接图明显更符合实际,距离较近的情报获取单元之间具有协同关系的可能性更大;而随机OO 单元协同连接在空间距离上跨度大,若运用到实际中,必然会导致建设经费的增加以及协同效率的下降。同理,PD 单元连接同样如此,反映出了本算法将空间距离纳入考虑更贴合当前预警系统发展实际,生成的网络将更具真实性。
最终根据算法生成的基于欧式距离的网络图如图5、图6 所示。
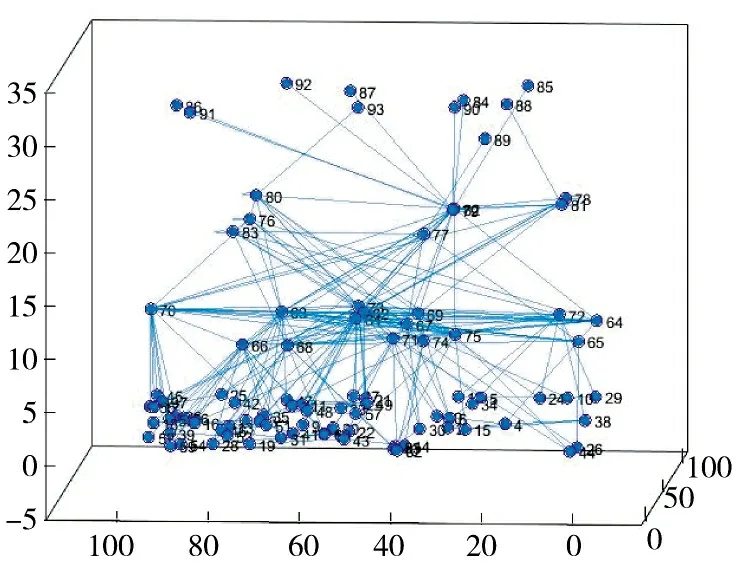
图5 预警系统三维静态结构模型图Fig.5 3D static structure model diagram of early warning system
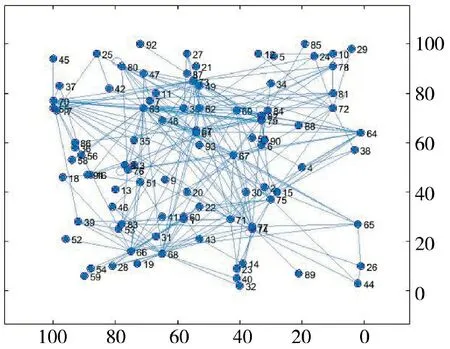
图6 预警系统二维静态结构图Fig.6 2D static structure diagram of early warning system
3.3 静态模型合理性分析
3.3.1 系统度与介数分析
图7、图8 为经过100 次重复实验后统计得出的度分布图以及单元介数分布图:

图7 度分布图Fig.7 Degree distribution diagram
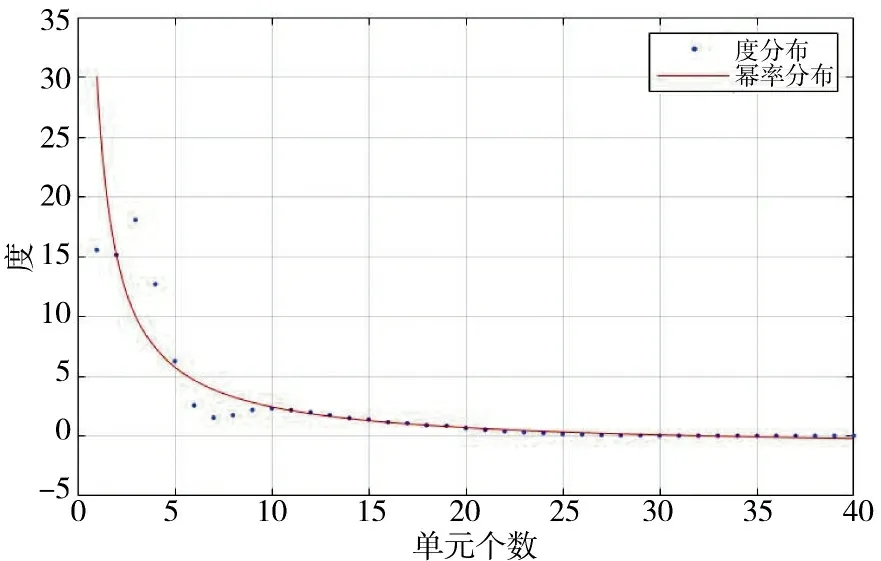
图8 幂率分布拟合图Fig.8 Power rate distribution fitting diagram
通过拟合图可以看出,本算法生成的预警系统单元的度分布近似于幂率分布,近似于符合无标度特性,反映到连接关系上就是少数指挥单元连接大量配属单元,符合军队系统指挥中枢为大脑、为核心这一特点。
图9 和图10 是实验100 次以后取得的均值结果,反映了系统中各单元自身介数和度的情况。P 单元的编号为61~75,D 单元的编号为76~83,在单元介数角度来看,从第P 单元开始有明显的跳变,到第A 单元骤降为0。从度的角度来看,每一类单元的度数趋于稳定,且着重向P、D 两类单元倾斜的趋势。表现出指挥机构重要性远高于基础装备单元这一特点,与实际情况相符,进一步验证了模型的真实性。
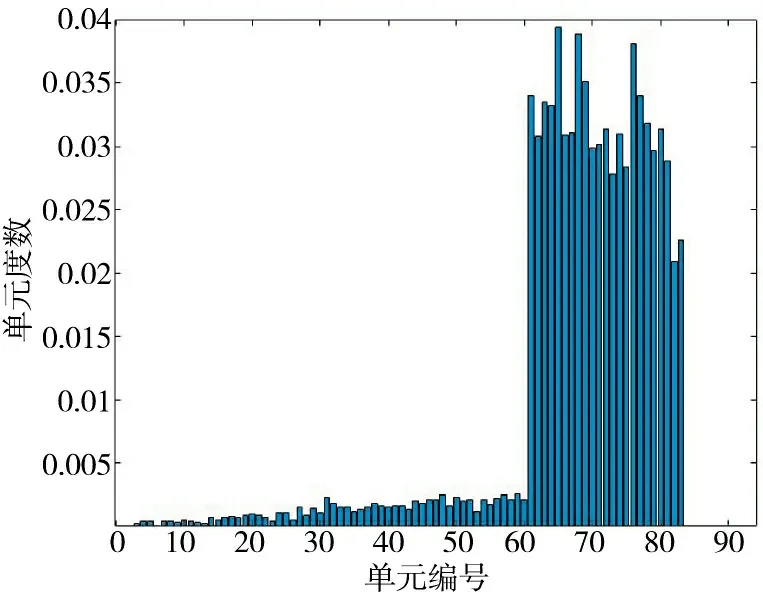
图9 单元介数分布图Fig.9 Unit betweenness number distribution diagram
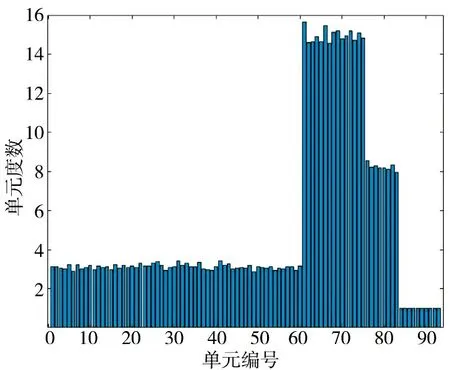
图10 单元度分布图Fig.10 Unit degree distribution diagram
3.3.2 系统平均最短路径分析
图11 为运用本文算法重复实验100 次(生成了100 次预警系统网络)后,系统平均最短路径结果图,可看出本算法在生成的系统网络最短路径的值较为稳定,也就是每次生成系统网络的性质差异不大,证实了本算法生成的预警系统具备良好的稳定性,在仿真过程中可运用蒙特卡洛实验法,提高仿真实验的准确性。
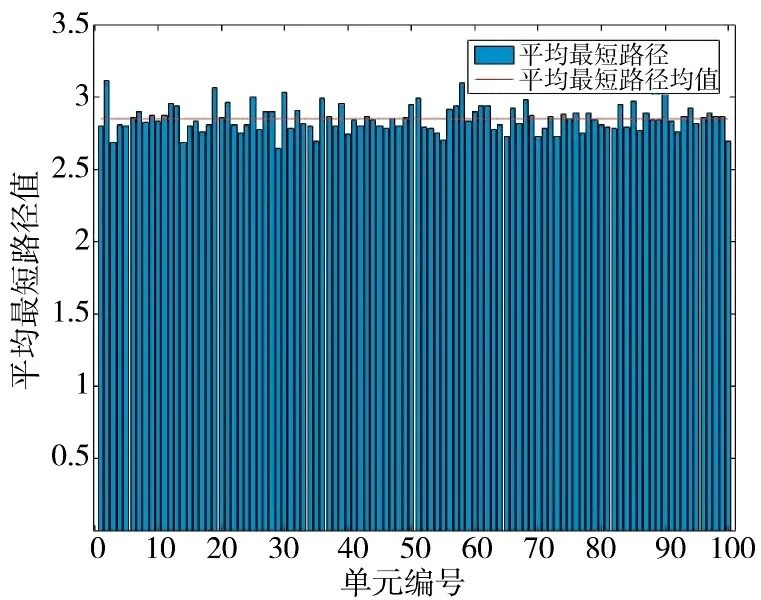
图11 平均最短路径数值图Fig.11 Average shortest path numerical diagram
4 模型的动态演化
4.1 网络动态毁伤
在系统毁伤上,采取随机摧毁和蓄意摧毁两种摧毁方式进行实验。随机摧毁实验指对于将要打击的系统处于黑盒状态,只能随机摧毁。蓄意摧毁指对于将要打击的系统视为白盒,用度和介数两种方式对单元重要性排序,并从大到小一次摧毁。虽然在摧毁重连过程中,系统结构发生了变化,此时的系统对于攻击方来说类似于灰盒状态,因此,在无法准确判定系统单元摧毁重连过程中单元重要度排序的情况下,仍然运用初始时的排序攻击,仍能较大程度的毁伤系统。
1)随机摧毁:在网络中随机寻找t 个单元,依次从系统中删除,观察NCL 指标的变化,通过多次实验的方式减少随机误差。
2)蓄意摧毁。①优先度摧毁:对系统中的单元按照度大小依次排序,选取排序靠前的t 个单元,依次从系统中删除,NCL 指标的变化。②优先介数摧毁:与优先度类似,选取介数靠前的t 个单元,依次摧毁并观察NCL 指标的变化。
同样为了消除随机造成的影响进行100 次重复实验,图12 为基于同一静态模型运用不同的单元摧毁方式NCL 指标的变化情况,其中,t=10,NCL中l=3、k=4。

图12 3 种摧毁方式下NCL 变化情况Fig.12 Change of NCL under three kinds of destruction modes
从NCL 变化情况可知,随机摧毁使系统NCL缓慢下降,蓄意摧毁对该系统有剧烈影响,符合系统破击战略追求的打击少数单元实现大面积毁伤的作战效果。
4.2 动态重连规则
1)当单元O 为孤立单元(与上级单元无连接)时,重新连接进入作战链路。①P 单元优先重连:在摧毁过程中,当O 点为孤立点时,优先与任意一个P单元进行连接。②D 单元优先重连:当O 点为孤立点时,优先与任意一个D 单元进行连接。③P、D 单元综合重连:当O 点为孤立点时,与任意P、D 单元进行连接。
现实意义:当指挥O 单元的上级单元被摧毁,O单元获取的目标情报无法得到应用,需要通过重新连接使情报得到有效利用,重新参与到作战环境中,且一般P、D 单元均具备一定的情报处理能力。因此,O 单元可以选择性向P、D 单元上报情报,使情报得到运用。
2)当单元P 无上级指挥单元D 时,与任意现存的上级指挥单元D 进行重连,进入作战链路。
现实意义:分两种情况考虑,一是P 综合下属O单元传递的情报并通过筛选处理形成优质情报,如无上级指挥单元D,则造成战场资源浪费,应该找到D 单元将情报运用到作战链路中;二是如P 单元成为一个孤立单元,可以与上级D 单元连接,作为一个冗余备份单元而存在,随时接替其他P 单元处理情报。
3)当单元D 孤立时,与任意友邻D 单元连接,进入作战链路。
现实意义:作为冗余备份单元随时接替其他D单元。
4)当A 单元孤立,与任意上级指挥单元D 连接。
现实意义:A 孤立将无法获取目标信息,从而无法实施准确打击,需要与上级指挥单元连接,获取准确情报信息完成最终打击任务。
4.3 实验方式
实验按照摧毁方式不同分为3 项实验,每一项实验又基于3 种不同的重连规则动态演化,其中,t=10,NCL 中l=3、k=4,每种实验重复100 次,尽可能消除随机误差,形成最终结果并分析。
4.3.1 随机摧毁重连
随机摧毁下的系统NCL 动态变化如图13 所示,由实验结果可知,系统的效能呈现有重连明显强于无重连,P、D 均能作为O 单元的连接点时,系统的整体效能下降最慢,表明在随机摧毁情况下,O单元在拥有更多的备选连接单元时,能使系统可以更好地保持其作战能力。
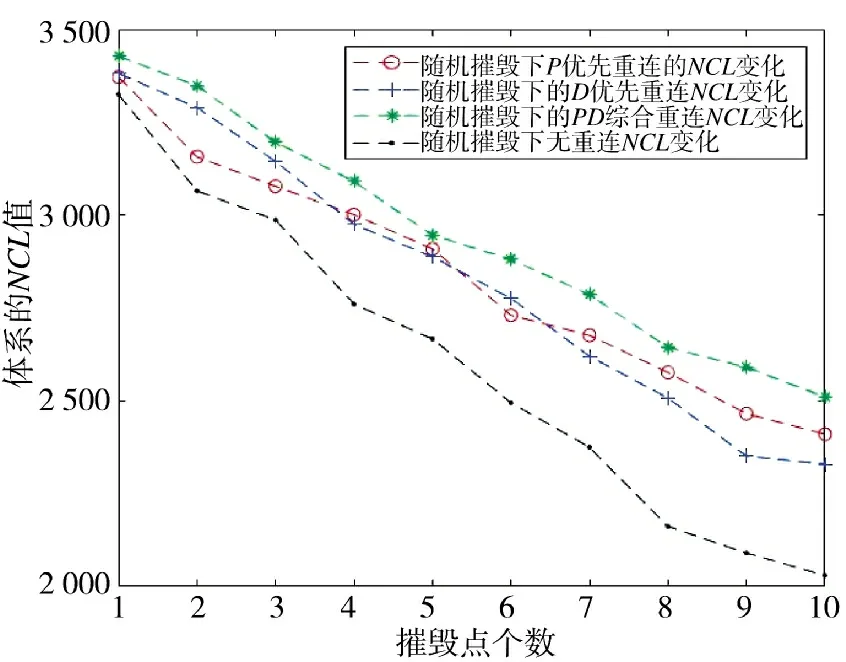
图13 随机摧毁下的系统NCL 动态变化Fig.13 NCL dynamic change of the system under random destruction
4.3.2 蓄意摧毁重连
基于度和基于介数摧毁下的系统NCL 动态变化如图14、图15 所示。根据实验结果分析,蓄意摧毁下的两种摧毁方式均显示出优先D重连比优先、PD 重连和优先P 重连有更好的抗毁效果。从实际作战情况分析,优先与D 单元连接,缩短了指挥层级,作战链路能流转更加迅速,因此,NCL 曲线在随着摧毁单元个数增加的过程中,甚至出现能力略微提升的现象。该实验结果用实际数据表明,预警系统采用扁平化的方式改进编制结构对于系统的抗毁能力和作战效能均有良好的改善效果。
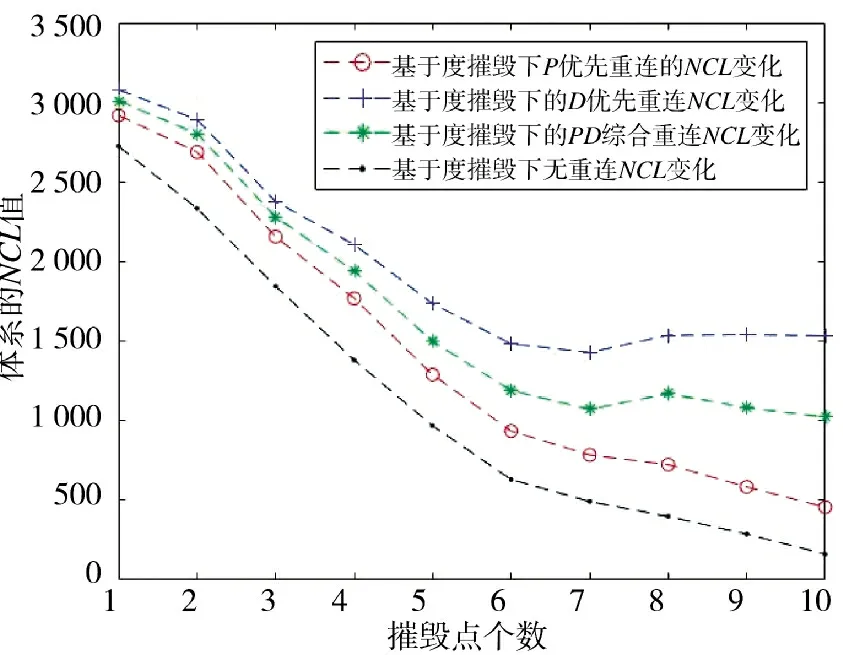
图14 基于度摧毁下的系统NCL 动态变化Fig.14 Dynamic change of system NCL based on degree destruction
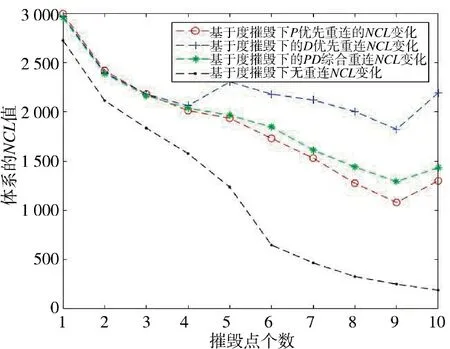
图15 基于介数摧毁下的系统NCL 动态变化Fig.15 Dynamic change of system NCL under betweenness-based destruction
5 结论
本文在总结复杂网络在作战系统建模与仿真研究现状的基础上,建立了预警系统复杂网络模型,通过仿真得到了一些有意义的结论。1)将空间距离纳入单元连接考虑,得出的预警系统网络模型更贴合实际。2)在受到随机攻击时,如孤立的O 单元运用P、D 单元综合重连,能使系统的作战能力得到更加有效的维持。3)在受到蓄意攻击时,在D 单元具有足够强的处理能力(可连接多个O 单元)的情况下,采用D 优先重连策略具有最好的抵御打击产生的效果,即缩短指挥链路,使指挥趋于扁平化有利于预警系统效能提升。

