基于PSO-BP 神经网络的高原寒地维修器材换算系数研究
王金帼,王亚彬,王 帅,乔智勇
(陆军工程大学石家庄校区,石家庄 050003)
0 引言
陆军装备维修器材(简称维修器材)是陆军装备维修所需的总成、零部件、元器件、附件,以及原材料、消耗材料等的统称[1]。维修器材是实施装备维修保障的重要物质基础,装备的使用和维修都需要大量的维修器材[2]。如果维修器材数量不足、种类不齐全,就不能及时修复战损装备,恢复战斗力。反之,过多的维修器材会造成经济浪费,占用宝贵的运输资源和储备资源,从而影响真正必要的器材供应。因此,科学、准确地对维修器材数量、种类的需求进行预测是装备保障的关键环节。
当前,需求预测的主要方法分为:定性预测方法[3],如专家会议法[4]和德尔菲法[5];定量预测方法[3]主要有指数平滑法[6]、季节性分析法[7]、线性回归法[8]等;智能预测方法有灰色预测法[9]、神经网络法[10]、支持向量机法[11]等。针对装备维修器材的需求预测,已经有诸多学者进行了研究。贺拥亮针对应急状态下军械备件需求依据经验判断导致预测不准的问题,分析影响备件需求的主要因素,运用神经网络模型进行预测[12]。刘畅等运用PSO算法优化极限学习机的权值和阈值,提高了网络稳定性[13]。杨帆等针对器材需求受不同任务的影响较大,对装备器材消耗影响因素进行分析研究[14]。
上述各种预测模型为器材需求预测提供了借鉴。高原寒地地域环境特殊,作战任务特殊,军械装备维修器材需求更为复杂,呈现出非线性等复杂特性,沿用平原地区通用方法很难做到准确预测。同时,特殊的地域环境对维修器材中电子件、机械件、橡胶件需求规律影响差异较大,需分别进行研究。结合PSO 全局搜索能力强、收敛速度快和BP 神经网络对任意非线性函数很好的拟合能力,本文提出一种基于PSO-BP 神经网络的维修器材换算系数模型。通过对器材需求影响因素进行全面分析,确定不同影响因素的描述性变量并将其量化作为输入变量,将电子件、机械件、橡胶件这三类军械装备维修器材的换算系数作为输出变量,研究了高原寒地军械装备维修器材需求预测方法。通过算例验证了该方法的可行性和准确性。
1 高原寒地军械装备维修器材需求影响因素分析
高原寒地部队为保证国家主权和领土完整,担负着重要的军事训练任务和作战任务。在实际作战过程中,各种因素都会对维修器材需求产生影响,从而导致故障率更加复杂。维修器材中的电子件、机械件、橡胶件在不同的环境变化下,产生各自不同的规律变化,分别研究其规律特点可以对不同种类的维修器材进行更为准确的预测。其中,电子件、机械件、橡胶件分别对海拔、风沙、温度的影响较为敏感,因此,应区分这三类维修器材并对其进行研究。
1.1 高原寒地主要特点
高原寒地作战的主战场平均海拔4 000 m 以上,一是受高原寒地特殊环境的影响,自然环境恶劣,主要表现在:海拔高、空气含氧量低,温度低、温差大,风力大、沙尘多。二是高原山地的特点更加明显,山地面积占75%以上,地形险要,山高坡陡,沟谷纵横,达坂地形多,道路质量差。三是高原寒地社会环境较为复杂,主要包括历史环境、宗教环境、经济环境的影响。历史上高原寒地战争频发,导致发生战事概率较大;同时受境外环境影响冲击,宗教复杂;由于交通环境较差,地广人稀,在经济发展上也存在一定差异。
由于高原寒地呈现出诸多特点,导致对军械装备维修器材需求影响较大,规律特点与标准情况不同,需要针对以上特点进行相关研究。
1.2 影响因素分析
依据高原寒地地域特点,从作战规模、作战环境、装备情况、人员情况、保障构想5 个方面对维修器材需求影响因素进行分析。
1.2.1 作战规模
作战规模的影响主要包括作战任务、作战样式、作战强度和作战持续时间4 个指标。
1)作战任务。依据国家战略、历史和外交因素,按照任务和规模,通常分为战略任务、战役任务和战术任务。
2)作战样式。按照敌情、地形、兵力等不同情况,可分为不同的样式,通常的样式有进攻战斗、防御战斗、威慑等。
3)作战强度。根据作战的激烈程度,可以将作战强度分为高强度作战、中强度作战和低强度作战。
4)作战持续时间。从战争开始到战争结束整个过程将持续进行的时间。
1.2.2 作战环境
作战环境主要考虑地形地貌、气候环境和社会环境的影响。
1)地形环境。指的是地表各种各样的形态,作战地域地形主要是高原。
2)气候环境。指作战地域气候的平均状况,主要要素有海拔、温度、风沙等。
3)社会环境。主要包含有历史、宗教、经济等因素的影响。
1.2.3 装备情况
装备情况主要包括装备数量和装备可靠性的影响。
1)装备数量。是指所有参加战斗的装备总数。
2)装备可靠性。是指装备在规定条件下和规定时间内完成规定功能的能力,可用故障率来衡量。故障率越小,可靠性越高,所需的维修器材越少。
1.2.4 人员情况
主要考虑人员的综合素质和对装备的操作水平两个方面。
1)综合素质。高原寒地下恶劣的气候环境以及残酷的战争对人员身体和心理素质都会有很大影响,综合素质高的人员战斗力强,可以较好地操作使用武器装备,对器材需求相对较少。
2)操作水平。操作水平的高低对装备的正常运行影响很大,操作技能越好,对装备损坏越少,所需维修器材越少。
1.2.5 保障构想
保障构想是指根据作战实际情况,决定最终进行维修器材保障的效果,战时装备修理以换件修复为主,旨在形成提高装备完好率、修复率的重要保证。主要采用器材保障率、平均保障时间、保障费用等指标来衡量。
1)器材保障率是指装备被保障的程度。保障率越高,保障效果越好,就需要越多的维修器材。
2)平均保障时间是指完成保障任务所需的时间。
3)保障费用是指完成保障任务所需的费用。
维修器材需求影响因素如图1 所示。

图1 维修器材需求主要影响因素Fig.1 Main influencing factors of maintenance equipment demand
1.3 影响因素量化处理
由图1 可知,将影响因素分为5 个主要方面的基础上,又进一步具体细化,共18 个相关变量,分别为作战任务x11、作战样式x12、作战强度x13、作战持续时间x14、地形环境x21、海拔x221、温度x222、风沙x223、历史x231、宗教x232、经济x233、装备数量x31、装备可靠性x32、综合素质x41、操作水平x42、器材保障率x51、平均保障时间x52、保障费用x53。通过分析,可以将18 个变量分为定性变量和定量变量,分别对定性变量进行量化处理和对定量变量进行描述分析。
1.3.1 定性变量量化
定性变量为作战任务x11、作战样式x12、地形环境x21、历史x231、宗教x232、经济x233、综合素质x41、操作水平x42。以上变量可以采取邀请不同专家进行评判,基于专家经验法进行打分,确定其数值,具体结果如表1 所示。
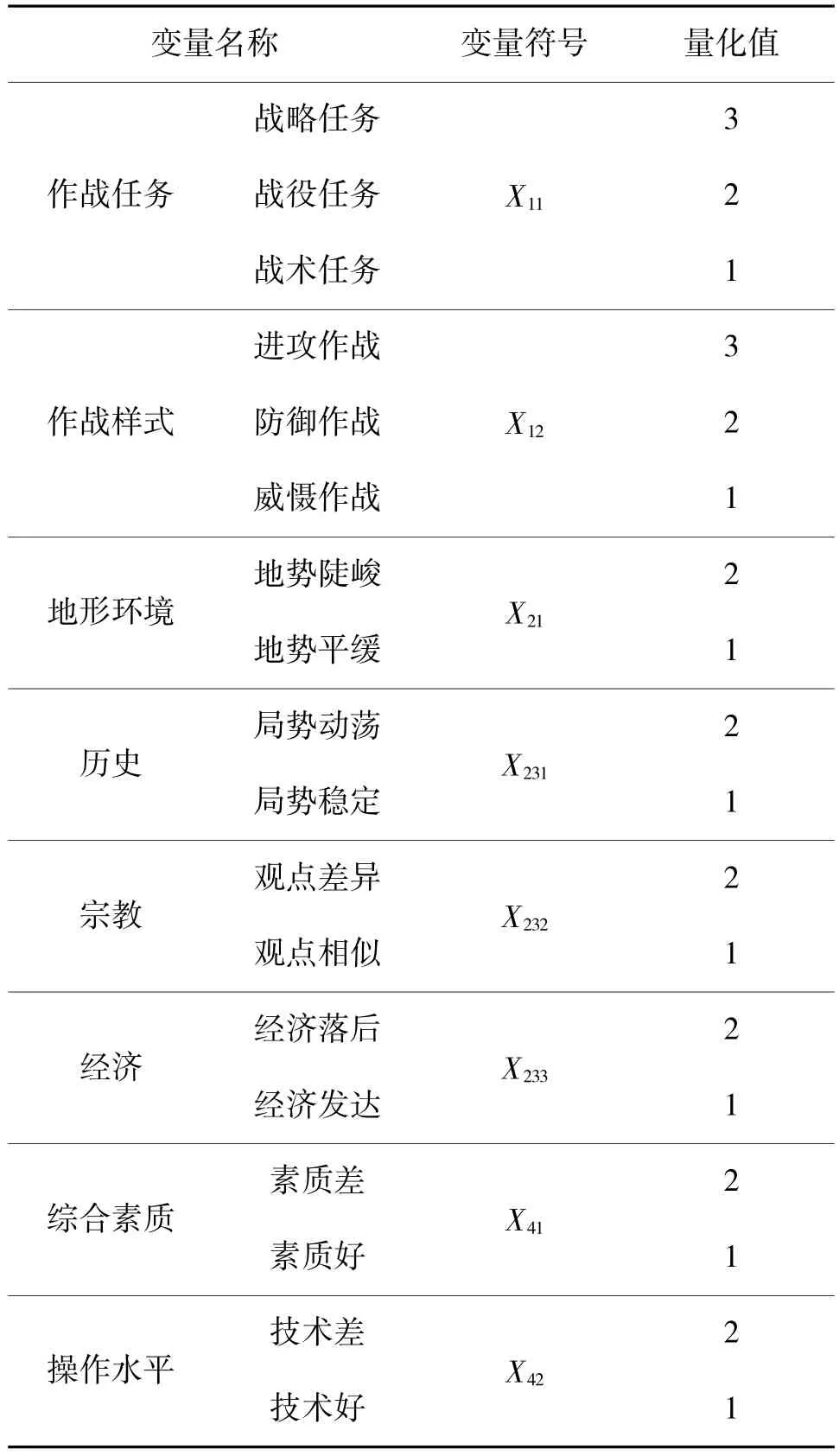
表1 定性变量量化Table 1 Quantification of qualitative variables
1.3.2 定量变量描述
定量变量为作战强度x13、作战持续时间x14、海拔x221、温度x222、风沙x223、装备数量x31、装备可靠性x32、器材保障率x51、平均保障时间x52、保障费用x53。
1)作战强度x13:x13=T2/T1
式中,T2为战时平均每天计划使用时间(单位:h/d);T1为平时平均每天计划使用时间(单位:h/d)。
2)作战持续时间x14:是指整个作战过程持续的时间,单位为h。
3)海拔x221:是指作战地域的平均海拔高度,单位为m。海拔每增高1 000 m,大气压降低12%,外绝缘强度和电晕电压降低8%~13%,电子件故障率增高。
4)温度x222:是指作战地域在作战时间内的平均温度,单位为℃。随着温度的降低,橡胶件的机械性能下降,-30℃下橡胶件容易折断、剥裂。
5)风沙x223:可用平均风力的大小表示,划分为0~18 个等级。风力越大,大气中污染物扩散越快,沙尘沉积越多,机械件磨损越严重,损坏率越高。
6)装备数量x31:是指参加战斗的装备总数,单位为件。
7)装备可靠性x32:可用装备故障率来衡量。是指装备工作到时刻t 还没发生故障,那么该装备在以后单位时间内发生的故障概率,即装备故障率。
8)器材保障率x51:器材保障率P 是指装备在规定条件下,在任意随机时刻一旦需要器材有所需器材的概率。
9)平均保障时间x52:是指完成保障任务所需的时间,单位为h。
10)保障费用x53:是指完成保障任务所需的费用,单位为元。
1.4 变量归一化
1.4.1 直线型归一化
将变量作战任务x11、作战样式x12、地形环境x21、历史x231、宗教x232、经济x233、综合素质x41、操作水平x42、作战强度x3,采用极值法进行归一化,如式(1)所示。
1.4.2 曲线型归一化
将变量作战持续时间x14、海拔x221、温度x222、风沙x223、装备数量x31、装备可靠性x32、器材保障率x51、平均保障时间x52、保障费用x53,采用升半Γ 型公式,如式(2)进行归一化,如图2 所示。
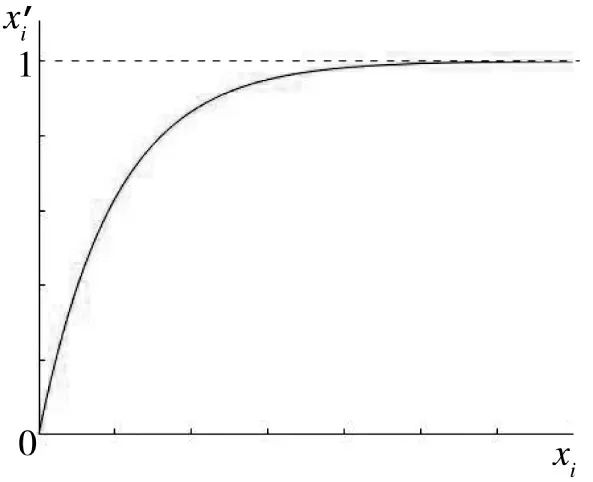
图2 升半Γ 型图Fig.2 Ascending half Γ type diagram
式中,k 为调节系数。
2 基于PSO-BP 神经网络的维修器材需求预测模型构建
2.1 基本概念
2.1.1 BP 神经网络概述
BP(back propagation)神经网络是1986 年由Rumelhart 和McClelland 的科学家提出的概念,是一种按照误差逆向传播算法训练的多层前馈神经网络,是应用最广泛的神经网络模型之一[15]。BP 神经网络有3 层:输入层、隐含层和输出层,各层之间实行全连接。实际运用中常采用3 层神经网络,其网络结构如图3 所示。
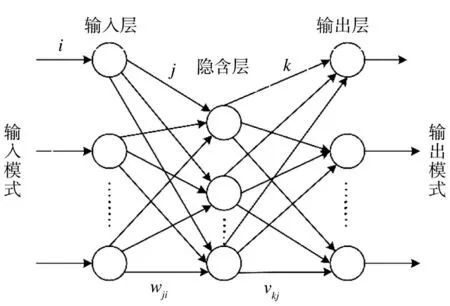
图3 3 层网络结构Fig.3 Sketch of 3-layer network structure
但由于其存在局部极小化、收敛速度慢、网络性能差、不稳定等缺点,因此,往往采用智能算法对BP 神经网络进行优化,利用智能算法在解析空间找到较好的搜索空间,再用BP 神经网络在较小的搜索空间寻求最优解[16]。
2.1.2 粒子群优化算法
粒子群优化算法(psrticle swarm optomozation,PSO)是由Eberhart 和Kennedy 在研究鸟类和鱼类的群体行为基础上于1995 年提出的一种群智能算法[17]。这种算法的全局搜索能力强,收敛速度快,能够快速收敛到局部最优值的范围内,因此,通常用粒子群优化算法来优化神经网络的连接权重和阈值。
2.2 基本原理
PSO-BP 神经网络算法是利用粒子群优化算法的全局搜索能力,来优化神经网络的拓扑结构、连接权值和阈值,将粒子群算法良好的全局寻优能力与BP 算法良好的局部寻优能力相结合,以提高神经网络的泛化能力和学习能力,从而改进神经网络的整体搜索效率。
2.3 算法实现
2.3.1 BP 算法的权值和阈值修正公式
式中,Hj为隐含层单元j 的输出;Ii为输入层单元i 的输入;vkj为从隐含层单元j 到输出层单元k 的连接权重;wji为从输入层单元i 到隐含层单元j 的连接权重;γk为输出层单元k 的阈值;θj为隐含层单元j 的阈值;η 为学习率,取值为(0,1);δk为输出层单元k的误差;σj为隐含层单元j 的误差;计算公式为:
式中,Tk为样本在输出层单元k 的目标输出;Ok为输出层单元k 的输出;Hj为隐含层单元j 的输出。
2.3.2 PSO 算法速度和位置更新公式
式中,i=1,2,…,n;n 是此群中粒子的总数;vi是粒子的速度;rand()是介于(0,1)之间的随机数;xi是粒子的当前位置;c1、c2是学习因子,通常c1=c2=2;vi的最大值为vmax(大于0),如果vi大于vmax,则vi=vmax;pbesti是个体粒子经过的最佳位置;gbesti是群体粒子经过的最佳位置。
式中,w 为惯性因子,其值为非负。w 的引入,可以使粒子获得更好的寻优结果。目前采用较多的时线性递减权值策略,如下:
式中,Gk是最大迭代次数;wini是初始惯性权值,典型取值为0.9;wend是迭代至最大进化代数时的惯性权值,典型取值为0.4。
2.3.3 PSO-BP 算法结合
通过PSO 算法不断更新粒子群的速度和位置,得到全局最优权值和阈值,运用于相应的BP 神经网络结构。定义粒子适应度函数为:
式中,n 为样本的数量;Ti为样本的目标输出;Oi为样本的实际输出。
个体极值更新公式为:
全局极值更新公式为:
上述算法流程可用如图4 所示。
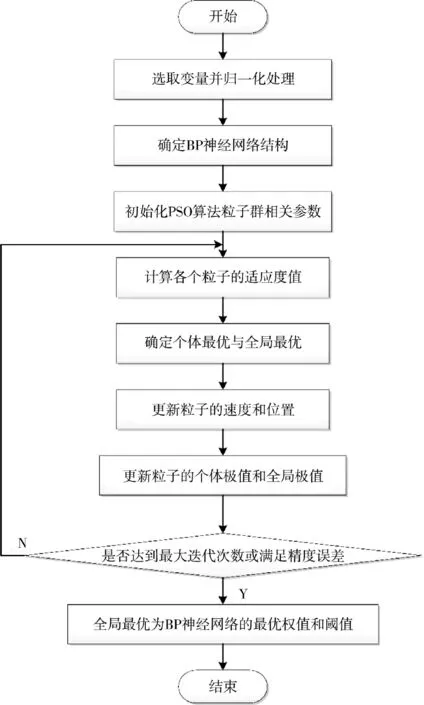
图4 PSO-BP 神经网络算法流程图Fig.4 Flow chart of PSO-BP neural network algorithm
3 算例分析
本文研究数据来自部队训练和完成任务的采集数据和不同地区的调查结果,选取近几次实战演习任务等实例数据,通过对维修器材影响因素分析,以18 个主要影响因素作为输入变量,输出为电子件y1、机械件y2、橡胶件y3这三类维修器材需求量的换算系数。而后结合18 个主要影响因素对PSO-BP 神经网络进行学习训练,学习样本如下页表2 所示。
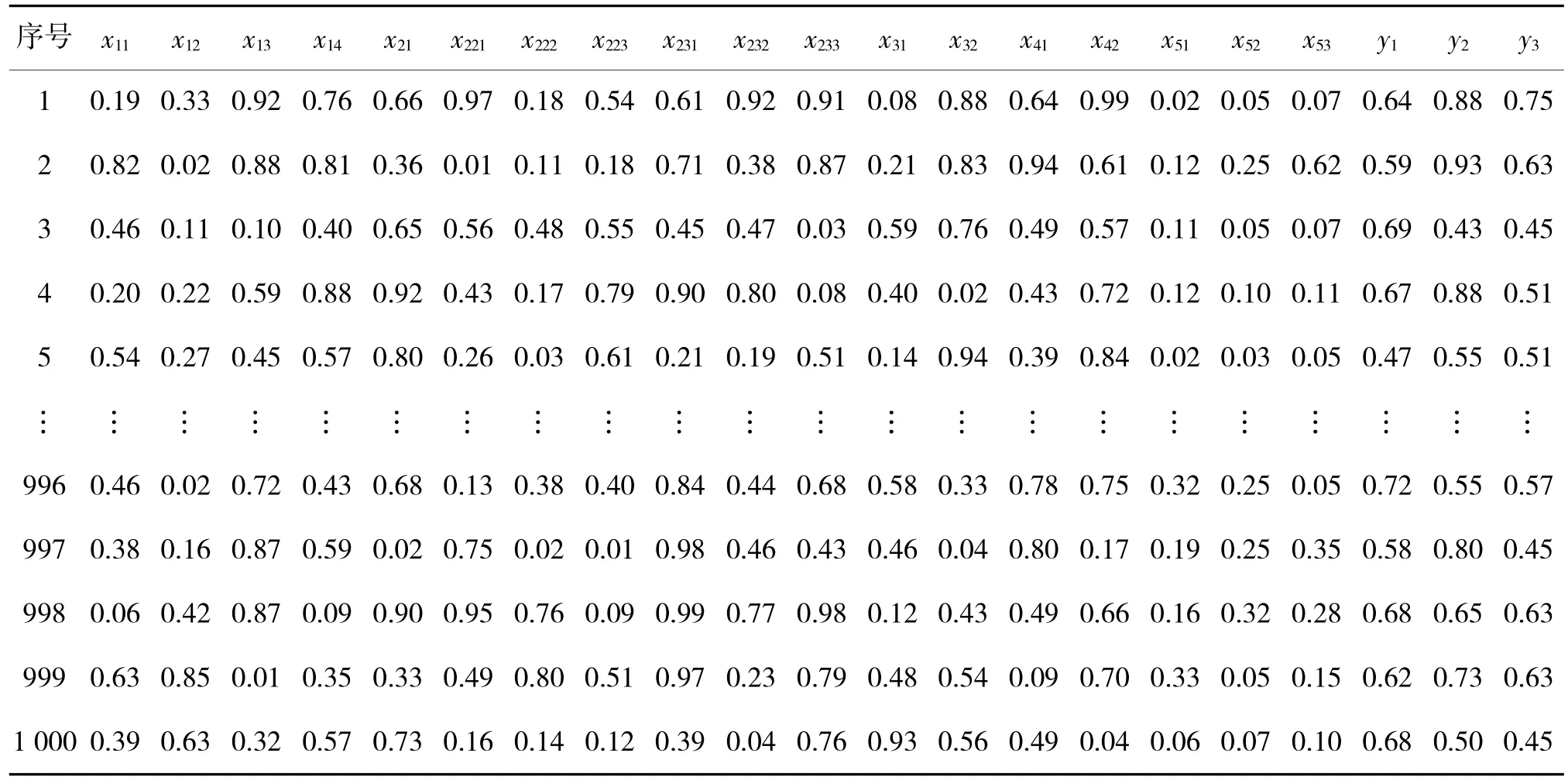
表2 PSO-BP 神经网络学习样本Table 2 Learning samples of PSO-BP neural network
运用PSO-BP 神经网络模型对维修器材需求换算系数进行预测,选取1 000 组样本数据运用PSOBP 神经网络模型对维修器材需求量换算系数进行学习训练,设置学习速率为0.1,学习次数为20 000,结果如图5 所示。
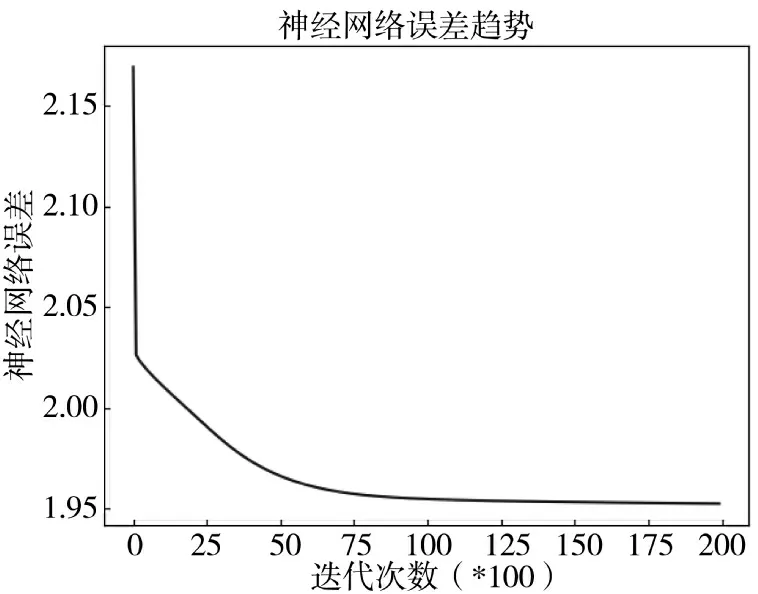
图5 维修器材换算系数误差变化曲线Fig.5 Conversion coefficient error variation curve of maintenance equipment
运用训练好的PSO-BP 神经网络,将表3 中的样本输入进行验证,得到维修器材需求换算系数的预测值,如表4 所示。

表3 PSO-BP 神经网络验证样本Table 3 Validation sample of PSO-BP neural network

表4 实际值与预测值对比Table 4 Comparison of actual and predicted values
通过对比表4 中实际值与预测值,可以发现误差在合理的范围之内,PSO-BP 神经网络模型可以较好地对维修器材进行需求预测,具有可行性和参考性。
4 结论
本文通过对高原寒地军械装备维修器材需求影响因素的分析,结合专家经验法对其量化并归一化处理,针对特殊的气候环境对不同种类器材影响的差别,构建基于PSO-BP 神经网络的维修器材换算系数预测模型,分别得出电子件、机械件、橡胶件这三类维修器材的换算系数。PSO-BP 神经网络的维修器材换算系数模型适用于具有一定实际数据的装备维修器材需求预测,仿真结果表明,采用PSO-BP 神经网络进行维修器材需求预测较为准确,对高原寒地维修器材保障具有重要的指导意义。

