基于深度学习的网络攻击检测模型*
禹 宁,谷 良,狄 婷
(国网山西省电力公司信息通信分公司,太原 030000)
0 引言
网络已经成为能源、金融、政务等国家基础设施和公民个人信息传输的主要载体,由于网络架构的开放性和其难以根除的系统漏洞,各类网络攻击层出不穷,尤其高级持续威胁(advanced persistent threat,APT)攻击已经成为近年来威胁我国网络设施安全的主要攻击形式[1],及时检测复杂多变的网络攻击,保障国家重要网络基础设施和公民信息安全成为目前网络安全研究的紧迫需求。
网络攻击通常主要有4 种形式,分别是DoS(Deny of Service)、Probe、U2R(User to Root)和R2L(Remote to Local),上述攻击形式也是APT 攻击过程中据点建立和横向移动阶段的主要攻击形式;一旦攻击达成便可长期驻留用户网络,适时窃取目标用户敏感数据信息,造成难以察觉的巨大破坏。针对上述攻击,目前存在大量研究。YANG Y Q 等针对U2R 和R2L 攻击提出基于改进密度峰值算法和深度置信网络的MDPCA-DBN 算法实现攻击检测[2],该算法针对良性数据的识别准确率达到97.38%,对于U2R 和R2L 的识别率分别达到6.5%和17.25%。CHUAN Y 等针对DoS 攻击提出基于CNN 和RNN的集成检测算法,识别率达到99.1%,但该方法计算开销较大[3]。SONG C H 等将网络攻击视为恶意流量,基于分类思想利用LSTM 和XGBoost 集成算法实现了恶意流量分类识别,但该检测方法检测精度较低[4]。刘海波等针对APT 攻击利用对抗网络提出了基于GAN-LSTM 的检测方法,实验表明融入生成对抗网络的检测算法对比LSTM 网络检测效果有明显提升[5]。针对DDoS 攻击,ROBSON V 等提出基于快速分层深度卷积神经网络的入侵检测算法(Tree-CNN)[6],并在模型顶层使用SRS 激活函数使模型具有更好的泛化能力和学习速度,该模型识别率达到97%,但该方法模型检测精度较低。YU J 等提出一种基于多尺度卷积神经网络(MSCNN)的高精度入侵检测系统[7],通过不同尺度的卷积核特征提取有效提升了卷积检测精度,针对上述各类攻击的平均准确率提高了4.37%。WU 等提出了LuNet模型[8],该模型针对Probe,DoS 攻击的检测率达到99%,但是对于U2R 和R2L 的识别率较低;IM RANA Y 等提出了基于双向长短期记忆网络的检测模型(Bi-LSTM)[9],该模型检测精度达到92.81%,但时间复杂度较高,训练时间达到9 789 s;高忠石等提出了基于主成分分析优化的长短时记忆网络的入侵检测模型(PCA-LSTM)实现二元分类,但该方法检测精度达到94.34%[10]。
针对网络复杂混沌特性导致的检测精度低、特征学习不充分、时间开销大等问题,本文提出基于深度学习的网络攻击检测框架GP-CABL,主要贡献包括:1)提出一种基于贪心策略与主成分相结合的GPCA(Greedy PCA,简称GPCA)方法,对网络流量的高维特征进行最优特征子集提取以降低模型时间复杂度;2)构建CABL 框架实现网络攻击检测:利用卷积神经网络(convolutional neural networks,CNN)和长短期记忆网络(bidirectional long short-term memory network,Bi-LSTM)充分提取流量的空间特征和时序特征,并基于注意力机制(attention)对学习过的特征图进行信息增强,以保证检测精度的同时加快模型收敛速度;3)通过充分实验验证和对比了GP-CABL 的有效性。
1 GP-CABL 网络攻击检测框架
1.1 网络攻击检测框架设计
GP-CABL 检测框架总体上是一个层次模型,检测流程如图1 所示,由特征构建层、数据预处理层、特征提取层、模型训练与测试层和结果输出层共5层构成。主要工作模式为:1)采集网络流量,并构建流量初始特征;2)对初始特征进行预处理;3)基于GPCA 提取初始特征的最优子集,并按照4∶1 比例构建模型训练集和测试集;4)训练CABL 模型;5)采用测试集进行模型评估,输出测试结果。
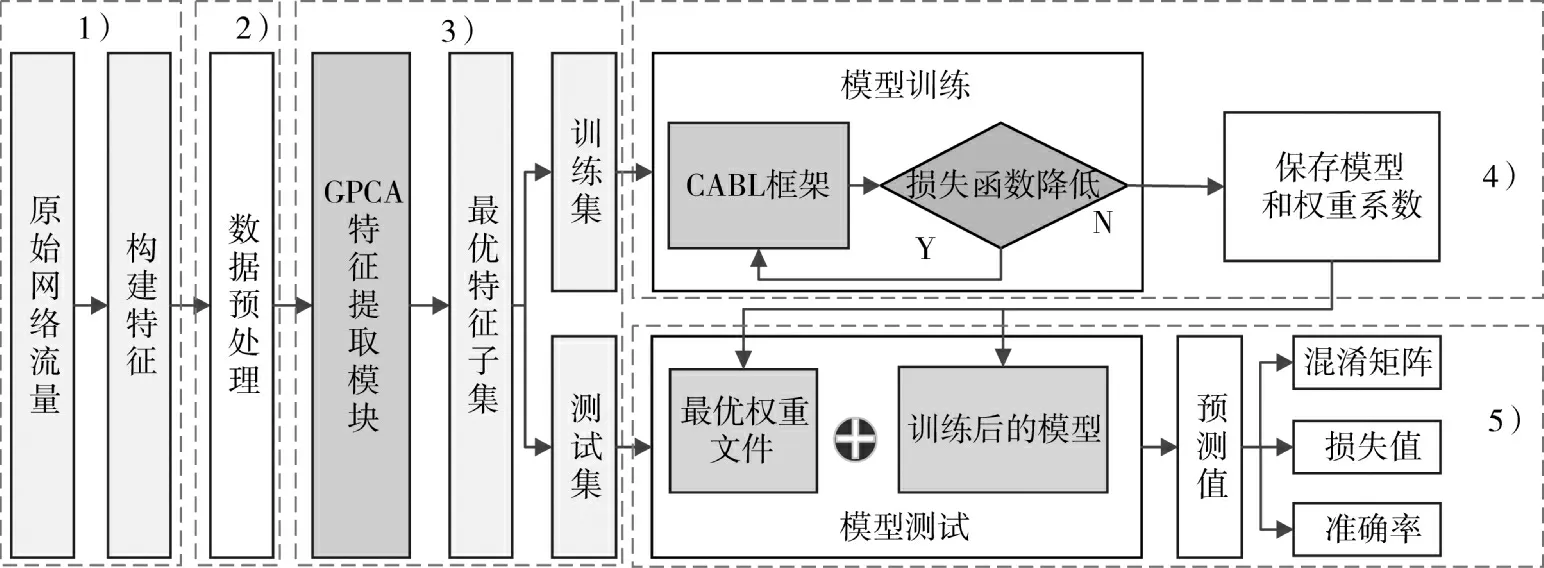
图1 GP-CABL 网络入侵检测流程图Fig.1 The flow chart of GP-CABL network intrusion detection
1.2 GPCA 特征提取算法
在恶意流量检测中,初始特征中包含的流量特征噪声多、维度高、冗余度大,是影响模型识别精度和性能主要因素,且初始流量特征对恶意流量检测贡献度并不均衡,因而挖掘关键流量特征成为降低模型复杂度、减少训练开销,提升模型鲁棒性的一个主要途径。PCA 算法能够对特征进行线性组合和归并,在保持流量主要信息量的情况下降低特征维度;贪心算法能够在训练参数保持最优的基础上对当前特征作出最优选择,基于上述分析,本文提出一种基于贪心与主成分相结合的GPCA 特征提取算法用于对初始特征进行降维,其实现原理及步骤如下所示。
设经过数据预处理后的初始特征集为S,且其共包含N 个对象,即,每个对象包含m 个变量,即:,其中,。
Step 1:求每个对象特征的平均值,即利用式(1)求出m 个特征的平均值,其中,表示第t 个特征的平均值。
Step 2:求Xi中每一维特征的相关系数矩阵R,即利用式(2)~式(4)求相关系数矩阵R。
其中,E(Xi·Xj)表示求向量Xi·Xj的期望,其计算方式如式(4)所示。
Step 3:提取低维度协方差矩阵Rk(k<m)。列出矩阵R 的每个列向量的2-范数,选择较大的k 列构成子矩阵Ck。2-范数的计算公式如式(5)。


Step 6:基于贪心策略选择模型学习率、迭代次数、模型隐藏层结点个数最优值,在上述参数保持最优的条件下,通过观察不同主因子k 对应的实验准确率变化趋势,寻找最优k 值。最终将数据S 集

由上述推理可知传统PCA 分解过程中,奇异值分解是其中计算复杂度最高也是计算开销最大的过程,在奇异值分解前针对特征降维是降低其复杂度的有效途径。GPCA 通过在奇异值分解之前对矩阵R 进行降维,有效减少了计算开销。从时间复杂度分析角度看,传统PCA 奇异值分解协方差矩阵的时间复杂度为O(N×m3),其中,N 为样本数量,m 是样本特征的数量。而GPCA 分解前首先将m 缩小至k(k<m),其时间复杂度为O(N×m3),当样本数量有限时,其计算开销明显降低,因此,GPCA 较传统PCA 能有效提升特征提取的速度。
1.3 CABL 恶意流量检测框架
CABL 恶意流量检测框架由流量空间特征学习、特征增强和时序特征学习模块3 部分构成,结构如下页图2 所示。从网络流量数据传输形式看,流量数据自上而下由报文、数据报、数据包、帧和比特构成,呈现显著的层次结构特征即空间结构特征;从流量采集的时间过程看,流量是严格按时间不断汇聚而成,是按照时间先后顺序构成的数据列,即网络流量数据是按照一定的时间粒度进行聚合构建的时序数据,具有鲜明的时序特征。网络流量在空间结构特征方面与自然语言呈现出显著的相关性,一维CNN 在自然语言处理领域取得良好的进展[11],CABL 借助CNN 特性,设置两层卷积层对GPCA 提取的最优特征子集进行学习和特征提取,通过设置两层最大池化层获取网络流量显著特征,得到新的特征图。针对池化层特征重构带来的信息损失问题,采用Attention 机制[12]对获取的显著特征进行增强,即通过为新获取的特征图中各特征赋予不同的权重来加速损失函数最小化。针对网络流量的时序特征学习,LSTM 网络利用细胞状态信息、输入门、遗忘门和输出门,有效地解决了梯度爆炸和梯度消失的问题,Bi-LSTM 网络利用正向LSTM 和反向LSTM 网络,兼顾历史和未来信息对当前状态的影响,能够充分地学习网络攻击发生时网络流量前后突变引起的时序特征变化,因此,CABL 借助Bi-LSTM[13]学习网络流量数据的时序特征。在模型训练中,利用基于贪心策略的调参方法寻找学习率、隐藏层神经节点个数、批处理大小等变量的参数,直到损失函数基本收敛后,利用检测率和准确率等模型评价指标获取模型最优参数;并利用测试集对CABL 进行验证。
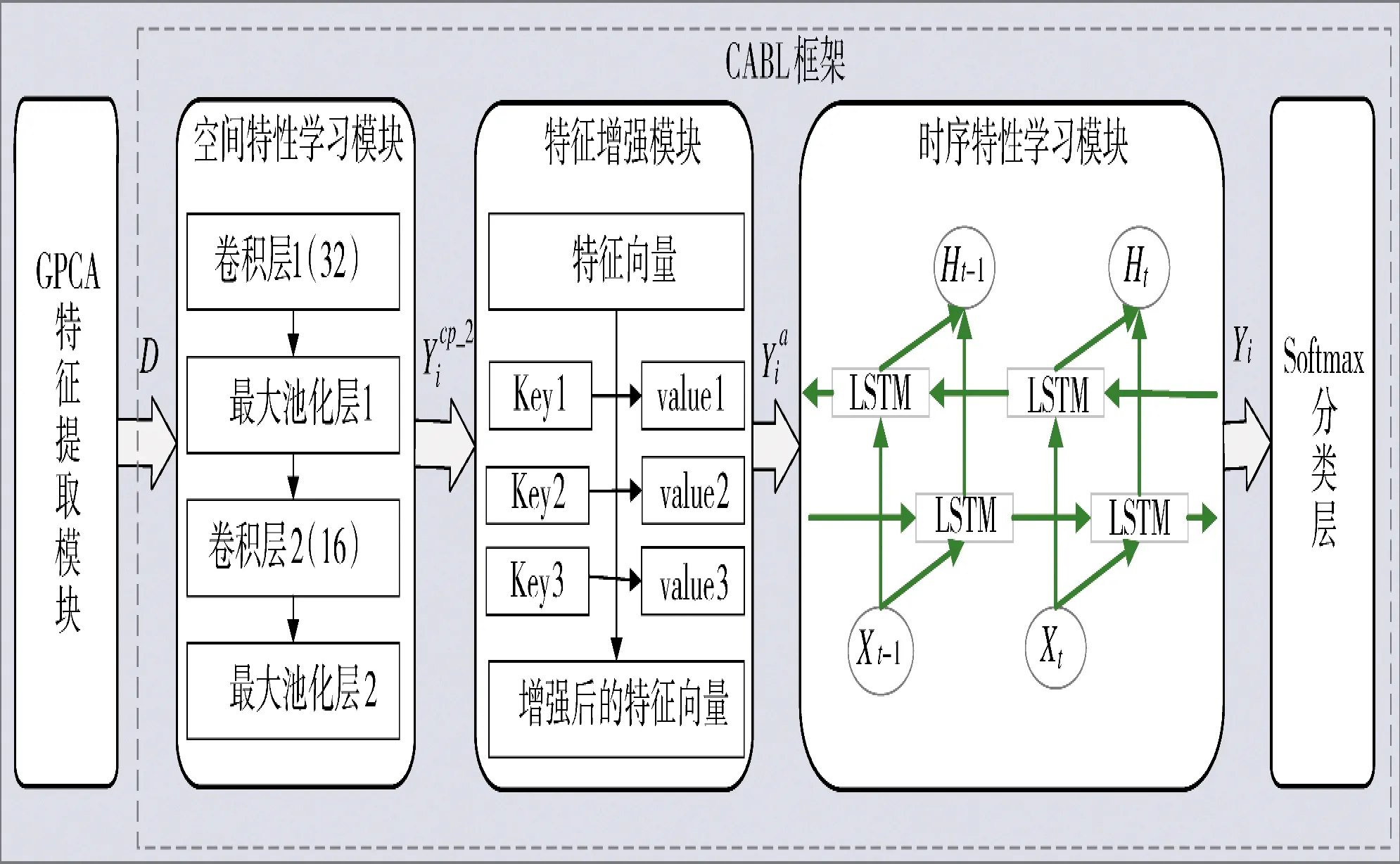
图2 GP-CABL 模型架构图Fig.2 GP-CABL model architecture
CABL 检测模型构建的步骤包括:
Step 1 空间特征学习,将GPCA 选择的最优特征集输入流量空间特征学习模块进行空间特性学习;
CNN 的输入是三通道,其格式为H×W×C,其中,H,W 是数据集的样本数和特征个数,C=1 表示文本序列。本文的卷积网络选取3×1 的共享卷积核进行卷积操作,提取局部区域的特征,具体可由式(7)和式(8)可得,其中,W 表示代表卷积核的矩阵向量,Bi表示随机偏置向量,f(·)表示非线性激活函数ReLU,该激活函数反向传播求误差梯度时导数保持不变,从而可以加快模型收敛的同时有效缓解模型过拟合。
为了更加充分学习数据特征,增加卷积层和池化层,本文构建的CABL 模型包括2 层卷积层和池化层,即对1 层CNN 学习后的特征向量利用式(10)~式(12)计算得到2 层CNN 网络学习后的特征向量。
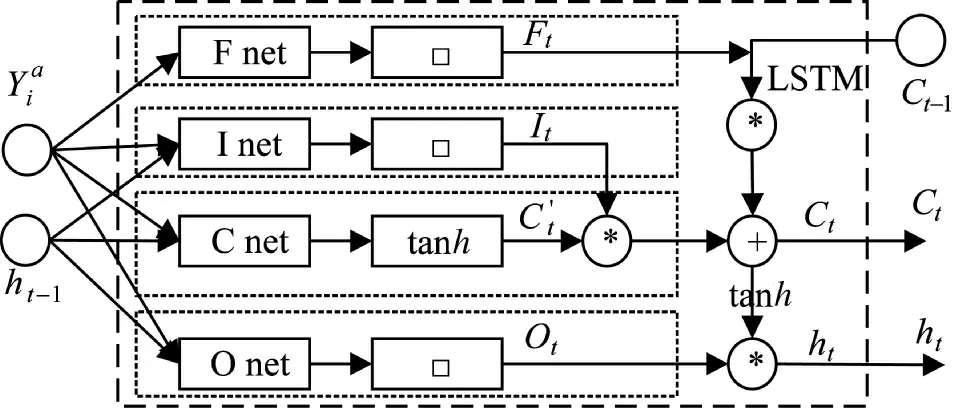
图3 LSTM 网络数据流图Fig.3 Data flow diagram of LSTM network
其中,ht表示t 时刻隐藏层的状态,对应的特征向量由式(21)表示,其中,f 表示非线性激活函数且h0=0。
Step 4 恶意流量分类,将Step3 的输出Yi利用softmax 进行归一化实现分类;
将Yi在全连接层采用softmax 进行映射到(0,1)区间内。本文进行二元分类,经过softmax 层的输出是一个二维向量,向量的第一维表示该样本属于正常的概率,第二维表示样本属于攻击的概率。对比二维向量的值,概率更大的则为预测结果,将预测结果与真实标签进行对比,计算模型分类的各项性能指标。Softmax 计算概率的方法如式(22)所示,其中,C 是分类类别的个数。
检测框架训练阶段,GP-CABL 是通过向CABL模型中加载GPCA 提取的最优特征子集,模型训练直到损失函数loss 收敛,保存网络结构参数和网络最优权重文件。检测框架测试阶段,GP-CABL 通过加载训练过程获取的最优权重文件进行模型测试,统计预测结果与真实结果的数量,形成混淆矩阵,并通过式(23)~式(27)分别计算识别精度、准确率、特异性、召回率或检测率、F1-Score 等指标。
1.4 基于贪心策略的CABL 模型调参
模型参数与其性能评价息息相关,合适的参数可以更接近模型性能上限,CABL 基于贪心策略的调参获取最优参数(包括模型学习率、迭代次数、模型隐藏层结点数量最优值)。本文结合实验环境中内存容量大小考虑决定设置批处理大小为100 进行调参实验,调参的具体步骤如下所示:
Step 1:确定CABL 模型初始学习率为0.1。
Step 2:每一步以缩小10 倍的速度降低学习率来进行模型训练,观察模型准确率和精度等指标,观察到损失函数随训练步数呈对勾形,选择损失下降最快那一段的学习率作为最优的训练学习速率α。实验发现当学习率为0.001 时,损失函数下降最快。
Step 3:固定Step2 确定的最优学习速率α,观察损失函数变化曲线,直到loss 函数逐渐趋于平稳,模型基本收敛,停止迭代,确定最优迭代次数T。
当学习率为0.001,批处理大小为100 时,模型训练的指标曲线如图4 所示,由图4 可得到迭代次数为100 时,loss 基本趋于平稳,模型基本收敛,故确定最优迭代次数为100。
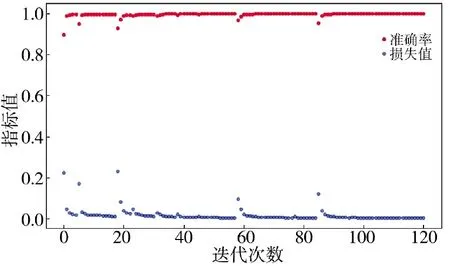
图4 GP-CABL 模型迭代曲线图Fig.4 Iteration curve of GP-CABL model
Step 4:固定Step 2、Step 3 中选择的最优学习率α、最优迭代次数T 不变,调整CNN 隐藏层结点个数和Bi-LSTM 网络结点个数,以变化趋势进行调整(CNN 隐藏层结点个数变化为:16,8->32,16->64,32->128,64;Bi-LSTM 网络隐藏层结点个数变化为:16,32,64,128),观察模型的分类准确率和训练时间,寻找最合适的结点个数。实验发现,随着隐藏层结点个数的增加,模型检测性能维持在±0.5%的区间内,而训练时间会逐步增加。本实验综合考虑模型性能和训练时间最终选择的隐藏节点个数为CNN(32,16),Bi-LSTM(64)。
基于贪心策略的调参结果如表1 所示。
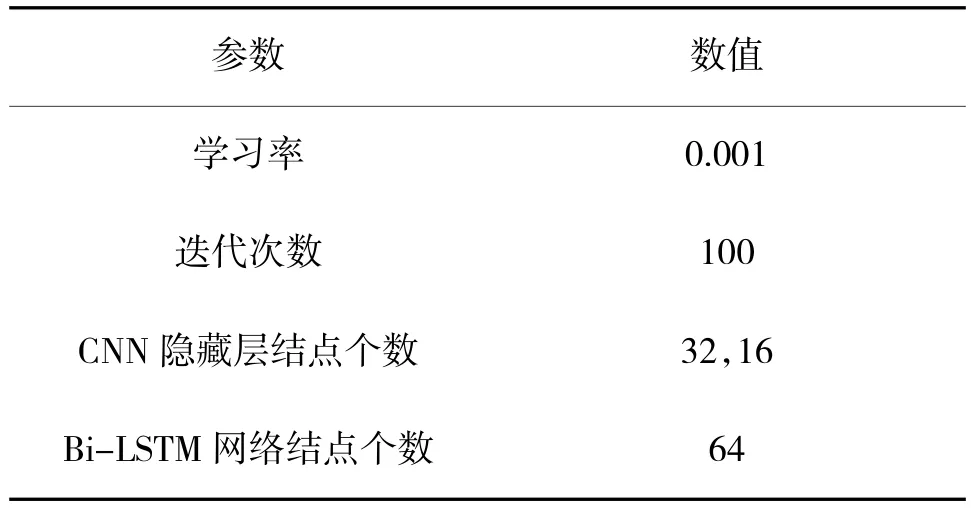
表1 GP-CABL 最优参数选择结果Table 1 Optimal parameter selection results of GP-CABL
2 实验及性能分析
2.1 实验评价指标
GP-CABL 性能评价指标包括混淆矩阵[14]、精度、准确率、特异性、检测率和F1-Score,其计算方法见式(23)~式(27)。混淆矩阵也称为误差矩阵,用来表示一个分类器结果的矩阵,其矩阵表示如下页表2 所示。
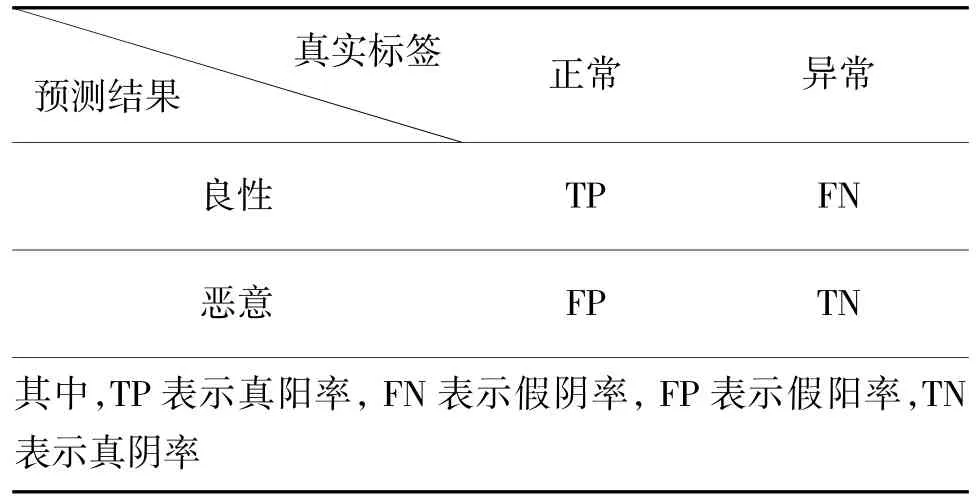
表2 混淆矩阵Table 2 Confusion matrix
其中,β 表示召回率与精度的权重比,如果认为精度和召回率同等重要,则β=1。
2.2 实验环境配置
GP-CABL 框架在featurize 官网租用云算力进行仿真,实验环境如表3 所示。

表3 GP-CABL 框架实验环境配置表Table 3 Experimental environment configuration table of GP-CABL framework
2.3 实验数据集
本文采用NSL-KDD 数据集[15]进行仿真验证,该数据集包括41 个特征和1 个类标识(标记正常或恶意流量),其中,9 个特征是离散型数据,其他均为连续型,因此,在进行训练前先对连续型数据进行二值转换、标准化等预处理操作。数据集中的恶意流量包括4 大类(DoS、Probing、R2L、U2R),共计22 种训练攻击类型,具体类型参如表4 所示。本文将20%的KDDTrain+数据集(494 022 条数据)按照8∶2 的比例划分为训练集和测试集进行模型训练和验证。

表4 NSL-KDD 数据集攻击类型Table 4 Types of NSL-KDD dataset attacks
2.3.1 数据预处理
针对NSL-KDD 数据集数据格式异构、规格不统一的情况,实验中依次采用二值转换、标准化、One-Hot 编码方式进行了数据预处理。
Step 1:二值转换。
利用字典的键值对实现字符型特征到数值型特征的转换,具体转换情况如下页表5 所示。
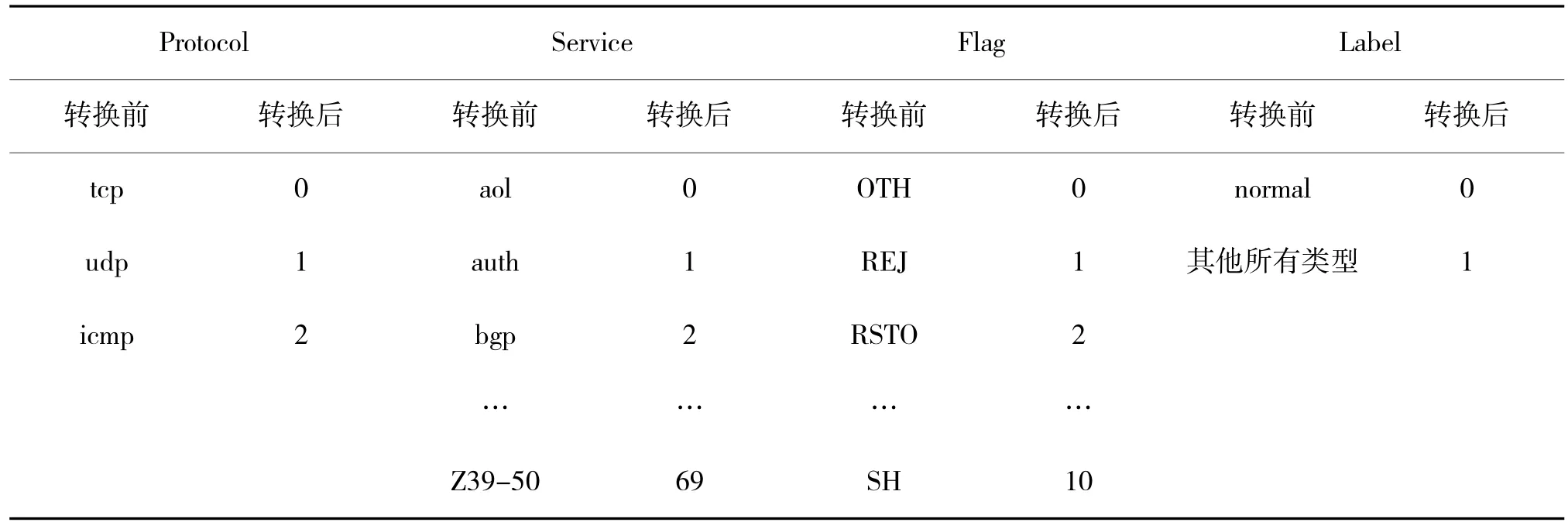
表5 二值转换对照表Table 5 Binary conversion comparison table
Step 2:标准化,标准化方法如式(28)所示。
Step 3:One-Hot 编码。
实验中借助Python 的numpy 包对数据标签la bel 进行了One-Hot 编码,将良性数据“0”使用“10”表示,将恶意数据“1”使用“01”表示,这样模型训练时计算相似度更合理。
2.3.2 特征提取
GPCA 将NSL-KDD 数据集的特征构造为30维新特征进行模型训练,主要过程为:1)保证训练过程中的各项参数不变,主因子个数从20 开始,以5 为步长进行增加;2)观察模型评价指标的变化趋势,寻找最值点对应的主因子个数k。不同k 值对应的性能指标如图5 所示。由图5 发现随着主因子个数的增加,模型准确率和精度等指标也随之增加,从30 之后,模型准确率和精度等指标随着主因子个数增加而下降,因此,取最优主因子个数为30。
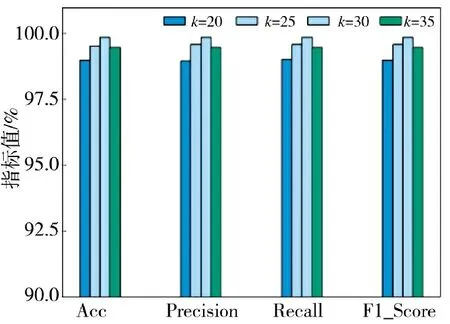
图5 不同K 值对应的性能指标Fig.5 The corresponding performance indicators for different K values
2.4 实验结果与分析
2.4.1 实验结果
GP-CABL 通过贪心策略的调参方法确定两层卷积层的隐藏结点个数分别为32 和16,Bi-LSTM结点个数为32,学习率为0.001,迭代次数为100,特征提取确定GPCA 的主因子个数为30 时,模型性能最好,模型准确率达到99.865%,精度达到99.868%,检测率达到99.861%,具体实验结果如表6 所示,模型测试的混淆矩阵如图6 所示。
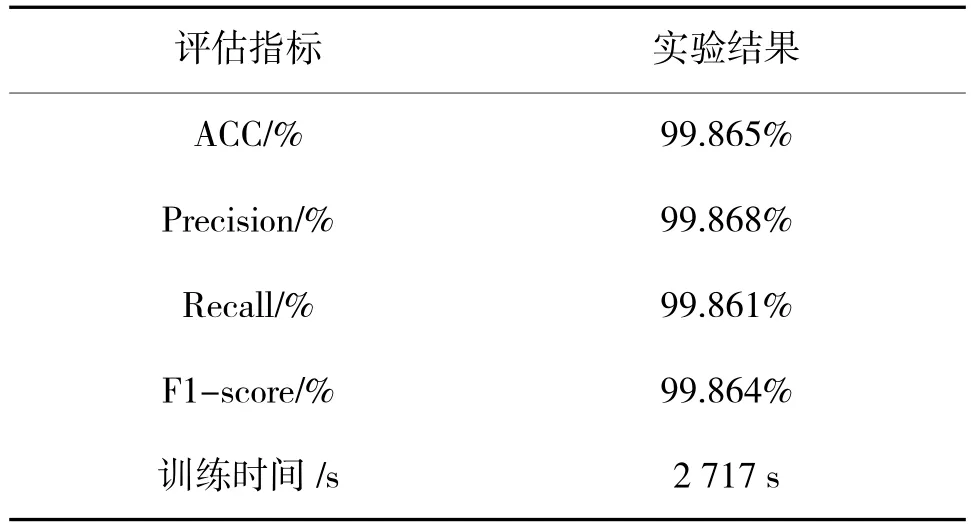
表6 GP-CABL 检测框架实验结果Table 6 Experimental results of GP-CABL detection framework
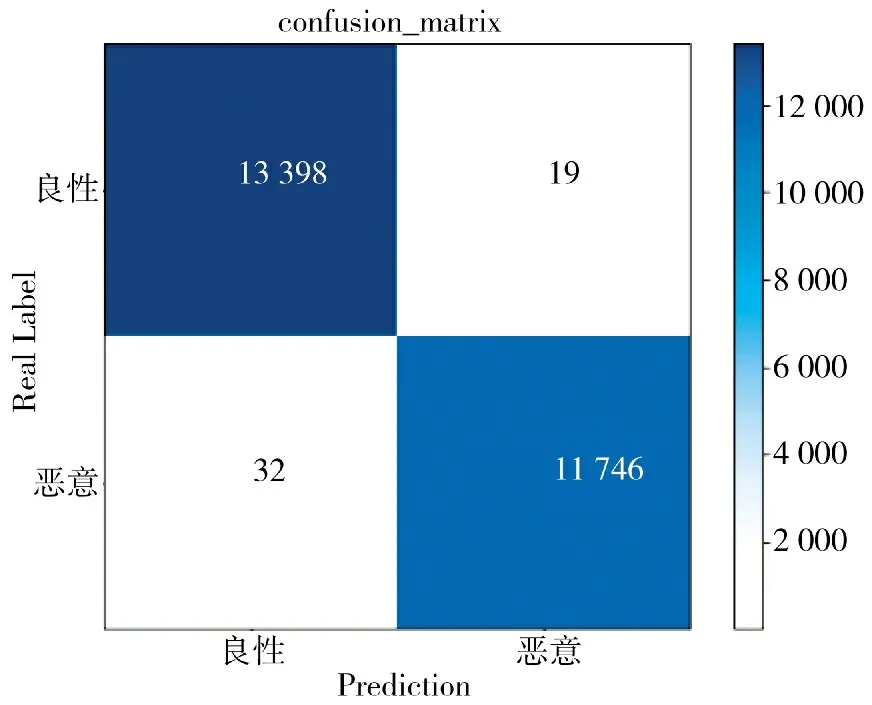
图6 GP-CABL 模型测试的混淆矩阵Fig.6 Confusion matrix for GP-CABL model testing
2.4.2 对比实验
为验证本文所提出的GPCA 特征提取算法的优势,在2.2 节所列实验环境下,本文将未进行特征提取的CABL 模型和GP-CABL 模型进行对比,对比情况如表7 所示。由表7 可以发现,未进行特征提取的CABL 模型在各项检测性能上稍逊于GP-CABL,而且在训练时间上,GP-CABL 对比CABL 模型缩短了3 476 s,因此,可以证明GPCA 特征提取模块不仅可以提升模型检测性能,也能大幅缩短模型训练时间。
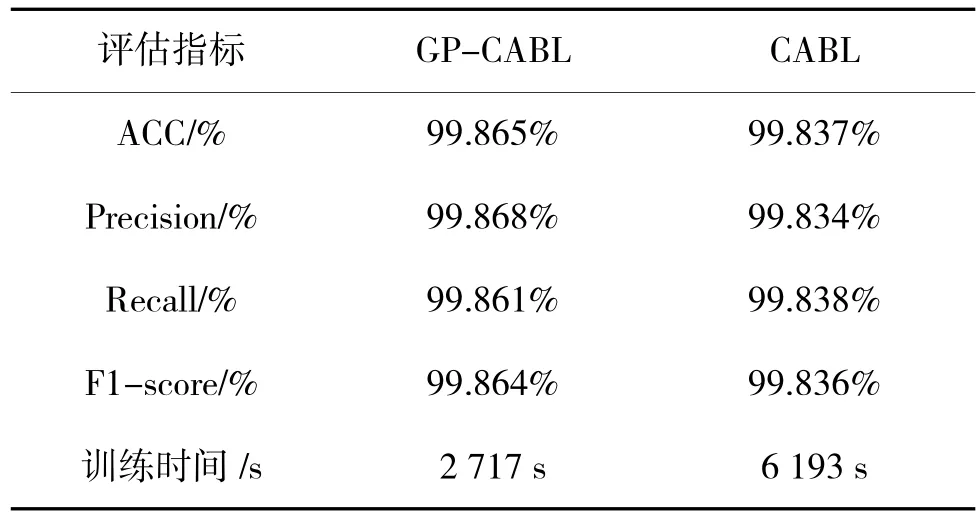
表7 GP-CABL 与CABL 模型对比Table 7 Comparison of GP-CABL and CABL models
为验证GP-CABL 的性能,在2.2 节所列实验环境下,分别与DT、AdaBoost、KNN、LR 等经典机器学习算法进行对比,如表8 和图7 所示,由表8 可以看出GP-CABL 检测框架对比DT、AdaBoost、KNN 3种算法性能提升约3.1%,对比LR 算法性能提升约12%左右,由图7 可以看出GP-CABL 在ACC、Precision、Recall 和F1-Score 方面都大幅度优于各类机器学习方法,因此,证明GP-CABL 较经典机器学习算法具有更好的检测性能。
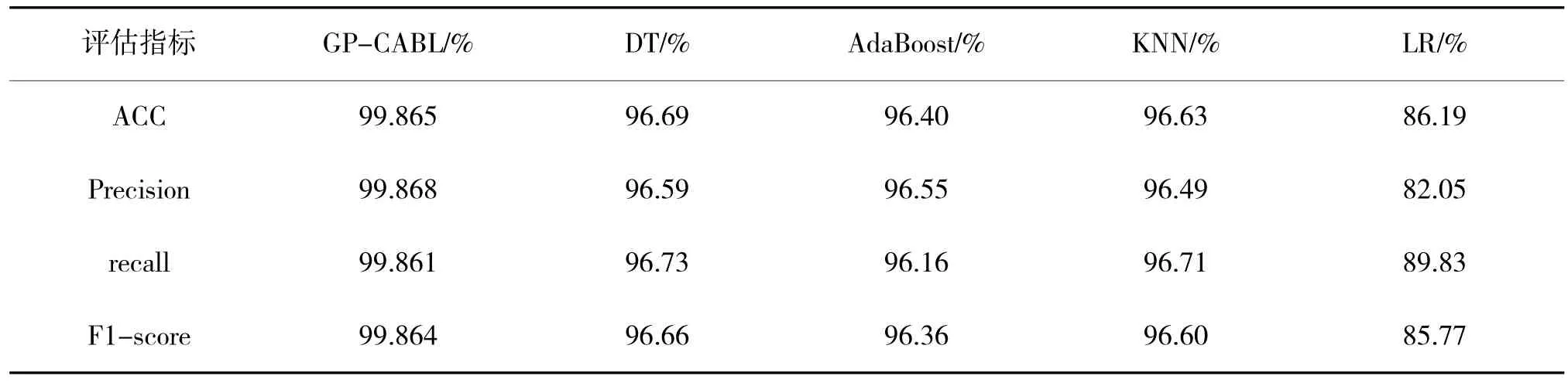
表8 GP-CABL 和经典机器学习算法实验对比结果Table 8 Experimental comparison results of GP-CABL and classical machine learning algorithms
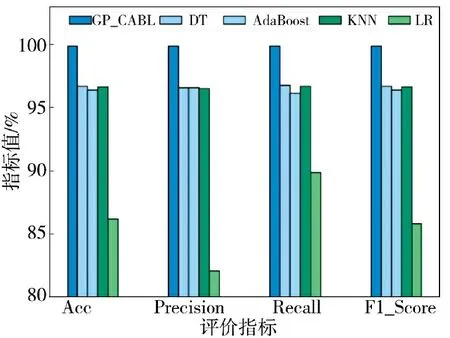
图7 GP-CABL 模型与经典机器学习算法性能对比情况Fig.7 Performance of GP-CABL model compared with that of classical machine learning algorithms
为进一步验证GP-CABL 性能,在2.2 节所列实验环境下,与文献[9]和文献[16]中提出的Bi-LSTM和CNN+Bi-LSTM 模型进行了对比。对比结果分别如表9、图8 和图9 所示。由表8 发现,GP-CABL 较文献[9]模型在ACC、Precision、Recall 和F1-Score评估指标方面提升约1%,但大幅降低了训练时间减少达4 567 s,GP-CABL 较文献[16]模型在各评价指标中提升约0.02%,训练时间降低815 s,其主要原因在于GP-CABL 采用GPCA 优化了网络流量特征,降低了训练开销;采用CABL 深入学习流量空间和时序特征使其在检测精度等方面获得更好的表现,如图8 和图9 所示。
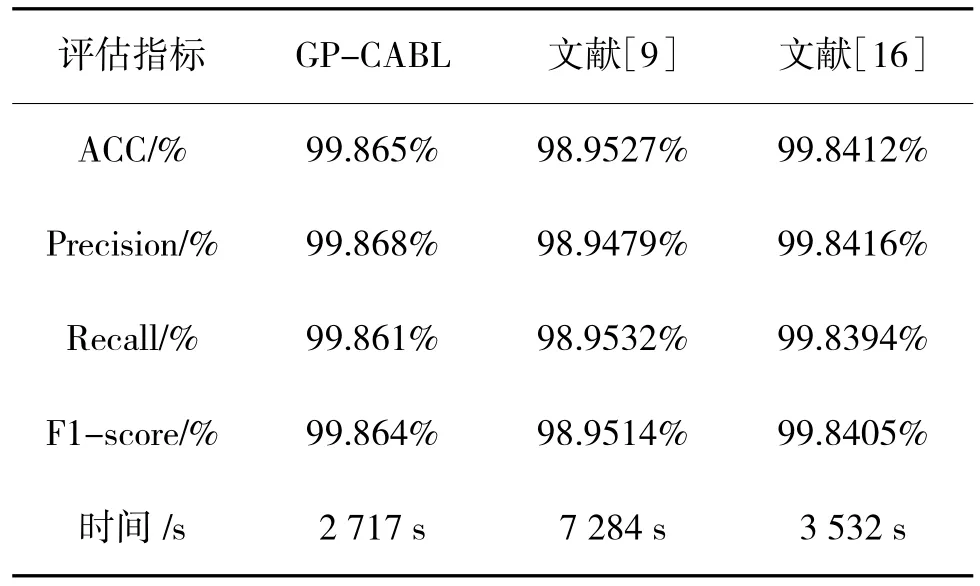
表9 GP-CABL 和文献[9]、文献[16]实验对比结果Table 9 Experimental comparison results of GP-CABL and literature 9 and literature 16
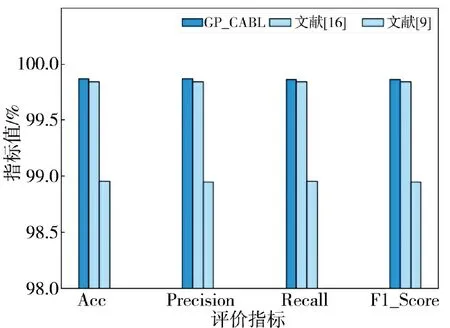
图8 GP-CABL 模型与其他模型评估指标对比Fig.8 Evaluation index comparison of GP-CABL model and other models
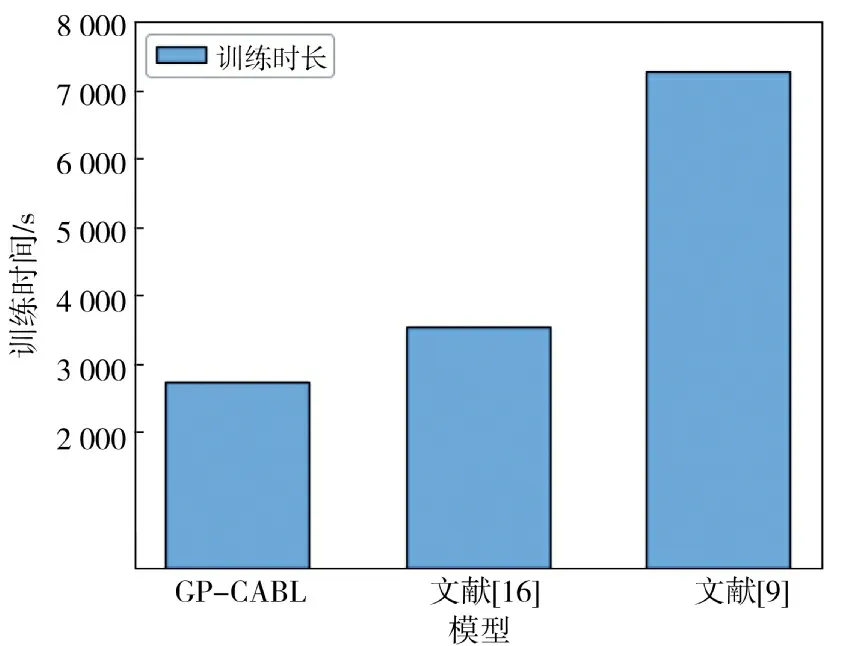
图9 GP-CABL 模型与其他模型训练时间消耗对比Fig.9 Comparison of training time consumption of GP-CABL model and other models
3 结论
本文基于深度学习技术提出了针对网络攻击的GP-CABL 检测框架,GP-CABL 基于贪心主成分分析构建的特征优化模型,能够从高维网络流量特征中获取最优特征集,大幅降低了模型训练中的计算开销,提出的CABL 检测框架能够充分学习网络流量的空间特性和时序特性,获得更高的检测精度,基于NSL-KDD 的实验表明其较当前其他研究在检测精度和时间开销方面取得了明显的提升。然而参数调优阶段选取基于贪心策略的方法容易陷入局部最优,借助动态规划算法寻找模型的全局最优参数,将是未来研究中需要改进的问题。

