数据和知识驱动的空战目标集群类型综合识别

张会霞，梁彦，*，马超雄，汪冕，乔殿峰

1．西北工业大学 自动化学院 信息融合技术教育部重点实验室，西安 710129

2．中国电子科技集团第二十研究所，西安 710068

在信息化条件下，空战战场环境日渐复杂，多平台协同作战正在逐步成为空战的主流［1-2］。集群通过实时动态编组，在线任务分配、集群协同突防的方式，实现了以量取胜、动态聚能、精准释能的饱和攻击，整体效能大于单个效能的累加和，即作战效能涌现“1+1＞2”的系统增效［3-4］。因此，如何根据空战战场态势信息进行实时、准确的集群场景分析和威胁评估是提高我方作战成功率和生存率的关键。亟需综合利用数据和知识对集群进行由粗到细的精细化分析，辅助指挥员快速准确全面理解战场态势。

聚类不需要对数据的标签有初步的认识，它处理未知区域的数据结构划分，也是进一步研究集群精细化识别的基础［5］。集群分析中聚类的主要任务是基于正确的相似性度量将数据点划分为适当的类。聚类算法一般分为以下几种： 划分方法、层次方法、基于密度方法和基于网格方法。K-means 算法高度依赖一组给定的初始聚类中心，聚类结果容易受到离群值的影响［6］。相比之下，分层方法以聚集或分裂的方式对数据集进行多级分区。基于密度的聚类是一种非参数方法，将聚类视为高密度数据点，由低密度数据点组成的连续区域相互分离，可以检测任意形状的聚类［7］。但是，适当的阈值设置因数据集的不同而不同，仍然没有有效的方法来预先确定这些阈值。作为一种流行的基于密度的聚类算法，快速搜索和发现密度峰值聚类（Density Peaks Clustering，DPC）算法也可以处理非球形数据，不需要手动指定类别的数量［8］。DPC 算法的参数选择比DBSCAN 算法更容易。因此，出现了许多关于DPC 的有价值的工作。HaloDPC 算法不仅提出了合理的Halo 处理方法，而且改进了聚类结果［9］。DPC-KNN 算法将k最近邻的思想融入到距离计算和分配过程中，使分配过程更加合理［10］。然而，这些DPC 算法的变体对于分布不平衡的聚类的划分并不是很有效，因为它们只使用一个指标（近邻点的距离）来同时处理内部点和边界点。因此，将上述2 个指标结合起来，增强寻找边界点的能力，使集群聚类准确分离是有价值的研究。

集群识别是态势推理的重要组成部分，且此识别过程主要依据基于D-S 证据、专家系统、模板匹配、贝叶斯网络等方法。针对稀疏信息环境下的数据融合问题，基于D-S 证据推理设计了判断战场事件可靠性的框架［11］。一种基于知识的海战场态势评估辅助决策系统利用知识发现技术对战场数据进行分析，综合利用数据、知识和模型实现态势评估［12］。基于模板匹配的计划识别与态势评估系统通过识别模型以多假设的形式描述个体的当前和未来的活动［13］。然而模板库的构成用到大量的军事规则和领域专家知识，实现难度大、维护更新难；采用分层贝叶斯网络（Bayesian Network， BN）对作战计划分级建模表示，通过提取实时的战场事件及当下的作战单元动作，实现分层BN 结构构建［14］。BN 利用网络参数的实时调整能够动态地适应复杂多变的战场环境，实现对敌方群类型/意图的准确推理［15-16］然而在日益复杂的战场环境中，传统给定参数的贝叶斯网络不能满足日益复杂的集群作战中集群推理分析，仅仅依靠专家经验确定或数据学习2 种方式均存在弊端。因此，需要充分利用数据和知识双重优势，还需考虑数据在时间上相关性，实现复杂战场环境下集群类型推理优化和提升。

军事强国均在加紧研究适用于集群的分析与应用，美国多个研究机构纷纷围绕无人机“蜂群”作战展开关键技术试验，“小精灵”“郊狼”“低成本无人机集群技术”等项目不断出现新的研究突破［17］，面对紧张的国际形势，中国在作战集群方面研究的紧迫性日益凸显。集群作战要在联合部队内建立灵活以及具有适应性的编队，改变部队部署态势能够加强对敌威慑。随着数据的收集和专家经验的总结，典型作战样式被充分挖掘，分析出其主要包括：“忠诚僚机”战术骗扰、有人／无人智能协同、“蜂群”智能协同等典型样式［18］。有学者对目标估计和群状态（群大小、形状等）进行估计，提出了群体目标的动态模型和观察函数，并构建估计状态集的邻接矩阵，实现战斗机编队跟踪和群形状估计［19］；还有将集群整体作为一个扩展目标，通过建立更符合实际的量测模型，提升了对集群的跟踪精度［20］。群意图分析方面，在综合群目标的基本组成、公开活动、作战条例等各类信息构建的知识图谱基础上，提出一种多实体分层贝叶斯网络来推理目标意图［21］；利用集群情景分析法对系统内外相关问题进行系统分析，设计出多种可能的未来前景，对系统发展态势做出自始至终的情景与画面描述，有效描绘未来变化的进程［22］。群任务分派方面，集群在执行任务过程中，不同飞机各司其职，在有限资源下进行资源分派，一方面保护自身安全，一方面协同完成指定作战任务［23-25］。随着未来作战节奏与进程加快，如果能够预判出集群编队类型，就可辅助指挥员分析出敌方下一步或几步行动，提前做出部署，建立作战优势。目前，集群相关研究更多停留在目标的几何队形识别、集群内部资源的任务分派，但是集群类型作为集群任务、意图等紧密相关的重要因素缺乏深入研究。综上，敌方集群类型精细化识别不仅是国家在应对国防安全所面临的重要难题，也是学术研究中值得探究的内容。

基于上述学术研究和应用需求讨论，本文提出分层精细化推理的目标集群识别框架，预识别层检测目标运动过程中的集群的分群/合群，得到群的初步识别结果；在再识别层综合分析集群执行任务、运动、电磁等多种特性，在此基础上构建了集群类型推理网络结构，进一步又设计了基于专家经验及少量数据样本的推理网络参数学习方法，得到完整的推理网络，实现在集群内部进行精细化推理。该研究的特点主要包括：提出集群类型推理的新问题，构建了分层精细化推理的集群场景识别框架；所构建的集群推理网络发挥了知识和数据双重优势，具备从粗到精的集群目标识别能力，实现集群的精细化识别与判读。

1 问题描述

不同于传统的作战样式，集群作战要在联合部队内建立灵活以及具有适应性的编队，通过改变部队部署完成对应的执行任务。不能仅从组成单元的行为推断，只分析局部不可能得出集群/整体性推理结果（集群类型、意图等）。空中作战不断演变的特点使态势要素间的关系更加复杂多变，如图1 所示，单元之间组合表现出不同的飞行速度、高度、飞行目的地等特点，这些特点本质上反应的是集群编队类型，准确综合分析出集群编队的类型会辅助指挥员对作战态势全面理解，亟需对集群编队类型进行精细化识别。

根据图1 反应的战场中集群协作执行任务，其隐含的集群类型推理识别正是战场态势分析的关键要素，如何在复杂战场环境下对集群类型有效识别主要面临两大问题。

问题1如何适应复杂多变的集群作战场景综合分析，优化问题如下：

最优：分层推理框架。

问题2如何对集群精细化分析，主要是从推理网络的结构确立和参数获得两方面，优化问题具体如下：

其中，θ为推理网络参数；γ为推理网络结构。

综上，亟需对整个集群进行快速的划分，通过借助多元知识和多特征综合，动态推理出集群类型，输出集群编队推理结果的概率度量。

2 基于数据和知识的推理识别网络构建

复杂战场环境下集群在执行任务中随着靠近任务区域，集群开始紧凑，协同执行任务，如图2 所示。然而如何在集群有效聚类分群之后对集群类型进行精细化仍是开放性话题。

图2 目标集群态势变化Fig.2 Change for target cluster situation

本文拟综合数据和知识的优势使设计框架具备空间要素聚合，时间动态推理的能力，达到渐次提升集群识别精度目的，给出框架设计图如图3 所示。对专家知识、领域知识、作战规则等多元充分分析，即知识收集，用于抽取推理识别网络构建时用的约束条件和规则，在此基础上设计分层精细化推理的集群类型识别来提高集群编队识别的精度。首先依据典型场景（转场、扫荡等）利用基于相邻点距离和数据点非对称度量的有效局部密度计算方法进行初步的集群空间划分；然后从功能性的角度出发，在多元知识里提取了关键约束条件和因素之间的相关性，综合多方面因素，设计了集群类型推理网络结构；最后基于所设计的一种基于专家经验及少量时间序列样本参数学习方法，通过有限数据的充分利用得到推理识别网络的参数修正，进而在集群内部进行精细化推理，识别出集群类型。

图3 数据和知识驱动下的目标集群综合推理识别Fig.3 Comprehensive reasoning and recognition of target clusters driven by data and knowledge

为让本文所设计框架和算法更加明了，给出算法流程框架图如图4 所示。在图4 中给出算法流程架构图，为更清晰的了解本文算法，给出本文伪代码如算法1 所示。

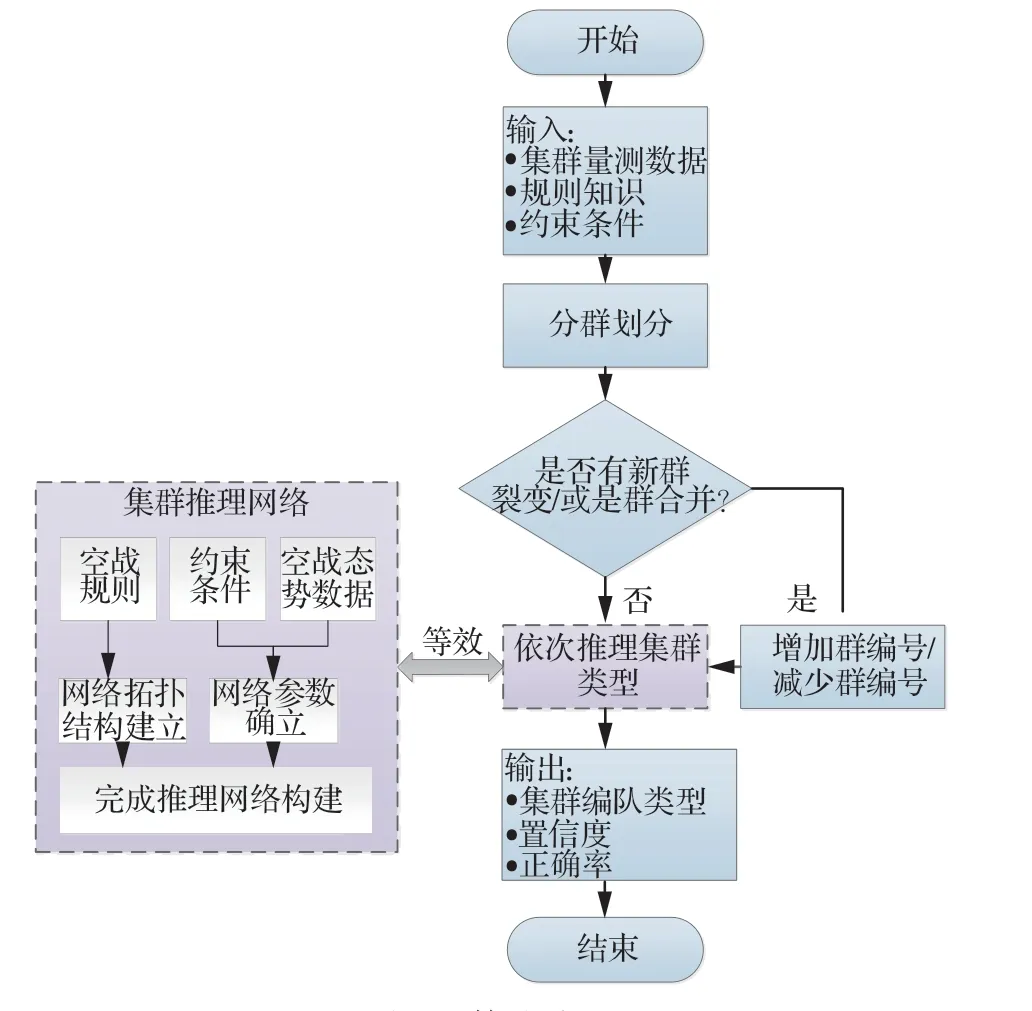
图4 算法流程Fig.4 Algorithm flow

针对图3 所示的研究框架图，研究内容可以分成3 部分：基于边界检测的目标集群划分情况、推理识别网络中的结构构建和参数学习，具体模块依次详细展开如2.1～2.3 节所示。

2.1 基于边界检测的目标集群划分

对于给定的一维数值属性数据集X=[x1，x2，…，xm]T，不对称的比例αxc定义为

式中：Small(X，xc) 表示小于xc的元素个数；Large(X，xc) 表示大于xc的元素个数。对于均匀分布的数据集中靠近中心的点，其αxc的值将会很小。式（1）可以通过数据集中元素的不对称性来判断矩阵的位置。

算法1 数据和知识驱动的集群类型识别1.输入：知识收集模块，提取规则和约束条件，以及实时的传感数据；2.for 当前时刻所有目标位置量测；3. 检测目标集群划分情况：if 出现分群合群顺序执行4；else 没出现分群合群跳转5；4.增减集群编号情况；5. for 对当前目标集群数量，读入每个集群其他信源；6. 经推理网络识别每个目标集群的所属类型；7. end；8.end；9.输出：集群类型、置信度及正确率。

对于数据集Xm×n中一个给定的点xc=[xc1，xc2，…，xcn]，如果它位于数据集的边界，则它在数据集中具有很强的不对称性，否则就是内部核心点。

k最近邻采样总是将由k个数据点组成的局部空间提取为动态采样空间，因此能更好地反映局部空间的分布特征。内点的k最近邻点在其周围均匀分布，即内点的k最近邻点的非对称性较弱。相反，如果边界点的k最近邻点非均匀分布，则边界点的最近邻点的非对称性是较强的。定义非对称度量AM 如下：

式中：k是Xc m×n中第d列Xd的最近邻个数，k的值应根据数据集的大小来确定，它主要用于控制最近邻点的个数来计算非对称度量。由式（2）可以看出，簇内点的非对称性较弱，而边界点的非对称性较强。AM 的值通常在簇内区域相对较大，而在簇边界区域相对较小。因此，非对称度量可以用来检测边界点。

本文聚类方法的决策图包含了每个点的2 个量：局部密度ϑ(xc)和距离δxc。本文算法充分利用局部密度ϑ(xc)和非对称度量AM2 个指标的互补性，构造了xc的一个新的局部密度，ϑ(xc)和δxc的计算过程。

式中：0 ≤α≤1，0 ≤β≤1；dc为可调参数，dc=v·m，v为唯一的参数，局部密度由dc的高斯核估计，它为集群分配点提供了较为严格的标准。xd=［xd1，xd2，…，xdn］，d(xc，xd)是xc和xd之间的欧式距离。在本文算法中决策图的另一个量，距离δxc为

上述过程中关键步骤是结合2 个指标计算局部密度，可以更好地识别边界点，从而使不同集群聚类，最终达到提高聚类效果的目的。本文设计了适用动态复杂战场的计算方法，如算法2所示。

算法2 基于边界检测的集群聚类1.输入：样本点Xm×n、距离参数dc 和最近邻个数k；2.使用欧式距离计算任意2 个样本点之间的距离；3.根据式（3） 计算点xi 的ϑ(xi)（ i=c，d）；4.根据式（4） 计算点xi 的δxi；5.绘制决策图，选择聚类中心；6.将每个剩余的点分配到最近的具有更高局部密度的点上；7.输出聚类结果。

面对作战情况复杂多变的情况，集群的分布往往是不平衡的，该方法能有效解决这类问题。

2.2 推理识别网络结构模型构建

推理识别网络结构包括可以观测到的证据节点和需要推理其后验概率的隐节点。在基于动态贝叶斯网络的场景识别过程中，实质上是对目标的集群编队进行推理。在战场中集群编队类型主要通过集群组成、任务特性、运动特性3 方面体现，模型结构中的证据节点主要包括集群编队类型相关的要素［23］。最后在专家知识、领域知识、作战规则等多元的可以提供目标集群的运动学特征、结构特征、电磁特性多方面的规则约束和条件约束，在此基础上依据任务等要求的不同对集群编队类型要素进行提取，选取最为重要的以及对集群编队类型影响程度较大的因素［17，22］，通常用于集群编队类型推理的要素主要包括4类。

1） 运动特性

飞机运动模式是什么类型是判断集群编队样式的重要因素。主要影响因素有集群速度、高度、机动模式。根据参考文献［21］，速度通过模糊划分可以分成小、中、大3 类； 高度也是同样的处理方式，通过模糊划分可以分成低、中、高3 类，因为集群类型会对应不同的飞行高度；机动模式是在飞行过程中产生的具有特定模式的状态［24］，包含：盘旋机动、S 形机动、爬升/俯冲机动、无明显机动几种典型的机动样式。

2） 任务特性

飞机集群编队的执行任务确定，是编队样式划分的另一重要因素。打击任务为例：候选的打击点和打击方向成为关键，即任务特性反应在与我方不同目标的接近速率和执行任务飞行方向。因此，任务特性的主要影响因素有集群接近打击点距离变化率和任务飞行方向。根据参考文献［21］，接近打击点距离变化率是接近几个重要价值目标的距离变化率，通过模糊划分可以分成3 类：靠近、无明显变化、远离；任务飞行方向是指接近重要价值目标［24］，设定的高价值目标包括：高价值目标、通信目标、无明显目标。

3） 集群结构特性

由集群编队内单个飞机的机型识别结果计算出的集群结构，也是推理飞行编队样式的重要因素。可通过单架飞机的机型种类置信度算出集群成员机型比例来确立集群结构特性，此外，队形也是集群结构特性的重要因素，主要考虑集群机型占比和集群编队队形2 个影响因素［23］。集群机型占比通过关键机型数量的占比可以分成3类：战斗机、干扰机、预警机。

4） 电磁信号特性

敌方飞行器雷达工作时释放的电磁信号与自身功能性密切相关，从捕获的电磁信号可以发现敌方飞行器雷达的工作模式，进而为兵力构成分析提供依据支撑，根据参考文献［21，25-26］，主要考虑因素为工作模式和电磁开关机，同时电磁信号特性可以通过工作波段来进行类型划分，主要包括：UHF 波段、L 波段、S 波段、X 波段、Ku波段，其代表了所处的工作模式。

由上述分析，不仅可以确定贝叶斯网络模型的节点，还可以得到初始网络的构建，在初始网络中加入时间因素，确定基于动态贝叶斯网络的集群类型推理模型结构如图5 所示。

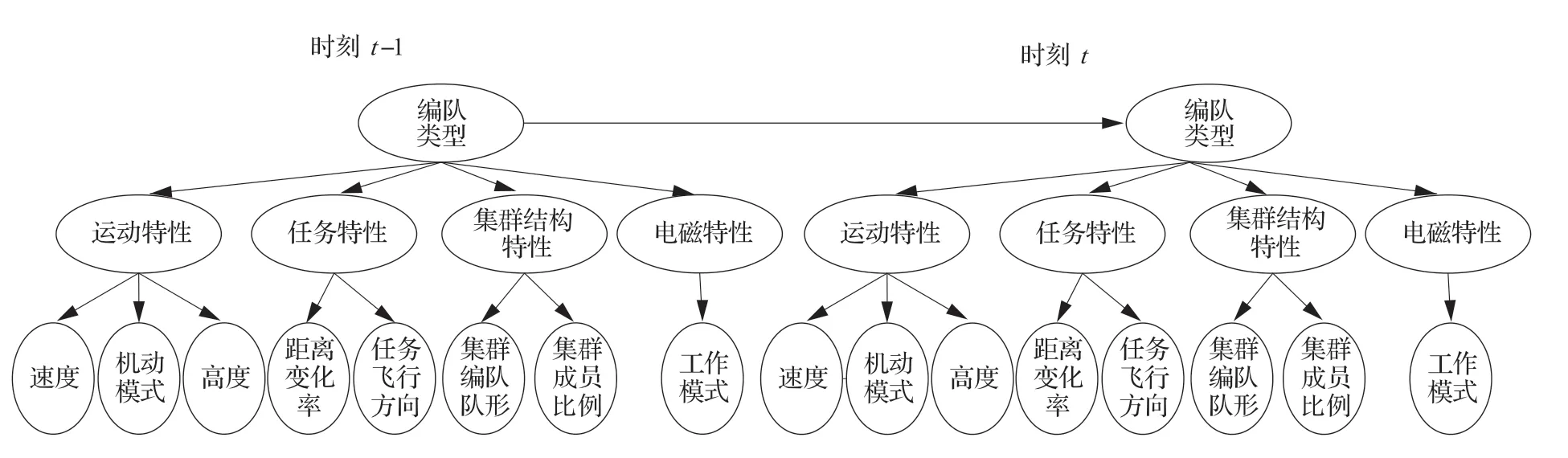
图5 空战动态贝叶斯网络推理模型Fig.5 Dynamic Bayesian network inference model in air combat

图5 中各节点状态空间具体如表1 所示。表1中在仿真的标签为目标速度=｛1，2，3｝=｛小，中，大｝；目标高度=｛1，2，3｝=｛低，中，高｝；机动模式=｛1，2，3，4｝=｛盘旋机动，S 形机动，爬升/俯冲机动，无明显机动｝；任务飞行方向=｛1，2，3｝=｛高价值目标，通信目标，无明显目标｝；距离变化率=｛1，2，3｝=｛靠近，无明显变化，远离｝；集群成员比例=｛1，2，3｝=｛战斗机，干扰机，预警机｝；集群队形=｛1，2，3｝=｛“8”字型，菱形，一字型｝；雷达工作模式=｛1，2，3，4，5｝=｛ UHF 波段，L 波段，S 波段，X 波段，Ku 波段｝；运动特性=｛1，2，3｝=｛高空盘旋，低空搜索，定高巡航｝；任务特性=｛1，2，3｝=｛指挥控制，快速打击，释放干扰｝；集群结构特性=｛1，2，3｝=｛预警编队结构，战斗编队结构，干扰编队结构｝；电磁特性=｛1，2，3｝=｛高频段，低频段，中频段｝；集群编队类型=｛1，2，3｝=｛预警编队，扫荡编队，压制编队｝。

表1 贝叶斯网络节点状态空间Table 1 Bayesian network node state space

2.3 基于参数学习的集群编队类型推理模型

完成聚类分群划分之后，需要对集群的内部进行精细化分析，设计了基于参数学习的动态推理网络具体如2.3.1 节所示。

2.3.1 推理网络的参数学习算法设计

在现有的小数据集下的贝叶斯网络参数学习方法中，估计方法是学习效果较好的参数学习方法之一，相比文献［27］的静态推理，未考虑数据在时间上的相关性，考虑使用具有时序关系的样本数据，达到对推理网络的转移概率的参数学习的目的，即为动态定性最大后验概率（Dynamic Qualitatively Maximum A Posterior，DQMAP）该方法得到网络参数后验概率如下：

式中：θ代表网络参数；G为网络结构；ψ为参数约束；C=log10P(D|ψ，G)通过如下形式得到

式中：Nijl表示训练样本数据中节点i的父节点处于第j组合状态条件下节点i取第l状态的数据统计量；n、q、r均是常数值。

网络参数先验分布的定义为

给定ψ和G，这组先验参θijl定义了一类先验网络，如果在一个先验网络中采样A次，即等价样本量，则样本中满足(Xi=l，pa(Xi)=j)的数目等于Mijl=A×P(Xi=l，pa(Xi)=j|ψ)，Mijl定义为虚拟样本量，P(Xi=l，pa(Xi)=j|ψ)满足全部已知参数约束。通过定性最大后验概率估计得到参数的具体形式：

式中：W是采样参数的数量；Pw(Xi=l，pa(Xi)=j|ψ)满足所有已知参数约束。定性最大后验概率估计得参数的对数形式：

基于定性先验知识ψ的先验网络集合增加了数据样本中的统计量，并定义一类后验概率。通过将样本统计信息投影到由先验知识定义的先验参数空间上，获得参数的后验概率集。对上述函数求解得贝叶斯网络参数的定性最大后验估计：

对于推理网络来说，其参数由条件概率和转移概率组成，在式（10）基础上考虑使用具有时序关系的样本数据，实现对动态推理网络的转移概率的参数学习。本节设计的推理网络参数方法，具体如算法3 所示。

算法3 D-QMAP 参数估计1.输入：M 具有时间关系的序列样本数据 D={ D1，D2，…，DM}，参数约束ψ，网络结构G，节点集E={ X t1，X t2，…，X tN } (t=1，2 )；2.对于t=2 时间片中每个节点X 2i (i=1，2，…，N )， N 为常量；3.计算条件概率：对于M 时间序列样本数据，统计同一时间片内的节点状态统计量Nij 和Nijl，父节点属于当前时间片即pa(X 2i)∈X 2i (i=1，2，…，N )；4.判断此时节点是否与前一时间片里的节点有时间转移关联，若没有，转至6，若有转至5；5.计算相应的转移概率：对所有时间序列样本数据，统计相邻时间片间M-1 个节点转移状态统计量Nij 和Nijl，父节点属于前一时间片即pa(X 2i)∈X 1i (i=1，2，…，N )；6.通过式（8）满足参数约束的采样条件概率和转移概率分别对其平均后得到满足推理网络参数约束的整体参数P(Xi=l，pa(Xi)=j|ψ)；7.通过交叉验证方法划分样本数量A；8.利用式（10）得到条件概率和转移概率对应的估计值；9.输出：最优推理网络参数θ*。

上述方法达到了场景样本数据小的情况下，也能满足多元知识的推理网络参数学习的目的。

2.3.2 参数学习

本节利用D-QMAP 方法为2.3.1 节提出的推理网络参数进行学习。首先需要获取训练样本以及专家经验提供的参数约束信息。对于训练样本方面，根据不同类型目标在不同集群类型下执行作战任务时的运动状态，从而得到目标高度、速度、距离、执行任务飞行方向、机动类型等信息，再综合不同任务想定下雷达状态等其他要素信息，将其进行预处理后共同作为参数学习的数据样本。表2 给出了3 种典型的编队样式的特性，随机包含10 个时刻的训练数据具体样式如表3 所示。

表2 集群编队类型特征Table 2 Characteristics of cluster formation

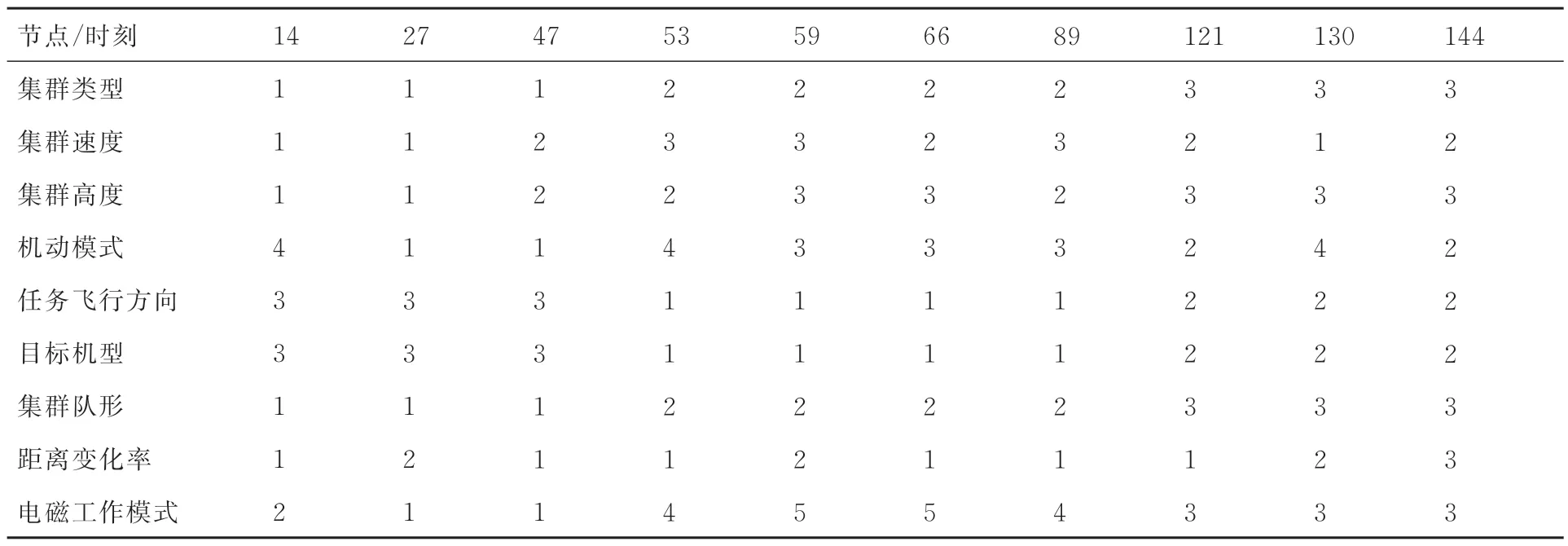
表3 训练数据具体样式Table 3 Specific style of training data

一条包含10 个时刻的训练数据总共生成每条10 个时刻的时序样本共100 条。数据样本来源于研究所给定数据特性，考虑到数据有一些偏离点或是异常值，还需要加入专家经验作为参数约束条件对模型参数进行学习，以弥补训练数据的不足。在参数约束方面，主要采集5 种类型的专家经验作为参数约束条件，主要包括：规范约束、先验约束、区间约束、同分布参数约束、0 概率参数约束。依据这5 类约束得到了的参数约束信息，以及时间序列训练样本。对图5 所示的集群编队类型的推理模型进行参数学习。

本节考虑由于模型参数较多，这里仅展示部分主要参数学习结果，分别为推理模型的集群速度条件概率表、集群高度条件概率表、集群距离变化率条件概率表等，具体如表4～表7 所示。

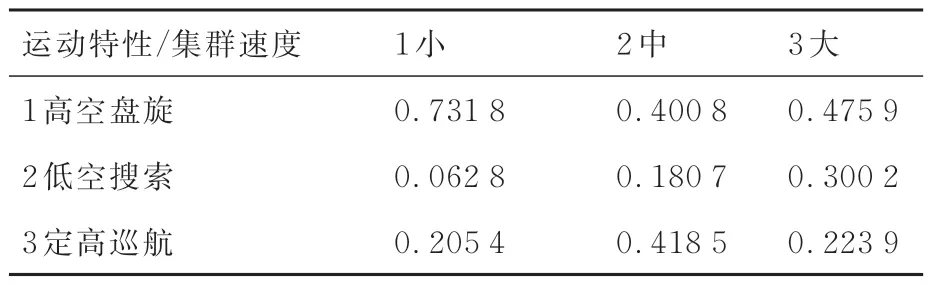
表4 集群速度条件概率Table 4 Conditional probability of cluster velocity

表5 集群高度条件概率Table 5 Conditional probability of cluster height

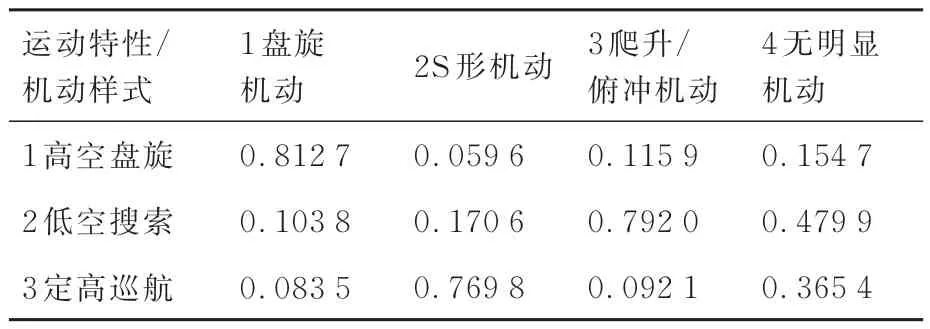
表6 机动样式条件概率Table 6 Conditional probability of maneuver

表7 雷达工作模式条件概率Table 7 Conditional probability of radar mode

上述条件转移概率表是通过本文参数学习方法所得，本文完成参数的学习，得到了完整的动态贝叶斯网络推理网络，为验证所提框架和方法的有效性，下节给出相应的仿真验证。

3 仿真验证

为了验证算法性能，本文在典型场景下通过推理置信度和正确率两项指标进行说明，验证了所提框架和算法的有效性。

3.1 场景设置

本文仿真的场景依据研究所提供的数据特性和场景要求进行测试，集群编队包括了预警编队、压制编队、扫荡编队等典型的编队类型，且符合集群目标的实际运动特点，场景描述如图6所示。

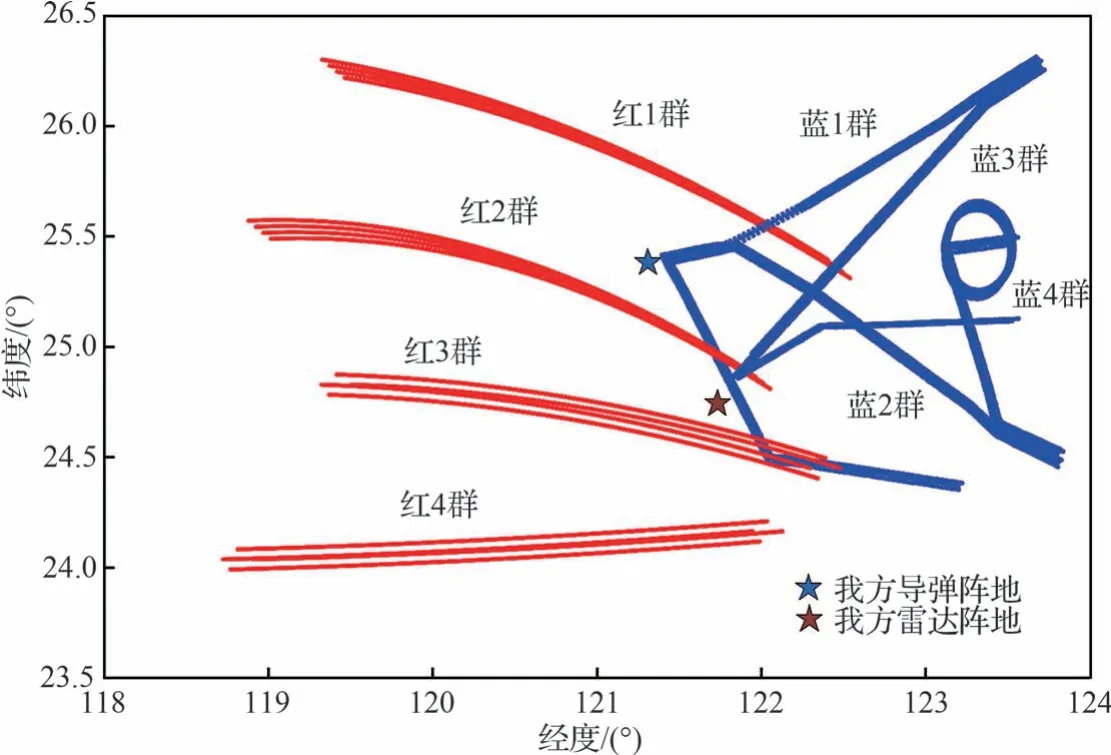
图6 任务场景下的敌我双方飞行轨迹Fig.6 Block diagram of target flight track segmentation algorithm based on two-layer segmentation

红方为我方，蓝方为敌方目标，目标主要意图是攻击中国导弹阵地和雷达阵地，目标最后分成了2 个扫荡集群，一个压制集群，一个预警集群。红方出动4 个战斗集群，并在图示区域实施拦截。由于红方4 个集群快速出击迎敌并击落2 架敌机，蓝方认为第一任务无法顺利完成，在执行任务一的过程中，预警机编队的预警机表现出一定区域盘旋机动，第一任务失败后，进而实施第二任务攻击红方某秘密基地（上图红色五角星），集群3 在靠近过程中释放干扰信号。蓝方战机在攻击红方地面目标过程中，被红方地对空导弹击落一架飞机。任务结束后，蓝方掉头撤退。

同时给出本文所设计聚类方法的关键参数：α=0.5，β=0.2，k=2，dc=4。

3.2 性能评估

本文实验是在一台联想PC 机上完成，采用64 位Windows 10 操作系统。参考文献［28］，主要以推理的置信度为主要指标进行对比，来说明本文所提算法的有效性。若有C个真实情况，无误推理次数为B次，则推理精确度为

提升程度定义为

下面给出随机参数推理算法定义［29］：不完美先验信息即先验信息不充分、不准确甚至无先验信息的情况，部分参数随机给定；经验参数定义［27，30-31］：依据先验信息对贝叶斯网络参数调整和指定。随机参数下推理结果如图7～图10 所示。

图7 随机参数下编队1 的推理情况Fig.7 Inference of Formation 1 with random parameters

由图7 和图8 可知，集群编队1 从原始位置起飞开始，考虑集群组成占比，整体集群倾向于干扰机编队，但是集群飞行目的地不明确，且推理网络参数为随机参数，总体来说此时模式不可分。第60 s 开始编队1 开始分群，分为集群编队1和集群编队3，在分群期间集群编队1 依然被识别是干扰机编队，而集群编队3 明显飞向我方高价值的雷达阵地，接近趋势愈加明显，在随机参数推理的前提下，推理结果为压制编队的置信度增大。第78 s 分群完成，集群编队1 的运动模式特征明显、飞行目的地逐渐明确，扫荡编队的置信度急剧增大，也是从此时开始，推理正确，但是整体推理准确率偏低。

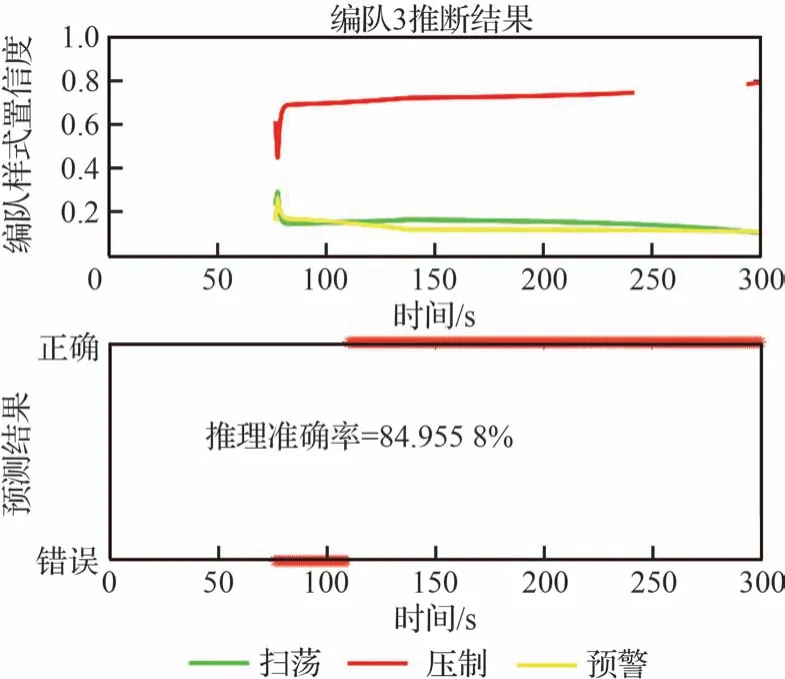
图8 随机参数下编队3 的推理情况Fig.8 Inference of Formation 3 with random parameters

编队2 起初由6 架战斗机2 架预警机组成，此时集群整体倾向识别为预警机编队，但是由于飞行目的地明确为我方重要阵地，且飞行速度快，运动属性表现为扫荡编队特性，但是由于网络参数并未反映出模型实际情况，整体集群模式不可分。直到分群结束，集群编队表现出俯冲和加速的机动模式，飞行目的地明确，特征综合分析之后，编队更符合扫荡编队特性，结果对应图9。

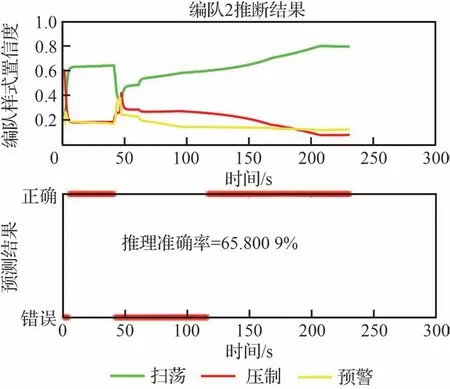
图9 随机参数下编队2 的推理情况Fig.9 Inference of Formation 2 with random parameters

集群编队4 由集群编队2 在第48 s 完全分离，从不同特性分析，集群编队表现出飞行高度大，速度慢，加之任务特性和机动模式表现出预警编队特有的机动形式，此时推理为预警编队，结果对应图10。

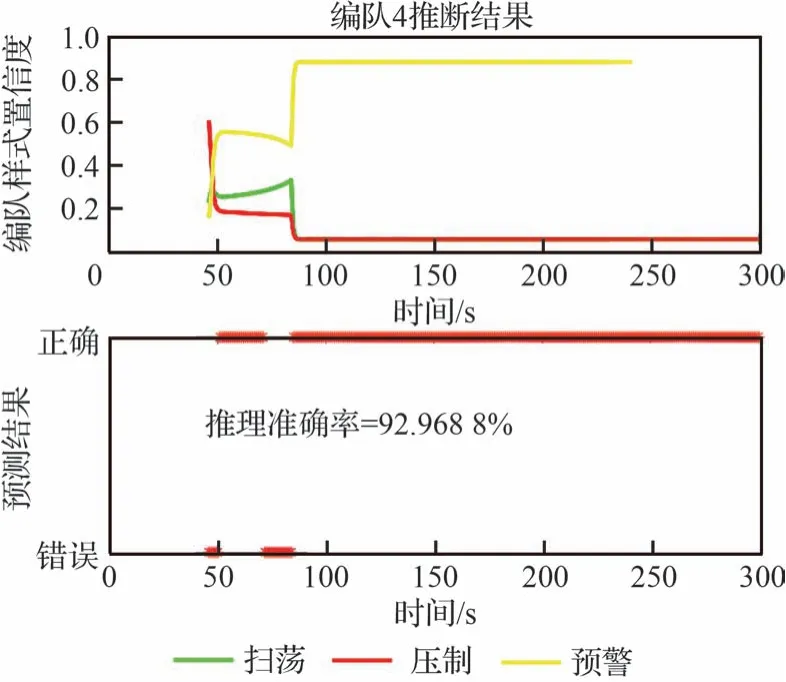
图10 随机参数下编队4 的推理情况Fig.10 Inference of Formation 4 with random parameters

此外，本文又与经验参数推理方法进行了对比，节点参数估计相比随机参数方法较准确，因此经验参数的推理结果优于随机参数的集群推理，推理的准确率平均提升了10%以上。为进一步说明方法的有效性，与文献［21］采用的多实体分层模型推理方法进行对比，仿真结果如图11～图14 所示。

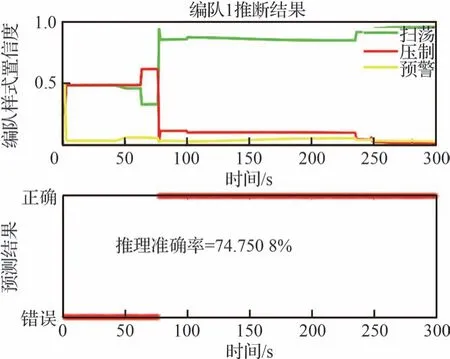
图11 多实体分层模型推理下编队1 的情况Fig.11 Formation 1 with multi-entity hierarchical inference

图12 多实体分层模型推理下编队2 的情况Fig.12 Formation 2 with multi-entity hierarchical inference

图13 多实体分层模型推理下编队3 的情况Fig.13 Formation 3 with multi-entity hierarchical inference

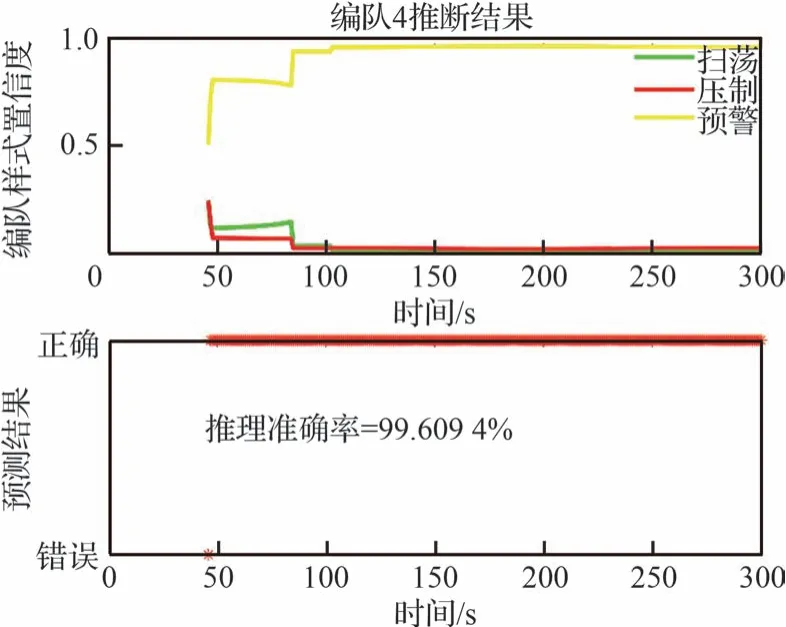
图14 多实体分层模型推理下编队4 的情况Fig.14 Formation 4 with multi-entity hierarchical inference

根据图11～图14 的仿真结果分析可知，文献［21］中设计的集群类型推理结果优于随机参数的集群推理，推理网络的参数是依据经验约束，模型参数更加准确，且从集群编队1～编队4的仿真图结果，推理准确率平均提升了6%以上。

根据图15～图16 分析可知，编队1 未出现分群动作之前，所提算法的推理结果高于其他几种算法。即使出现集群裂变/分群现象，本文所提算法推理结果的置信度依旧优于其他方法。

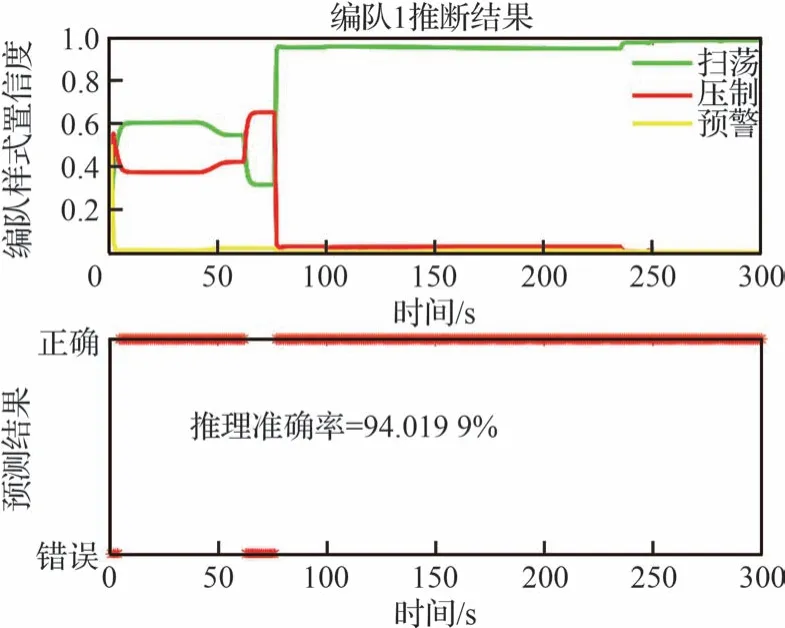
图15 参数学习下编队1 的推理情况Fig.15 Inference of Formation 1 with empirical parameters

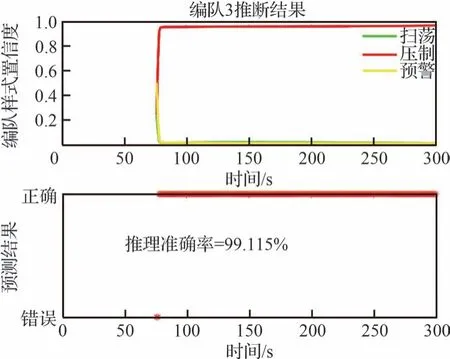
图16 参数学习下编队3 的推理情况Fig.16 Inference of Formation 3 with learning of inference network parameters

图17 参数学习下编队2 的推理情况Fig.17 Inference of Formation 2 with learning of inference network parameters

根据图15～图18 的结果分析可知，作战想定下的集群类型判断过程中，从集群编队整体飞行到执行不同任务出现分群，本文所提算法在经验参数方法和现有数据基础上，融合约束知识、模型知识等修正了专家经验知识下推理网络的参数，使集群平均识别准确占比为90%以上，置信度均高于95%。随着目标逐渐靠近，集群目标任务性明确。

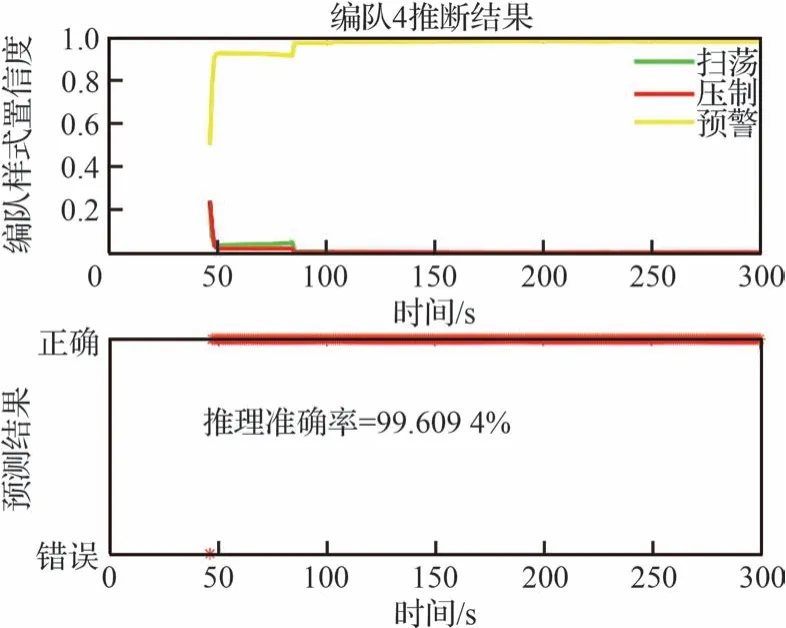
图18 参数学习下编队4 的推理情况Fig.18 Inference of formation 4 with learning of inference network parameters

此外，为有效说明目标集群涉及分析因素（速度、高度等）数据来源的有效性，图19 和图20展示标集群1 和集群2 的轨迹变化及估计值。根据图19 和图20 的目标集群的跟踪轨迹，本文获得的估计值较为准确，因此获得目标集群量测信息可以作为目标集群速度、任务方向等因素提取值的基础。综合上述，本文推理网络参数学习过后的推理识别结果又进一步得到了提高，针对上述仿真结果，将性能汇总如表8［21，29，31］所示。

表8 算法性能比较Table 8 Performance comparison of algorithms %

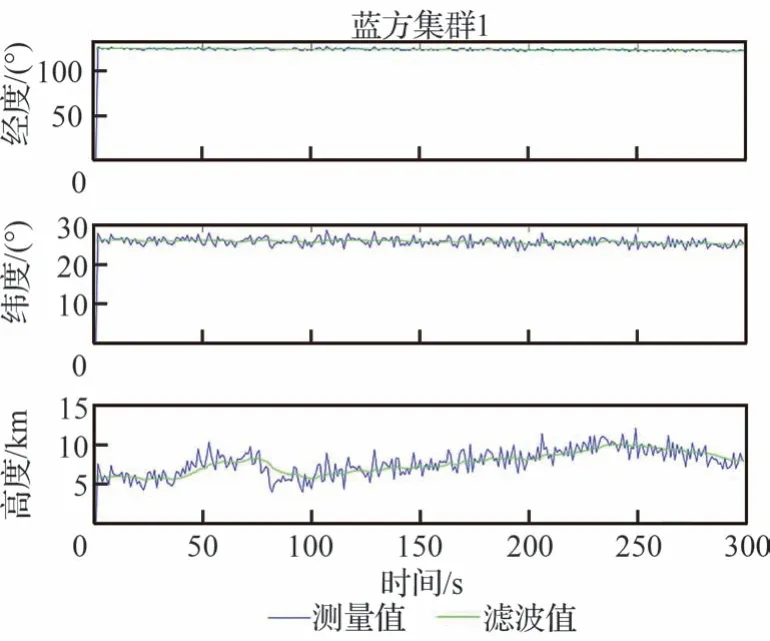
图19 目标集群1 的跟踪轨线Fig.19 Tracking trajectory of target cluster 1

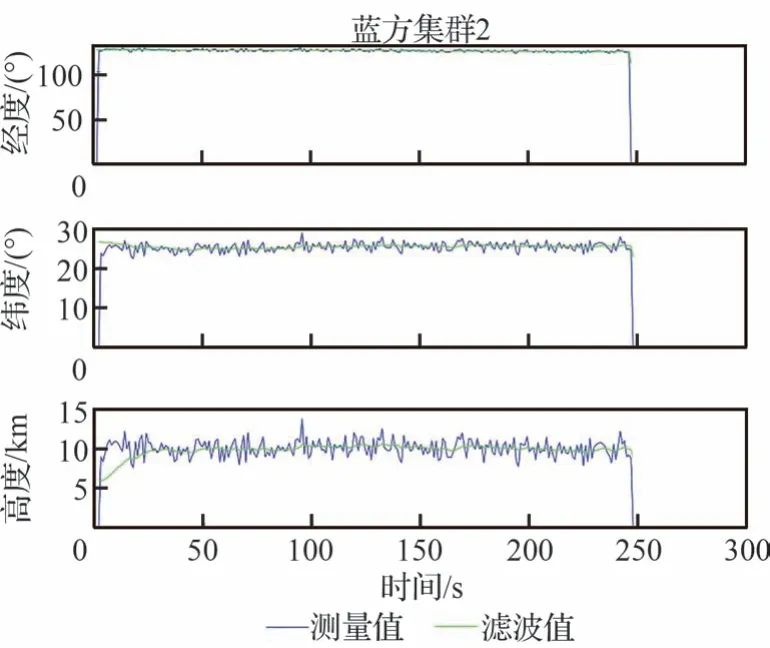
图20 目标集群2 的跟踪轨线Fig.20 Tracking trajectory of target cluster 2

对比随机参数、经验参数算法，本文方法推理准确率平均提高8%，相比文献［21］推理的结果，因为考虑了数据之间时间的相关性，集群推理准确率平均提高6%。本文所提方法得到的推理结果置信度也更高，且置信度至少提高4%。

4 结 论

本文重点研究了如何利用数据和知识进行目标集群推理问题，对集群编队作战中多种特性进行了分析，构建了分层精细化推理的集群场景识别框架。首先，预识别层检测目标运动过程中的集群的分群/合群；然后，利用知识和数据互补性，在再识别层利用所设计的动态推理网络参数学习方法，得到所需的推理网络。本文有效利用了多特征综合推理机制对目标集群进行推理分析，实现了对于集群的精细化识别，提高了集群类型识别的置信度和准确度。最后，通过典型仿真场景测试验证了所提方法的有效性。集群类型的识别是态势评估的重要因素，在未来工作中考虑在获得集群类型的基础上如何综合分析更多因素评估出整体集群作战态势变化。