考虑机场公平性的机场群航班时刻分配
水笑雨,王艳军,*,王子明,彭明田,孙强
1.南京航空航天大学 民航学院,南京 211106
2.中国民航信息网络股份有限公司,北京 101318
3.上海国际机场股份有限公司,上海 201207
随着航空运输业的持续发展,不断增长的航班时刻需求与有限可用机场资源之间的矛盾日益凸显,在一些大型枢纽机场频繁出现交通拥挤和航班延误。随着城市群的建设,相邻城市主要机场间的相互依赖性和制约性越来越强,机场群的协同运行发展已成为我国民航发展的一个重要问题。民航局在《关于进一步深化民航改革工作的意见》和《中国民用航空发展第十三个五年规划》中明确提出了建设京津冀、长三角、珠三角三大世界级机场群的目标,以北京、上海、广州等大型国际枢纽为核心整合区域机场资源,带动区域机场协调发展[1-2]。科学合理利用机场群系统资源是充分发挥机场群系统的一个关键。机场群内多个机场高度共享的空域、航段及航路点等关键空域资源成为机场群系统的一个瓶颈。如何公平、合理和有效地分配这些高度共享的空域资源已经成为一个迫切的问题。
航班时刻优化旨在对机场航班时刻资源进行合理有效分配,是机场需求和容量管理的一个重要手段,也一直是空中交通领域的研究重点。根据所研究机场数量的不同,航班时刻优化问题的研究可以分为单机场时刻优化和机场网络时刻优化两大方向。
在单机场航班时刻优化问题中,学者们主要关注在满足运行限制条件下,如何更好的满足航空公司请求时刻、合理分配机场公布容量。目前的主要优化模型使用请求偏移的概念来描述请求和分配的时刻在时间上的绝对差值,调整后的航班时刻表的总偏移代表了时刻分配的效率。Zografos 等[3]首次构建了用于解决单机场战略阶段航班时刻优化问题的整数线性规划模型。该模型在国际航空运输协会(International Air Transportaion Association, IATA)和欧盟(European Union,EU)航班时刻配置规则的基础上,考虑了机场公布容量和航班周转时间的限制,以时刻表总偏移最小化为目标,并应用于3 个希腊协调机场,大大降低了航空公司请求时刻和实际分配时刻之间的偏移量。Jacquillat 和Odoni[4]提出了一种可同时在战术和战略层面缓解机场拥堵的综合策略。通过将机场随机排队模型、机场容量利用率的动态控制模型整合到航班时刻分配的整数规划模型中,构造了战略航班时刻调配和战术机场容量利用率协同优化模型。实验证明只需要通过少量有限的时刻调整就可使航班延误显著降低。Pyrgiotis 和Odoni[5]建立了一个结合需求平滑优化模型和网络排队论模型的两阶段整数规划模型。以最小化航班总偏移量为目标,考虑联程航班周转时间的限制,同时将总体航班延误保持在尽可能低的水平,从而提高单机场容量利用率。Ribeiro 等[6]以被拒绝时刻总数量、每个航班的最大偏移量、所有航班总偏移量以及时刻调整的总数量4 个度量作为代价函数,构建了一个考虑IATA 时刻指南中一系列复杂的优先级和规定的多目标字典最小化的时刻分配模型。Zografos 等[7]构造了2 个双目标时刻协调分配模型,用以权衡时刻分配效率/偏移和时刻可接受性之间的关系。模型1 的目标为最小化总计划偏移量和最大可接受时刻偏移,模型2的目标则为最小化总计划偏移和分配在可接受时间窗之外的时刻请求的数量。结果表明,牺牲少量时刻协调效率能够有效地提高航空公司对时刻协调的可接受度。中国研究者最初是借鉴地面等待策略对航班时刻进行优化,旨在通过地面等待替代空中等待的方式降低延误带来的损失[8]。然而,单机场航班时刻优化研究不直接考虑其它机场的影响,只考虑本场运行容量和航空公司的运行要求。现行时刻协调过程中忽略了出发机场和目的地机场航班时刻的连贯性,所以优化后的网络中每个独立可行的机场航班时刻表并不意味着对整个机场网络是可行的。因此,有必要对机场网络或机场群航班时刻优化问题进行研究。
在机场网络航班时刻优化研究中,国内外研究人员通过考虑相关机场的影响,将多个机场的航班时刻优化纳入一体考虑,实现了机场网络层面航班时刻的整体优化。Castelli 等[9]提出了一个针对机场网络的整数规划模型,其目标分别为最大化可容纳航班的数量和最小化请求时刻和分配时刻的偏移。约束同时满足了机场网络内所有机场的容量限制,但该模型无法在有限时间内求出现实机场规模下的精确解。于是在2012 年,Pellegrini 等[10]采用基于迭代局部搜索和变邻域搜索的元启发式算法求解了上述模型,但是该求解方法仅适用于一天的航班时刻分配。Corolli等[11]把Zografos 等[3]提出的单机场模型拓展到机场网络层面,通过明确考虑机场容量的时变和随机性,丰富和深化了机场网络时刻调度问题。在考虑机场容量、航班连续性和周转时间等约束的情况下,提出了一个目标函数为最小化时刻表总偏移和总和预期运行延误的两阶段随机规划模型。值得注意的是,该模型假设任意一对相互连接的机场之间的飞行时间是固定不变的,并且预先知道。这样在出发地(目的地)机场分配一个时刻,相应的目的地(出发地)机场相应的时刻就被固定下来。Pellegrini 等[12]提出了一种有效的机场时刻分配同步优化的整数线性规划模型(Simultaneous Optimisation of airport SloT Allocation,SOSTA),该模型在满足现行时刻协调规章和惯例的情况下,通过周转时间约束考虑了机场网络航班中转的问题,实现了欧洲所有机场的航班时刻分配。通过与实际航班时刻协调结果对比发现,SOSTA 模型中请求的时刻数量占可接受时刻数量的比例更大。Benlic 等[13]提出了一个几乎包括所有现行规则的多机场航班时刻分配方法,包括请求优先级组、各个机场的容量约束、航班最小周转时间和航班请求系列等。该模型的规模和计算的复杂性意味着它们不能在整个调度季节中被精确地解决,文中最终采用启发式搜索算法解决了这一问题。可以看到,目前机场网络层面的航班时刻优化研究通常采用多目标优化方法实现机场网络的各个侧重点,但对机场群关键空域资源的研究较少,尤其是公平性。
然而,机场群航班时刻优化旨在解决公共空域资源潜在运行冲突,缓解机场交通拥堵,避免机场群系统航班整体计划性延误。航班时刻作为有限资源,在被分配给具有竞争利益的用户(航司/机场)时会不可避免的涉及到公平性问题[14]。Zografos 和Jiang[15]在Zografos 等[3]的模型基础上纳入了公平性,提出了一个双目标模型研究时刻表偏移和公平性的权衡问题。针对一个拥挤机场,模型分别使用ε-约束方法进行了分层和非分层求解。非分层情况下求解模型,忽略了优先级组,所有的时刻将同时进行分配。结果表明,在分层、非分层2 种情况下时刻表偏移的很小“牺牲”,将会使公平性显著提高。Zografos 和Jiang[16]构建了用于衡量各航空公司在给定时刻表中受到的公平性情况的指标。该公平性指标基于这样的原则:分配给航空公司的总时刻表偏移量的比例应该与该航司提出的请求的比例相似。然后,通过添加涉及该公平性指标的约束,将公平性纳入到时刻分配模型中。在此基础上,Zografos 和Jiang[17]满足时刻分配基本原则,构建了时刻分配效率和公平性的双目标优化模型。分配效率以航空公司请求偏移来度量,而公平性度量要求每个航空公司偏移量比较均匀,模型在分层、非分层2 种情况下对效率和公平性进行了权衡。Jacquillat 和Vaze[18]将文献[4]中提出的容量综合利用与调度模型(Integrated Capacity Utilization and Scheduling Model,ICUSM)进一步延展,新模型目标为字典最小化由各航空公司的请求数量标准化的时刻表偏移,还加入了航空公司公平性的考量,提出了基于公平性的ICUSM-E 模型,但该模型是为一天制定和求解。Fairbrother 等[19]在文献[20]的研究基础上,提出了一个结合效率、公平性和航空公司偏好的两阶段时刻分配机制,它实现了IATA WSG 的主要特征(按全航季和请求优先级调度)。第一阶段,为时刻分配定义了高峰与非高峰时段的概念,建立了新的公平性指标——基于需求的公平。这种公平性指标基于下述原则:分配给航空公司的总计划偏移的比例应该与它提出的高峰时段请求的比例相似。与前人提出的公平性指标相比,该公平性原则不会“惩罚”航司所提出的不属于高峰时段的请求。第二阶段,使用偏移预算机制实现了航司间的时刻交换。Jiang 和Zografos[21]构建了一个在容量受限机场分配航班时刻时纳入公平性的决策框架,框架主要应用一种投票方法来选择最小的机场时刻分配解决方案。其中构建了包括3 种公平性措施的双目标机场时刻分配模型,这3 种公平措施分别对应着时刻分配的3 种基于航班比例原则的公平性指标,分别为:① 最小化与绝对公平性的最大偏差(Minimise the Maximum deviation from the Absolute fairness,MMA);② 最小化与平均公平性的最大偏差(Minimise the Maximum deviation from the aveRage fairness,MMR);③ 最小化基尼指数(Minimise the Gini Index,MGI)。总的来说,虽然上述有很多研究从不同角度对公平性指标进行了描述,但大部分文献都是从航空公司的角度考虑公平性。考虑机场公平性的机场群航班时刻资源分配,鲜有相关工作开展。
机场群协同发展定位和各成员机场的资源配置关系到机场群系统的整体发展,因此,研究机场群航班时刻优化配置,公平分配和充分利用机场和空域时刻资源,有助于提高航班正常率,提升机场群运行效率。本文考虑机场群关键空域资源分配的机场公平性,提出了基于基尼系数的机场群整体公平性度量。该度量考虑了各机场在潜在离场冲突点的需求。然后,综合考虑机场容量和空域容量,提出了一个基于机场间公平性的机场群航班时刻优化模型。该模型兼顾了机场群内各成员机场的协同运行和不同机场的功能定位。最后以粤港澳大湾区五机场实际航班数据为例展开实例分析,验证了模型的有效性和可扩展性。
1 问题描述
2011 年,Clarke 等[22]研究了美国4 个主要机场群,确定了多机场运行相关的12 个主要问题。其中影响机场群运行最大的3 个问题分别是:共用的离场航路点、区域内共用空域的管理和临近机场配置产生的运行冲突。本文针对机场群中各成员机场在共用离场航路点的时刻资源的公平分配进行研究。
考虑离场航路点资源分配机场公平性的航班时刻分配问题可以被简述为:在满足机场群内各成员机场的公布容量、机场终端区内关键航路点容量的前提下,考虑航班在机场群空域内的飞行时间、周转时间等约束,确定每个航班的起降时刻,使得优化后的航班时刻与航空公司申请时刻的总偏移最小,且机场之间在离场点公平性最好。
作出如下假设:
1) 航班时刻不是一个精确、具体的时间点,而是一段特定时间区间长度的时间段。同一机场最小时刻的长度相同,通常设定为5 min。机场的公布容量(或时刻容量)规定了一天中某一时间段内最多可以起降航班的架次。通常机场的公布容量可以定义为15 min 容量和60 min 容量。
2) 航班时刻优化问题面向战略流量管理,因此仅考虑正班航班,不考虑加班、包机、取消航班等情况。
3) 周转时间是指前序航班到场之后、后序航班离场之前的时间间隔。联程航班的实际周转时间必须介于最大周转时间和最小周转时间之间。联程航班必须保证有充足的时间上下客和进行地面保障服务。本文对联程航班设定统一的最大最小周转时间,后续模型可以考虑机型、国际/国内航班设置周转时间。
4) 仅考虑目标机场群内的机场航班,不考虑其在该机场群外的机场的航班起降时刻及周转时间。
5) 假定航班在机场群内各机场到关键空域点(包括离场航路点)之间的飞行时间为固定值,并选取历史飞行时间数据的中位数作为机场和航路点之间的飞行时间。后续研究工作可考虑飞行时间不确定性的影响。
6) 以机场群内航空公司的现行时刻表作为时刻申请,并认为各航司所能接受的航班最大偏移量相同。
2 机场群航班时刻优化公平性模型
2.1 决策变量
模型的决策变量为
式中:a∈A,A={1,2,…,|A|+1}为机场集合,|A|为机场群内机场的总数,而|A|+1 代表一个虚拟机场,包括时刻表中除机场群以外的所有机场;t∈T,T={1,2,…,|T|}为以5 min 为时间区间长度的时间段的集合;m∈M,M为机场群内所有航班的集合。
为了标识机场群中某个机场的航班申请是否属于离场航路点上的一个高峰时段(刻),引入另一个0-1 变量,如式(2)所示:
式中:u为机场群内的一个离场航路点,u∈U,U={1,2,…,|U|}为机场群内所有离场航路点的集合;t'为航班请求m在离场航路点u实际被分配的时刻,t'的值等于时刻t加上航班请求m到离场航路点u的飞行时间。
2.2 优化目标
目标1最小化机场群内所有航班时刻申请的总偏移
综合考虑机场群中各机场容量和空域容量约束,优化航班时刻,使得机场群内各机场航班时刻表中总的航班偏移量最小,即
式中:tm为时刻表中航班m计划申请的时刻;t为航班请求m实际被分配的时刻;|t-tm|为航班m时刻申请与实际分配之间的差值的绝对值,即时刻偏移量。
目标2最小化航班最大偏移量
考虑各航司所能接受的航班最大偏移量相同,一般情况下航班最大偏移量越小,航司对时刻表的接受度越高,即
式中:tmax=max|t-tm|为单个航班的最大允许偏移量。
目标3最小化机场群中机场公平性的整体度量
将Fairbrother 等[19]提出的高峰请求比例原则拓展到机场群层面:机场群内的某一机场的航班在一个拥堵的离场航路点所获得的航班偏移量与所有机场在该点的总偏移的比值,应该与其在该离场航路点的高峰时刻占比相等。定义基于高峰需求的机场公平性指标为
式中:μa,u表示机场群中a机场在共用离场航路点u上,基于高峰需求的机场公平性指标,μa,u=1 代表机场a在离场航路点u被公平对待,0 ≤μa,u<1 代表机场a在离场航路点u被优待,μa,u>1 代表机场a在离场航路点u被不公平对待;Sa,u为机场a申请的航班在离场航路点u的时刻偏移量;Su为机场群内各机场的所有航班在离场航路点u的时刻偏移量;ra,u为机场a的高峰时刻航班数量在机场群中离场航路点u上的占比,所谓“高峰时刻航班”即处于高峰时段的航班,下文会详述。
Sa,u、Su和ra,u分别为
式中:Ma,u为机场a中所有经过离场航路点u的航班集合;Mu为机场群内所有经过离场航路点u的航班集合;Na,u为机场a申请的航班在离场航路点u是高峰时刻航班的数量;Nu为机场群内各机场所申请航班在离场航路点u是高峰时刻航班的数量。
Na,u、Nu可分别由高峰时段决策变量计算得到:
μa,u只能单独评价机场a在离场航路点u的公平性,对于机场群系统而言,考虑机场公平性整体度量时如果仅对μa,u求和取最小值,则缺少合理性。本文引入基尼系数,它最早由意大利统计学家基尼于1912 年提出,是衡量一个国家居民收入分配的经典经济指标[23]。基于基尼系数概念的新度量能较好地表征机场群系统在离场航路点u的公平性。由此,关于机场群中机场公平性整体度量的目标函数为
式中:|A|为机场群内机场的总数,不包括虚拟机场|A|+1;μi,u、μj,u分别表示机场群内第i、j个机场在离场航路点u的公平性指标,i∈A,j∈A;Gu为高峰请求比例原则下,基于基尼系数的离场航路点u上的机场公平性整体度量。
2.3 约束条件
约束1每个航班请求在机场群内同一个机场只能分配一个时刻,即
约束2联程航班需要满足最小、最大周转时间约束,即
约束3机场进场、离场、总容量约束
式(14)和式(15)分别表示机场a在15、60 min时,其进场、离场、总容量约束。
式中:K={Arr,Dep,Total}为航班运行类型的集合,包括进场、离场、总和3 种运行类型,由k索引;Mk为机场群内所有运行类型为k的航班集合,MArr∪MDep=MTotal;Ma为机场a申请的航班集合,a∈A;为机场a申请的所有运行类型为k的航班集合;t∈T,T={1,2,…,|T|}为以5 min 为时间区间长度的时间段的集合;tq∈TQ,TQ={1,2,…,|TQ|}为以15 min 为时间区间长度的时间段的集合,以tq索引;th∈TH,TH={1,2,…,|TH|}为以60 min 为时间区间长度的时间段的集合,以th索引分别为航班运行类型为k的机场a在15、60 min 时,其机场容量。
约束4航路点容量约束
式(16)和式(17)分别保证了优化后的航班满足进场航路点的15、60 min 容量约束;式(18)和式(19)分别保证了优化后的航班满足离场航路点的15、60 min 容量约束;而式(20)和式(21)分别保证了优化后的航班满足同时存在进场和离场航班的航路点的15 和60 min 容量约束。
进场航路点:
离场航路点:
同时存在进离场航班的航路点:
式中:Fix={1,2,…,W}为机场群内所有航路点的集合为使用进场航路点w的航班集合,为使用离场航路点w的航班集合;为航班m从进场航路点w飞行到机场a的飞行时间,为航班m从机场a飞行到离场航路点w的飞行时间;为航路点w在航班运行类型为k时,15 min 时间段内能够通行的航班数量,k∈K={Arr,Dep,Total};为航路点w在航班运行类型为k时,60 min 时间段内能够通行的航班数量,k∈K。
2.4 模型求解
本文研究主要考虑机场群内所有航班时刻申请总偏移的最小化。为此,在模型求解过程中,将最小化航班最大偏移量和最小化机场群中机场公平性的整体度量的这2 个目标转化为新的约束条件,并加入模型当中。
1) 目标2:最小化航班最大偏移量,转化为每个航班必须满足的最大偏移量约束,即
式中:tmax为航班的最大允许偏移量。式(22)表示每个航班在时刻分配的过程中有一个最大允许偏移量,为各航空公司所接受。
2) 目标3:最小化机场群中机场公平性的整体度量。转化为基于高峰需求的整体公平性约束,即
式中:Gu为高峰请求比例原则下,基于基尼系数的离场航路点u上的机场公平性整体度量,也可称为基于高峰需求的基尼机场公平性;ε为机场群在航路点上机场公平性整体度量的上界,也可称为可接受的机场公平性度量。根据基尼系数的自然范围,ε∈[0,1],ε的具体数值可由机场群中各机场的时刻协调员商定。
同理,为了进行时刻表分配结果的对比,参考Zografos 和Jiang[15]给出非基于需求的机场公平性指标,即基于航班比例的机场公平性:机场群内的某一个机场的航班在一个拥堵的离场航路点所获得的航班偏移量与所有机场的总偏移的比值,应该与其在该离场航路点申请的航班数量占比相等。定义非基于需求的机场公平性指标为
式中:ρa,u的定义解释跟上述μa,u类似,表示机场群中a机场在共用离场航路点u上,非基于需求的机场公平性指标,ρa,u=1 代表机场a在离场航路点u被公平对待,0 ≤ρa,u<1 代表机场a在离场航路点u被优待,ρa,u>1 代表机场a在离场航路点u被不公平对待;Fa,u为a机场申请的,并经过离场航路点u的航班的数量;Fu为机场群内各机场经过离场航路点u的所有航班的数量。
相似地,可以得到非基于需求的整体公平性约束,即
航班时刻优化是一个约束求解十分复杂的难题。文中该问题求解过程在Windows10 操作系统下进行, 应用Python 3.8.5进行编程, 所使用的求解器为Gurobi 9.1.1,所用设备的内存为16 GB,四核Inte(lR)i7-4790 CPU, 频率为3.6 GHz。
3 实例分析
本文以粤港澳大湾区机场群为研究对象,对广州白云国际机场(ZGGG)、深圳宝安国际机场(ZGSZ)、珠海金湾国际机场(ZGSD)、澳门国际机场(VMMC)和惠州平潭机场(ZGHZ)所构成的机场群系统进行航班时刻整体优化。其中,括号中字母缩写为国际民航组织四字机场代码。需要说明的是,因中国香港国际机场(VHHH)目前的航班运行与中国内地上述机场运行相互隔离,因此暂未考虑香港国际机场。图1 为粤港澳大湾区机场群航班运行的示意图。其中,灰线划定了机场群所在终端区(广州和珠海进近管制区)的边界,其他不同颜色的线表示不同机场的进离场航路。

图1 粤港澳大湾区机场群空域图Fig.1 Airspace of multi-airport system in Guangdong-Hong Kong-Macao Greater Bay Area
3.1 模型参数设置
本文实例数据来源于2018—2019 年大湾区五机场的历史运行数据和2019-12-21 五机场单日的航班时刻表数据。数据包括航班号、飞机注册号、机型、起飞机场、着陆机场、计划起飞时间、实际起飞时间、计划着陆时间、实际着陆时间。
1) 机场群中各机场和关键航路点的公布容量。
大湾区机场群内各机场的公布容量由空中交通管制单位提供,如表1 所示。模型中的关键航路点及其容量则由空中管制员根据经验给出。所谓航路点是指航路上用于定义各航段的地理位置点,或航空器航线飞行时所参照的地理位置点,一般以英文标识。本文考虑的关键航路点包括GYA(高要)、LMN(龙门)、MIPAG、NOLON、OVGOT、TEPID、VIPAP 和YIN(英德)等,如表2 所示,各机场在YIN 航路点的航班请求数量如表3所示。

表1 机场公布容量Table 1 Airport declared capacity

表2 关键航路点容量Table 2 Critical fix capacity

表3 各机场在YIN 航路点的航班请求数量Table 3 Number of flight requests by each airport at YIN
2) 公平性建模对象
结合图1 和表3 可知:五机场在YIN 航路点航班量密集,且只作为共用离场点使用。所以,本实例拟以共用离场点YIN 作为机场公平性的主要建模对象。
3) 飞行时间
模型并未考虑飞行时间可变,航班在机场和航路点之间的飞行时间设置为2018—2019 年历史飞行时间的中位数。
4) 航班最大偏移量/调整量
为了尽可能保证单个航班的公平性,或者说相对航空公司的公平性,航班的最大偏移量/调整量tmax设置为10 min。
5) 高峰时刻的定义
以15 min 为时间区间长度的某个时刻,如果某个离场航路点15 min 内分配到该时刻的航班量大于等于该点的15 min 航班参考容量,那么就称该时刻为一个高峰时刻,分配到这个时刻内的航班将被称为高峰时刻航班。此时,高峰时刻指标为否则
6) 机场公平性度量参数
由于基尼系数的自然取值范围为[0,1],首先把可接受的机场公平性度量参数ε设置为[0,0.1),[0.1,0.2),…,[0.8,0.9),[0.9,1.0]10 个取值区间,然后在整体公平性约束的两端分别设置(ε1,ε2)∈ε进行范围约束,最后分别对每个区间采用逐次的二分法求得最小的目标值。有一点说明:无论是基于高峰需求还是非基于需求的机场公平性方法,2 种方法的机场公平性整体度量Gu和Gu',在模型中都是由基尼系数公式计算而来,所以均可统称为基尼机场公平性,也可分别称为基于高峰需求的基尼机场公平性和非基于需求的基尼机场公平性。
7) 优化求解器参数
为求解所提出的非线性机场整体公平性约束,将Gurobi 的NonConvex 参数设置为2。
3.2 优化结果与分析
3.2.1 基于高峰需求与非基于需求的机场公平性方法对比
1) 时刻表总偏移与基尼机场公平性的权衡
图2 为时刻表总偏移与基尼机场公平性的有效边界。为了便于比较,参考文献[16]计算了时刻表总偏移与非基于需求的基尼机场公平性的有效边界。3 幅子图分别为基尼机场公平性取值为[0.35,0.50]、[0.50,0.65]、[0.65,0.80]区间时的缩放图,分别用箭头指示了2 条曲线的交点的坐标。基尼系数可以表征资源分配的整体公平性,其取值在[0,0.4]区间内对各利益相关方均是相对公平的。对于时刻资源分配来说,“基尼系数”(也就是基尼机场公平性/机场公平性整体度量)的值越小,机场群总体时刻表越公平。

图2 时刻表总偏移与基尼机场公平性的有效边界Fig.2 Total displacements of schedule and efficient frontiers of Gini airport fairness
由图2 可知,基于高峰需求的基尼机场公平性与时刻表总偏移的权衡效果比非基于需求的基尼机场公平性更好;同时,图2 也表明了可以在一个机场群中共用离场航路点上构建对各机场的时刻分配都更加公平的总体时刻表,而且只会导致航班总偏移很小的增加。从右侧缩放图可以看出,在离场点基尼机场公平性取值大约0.39之前,非基于需求的机场公平性方法对应的时刻表总偏移都在基于高峰需求的机场公平性方法之上。这实际上再次说明了,在[0,0.39]的整体公平性较好范围内,基于高峰需求的基尼机场公平性与时刻表总偏移的权衡效果更好。另外,基尼机场公平性在大约[0.39,0.71]区间内,2 种基尼机场公平性与总偏移权衡关系的“好坏”存在反复,但对应时刻表总偏移的差距不大。而且,根据基尼系数的定义,基尼机场公平性>0.4 的情况下,总体时刻分配已属于“比较不公平”的状态。因此,没有必要在该范围内继续划定2 种基尼机场公平性与总偏移的权衡关系“好坏”。值得注意的是,基尼机场公平性在[0.71,0.80]范围内增加时,2 种机场公平性方法下的总偏移都显著升高,但非基于需求方法对应的曲线敏感性更高,增大趋势更明显。
2) 离场航路点YIN 的航班时刻总偏移与基尼机场公平性的权衡
图3(a)和图3(b)分别为基于高峰需求和非基于需求的机场公平性方法下,YIN 航路点航班时刻总偏移与基尼机场公平性的有效边界。为突出和对比,加入了对应的时刻表总偏移的变化曲线。图中红色点划线代表有效解和无解的近似分界线:基尼机场公平性取值>0.8,模型不存在可行解。由图3(b)可知,在非基于需求的机场公平性方法下,当基尼机场公平性取值为0(即绝对公平)时,总偏移达到最大值2 360 min,对取值区间多次二分法求解最小目标值,最终得到:模型存在有效解的基尼机场公平性取值范围大约为[0,0.793 2]。因为“绝对公平”的特殊性,其要求严格按照航班时刻请求比例分配相应的偏移量。所以,曲线整体趋势在达到最大偏移量2 360 min 后陡降,之后偏移量持续波动在平均360 min 左右。在基尼机场公平性取值0.71 左右开始急剧上升,直至在大约0.793 2 左右取得最后的有效解,偏移量为1 800 min;而由图3(a)可知,基于高峰需求的机场公平性方法下,存在有效解的基尼机场公平性取值范围为[0,0.795]。整体趋势上大部分区间的偏移量平稳波动在345 min 左右,在基尼机场公平性取值0.726 左右开始陡升,直至升至偏移量1 730 min,但升高的剧烈趋势同样不如非基于需求的机场公平性的情况。
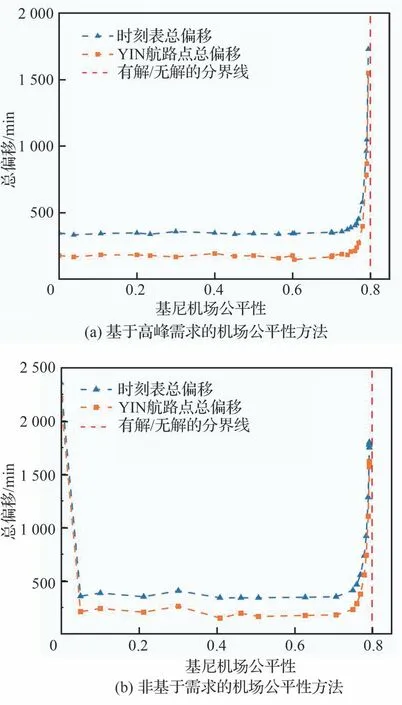
图3 离场点YIN 航班时刻总偏移与基尼机场公平性的权衡Fig.3 Trade-off between flight displacements at YIN and Gini airport fairness
值得注意的是,在离场航路点YIN,同样也是基于高峰需求的基尼机场公平性与总偏移达到了更好的权衡。这是因为,模型的基尼机场公平性的约束建立在离场航路点YIN 上,所以从因果关系上看,基于高峰需求的基尼机场公平性与YIN 点航班总偏移的更好权衡“贡献”了它与时刻表总偏移的更好权衡。虽然离场点YIN 的航班流量大,但这种“贡献”程度是否巨大目前并不能预知。为此,以下将研究未通过YIN 点的航班总偏移与2 种基尼机场公平性的权衡关系。这里将机场群中不通过YIN 航路点的所有航班的总偏移定义为“航班偏移差值”。
3) 航班偏移差值与基尼机场公平性的权衡
图4 为航班偏移差值与2 种基尼机场公平性的权衡关系。由图4 可知,基于高峰需求的机场公平性方法与非基于需求的方法相比,航班偏移差值的上下波动范围更小也更稳定。这说明基于高峰需求的机场公平性方法对于机场群内不通过YIN 航路点的航班的整体影响是相对稳定的。但是,当基尼机场公平性取值[0,0.36]的“相对公平”区间时,非基于需求的基尼机场公平性与航班偏移差值的权衡比基于高峰需求的基尼机场公平性更好。这与上述时刻表总偏移和YIN 总偏移的对应结论相反。这是因为,模型本身要求目标函数为时刻表总偏移最小化,所以可能以“牺牲”不通过YIN 点的航班的偏移量的方式实现。非基于需求的机场公平性方法要求严格按照航班比例原则分配航班偏移,又因为模型中不允许拒绝航班请求,所以该方法对航班偏移差值的影响是有限的;但基于高峰需求的机场公平性方法关注高峰时段内航班偏移的分配,由于时空的连续性和航空网络的传播性,某一航路点的航班被偏移必然影响与之相关的机场群中不通过YIN 航路点的所有航班的时刻偏移,即航班偏移差值,且这一影响视问题复杂度是可叠加的。另外,随着基尼机场公平性取值在大约0.765 之后,航班偏移差值稳定在180 min。这在一定程度上说明:在0.765 左右的极不公平情况下,无论在YIN 航路点构建哪种基尼机场公平性约束,对于机场群内其他航班偏移量的影响可能是相同的。这可能与当前模型中不允许拒绝航班请求以及航班最大偏移约束有关,从而导致YIN 航路点基尼机场公平性约束对航班偏移差值的影响达到“极限”,趋向于稳定。

图4 航班偏移差值与基尼机场公平性的权衡Fig.4 Trade-off between flight displacement difference and Gini airport fairness
4) 机场群中各机场相关参数与基尼机场公平性的权衡
图5 为2 种基尼机场公平性下,机场群内各机场在离场点YIN 的机场公平性指标变化情况。由图5 可知,在2 种机场公平性方法下,当基尼机场公平性取值[0,0.4]的整体“相对公平”区间时,ZGSZ、ZGSD、ZGHZ 和VMMC 这4 个机场的机场公平性指标均≤1,而且随着基尼机场公平性的增加都逐渐减少到0;而ZGGG 机场在2 种方法下的机场公平性指标均≥1,对应的机场公平性指标随着基尼机场公平性的增加从1 开始分别达到2.64、3.44 的峰值。根据机场公平性指标的定义,ZGSZ、ZGSD、ZGHZ 和VMMC 这4 个机场在YIN 航路点时刻资源分配方面被优待,而ZGGG 机场则处于劣势地位。由表3 可知,ZGGG 和ZGSZ 两机场在YIN 的总航班量占YIN 点航班量的84%左右。有趣的是,在ZGGG经过YIN 的航班量明显少于ZGSZ 的情况下,ZGGG 的机场公平性指标却大于等于ZGSZ,这说明ZGGG 相对地“承担”了更多的航班时刻偏移。为了解释出现这一现象的合理性,下面将研究各机场在离场点YIN 的所获偏移量占比和高峰时刻航班的数量。
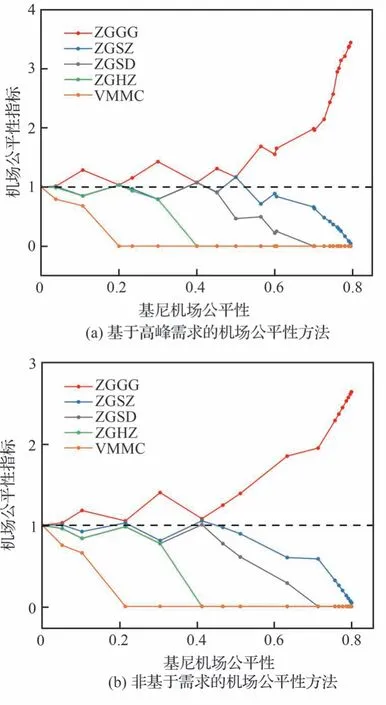
图5 各机场在YIN 航路点的公平性指标Fig.5 Fairness index for each airport at YIN
图6 为机场群内各机场在离场点YIN 所获偏移量占YIN 总偏移的比例(简称为所获偏移量占比)随2 种基尼机场公平性的变化情况。由图6可知,对于2 种基尼机场公平性,各机场所获偏移量占比的整体变化趋势是基本相似的。ZGGG所获偏移量的占比逐渐增加,最终趋近于1,显然YIN 点时刻分配结果对ZGGG 机场最不公平;ZGSZ 所获偏移量的占比由47%逐渐下降,最后趋近于0;ZGSD、ZGHZ 和VMMC 所获总偏移量从最初14%左右减少为0,公平性指标≤1,三机场在时刻资源分配上被优待。另外,由图6 可知,ZGGG 与ZGSZ 的所获偏移量占比在[0,0.4]的相对公平区间内呈现一种近似相互牵制的状态,这可能和两机场在YIN 的航班数量相近有关。在非基于需求的机场公平性方法下,在基尼机场公平性取值[0,0.25]范围内,ZGGG 的偏移占比小于ZGSZ,这显然遵循按照航班请求数量分配偏移量的原则。但基于高峰需求的机场公平性方法下,相同的基尼机场公平性取值范围内,ZGGG 的偏移占比与ZGSZ 在大小关系上存在明显的反复。
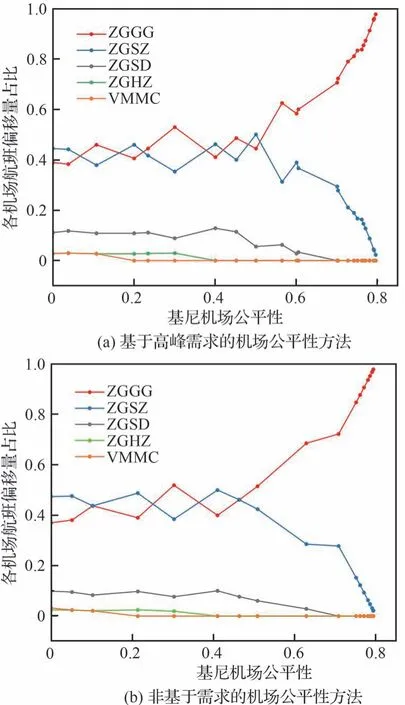
图6 各机场航班所获偏移量占YIN 点航班总偏移的比例Fig.6 Proportion of flight displacements obtained by each airport to total flight displacements at YIN
图7 为2 种基尼机场公平性下,机场群内各机场在离场点YIN 的高峰时刻航班数量的变化情况。结合图7 并查看ZGGG 和ZGSZ 机场通过YIN 航路点的时刻请求的数据。可以看到,ZGGG机场虽然航班数量明显少于ZGSZ,但是航班请求的时刻大多集中在早中晚的“黄金时段”,与之相比,ZGSZ 机场请求的时刻很多都分布在一天中的深夜和凌晨时段。这种时刻需求的分布情况直接导致ZGGG 机场比ZGSZ 更容易获得最多的航班偏移量。在2 种机场公平性方法下,尤其是基于高峰需求的方法,其设定的高峰请求比例原则对高峰航班请求敏感,它会进一步权衡高峰请求数量和航班偏移的关系:针对高峰时段需求,模型会通过增减高峰航班数量的方式调整相应的航班偏移量,如图7所示。另外,如图6所示,当基尼机场公平性取值[0,0.25]范围内,ZGGG 的偏移占比与ZGSZ 在大小关系上存在多次的反复和权衡,也说明了这种高峰时段航班调节作用的存在。而非基于需求的公平性方法则凭借航班数量来“分摊”航班偏移,但这间接地惩罚了不在高峰时段内的航班,不能体现航班层面的公平性。

图7 各机场在YIN 航路点的高峰时刻航班数量Fig.7 Number of peak-period flights by each airport at YIN
3.2.2 最小总偏移下时刻分配结果分析
图8 为模型目标取得最小时刻表总偏移时,机场群内各机场在离场点YIN 的机场公平性指标的柱形图。图中包括以下3 种情况,如表4 所示:基于高峰需求的机场公平性方法,基尼机场公平性取值0.037 7(简称基于高峰需求方法(0.037 7)),对应于时刻表总偏移最小;非基于需求的机场公平性方法,基尼机场公平性取值0.409 4(简称非基于需求方法(0.409 4)),对应于时刻表总偏移最小;非基于需求的机场公平性方法,基尼机场公平性取值0.050 8(简称非基于需求方法(0.050 8)),对应时刻表总偏移为355 min,仅用作对比分析。图8 中取值1.0 的水平点划线为机场在时刻资源分配中被公平对待时的公平性指标参考基准。

表4 2 种机场公平性方法下的最小时刻表总偏移Table 4 Minimum total schedule displacement obtaiend with two different airport fairness methods
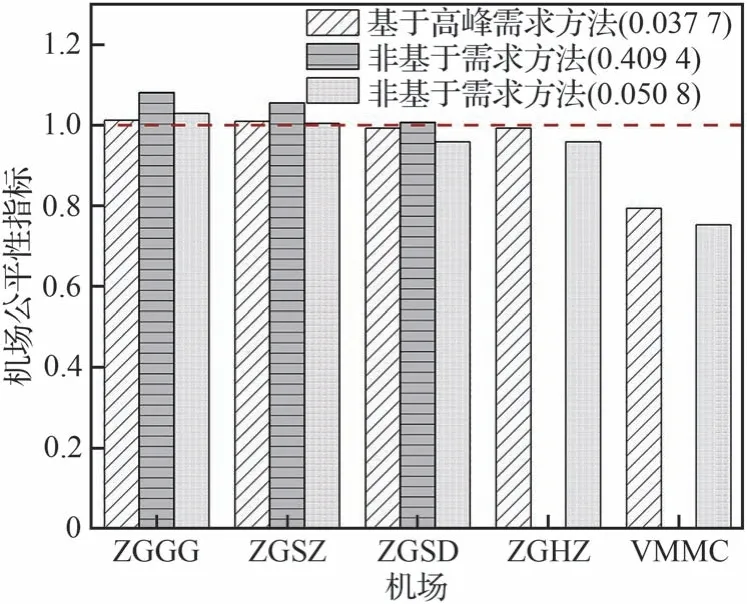
图8 最小时刻表总偏移下五机场的机场公平性指标Fig.8 Airport fairness indices of five airports with the minimum total schedule displacements
由图8 可见,基于高峰需求方法(0.037 7)下的模型目标—时刻表最小总偏移量为335 min,除VMMC 外的各机场公平性指标均接近于1。这说明YIN 航路点上航班时刻请求的偏移量分配对除VMMC 外的各机场都相对公平,而VMMC 被一定程度上优待。同时,与非基于需求方法(0.409 4)相比,基于高峰需求方法(0.037 7)在YIN 点的基尼机场公平性取值更小,即机场群在YIN 点的整体机场公平性更好;非基于需求方法(0.409 4)下,虽然ZGGG、ZGSZ、ZGSD 的机场公平性指标均大于且接近于1,但ZGHZ 和VMMC 机场公平性指标为0,这表明ZGHZ 和VMMC 的航班没有被偏移,两机场在时刻偏移分配的过程中被优待。从机场群系统角度来说,这对于ZGGG、ZGSZ、ZGSD 三大机场是不公平的,该结果主要是牺牲了ZGGG和ZGSZ 的机场公平性换来的。
此外,非基于需求方法(0.050 8)下,除VMMC 的机场公平性指标为0.75 左右,所以其在航班偏移量分配中被优待以外,其余四机场的公平性指标均接近于1,处于相对公平地位。所以非基于需求方法(0.050 8)与非基于需求方法(0.409 4)相比,在YIN 航路点所产生的时刻分配结果的机场群整体公平性更好。结合表4 所示,与非基于需求方法(0.409 4)相比,虽然非基于需求方法(0.050 8)的情况下,最小时刻表总偏移增加了15 min,但是对应的基尼机场公平性却从0.409 4 减少到0.050 8,在YIN 航路点的机场群整体公平性大大改善。这表明,在非基于需求的公平性方法中,可能会通过牺牲机场群中部分机场的公平性的方式取得整体公平性的提高。基于高峰需求的机场公平性方法则会兼顾机场群中各机场在关键航路点的时刻需求。这也侧面反映出,模型在针对时刻表总偏移进行单目标优化时,非基于需求的基尼机场公平性与总偏移的权衡效果不佳。
图9 为基于高峰需求方法(0.037 7)和非基于需求方法(0.409 4)情况下,机场群经过离场点YIN 的15 min 航班量日变化。其中红色水平线指向纵轴数值9,代表YIN 航路点的15 min 航班容量约束为9 架次。由图9 可知,与YIN 航路点计划航班架次相比,被2 种机场公平性方法优化调整后的每15 min 的离场航班架次分布都更加均衡且满足航路点容量限制,航班时刻优化达到了“削峰填谷”的效果。而且,基于高峰需求方法(0.037 7)和非基于需求方法(0.409 4)情况下,调整后的YIN 点高峰时段的分布是相同的。高峰时段包括:8:00—8:15,8:30—8:45,8:45—9:00,9:00—9:15,9:15—9:30,9:30—9:45,9:45—10:00,10:15—10:30,11:45—12:00,12:30—12:45,13:30—13:45,15:45—16:00,16:00—16:15,17:15—17:30,21:15—21:30。这些时段都是航班请求的“黄金时段”,具有较高的时刻价值。值得注意的是,与非基于需求方法(0.409 4)相比,基于高峰需求方法(0.037 7)产生的航班时刻分配结果在13:45—14:30,17:45—18:30,21:45—22:30 等3 个非高峰时段均做了航班架次的调整,使得航班时刻的需求分布均向后移动,航班分布更加均匀平滑。这可能是航路点本身容量约束的缘故。

图9 基于高峰需求方法(0.037 7)和非基于需求方法(0.409 4)下,通过离场点YIN 的15 min 航班量Fig.9 Number of flights per 15 min through YIN obtained with the peak demand-based fairness method (0.037 7) and the non-demand-based fairness method( 0.409 4)
图10 为非基于需求方法(0.409 4)和非基于需求方法(0.050 8)情况下,机场群经过离场点YIN 的15 min 航班量日变化。由图10 可知,非基于需求方法(0.050 8)调整后的15 min 航班分布比非基于需求方法(0.409 4)更加均匀,相邻15 min 时间段内航班架次突增的现象愈加减少。结合图9 和图10,可以看出:在离场航路点YIN,无论是基于何种机场公平性方法分配航班偏移量,更小的基尼机场公平性取值,也就是更好的整体公平性,往往意味着调整后的航路点航班分布更均匀平滑。另外,依照15 min 的高峰时段定义,虽然航班计划中一些时段没有超出当时的最大航路点容量,但其可能是潜在冲破容量约束的时段,也就是说,在实际运行突发和多变的情形下,这些时段容量约束最有可能首先被突破,尤其是那些高峰时段的邻近时段,例如9:00—9:15。模型的结果调整了高峰时段的需求,充分满足了容量约束的要求,同时一些潜在容量冲突时段也被做了平滑的调整,少部分航班被偏移到下午、傍晚和深夜相对空闲的时段。相比于时刻表最初的公平性情况,在整体公平性提高的同时,潜在冲突时段冲破容量约束的可能性也在战略层面上被进一步减小。
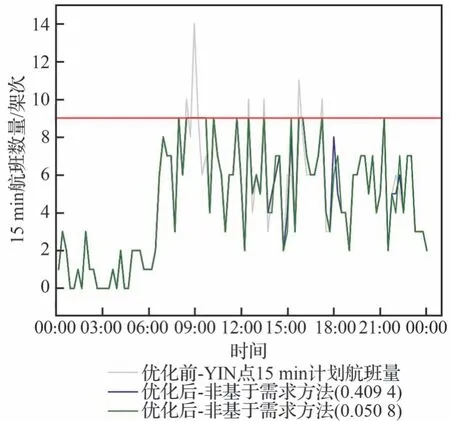
图10 非基于需求方法(0.409 4)和非基于需求方法(0.050 8)通过离场点YIN 的15 min 航班量Fig.10 Number of flights per 15 min through YIN obtained with the non-demand-based fairness method( 0.409 4) and the non-demand-based fairness method( 0.050 8)
4 总结与展望
本文在综合考虑机场群运行特征、空域结构、关键空域和航路点容量限制、航班时刻最大调整量、航班衔接需求以及离场点航班时刻分配的公平性的基础上,建立了基于共用离场航路点高峰需求的机场群航班时刻表优化的公平性模型。结合粤港澳大湾区机场群航班时刻数据,通过Gurobi求解器计算和分析,得出以下结论:
1) 基于高峰需求的机场公平性与非基于需求的机场公平性方法相比,前者的时刻表总偏移和基尼机场公平性达到了更好的权衡。
2) 基于高峰需求的机场公平性方法更加关注高峰时段的航班,其设定的高峰请求比例原则对高峰航班请求敏感,会进一步权衡高峰请求数量和航班偏移的关系:针对高峰时段需求,模型会通过增减高峰航班数量的方式调整对相应的航班偏移量。而非基于需求的机场公平性方法则凭借航班数量优势来“分摊”机场所获的航班总偏移,但这间接地惩罚了未处于高峰时段内的航班,不能体现航班层面的公平性。
3) 模型采用非基于需求的机场公平性方法,当考虑对各利益相关方绝对公平时,总偏移存在“突变”的极大值。针对时刻表总偏移进行单目标优化时,非基于需求的基尼机场公平性与总偏移的权衡效果较差,表现为:最小时刻表总偏移增加了15 min,但是对应的基尼机场公平性可以从0.409 4 减少到0.050 8,在YIN 航路点的机场群整体公平性大大改善。因为在非基于需求的机场公平性方法中,模型可能会通过牺牲机场群中部分机场的公平性的方式来换取整体公平性的提高,而基于高峰需求的机场公平性方法则会兼顾机场群中各机场在关键航路点的时刻需求。
4) 航班时刻调整结果表明:与YIN 航路点计划航班架次相比,被2 种机场公平性方法优化调整后的每15 min 的离场航班架次分布都更加均衡且满足航路点容量限制,航班时刻优化达到了“削峰填谷”的效果。值得注意的是,与非基于需求方法(0.409 4)相比,基于高峰需求方法(0.037 7)产生的航班时刻分配结果在13:45—14:30,17:45—18:30,21:45—22:30 等3 个非高峰时段均做了航班架次的调整,使得航班时刻的需求分布均向后移动,航班分布更加均匀平滑。
本文研究表明:基于高峰需求的机场公平性方法有潜力去更好地权衡机场群系统中航路点的效率和公平性,不仅仅局限在粤港澳大湾区机场群,也可以是中国和世界其他地区的机场群中。未来的研究有很多可能的拓展方向。首先,本文实例中的研究对象是一个五机场共用的离场航路点,未来可以进一步研究进场点和进离场混合的航路点;其次,实际上机场群内并非每个航路点都会有来自(去往)各机场的航班经过。对于机场群共有N个机场,但只有其中2~(N-1)个机场经过的航路点,如何考虑该点的航班时刻资源的机场公平性将是以后的研究方向之一;另外还可以进一步研究允许拒绝某些航班请求对各个航路点之间机场公平性的相互影响。解决这种具体细化的公平性问题将进一步增加模型的系统层面的考量;最后,本文虽然对机场和航路点都分别做出15、60 min 的航班容量约束,但为了能够更好地均衡匹配航班需求、平滑航班量分布,可以将容量约束的时间间隔逐渐缩小至5 min,并且采用滚动容量的约束形式,使得航班时刻分配更加精细化。
(责任编辑:宋金超)

