变弯度机翼参数化气动弹性建模与颤振特性分析
喻世杰,周兴华,黄锐
南京航空航天大学 机械结构力学及控制国家重点实验室,南京 210016
近年来,对航空航天飞行器执行复杂任务、适应不同飞行环境的能力要求越来越高,而变体飞行器因具有可根据任务类型和飞行环境的要求自主改变结构外形和气动布局的优点,受到了广泛关注。
变弯度机翼技术是一类典型的变体形式,可自适应改变翼型弯度改善飞行器气动性能。随着智能材料与结构技术的发展,变弯度机翼可望成为极具发展前景的变体技术。当前,国内外对变弯度机翼技术进行了一系列研究。例如,美国国家航空航天局(National Aeronautics Space and Administration,NASA)和美国空军研究实验室(Air Force Research Laboratory,AFRL)联合开展任务自适应机翼(Mission Adaptive Wing,MAW)[1-6]项目,改装了F-111 飞机的机翼后缘;在20 世纪末又启动了智能机翼(Smart Wing)[7-8]项目,利用基板弯曲控制后缘偏转;之后研究重心转移到柔性材料与机械驱动的组合,开展了自适应柔性后缘(Adaptive Compliant Trailing Edge,ACTE)[9]项目,在湾流III 飞机上应用并成功试飞。欧盟FP7(7th Framework Programme)计划包含了基于可变后缘的增升装置的研究[10],瑞士联邦材料科学与技术研究所的Campanile 通过改变辐条与蒙皮的间隔实现了机翼的变弯度[11],德国宇航院(Deutsches Zentrum für Luftund Raumfahrt,DLR)的Sinapius 等[12]提出手指方案对机翼变弯度实现了单自由度驱动。中国关于变弯度机翼的研究仍处于发展之中[13],西北工业大学刘世丽等[14]研究了机翼分布式柔性结构方案,南京航空航天大学李飞[15]设计了基于形状记忆合金的差动驱动自适应机翼结构,哈尔滨工业大学黄建[16]把新型零泊松比蜂窝结构应用在变弯度机翼中。
上述研究主要集中于变弯度机翼的驱动和结构设计等问题,少有关注变体过程的动力学问题,尤其是变体过程的气动力变化及参变气动弹性稳定性问题少有研究[17]。西北工业大学倪迎鸽[18]、南京航空航天大学赵永辉等[19-20]均采用偶极子网格法(Doublet-Lattice Method,DLM)构建了折叠机翼的参数化气动弹性模型[21],分析了折叠角对变体机翼颤振特性的影响规律;北京航空航天大学杨宁等[22]利用DLM 对考虑结构非线性折叠翼进行了颤振分析。但DLM 是一种基于平面假设的方法,该方法无法考虑机翼弯度影响,更无法研究具体变弯度过程的气动特性变化规律,因此DLM 无法用于变弯度机翼的气动弹性研究。目前较为通用的方法是基于CFD 的变弯度机翼非定常气动力计算分析。例如,西北工业大学刘艳[23]研究了采用连续变弯度后缘舵面系统的弹性翼飞机气动弹性计算和结构优化问题,北京航空航天大学吴优等[24]基于Open-FOAM 模拟了连续变弯度翼型的动态气动特性。虽然CFD 方法具有高保真度,但对于研究变体过程中引发的参变气动弹性稳定性方面,存在颤振边界丢失等问题,且计算效率低,需耗费大量的时间[25-29]。在变弯度机翼的参数化建模,国内外研究者采用自由型面变形(Free Form Deformation,FFD)技术实现了变弯度参数化建模[30-32],但需耦合基于RANS(Reynolds Averaged Navier-Stokes)方程的CFD 求解器,依旧存在CFD 固有缺陷,也未明确在参变条件下机翼颤振边界的变化趋势及其中的颤振机理。因此,对于变弯度机翼的参变气动弹性问题,迫切需要一种高效、准确的非定常气动力计算方法,并耦合参变结构动力学模型,进而高效、准确预测变体过程的气动弹性特性[33]。非定常涡格法(Unsteady Vortex Lattice Method,UVLM)是一种基于时间步长的非定常时域气动力计算,可动态捕捉附着涡和尾涡对分布式气动载荷的影响,能分析机翼在弯度变化下的参变气动弹性特征,计算速度较传统方法有很大提升,是一种兼顾计算效率和精度的折衷方案。对于柔性机翼的低速非定常气动力问题,可采用UVLM 进行气动力建模和响应求解[34]。
综上所述,为解决如何高效计算、分析全参数域下,变弯度机翼的气动弹性稳定性问题,克服DLM 方法无法考虑变弯度效应,而直接CFD计算方法成本过高等困难,本文提出一种基于流形切空间插值和非定常涡格相结合的连续变后缘机翼参数化气动弹性建模方法,避免了传统方法中针对不同参数需重复建模的问题,提高了计算效率,且能精确高效地捕捉机翼在全参数空间内的气动特性的变化,并分析、预测了机翼在翼型弯度变化下的气动特征变化机理及趋势。
1 变弯度机翼参数化气动弹性建模
变弯度机翼的几何外形及内部结构如图1 所示,机翼的后缘变弯度角θ在0°~30(°最大变形状态)变化。其中可变后缘部分占机翼弦长的56%,两端的柔性引导面可向下延展,以保持变形过程中的翼面连续性。变形过程中只有可变后缘部分的上下蒙皮发生弯曲变形,维持了变弯度时的结构和气动的连续性,有效地避免了机翼主要承力结构发生弹性变形,可在变形过程中保持良好的稳定性。
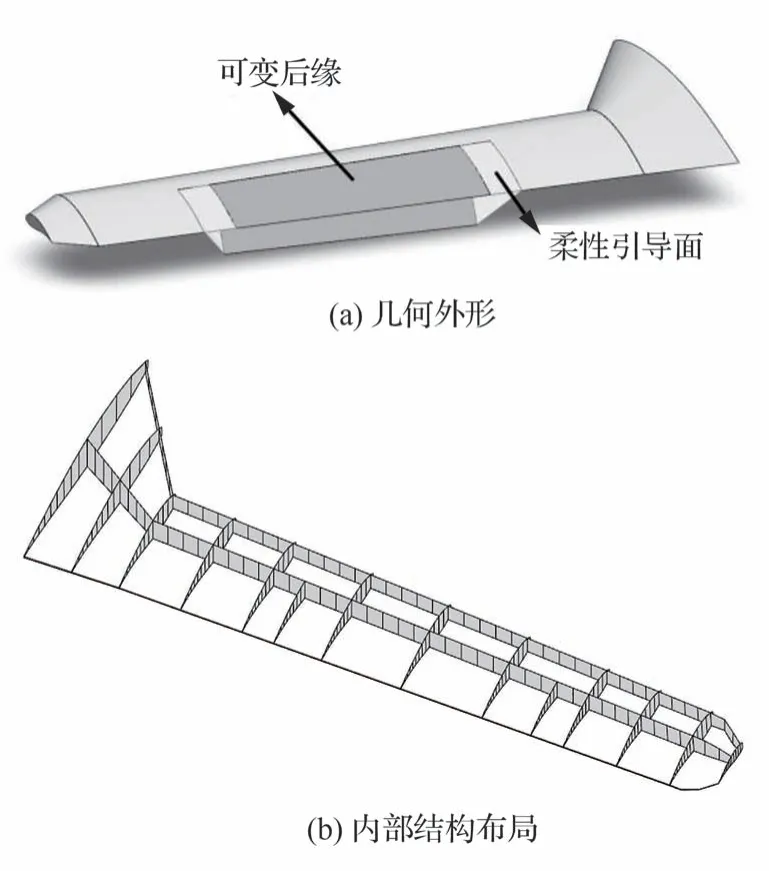
图1 机翼模型结构设计Fig.1 Structural design of wing model
1.1 参数化结构动力学建模
设定初始未变形状态的机翼模型后缘变弯度角θ=0°,建立初始结构模型,对其离散化获得有限元模型,结果如图2 所示。

图2 机翼有限元模型( θ=0°)Fig.2 Finite element model of the wing( θ=0°)
有限元模型主要采用壳、杆和梁单元构建,来传递翼面压力,承受机翼气动力和传递气动力矩。网格模型共有1 632 个节点,考虑翼根固支边界条件的影响,节点自由度N=9 588。对模型不同部位赋予不同的材料参数如表1 所示。
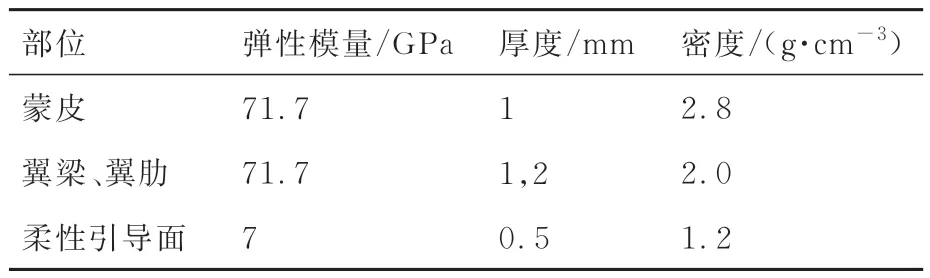
表1 模型参数Table 1 Parameters of the model
变弯度机翼运动方程依赖于机翼的参数变化,即受后缘变弯度角θ的影响。后缘弯度发生变化时,建立运动方程所需的质量与刚度矩阵都会发生变化,因此需要对机翼结构参数化建模。在传统的建模方法中,在每个不同变弯度角θ下,都要重新构建结构模型,计算量巨大,增加了时间。因此本文利用流形切空间插值(Manifold Tangent Space Interpolation,MTSI)方法,通过有限个不同参数的初始模型拟合出全部参数变化条件下的结构动力学模型[35-37]。
采用节点坐标变换的方式获取变弯度角分别为θ1=0°、θ2=15°和θ3=30°的可变后缘节点坐标,进而得到3 个初始位置的整体有限元模型,结果如图3 所示。
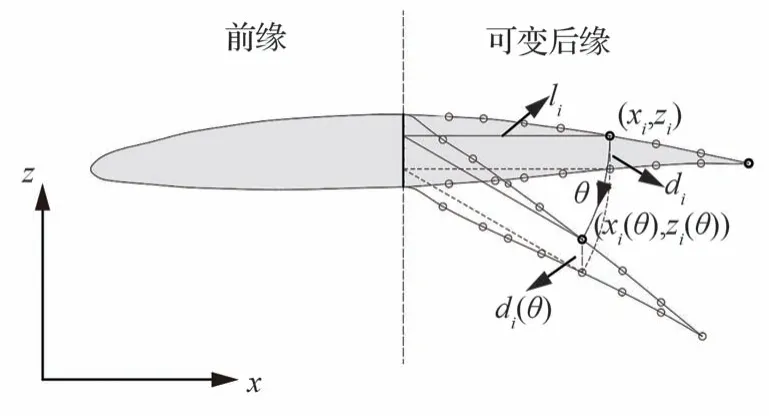
图3 节点坐标变换Fig.3 Coordinate transformation of node
通过有限元软件分析求解3 个初始位置有限元模型的质量矩阵M(θ1)、M(θ2)、M(θ3)和刚度矩阵K(θ1)、K(θ2)、K(θ3),从而获得包含前6 阶模态的结构振型Φr(θ1)、Φr(θ2)、Φr(θ3),再对矩阵降阶。
质量矩阵的参数化建模:上文中得到的Mr(θ)均为对称正定(Symmetric Positive Definite,SPD)矩阵,张成的空间为SPD 流形,记作MSPD。取Mr(θ3)为插值原点M0,MSPD的对数映射为
式中:logm 为矩阵对数;Γi为Mr(θi)由MSPD映射到其切空间,记作TM0MSPD的投影点所对应的矩阵。
切空间TM0MSPD是“平直”向量空间,在切空间上可以利用Lagrangian 插值法对Γi插值,得到任意变弯度角θk的模型在TM0MSPD中的插值矩阵Γk为
MSPD的指数映射为
式中:expm 为矩阵指数;Mr(θk)为Γk由TM0MSPD映射到MSPD的投影点所对应的矩阵,即目标参数降阶质量矩阵。同理可得到目标参数降阶刚度矩阵Kr(θk)。MTSI 插值方法的示意图见图4。
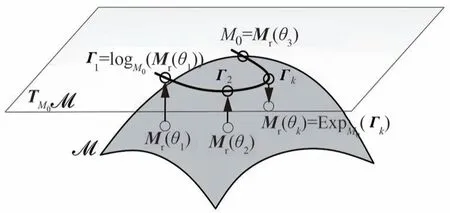
图4 流形切空间插值示意图Fig.4 Schematic diagram of manifold tangent space interpolation
振型矩阵的参数化建模:由于振型矩阵不处于SPD 流形,引入Φr(θi)T的Moore-Penrose 广义逆Ψ(θi)作为约束矩阵,满足
式中:I6为6 阶单位矩阵。
Grassmann 流形是y维欧几里得空间中所有通过原点的x维平面集合,记作G(x,y),Φr(θ)的第j列(即第j阶(j=1,2,…,6)模态对应的振型)张成的特征子空间可以视作流形G(1,N)上一点。取Φr(θ3)的第j列作为插值原点Φ0j,G(1,N)的对数映射为
式中:Φij表示振型矩阵Φr(θi)对应的第j列。
同理利用式(3)得到变弯度角θk下的振型矩阵单列在切空间中插值结果Γkj。G(1,N)指数映射为
采用Gram-Schmidt 正交化方法使得Φkj满足正交约束条件
式中:Ψkn表示约束矩阵Ψ(θk)对应的第n列。
利用同样的方法可以得到满足正交约束条件的Ψkj,且有=1。最后,通过缩放使Φkj和Ψkj的2 范数大小与插值原点保持一致,得到参数化振型矩阵Φr(θk)=[Φk1Φk2…Φk6]。后文所用的振型Φ均为截断振型,省去下标r。
1.2 非定常气动力建模
如图5 所示,基于非定常涡格法,划分机翼升力面的气动网格并标注非定常参数。
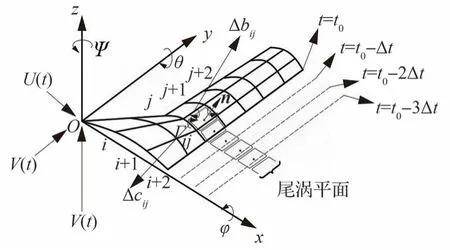
图5 机翼升力面非定常参数Fig.5 Unsteady parameters of wing lift surface
位于(i,j) 处的涡环Q(i,j,Γij) 在任意点P(x,y,z)引起的诱导速度为
式中:fiv为诱导速度计算函数。
利用2 个相邻时间步的后缘涡格后节点的位置创建尾涡涡格,重复此过程以模拟尾涡脱落过程如图6 所示。
则有
式中:Γwt为当前时间步脱落的尾涡强度;Γtet-Δt为前一时间步后缘附着涡强度。
在第K个控制点(即第i,j个涡格)上指定无穿透边界条件为
式中:n为涡格法向量;m为附着涡总数;U∞为来流速度;vη为升力面在该控制点的变形速度;(uw,vw,ww) 为尾涡诱导速度(通过式(11)和式(12)计算并求和得出)。则第K个附着涡的涡强为
由伯努利方程可得分布压力差的计算公式:
式中:ρ为空气密度;Δci,j和Δbi,j分别是对于第i,j个涡格的i和j方向的长度(见图5);τii,j和τji,j分别是对于第i,j个涡格的i和j方向的切向向量。
最终得到分布气动载荷:
式中:ΔSij为第i,j个涡格的面积。
与传统气动网格平面相比,UVLM 方法不再局限于平面无弯度翼型,为将参数化结构动力学建模和UVLM 计算方法相匹配,需建立一个可随参数变化的气动网格模型,本文选取参数变化后结构的中弧面。利用排序与分类算法提取出有限元结构的上下表面节点顺序序列,并根据其顺序重新构造上下曲面网格,得到当前变弯度角下的气动网格模型。
获得的各变弯度角下的气动网格模型如图7所示。
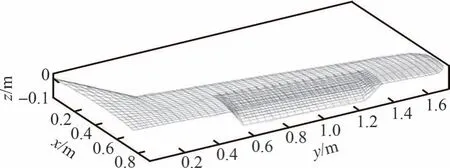
图7 不同变弯度角下的气动模型Fig.7 Aerodynamic model with different camber angles
1.3 流-固耦合插值建模
对机翼结构进行有限元分析可获得结构网格节点处的模态振型,通过非定常气动力建模方法可获得涡格控制点的分布气动载荷。为进一步得到气动网格节点处的模态振型及其等效空气动力,利用无限板样条插值(Infinite Plate Spline,IPS)方法来实现对于模态振型和气动力的插值[38]。即对于结构模态振型向量us和气动模态振型向量ua,由载荷向量的平衡关系可得样条插值矩阵G,满足的条件为
针对气动模型模态振型求解:通过式(19)构造出机翼结构的中弧面网格,对于任意节点(xk,yk)都能在机翼结构网格的上下表面分别找到与之唯一对应节点(xi,yi)与(xi',yi'),有xk=xi=xi',yk=yi=yi'。因此可得中弧面的模态振型:
式中:Φs为有限元结构振型。
因为气动面与中弧面构造方法一致,所以G为单位矩阵,通过式(22)计算气动网格的模态振型为
针对速度和气动载荷的求解,由式(20)得到气动网格节点向涡格控制点插值的样条插值矩阵Ga。设气动网格节点的速度矩阵为va,则有
式中:vc为控制点的速度矩阵;Fa为气动网格节点的气动力矩阵。
1.4 参数化气动弹性建模
前面已经获得了任意变弯度角θ下机翼有限元结构模型的降阶质量矩阵、降阶刚度矩阵及截断振型。忽略阻尼的影响,构建参变气动弹性方程的一般形式为
式中:Fg为广义气动力,其表达式为
在参变条件下,式(11)~(式18)给出了非定常气动力建模方法、式(22)~式(24)给出了流-固耦合插值建模方法、式(25)~式(27)给出了气动弹性建模法,综合上述方法计算不同变弯度角的机翼模型在不同来流速度下时域响应。通过每一时刻的模态位移响应可构造得随时间变化的气动网格及其涡格,通过每一时刻的模态速度响应可计算随时间变化的诱导速度,这两项的改变造成了气动力的变化。最后利用稳定状态时域响应的敛散性来确定机翼的颤振边界,分析不同变弯度角对于机翼颤振特性的影响及其规律,实现了在给定风速条件下对机翼模型的时域响应分析,整体流程图如图8 所示。
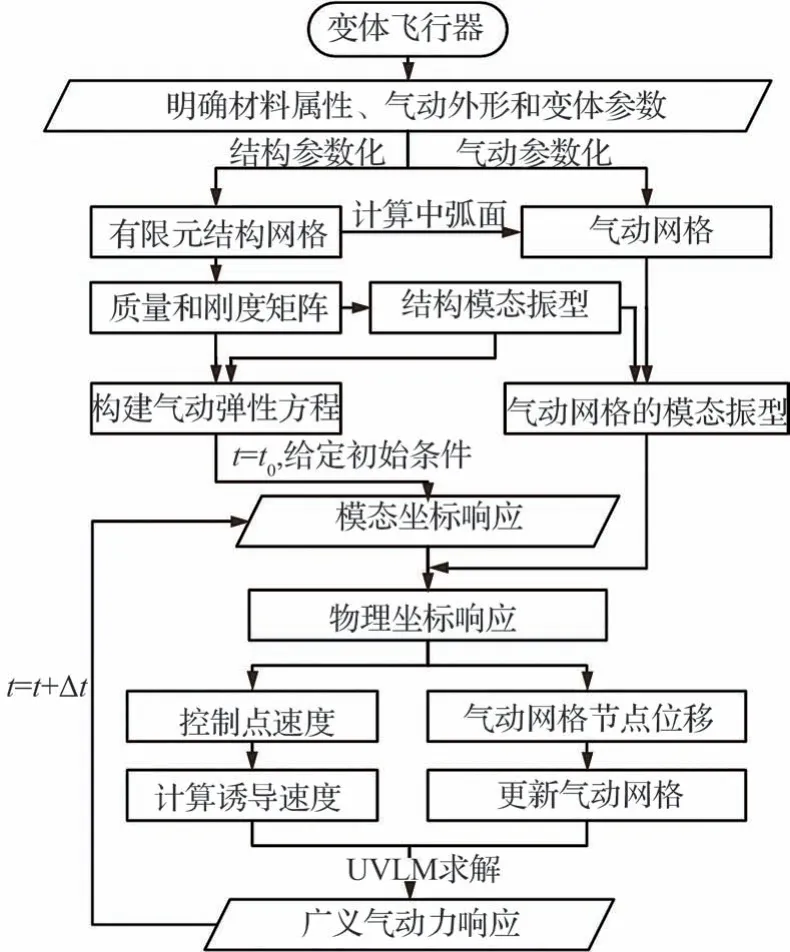
图8 气动弹性建模流程图Fig.8 Flow diagram of aeroelastic modeling
2 数值仿真与验证
2.1 变弯度机翼参变结构动力学特性与验证
为分析不同变弯度角下机翼的结构动力学特性,利用流形切空间插值方法,在0°~30°间隔2.5°选取共13 个后缘弯度位置的参数化矩阵,以此获得不同变弯度角下模型的前6 阶固有频率及固有振型,并利用节点坐标变换方式直接计算得到相应的频率和振型作为对比。固有频率对比结果如图9 所示,变化曲线基本一致拟合效果较好,最大误差出现在θ=5°的第2 阶模态处为3.6%。
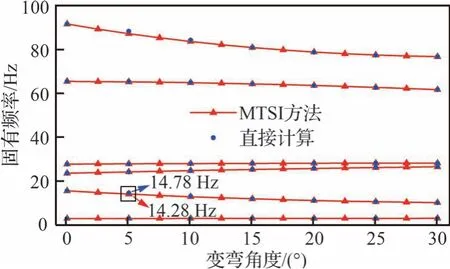
图9 固有频率对比Fig.9 Comparison of natural frequencies
θ=5°时的固有振型的对比结果如图10 所示(黑色为未变形状态,红色为MTSI 插值模态振型,蓝色为直接计算模态振型)。由图10 可知:由于机翼展弦比较大,前6 阶模态中包含面内运动(一阶面内弯曲),不过面内振动几乎不引起非定常气动力,对机翼的气动弹性特性影响不大。

图10 MTSI 方法计算的固有振型Fig.10 Natural mode shapes by MTSI method
模态置信准则(Modal Assurance Criterion,MAC)值是振型向量之间的点积,用于检验模态振型的相关性。不同变弯度角下参数化模态振型与直接计算模态振型的MAC 值如表2 所示,作为依据验证参数化模态振型与直接计算模态振型的误差。
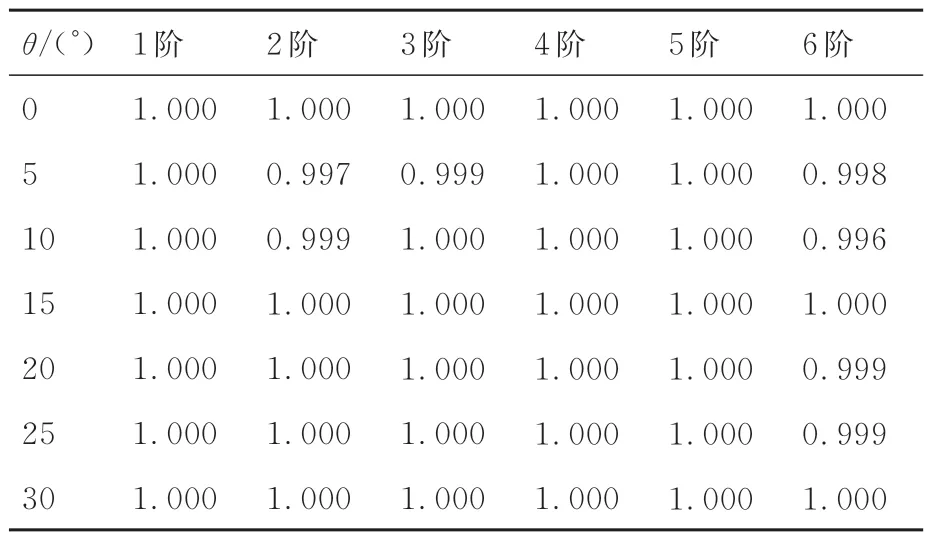
表2 固有振型MAC 值Table 2 MAC value of natural mode shapes
由图10 和表2 可得:参数化模态振型与直接计算模态振型吻合较好,在高阶模态(第6 阶)及θ=5°的第2 阶模态处存在一定误差,与图9 中的频率误差分布相近,但数值均不低于0.996,满足工程指标要求,验证了参数化结构动力学建模的准确性。
2.2 流-固耦合插值验证
为了验证IPS 插值方法的准确性,本文将θ=5°的IPS 插值气动模态振型与图10 中的MTSI 结构模态振型进行对比验证,结果如图11所示(红色为IPS 插值气动模态振型,蓝色为MTSI 结构模态振型)。由图11 可知,插值得到的气动网格模态振型与参数化结构模态振型基本一致,验证了插值方法的准确性。

图11 插值模态振型对比Fig.11 Comparison of interpolated mode shapes
2.3 非定常气动力验证与计算
为验证非定常气动力计算方法的准确性,采用Theodorsen 非定常气动力理论与本文非定常气动力方法比较,计算二元翼段俯仰角非定常气动力,简谐运动为
翼段具体参数见表3。利用本文方法建立相同的气动模型,增大展弦比以忽略机翼三维效应的影响,其余参数同表3。对比结果如图12所示。
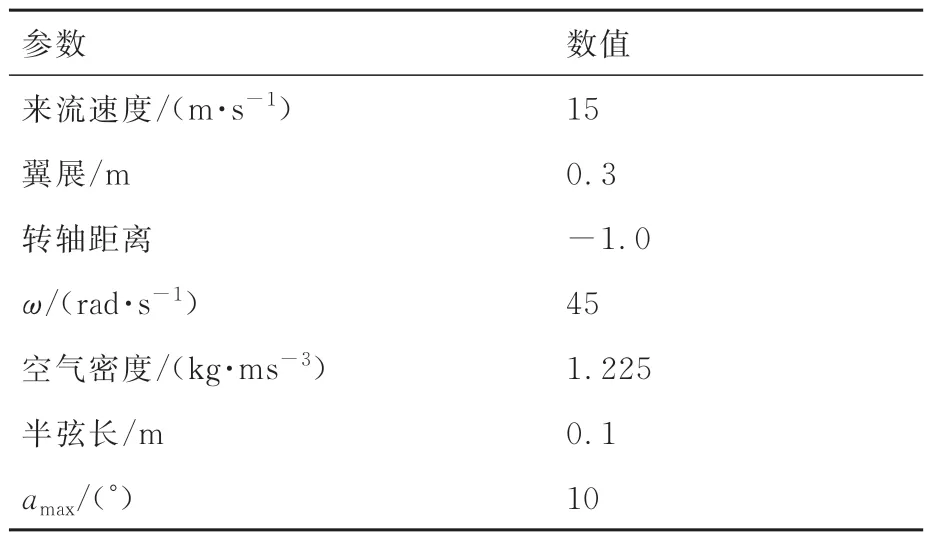
表3 翼段参数Table 3 Parameters of wing segments
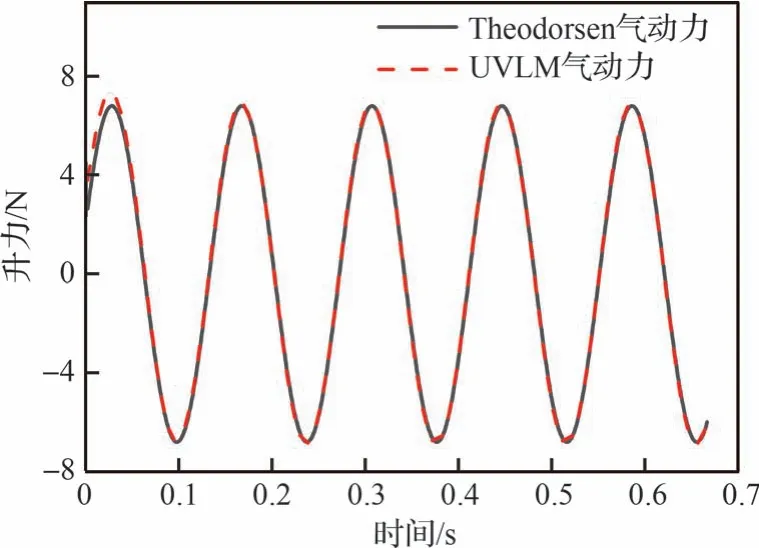
图12 Theodorsen 与UVLM 非定常气动力对比Fig.12 Comparison of unsteady aerodynamic forces calculated by Theodorsen theory and UVLM
由图12 可知,UVLM 算法计算得到的非定常气动力与Theodorsen 气动力吻合良好。为进一步研究UVLM 算法对气动力的计算效果,本文在给定条件下(不考虑弹性变形,给定风速10 m/s,初始迎角0°),计算各变弯度角下机翼的定常气动力系数的展向分布及随弯度角变化的总体气动力系数的变化情况,结果如图13 和图14 所示。
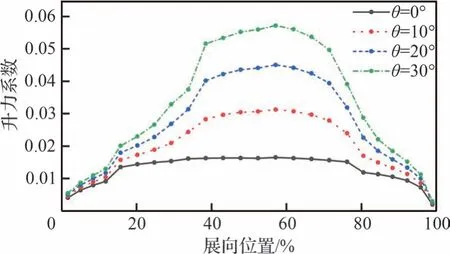
图13 升力系数展向分布Fig.13 Spanwise distribution of lift coefficient
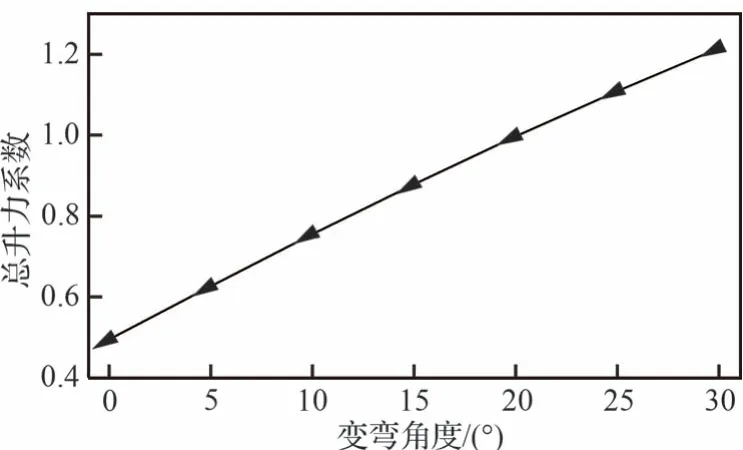
图14 总升力系数随弯度角的变化Fig.14 Variation of total lift coefficient with camber angle
2.4 颤振计算方法验证
为验证本文所用颤振计算方法的准确性,构建与机翼模型投影相似的平面机翼模型(忽略翼型的影响以满足验证算法的条件),分别利用本文方法与偶极子网格法进行颤振分析对比。
构建图15 所示的机翼模型。有限元单元仅使用壳单元,边界条件为根部固支。将结果提交至软件中利用偶极子网格法计算,根轨迹结果如图16(a)所示(沿箭头方向来流速度逐渐增大),颤振速度18.4 m/s,颤振频率3.15 Hz。

图15 平面机翼网格Fig.15 Mesh of wing in plane
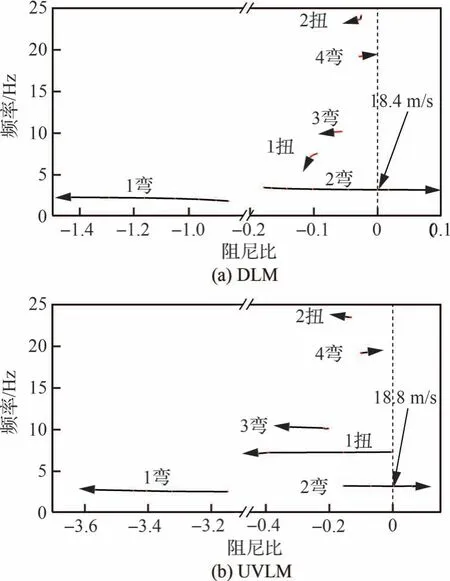
图16 DLM 与UVLM 根轨迹对比Fig.16 Comparison of root locus by DLM and UVLM
再利用本文方法获得该模型在颤振点附近的时域响应。为在频域中直观地分析颤振速度与颤振模态,通过动态模态分解(Dynamic Mode Decomposition,DMD)方法[39],辨识不同风速下系统的特征值并排序,得到机翼各阶模态的阻尼比和频率随来流速度变化情况,同样绘制出根轨迹,结果如图16(b)所示,颤振速度18.8 m/s,颤振频率3.15 Hz。结果表明,本文方法计算所得的机翼颤振特性与偶极子网格法计算所得的吻合良好。
2.5 参变颤振计算
对不同变弯度角下机翼模型的颤振边界计算与分析。对于给定变弯度角,判断时域模态响应在不同风速下的敛散性,找出此时模型的颤振区间上下边界如图17 所示(以θ=5°的时域响应为例),以此为基准可进一步确定该角度下模型的精确颤振速度。
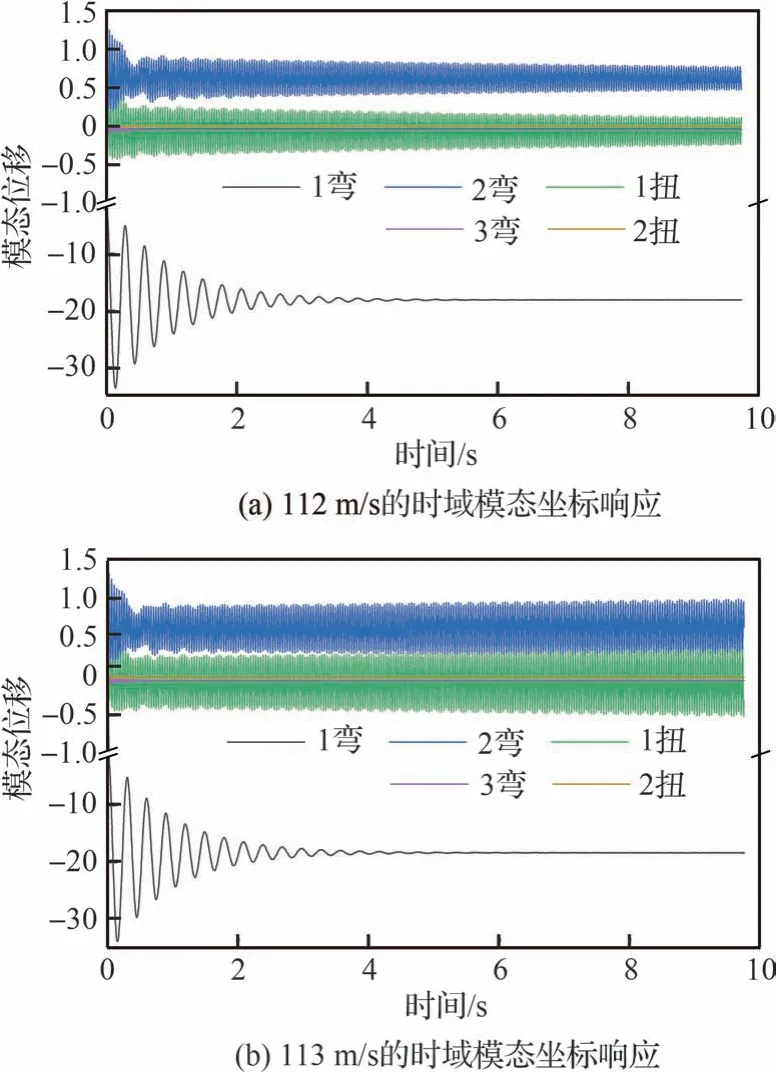
图17 θ=5°机翼颤振区间Fig.17 Flutter interval at θ=5°
通过上文所述的DMD 方法,对参变条件下的时域响应进行频域分析,求得风速变化条件下不同变弯度角的根轨迹,以此分析参变条件模型颤振前后的模态特征变化,结果如图18 所示。由图18 可知,机翼模型在各弯度角下的颤振均由1 阶扭转模态失稳引起。对于1 阶面内弯曲模态,由于其面内振动的特性,在颤振被激发时并不参与振动,根轨迹均位于左半平面且无序分布,因此图18 中并未画出。对于其他阶模态,随着风速的增加,阻尼比数值均在减小,且大部分模态频率向颤振频率靠近。
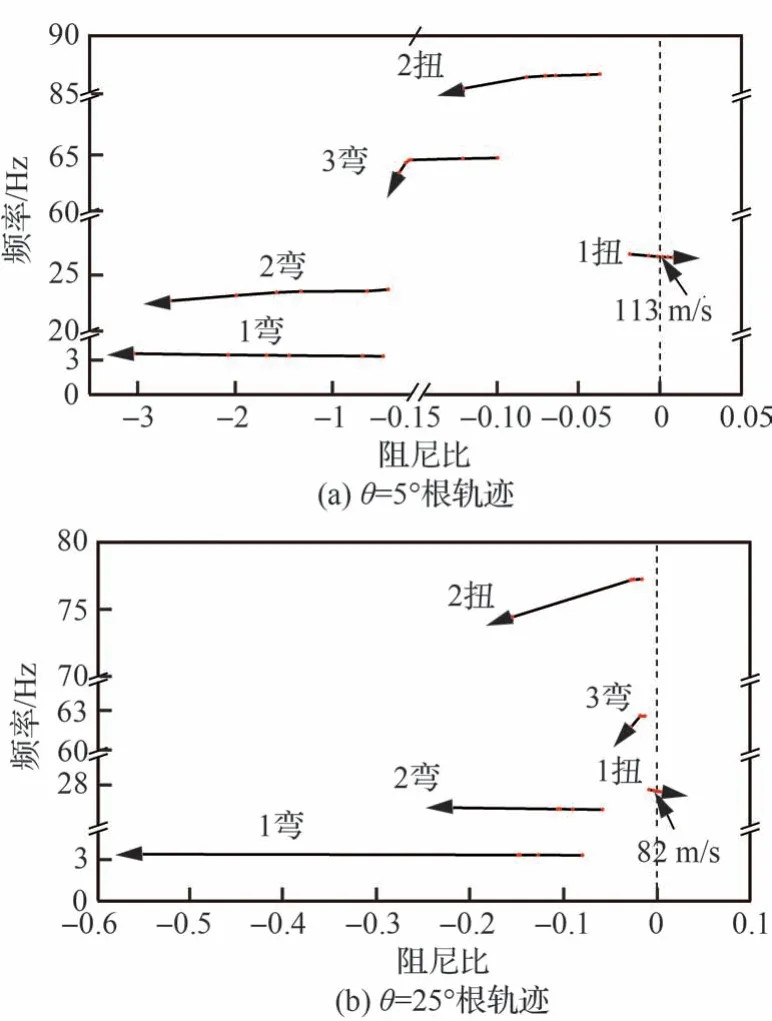
图18 参变根轨迹Fig.18 Root locus with parameter variation
为进一步分析各变弯度角下颤振发生时的模态成分,本文利用不同变弯度角下模型在各自临界颤振状态下的模态响应做频谱分析。取稳定状态的时域响应数据进行快速傅里叶变换处理,结果如图19 所示。
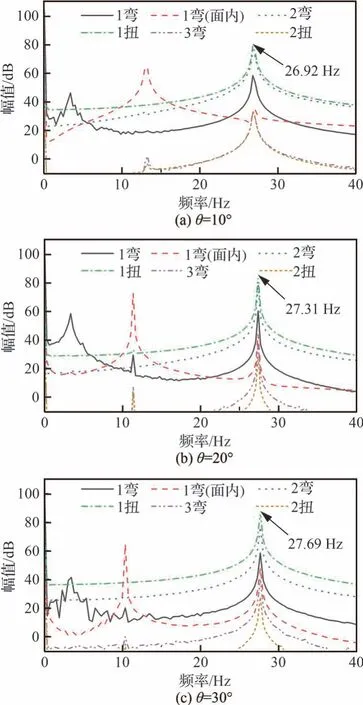
图19 不同变弯度角下各阶模态位移的频谱分析Fig.19 Spectral analysis of each modal displacement at different camber angles
图19 中均出现了2 个明显峰值,较小值与1 阶面内弯曲模态的固有频率接近,较大值为该变弯度角下的颤振频率。由图19 分析可知,在后缘偏转角度较小时,2 阶弯曲和1 阶扭转模态为主要颤振模态,除1 阶面内弯曲外各阶模态的主要频率均为颤振频率。随着后缘弯度角的增大,1 阶扭转模态成分占比逐渐增大,1、2 阶弯曲模态成分占比逐渐减小。随着可变后缘的偏转,机翼后缘段的定常气动升力逐渐增大,机翼的颤振形式由弯曲向扭转过度,所以1 阶扭转模态对颤振的影响逐渐增大,1、2 阶弯曲的影响逐渐减小。机翼模型的颤振速度和颤振频率随弯度的变化如图20 和图21 所示。
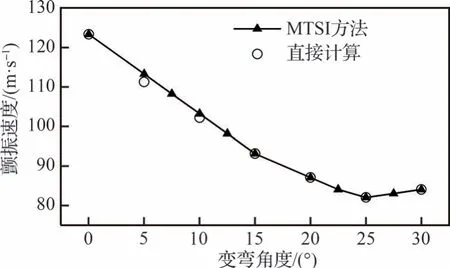
图20 颤振速度随弯度角的变化Fig.20 Variation of flutter speed with camber angle
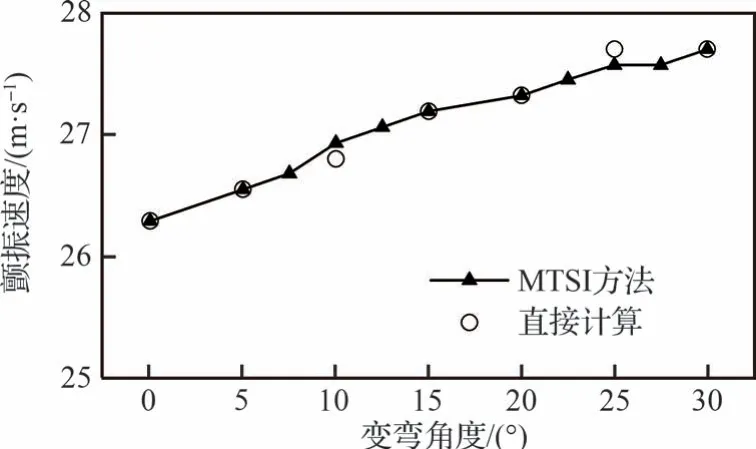
图21 颤振频率随弯度角的变化Fig.21 Variation of flutter frequency with camber angle
仿真验证表明颤振速度拟合效果较好,颤振频率拟合存在一定差异。在低偏转角时,随着后缘弯度的增大,机翼颤振速度逐渐减小,颤振频率逐渐增大,机翼可变后缘部分的翼型弯度逐渐增大,机翼的定常气动力变大,使其颤振边界降低。同时由于后缘偏转,增大了气动力对机翼扭转的影响,使机翼1 阶扭转模态对颤振的贡献度增大,进而降低了颤振速度,颤振频率也向1 阶扭转模态频率靠近,提高了颤振频率。在高偏转角之后,1 阶扭转模态完全主导颤振,颤振速度也不再因弯度角的增大而产生较大变化,解释了此时颤振频率变化趋于平缓的原因。
3 结 论
针对变弯度机翼的参数化建模以及颤振计算的问题,提出了基于流形切空间插值和非定常涡格法相结合的变弯度机翼参数化气动弹性建模方法,高效准确地分析了变弯度机翼的参变结构特性和气动弹性力学特性,并对机翼模型的气动性能、非定常气动力计算、插值方法、颤振计算均进行了数值仿真与验证,主要结论如下:
1)实现了连续变弯度机翼在全参数空间内的精确化建模,包含结构参数化建模、非定常气动力建模、流-固耦合插值和气动弹性模型建模。可以减少不同参数模型重复构建的次数,降低结构模态计算的时间消耗。同时准确地模拟机翼在不同外形参数下的结构动力学特性,可在时域分析中综合考虑机翼弯度、机翼弹性变形带来的影响,对参变气动性能进行有效分析。
2)利用该方法对变弯度机理分析,分别从时域和频域两个角度深入研究了不同弯度角下机翼的参变特性。探讨了机翼随弯度角变化引起的参变颤振特性,计算并分析了不同变弯度角模型的颤振边界和颤振模态成分,研究了机翼随变弯度角变化引起的模态特征的变化趋势及其原因:随着变弯度角的增大,机翼的颤振速度增大而颤振频率减小,但在一定角度后,由于1 阶扭转模态的主导性,机翼颤振受其他各阶模态的影响较小,导致颤振速度的变化出现阈值,速度和频率的改变趋于平稳。
3)本文的参数化建模方法可扩展应用到其他结构可变机翼构型(例如可折叠机翼、变后掠机翼等),在参变条件下对飞行器进行气动弹性建模与分析,具有贴合工程实际的普适性意义。但本文提出的参数化建模方法仍有一些值得深入研究的问题。例如,仍受到气动力模型和计算效率的限制,仍无法考虑翼型厚度的影响等。此外,需要深入探索该方法对于时变问题的应用,进而为变体飞行器的时变气动弹性力学研究提供高效、准确的建模方法。

