基于多分类SVM算法的癫痫发作自动检测方法

王元发,庞 宇,周前能,黄志伟

(1.重庆邮电大学 光电工程学院,重庆 400065;2.西南医科大学 医学信息与工程学院,四川 泸州 646000)

0 引 言

癫痫是由脑部神经异常放电引起的慢性疾病,长期频繁的癫痫发作会对患者的身心、智力产生严重影响。如果癫痫发作未及时发现与治疗,会因高热、循环衰竭、神经元损伤导致不可逆的脑损伤,给患者及其家人造成极大的痛苦和伤害[1-2],且癫痫的突然性发作可能导致生命危险[3]。及时、准确地检测癫痫疾病并采取对应的治疗或控制措施,不但可以减轻患者的痛苦及其家庭的负担,而且可以提高患者的健康水平。目前脑电图(electroencephalogram,EEG)检测由于其无创、方便的特点在癫痫疾病检测中扮演着重要的角色。传统的检测方法是由医疗工作者对患者EEG信号长时间监测,并根据临床经验视觉诊断[4-5]。该方法耗时,效率低下,而且不方便。近年来,专家学者提出了一种基于计算机软件技术以及智能分类算法的癫痫EEG信号自动检测方法。本文研究一种高性能的多分类器,用于区分正常、癫痫发作和发作间期EEG信号,在临床上具有重要意义。

通过机器学习算法对癫痫EEG信号训练与自动识别是一种常用的方法[6-7]。近年来,许多机器学习算法,包括人工神经网络(artificial neural network,ANN)[8-9]、K邻近(k-nearest neighbor algorithm,KNN)[10]、朴素贝叶斯(Naive bayes classifier,NB)[10]、线性判别分析(linear discriminant analysis,LDA)[11]、支持矢量机(support vector machine,SVM)[12-14]、极限学习机(extreme learning machine,ELM)[6]以及最小二乘回归[15]等用在EEG信号自动检测中并取得较好的检测效果,其中SVM处理非线性EEG信号由于良好的性能引起极大的关注。文献[16-17]通过仿真对比了KNN、NB、LDA、SVM几种分类算法,得出SVM可以取得较好分类性能的结论。SVM具有较好的分类性能和泛化能力被广泛应用到癫痫EEG信号的自动分类识别中[18-19]。本文采用SVM算法自动检测癫痫EEG信号。由于癫痫EEG信号数据样本较大,传统SVM的训练算法将耗费大量时间。文献[20]提出SVM的序列最小优化(sequential minimal optimization,SMO)算法,可以用于大样本快速训练。文献[21-22]对SMO算法进行改进,提出了改进的SMO算法(modified SMO,MSMO),减少了计算上的浪费,进一步加快了SVM的训练速度。因此,本文采用MSMO算法对EEG信号进行训练。

从分类的角度讲,SVM本质是一个二分类算法,而对于同时区分正常、癫痫发作和发作间期EEG信号等实际问题,需要用到多分类SVM。通过多个二分类SVM构建的多分类方法有一对一、一对多、有向无环图、纠错输出编码和二叉树(binary tree,BT)[23-24]等方法。对区分正常、癫痫发作和发作间期EEG信号的三分类问题,一对一、一对多、有向无环图、纠错输出编码需要构建3个SVM分类器,二叉树多分类SVM只需要2个分类器。

特征提取作为EEG分类识别中的重要组成部分,直接影响EEG信号的分类性能。针对非线性非平稳的EEG信号,离散小波变换(discrete wavelet transform,DWT)在时频域具有较好的分辨能力,已被证实处理EEG信号是一种有效的工具[7,15,19]。研究表明,DWT更适用于EEG信号棘波的检测。同时,形状类似于棘波的Daubechies 4(db4)母小波能够有效地处理癫痫EEG信号。常用的DWT滤波器设计基于卷积运算,而该算法计算复杂度较高并且运算过程中需要较大的内存[25]。为了克服这些缺点,本文采用提升小波变换(lifting discrete wavelet transform,LDWT)算法对癫痫EEG信号进行分解。同时,采用LDWT的多分辨率分解将EEG信号分解为不同频段的子带信号,然后有选择性地提取不同频带EEG信号的特征量。

基于LDWT、MSMO及BT的优点,本文提出了一种高性能的癫痫及癫痫发作EEG信号自动检测方法,实现正常、癫痫发作和发作间期EEG信号分类识别。首先,将原始EEG信号经多级LDWT,得到不同频段范围的子带信号,求得小波变换后数据的近似熵(ApEn)、Teager能量、局部波动率、自回归系数(ACF)、Hurst指数特征值;其次,采用随机效应模型的Fisher得分法,筛选具有较好分类性能的特征值构成高维特征向量,将高维特征通过MSMO算法对3类EEG信号进行训练;最后,采用二叉树多分类SVM实现EEG信号分类识别。

1 EEG分类识别算法与原理

1.1 癫痫EEG信号处理及特征提取

1.1.1 基于LDWT的EEG信号处理

在EEG信号处理中,采用LDWT可以减小存储、提高计算速度。小波提升策略的基本结构如图1所示。

图1 提升小波结构Fig.1 Structure of the LDWT

图1中：Xo[n]和Xe[n]分别代表奇、偶序列;d[n]为预测产生的高频小波系数;s[n]为更新产生的低频小波系数;H[n]和L[n]为d[n]和s[n]分别归一化后的值。本文采用基于db4的4级LDWT将癫痫EEG信号分解为不同时频特性的子带信号。

1.1.2 自相关系数特征提取

自相关系数描述一个时间序列中先前数据值与之后数据值的相关程度,即度量这个时间序列过去对现在的影响[26]。根据EEG信号的特点,正常人的EEG信号非线性度和混沌性比癫痫患者强,通过自相关系数可以很好描述这种差别。第j级小波系数的L个连续时间序列的自相关系数为

(1)

1.1.3Hurst指数特征提取

基于重标极差(R/S)分析的Hurst指数是一种时间序列分形统计法,通过改变时间尺度的大小研究时间序列统计规律变化[27]。

对于一个时间序列xi(i=1,2,…,N),定义前k个数据点的平均误差为

(2)

R(n)=max(0,W1,W2,…,Wn)-

min(0,W1,W2,…,Wn)

(3)

(3)式中,n=1,2,…,N。定义R(n)/S(n)为

(4)

根据EEG信号特性,同时为了减小特征计算复杂度,本文将R(n)/S(n)的对数值作为特征值之一,记为logRS(n)。

1.1.4ApEn特征提取

研究表明,正常人的EEG信号时间序列比癫痫发作时更复杂,通过计算两者的ApEn值可区分正常人与癫痫患者[14,18]。

1.1.5 局部波动率特征提取

1.1.6Teager能量特征提取

癫痫发作时EEG信号常表现出高频率或者高幅值,通过Teager能量能够较好识别癫痫是否发病。离散Teager能量定义为[9]

ψ(x(n))=x2(n)-x(n-1)x(n+1)

(5)

(5)式中：ψ为Teager能量算子;x为原始EEG信号。

1.2 多分类识别算法

为了区分正常、癫痫发作和发作间期EEG信号,需要用到多分类SVM。图2为三分类的BT算法结构。

图2 三分类的BT结构Fig.2 BT structure for three-class

在训练阶段,第1个二分类SVM将类别1、2共同作为一类,类别3单独作为一类。第2个二分类SVM将类别1与2进行训练。当预测新的样本x时,通过第1个二分类SVM判别x所属类别。如果为类别3,即为最终结果;如果为类别1或2,需要利用第2个二分类SVM进行判别。从图2可以看出,二叉树多分类SVM在三分类问题中只需要2个分类器。

图3 非线性SVM分类器特征映射Fig.3 Feature mapping for non-linear SVM classifier

(6)

(6)式中：Ns为非零拉格朗日乘子个数,即支持矢量个数;K(·)为核函数,本文采用高斯核函数;yi∈{-1,1}为输入样本xi的标注类别;αi为训练产生的非零拉格朗日乘子。本文采用便捷、高效的MSMO训练算法对癫痫EEG信号进行训练,产生图2中BT算法的2个分类器模型。

2 本文方法

多分类EEG信号识别系统分为2个阶段：训练阶段和测试阶段。图4为癫痫EEG信号分类系统的训练和测试流程。采用4级小波变换将EEG分解为近似和细节小波系数,计算各小波系数的特征值构成高维特征向量,将标记类别的高维特征向量输入到MSMO中进行训练产生多分类器模型。训练结束后,未标记的EEG信号同样经过4级小波变换,并提取特征构成高维特征向量,通过多分类SVM自动识别为正常、癫痫发作或发作间期的EEG信号。

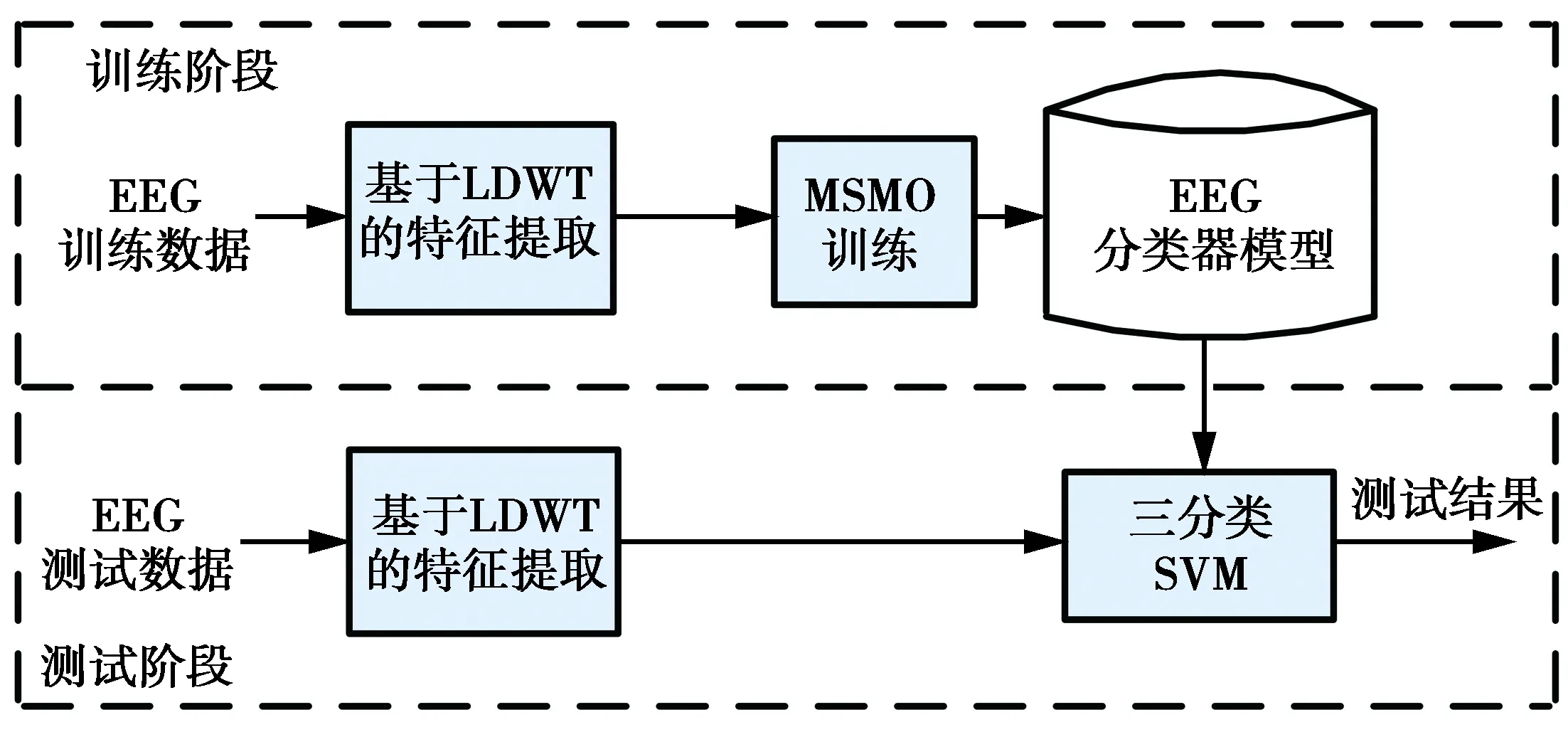
图4 三分类EEG信号分类流程图Fig.4 Workflow of the three-class EEG classification

2.1 实验数据

本文实验数据采用德国波恩大学公开发布的癫痫EEG信号数据库[14,28]。该EEG数据集共包含A、B、C、D、E 5类EEG信号子集,采样频率为173.6 Hz,每类信号子集包含100段EEG信号,每段信号包括4 096个采样数据点,每个数据段的时间长度都为23.6 s。数据子集A和B分别来自于5个正常人睁眼和闭眼状态;数据子集C和D来自于癫痫发作间期状态,其中C在癫痫病灶外区域采集,D在癫痫病灶内区域采集;数据子集E来自癫痫病人发作时状态。

2.2 特征提取优化及特征筛选

一个好的分类器,如果没有较好的特征提取方法,也难取得良好的分类性能,本文从不同视角提取EEG信号特征。

为了寻找ACF(n)中n为何值时分类性能较好,本文计算原始信号的自相关系数的前几项进行统计,正常人与患者EEG的ACF如图5所示,其中蓝色线段数据取自患者,绿色线段数据取自正常人。

图5 正常人与患者EEG的ACFFig.5 ACF values between healthy and epilepsy EEG

从图5可以看出,自相关系数的第5项分辨效果最强,也就是正常人与患者的ACF(5)值具有显著差异,因此选择这一项作为特征值之一,并作正常人与患者ACF(5)直方分布图如图6所示。图6中,蓝色取自患者,绿色取自正常人,可以看出两类数据具有显著的分辨效果。

图6 正常人与患者EEG的ACF(5)分布Fig.6 Histogram of ACF(5) between healthy and epilepsy EEG

图7是logRS(n)随log(n)变化图。图7中,蓝色曲线由患者数据计算得到,绿色曲线由正常人数据计算得到。在log(n)=1.9附近,两类数据的log(n)交叠部分很少,具有较高的区分度。图8所示为两类数据的logRS(60)直方分布图,可以看出两类数据的logRS(60)值分布差异显著,交叠区域小,具有较高的区分度,因此,将logRS(60)选作特征值之一。

图7 logRS(n)随log(n)变化Fig.7 logRS(n) versus log(n)

图8 正常人与患者EEG的logRS(60)分布Fig.8 Histogram of logRS(60) between healthy and epilepsy EEG

本文采用了随机效应模型中的Fisher得分法,筛选具有较高区分度的特征量[29]。设k是某一个待评估的特征值,现有两类数据A、B,每类数据有若干数据样本。先对A组数据的若干样本求特征值k,然后求k的平均值和方差,记为μA和σA。同理得到B组数据的μB,σB。于是A、B两组数据特征值k的Fisher得分记为IA,B,k,表示为

(7)

Fisher得分IA,B,k值越大,意味着特征值k的分辨效果越好。以近似熵为例,表1描述了各个信号近似熵的Fisher得分,得分越高表明这个特征值的区分度越高。根据计算结果,选取A1、A2、D1、D2的近似熵作为特征值。

表1 ApEn的Fisher得分Tab.1 Fisher scores of ApEn

根据上述方法,计算全部特征的Fisher得分,并选取得分值较高的几个特征。由于部分特征之间具有强相关性,而选择具有强相关性的特征对提高分类精确度没有显著贡献。因此,根据各个特征之间的相关性对特征组合进行微调和精简,筛选结果如表2所示。采用这些特征进行特征提取,构成高维特征向量作为三分类SVM的输入。

表2 特征筛选结果Tab.2 Results of the feature selection

3 实验结果与分析

3.1 三分类性能指标

对于区分正常、癫痫发作和发作间期3类问题,实验性能采用如下3个指标进行评价：敏感度(Sensitivity)、特异性(Specificity)、精度(Accuracy)。表3给出了三分类性能指标的详细定义[14,28]。表3中,SA、SD、SE分别表示A、D、E的epoch数;SAA表示从数据子集A中被分为A的epoch总个数;SAD表示从数据子集D中被分为A的epoch总个数;其他相应的参数可以通过类似方法解释。

表3 三分类性能定义Tab.3 Performance definition of three-class classification

3.2 结果与讨论

本文采用德国波恩大学癫痫EEG的A、D、E这3类数据对所设计的分类器进行性能测试。在EEG数据的预处理中,每1 024个数据点的时间窗构成一个epoch,为了弥补数据截断对EEG信号的连续性信息影响,在计算时将每个epoch数据进行50%交叠。为了验证将数据分割成epoch后对分类精度的影响,选择不同长度的epoch(1.47 s、2 s、2.94 s、4 s、5.1 s、5.9 s、23.6 s)对其产生的影响进行分析,随着epoch长度的增加,分类精度在不断提高。选择过长的epoch需要较长的时间检测出癫痫疾病,本文选择每个epoch的时间长度为5.9 s。每个数据段(Segment)被分为8个epoch,每一个数据子集共有800个epoch,A、D、E 3个数据子集共有2 400个。实验采用4-fold交叉验证对三分类系统进行性能测试。

为了分析4-fold交叉验证对特征筛选结果的影响,将交叉验证的4个训练集分别采用Fisher得分法进行特征筛选,结果基本一致。本文根据各个特征之间的相关性对特征组合进行微调和精简,实验采用表2的特征进行特征提取。

表4为样本长度为5.9 s时,三分类系统的精度、特异性和敏感度结果。表5为样本长度为23.6 s的分类性能。从表5的结果看出,系统的各项指标均为100%。

表4 样本长度为5.9 s时系统实验结果Tab.4 Rsults of the system when epoch length is 5.9 s %

表5 样本长度23.6 s时系统实验结果Tab.5 Results of the system when epoch length is 23.6 s %

为了验证训练集和测试集在数据独立状态下系统的性能,将实验数据先随机划分成训练集和测试集,然后再对训练集和测试集中的数据段截断成epoch,其长度分别为5.9 s和23.6 s,分别测试其精度。表6给出训练集和测试集数据在3种不同随机组合(Group 1、Group 2、Group 3)时的分类精度。

表6 随机数据组合时系统精度Tab.6 Accuracy of the system using randomized data

从表6可见,样本长度为23.6 s的分类精度也可高达100%。

表7给出了本文与其他部分文献在分类精度,二分类及三分类类型,研究方法方面的对比。从表7看出,本文实验结果优于现有其他文献性能。文献[7]采用遗传算法及SVM,其精度、特异性、敏感度也可高达100%,但仅用于正常与癫痫发作EEG信号分类识别。本文研究方法可用于正常、癫痫发作及发作间期EEG信号自动检测,具有高性能特点,为癫痫及癫痫发作的临床检测提供了较好的参考价值。

表7 本文与其他文献的对比Tab.7 Comparison with previous works

4 结束语

本文提出了一种基于二叉树多分类SVM的癫痫及癫痫发作的高性能自动检测系统。该系统能实现自动检测正常、癫痫发作和发作间期EEG信号;采用多级提升式小波变换将EEG信号分解为不同幅频特性的子带信号,求得不同子带信号的特征量;为了减小特征维度,采用Fisher得分法对特征量进行排序并筛选具有较高分类精度的特征量,利用基于MSMO的二叉树多分类SVM算法对3种类别EEG样本数据进行分类识别。实验结果表明,针对德国波恩大学的正常、癫痫发作和发作间期EEG信号数据集,该系统的精度、敏感度和特异性均可达100%,优于现有的分类识别方法,可为医生对癫痫患者的临床检测提供较大的帮助。