可重构智能表面辅助大规模MIMO通信波束成形设计
王 丹,王勇芳,陈小梦,郑明杰,杜亚东
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引 言
与无线网络中使用的其他技术相比,可重构智能表面(reconfigurable intelligent surface,RIS)的最大优势在于可以控制无线电波的散射、反射和折射特性从而减小无线传播的负面影响。RIS的特点:几乎无源,在理想情况下,不需要外加任何电源;没有射频链,不需要模数/数模转换器和功率放大器,在反射信号时不会放大或引入噪声;可用于全双工传输;便于部署等。因此,RIS被视为6G大规模多输入多输出(multiple input multiple output,MIMO)的潜在技术之一[1]。
基于RIS的无线中继波束成形设计是目前RIS在移动通信领域的主要研究方向之一,通过对电磁信号进行重新定向和波束赋形,能更高效地运用信号能量,提高无线信道性能[2]。在大规模MIMO系统中,波束成形技术主要有数字波束成形[3]、模拟波束成形以及混合波束成形。数字波束成形可以得到很好的系统性能,但由于MIMO系统中有很多天线,并且需要给每个发射天线配置一条射频链,导致硬件成本以及能耗升高,使得纯数字波束成形很难得到应用。而模拟波束成形只使用一条射频链,在经济上成本更低,但是模拟波束成形缺乏对信号幅度的控制,并且只支持一条数据流进行传输,不能实现复用。数模混合波束成形能够同时得到数字波束成形和模拟波束成形的优点,使用比数字波束成形少的射频链,同时能够实现多数据流传输,从性能上看,其信道增益小于数字波束成形但远高于模拟波束成形。鉴于混合波束成形技术能够在硬件复杂度和系统性能之间作出一个有效的折中[4],因此,混合波束成形的设计更加重要。
文献[5]将奇异值分解(singular value decomposition,SVD)应用在MIMO的线性数字波束成形中,实现了各子信道之间相互正交,分解后得到的奇异值矩阵是一个对角矩阵,使得接收端的检测算法简单,容易实现;缺点是SVD分解会得到信噪比差距很大的多个子信道,较差的子信道需要分配更多的功率,使得不同子信道需要使用不同的调制解调方案,需要使用“注水算法”[6]进行功率分配,同时,“注水算法”可能会进一步加剧不同子信道之间的差异。因此,从实际角度看,SVD波束成形方案并不是最优的。文献[7]使用统一信道分解(uniform channel decomposition,UCD)方案设计了MIMO系统在总平均功率约束下的预编码器,使得信道分解为几个相互正交且信道增益相同的并行子信道,不同子信道之间可以使用不同的调制解调方案。
在混合波束成形中主要有2种设计思路:第1种思路是利用MIMO信道的稀疏性进行发送端和接收端矩阵的交替优化,首先找到发送端局部最优解,更新矩阵方程求解得到此时接收端组合器最优矩阵,逐步迭代得到收发两端4个矩阵的最优解,缺点是需要多次迭代,收敛速度慢。文献[8-9]就是在此思路上分别运用黎曼流形优化和梯度投影法进行混合波束成形的设计;文献[10]中的正交匹配追踪(orthogonal matching pursuit,OMP)方法也是该思路;文献[11]在OMP算法上加入了SVD,先使用OMP进行混合预编码的求解,再使用SVD进行混合组合器的求解。第2种思路是先联合求得发送端和接收端的模拟域矩阵,将结果放入信道中构成等效基带信道,然后基于某种性能最优化得到数字域矩阵,这种算法能够将问题转化为对模拟域和数字域的分别求解,实现了数模两域的解耦,计算数字域矩阵时不需考虑模拟域的相移元素的恒模约束,降低了优化难度。文献[12-15]就是根据这种思路进行波束成形矩阵的设计。
本文结合以上2种思路进行波束成形设计。首先利用第1种思路中接收端和发送端之间交替迭代优化的方式,使用改进的OMP方法只进行模拟域矩阵的设计,再利用第2种思路将得到的模拟域矩阵放入信道中构成等效信道矩阵,基于此等效矩阵使用UCD实现收发两端数字域矩阵优化设计,从而弥补子信道之间的性能差异和容量损失。此方案使用第1种思路进行模拟域2个矩阵的迭代优化,而不是收发两端4个矩阵的迭代,同时,使用等效基带信道进行数字域的设计,实现了数模解耦,各子信道之间相互正交,能够使用统一的调制解调方案,减少了迭代过程和子信道之间的性能差距。
在RIS的相位优化中,假设已知完美信道状态信息(channel status information,CSI)[16-19],使用信道中相关的到达角(angle of arrival,AoA)和离开角(angle of departure,AoD)进行RIS相位优化设计,得到RIS阵元相位的显式解。
仿真结果表示,即使不使用任何纠错码,不需要复杂的功率分配,在信噪比较高且支持不同数据流条数时,提出的RIS辅助通信混合OMP UCD波束成形方案的误比特率(bit error rate,BER)性能和频谱效率优于其他波束成形方案;证明了RIS部署的反射天线阵元个数越多,信道性能越好。

1 系统模型
图1是RIS辅助大规模MIMO通信的全连接混合波束成形模型,该系统是一个RIS辅助的单用户毫米波(millimeter wave,mmWave)MIMO系统中的下行通信链路。考虑到mmWave频段拥有丰富的带宽资源[20],本文借助正交频分复用(orthogonal frequency fivision multiplexing,OFDM)技术的抗多径干扰特性[21]对RIS辅助通信的混合波束成形进行研究。需要优化的是基站端的混合预编码矩阵、用户端的混合组合器矩阵以及RIS相位矩阵。

图1 系统模型Fig.1 System model

基站端导频信号s(k)∈Ns×1经过数字预编码、模拟预编码处理后通过信道传输到用户端,因此,到达用户端的第k个子载波的信号可以表示为
x(k)=H(k)FRFFBB(k)s(k)+n(k)∈N×1
(1)

假设用户与基站之间的直接链路被堵塞,则第k个子载波的等效信道表示为
H(k)=HUR(k)ΦHRB(k)∈N×M
(2)
(2)式中:HUR(k)∈N×R为用户端与RIS之间的信道;HRB(k)∈R×M是RIS与基站之间的信道;Φ∈R×R是RIS反射矩阵,它是一个对角矩阵,其对角元素是RIS的阵元响应。

(3)
需要说明的是,本文假设基站端和用户端可以实时获取信道状态信息,即矩阵H是已知的。
2 信道模型
毫米波的宽频带、窄波束和短波长特点导致了其在空间传播中的严重路径损失,因此,毫米波主要通过视距(line of sight,LoS)以及少量的一次反射引起的非视距(non line of sight,NLoS)进行传播,导致毫米波的信道是稀疏的,因此,考虑使用基于Saleh-Valenzuela[22]模型的方法进行建模,这种信道利用信号在空中传播的多径特点,通过对每一个子径的功率和角度进行描述,将各子径信道叠加来构建信道模型。
Saleh-Valenzuela模型将角度分布近似、时延接近的多条传播路径归为一个簇,结合上述毫米波的传输特点将信道建模为一条LoS路径与Nc条NLoS散射簇,每条散射簇包含Np条传播路径,时域模型可以表示为
(4)
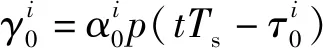
(5)

第k个子载波的频域信道模型可以表示为
(6)
(6)式中:T为时延抽头个数;K为子载波数量;k=1,…,K。
3 优化目标
该系统的频谱效率可以表示为
(7)
|FRFi,j|=1,∀i,j
|WRFi,j|=1,∀i,j
|Φn,n|=1,n=1,…,R
(8)

本文的混合波束成形优化目标可以转换为在Frobenius范数的度量下寻找一对足够接近全数字SVD波束成形矩阵的混合预编码器和混合组合器。为了解决这个问题,首先对信道矩阵H(k)进行SVD分解得到数字波束成形矩阵的最优解,表示为
H(k)=Wopt(k)Γ(k)Fopt(k)H
(9)
(9)式中:Wopt(k)表示H(k)的左奇异矩阵,维度为N×Ns,是混合组合器的最优解;Fopt(k)表示H(k)的右奇异矩阵,维度为M×Ns,是混合预编码器的最优解;Γ(k)表示一个维度为Ns×Ns的对角矩阵,其对角元素为降序排列的奇异值。
因此,FRF和FBB(k)的优化目标表示为
|FRF i,j|=1,∀i,j
(10)
同样,WRF和WBB(k)的优化目标可以表示为
s.t.|WRF i,j|=1,∀i,j
(11)
4 优化方案
本节主要讨论预编码器的设计,提出的算法同样可以应用于组合器。
4.1 模拟预编码/组合器优化设计
优化目标是一个含有非凸约束的多元优化问题,要想得到这种有约束多元优化问题的全局最优解是非常困难的,文献[11]中的OMP方法是一种稀疏波束形成方法,得到的是次优解。

(12)
算法1改进的OMP算法过程
步骤1 初始化:FRF=0,Fres(k)=Fopt(k)
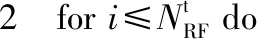


步骤5FRF=[FRF|At(:,l)]


步骤8 end for
步骤9 returnFRF

4.2 数字预编码/组合器优化设计
4.1节已经得到了模拟预编码器FRF与模拟组合器WRF,本节将根据FRF、WRF与信道信息来设计数字预编码/组合器。在已知FRF的情况下,数字预编码的优化问题可以重写为
(13)

(14)

(15)
由UCD方法得到的数字预编码矩阵为
(16)
Ω(k)∈Ns×Ns,满足Ω(k)HΩ(k)=I,这样保证了预编码矩阵FBB(k)仍然满足子信道之间相互正交,下面来阐述怎样得到Ω(k)。
若给定数字预编码矩阵FBB(k),则
(17)
G(k)的增广矩阵为
(18)
UCD方案的依据:对于(18)式的矩阵Ga(k)能够进行正交三角分解,得到一个半酉矩阵QG(k)和一个对角线元素相等的上三角矩阵RJ(k)使得G(k)=QG(k)RJ(k)。
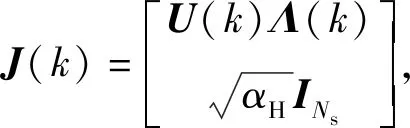
(19)
(19)式中,Σ(k)是一个Ns×Ns的对角矩阵,其对角元素为
(20)
对Σ(k)进行几何均值分解,得到
Σ(k)=Q(k)RJ(k)P(k)H
(21)
(21)式得到的Q(k)和P(k)都为酉矩阵,此时,Ω(k)=P(k)H,QG(k)=U(k)Λ(k)Σ(k)-1Q(k),G(k)=U(k)Λ(k)Σ(k)-1Q(k)RJ(k),因此,得到的数字域预编码矩阵为
FBB(k)=V(k)P(k)
(22)
数字域组合器矩阵为
(23)
4.3 RIS相位优化设计
在FRF、WRF、FBB(k)与WBB(k)已知的情况下,(8)式表示的优化目标为
s.t.|Φn,n|=1,n=1,…,R
(24)
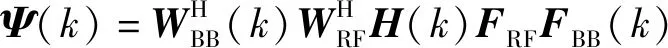
|Φn,n|=1,n=1,…,R
(25)

(26)
(26)式中,根据信道模型,有
(28)

s.t.|Φn,n|=1,n=1,…,R
(29)
由上述推导可以得到RIS的第n个元素的解为
(30)

(31)
本文是在假设已知CSI的情况下设计的RIS相位,实际中,由于RIS由大量的无源反射元素构成,信道估计的训练开销是很大的。本文只利用了RIS-用户的AoD和基站-RIS的AoA来设计RIS反射系数矩阵。相关的AoA和AoD可以通过先进的角度估计方法得到。
5 复杂度分析
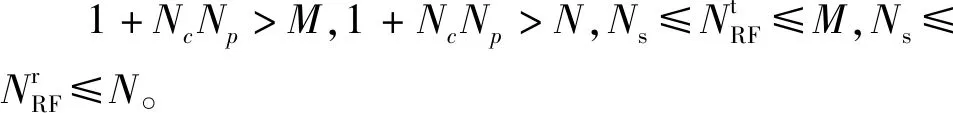


第3部分来自RIS相位优化设计,求解Z的计算复杂度为O(R2),求解Φn,n的计算复杂度为O(R)。

6 仿真结果
本节对提出的RIS辅助通信混合OMP UCD波束成形方案的BER和频谱效率性能进行分析。所提混合波束成形方案的仿真参数设置如表1所示。
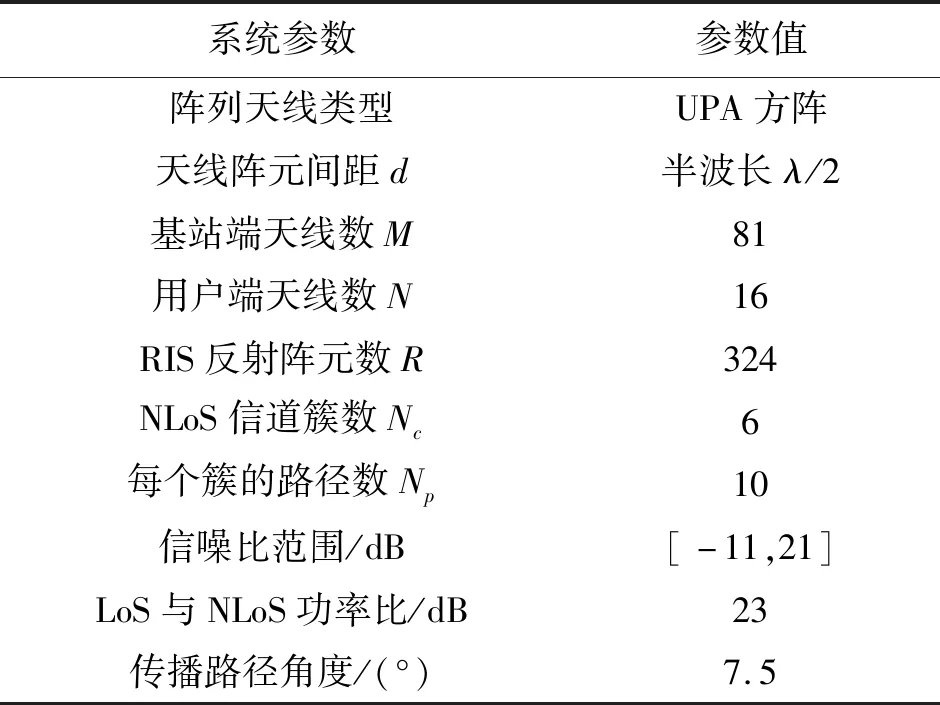
表1 仿真参数Tab.1 Simulation parameters
图2展示了所提出的混合OMP UCD波束成形方案的BER性能,并将其与数字SVD、UCD以及混合OMP SVD波束成形方案进行对比。

图2 全数字波束成形与混合波束成形的BER性能Fig.2 BER performance between digital beamforming and hybrid beamforming
图2中2种混合波束成形中的模拟预编码器使用的都是OMP方法,从图2可以看出,在信噪比为[-11,21] dB时,无论是全数字UCD还是混合OMP UCD,其在BER性能上的表现都是优于SVD的,这是因为基于UCD的波束成形方案能够形成几个相等的子信道,能够缓解由于某个子信道性能不好而对整个系统性能的恶劣影响,当信噪比为13 dB时,基于SVD的全数字波束成形的BER为7.43×10-3,而该方案的BER为3.28×10-4。
图3为信道中部署的M、N和R相同时,支持的数据流条数不同引起的BER变化。

图3 支持数据流不同时的BER性能Fig.3 BER performance when data streams are different
从图3可以看出,当信道的阵列元素个数相同时,系统支持的数据流数越多,BER就越大,这是因为数据流越多,波束成形系统的维数就越大,从而导致BER增大。
基站和用户端的天线阵元数相同时,部署不同的RIS反射阵元个数对提出的混合OMP UCD波束成形方案的BER的影响如图4所示,此时系统支持的数据流都控制为3。

图4 RIS反射阵元个数不同时的BER性能Fig.4 BER performance when the number of RIS reflection array element is different
由图4可知,在其他条件相同时,通过设计RIS反射矩阵,能够获得比没有RIS辅助通信更好的BER性能,部署在RIS上的反射阵元越多,该混合波束成形系统的BER性能越好,但同时会造成更大的时延,因此,在信道快速变化的系统中,RIS部署天线的个数还需要进一步研究。
在基站和用户端的天线阵列数相同时,有无RIS的部署对提出的混合OMP UCD波束成形方案频谱效率的影响如图5所示。

图5 不同波束成形方案下的频谱效率性能Fig.5 Spectral efficiency performance of different beamforming schemes
从图5可以看出,混合OMP与SVD方案和混合OMP与UCD方案的频谱效率一样,这是因为SVD和UCD得到的数字预编码和组合器矩阵都是酉矩阵,频谱效率只与模拟域矩阵有关;本文所提出的混合OMP与UCD方案的频谱效率比混合主成分分析(principal component analysis,PCA)与UCD方案和黎曼流形算法的频谱效率高。还可以看出,RIS的相位设计方案可以使得频谱效率性能更好,这是因为该RIS相位设计方案能够有效地利用信道角度特性来提高信道质量和传输性能。
在基站和用户端的天线阵列数相同时,传输数据流条数对3种不同的波束成形方案频谱效率的影响如图6所示。
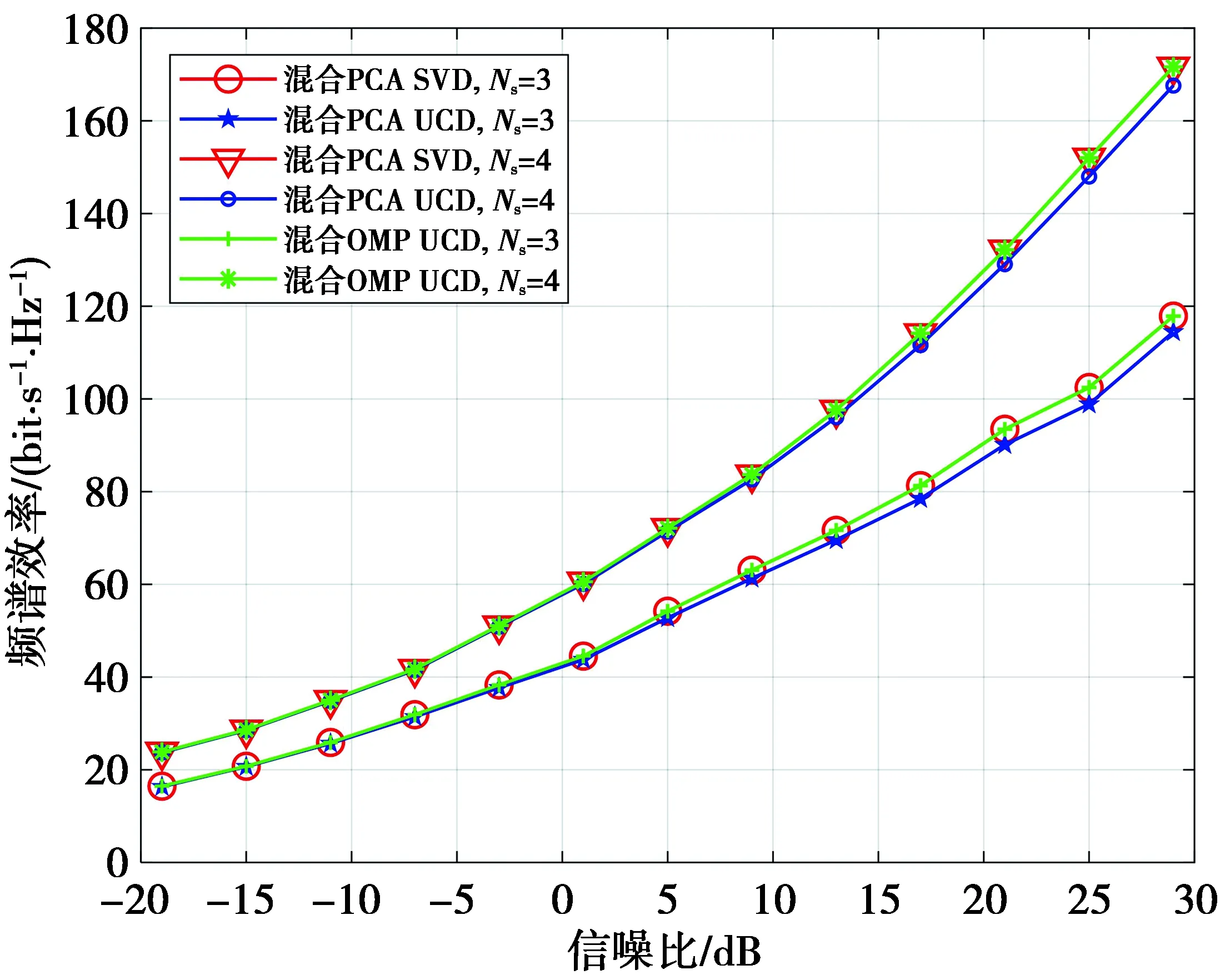
图6 传输不同数据流对频谱效率的影响Fig.6 Influence of transmitting different data streams on spectral efficiency
从图6可以看出,传输数据流Ns=4时的频谱效率整体比Ns=3时的频谱效率高,这是因为数据流越大,混合波束成形方案越接近全数字波束成形方案,但也会导致功率消耗增大等问题,所以在实际系统中对数据流数目的选取应进行综合考虑。
在设计RIS阵元相位时只考虑LoS路径和考虑所有路径时4种混合波束成形方案在不同信噪比下的BER性能如图7所示,整体上可以看出,考虑全部路径时比只考虑LoS路径的BER性能稍好,这是因为NLoS路径的信道增益远小于LoS路径,其对信道性能的提升有限。因此,在设计RIS相位时为了降低复杂度只考虑了LoS路径。

图7 设计RIS时考虑所有路径或LoS路径对BER的影响Fig.7 Influence of all paths or LoS path on BER when designing RIS phase
7 结束语
本文提出了一种RIS辅助大规模MIMO通信系统的混合OMP UCD波束成形方案。将数模两域的预编码器和组合器进行解耦,对于模拟域部分,使用OMP算法将问题转化为多元稀疏信号重构问题;对于基带数字域部分,不需要进行逐步迭代,不使用复杂的功率分配方法,使用UCD将信道分解成Ns个性能相同的子信道。此外,本文根据基站—RIS,RIS—用户之间信道的AoA和AoD,得到了RIS阵元相移的显式解。通过仿真证明了该RIS辅助通信波束成形方案能够得到良好的系统BER性能和频谱效率。

