基于燃油经济性的坡道适应性巡航控制研究

唐荣江,李蒙康,毕道坤,张致远,周辉

(1.桂林电子科技大学机电工程学院,广西 桂林 541004;2.吉林大学汽车工程学院,吉林 长春 130012;3.东风柳州汽车有限公司商用车技术中心,广西 柳州 545005)

商用车作为货物运输的重要途径,在生产生活中占据越来越重要的地位,在以降低能源消耗和环境保护为主题的时代,提升燃油经济性成为商用车领域主要研究方向之一[1]。

适应性巡航控制由定速巡航发展而来,主要以安全性与舒适性为主要研究热点[2]。我国地形以山地丘陵居多,起伏的道路势必导致车辆燃油消耗的提高,研究表明,相比平坦道路,在丘陵地区车辆的燃油消耗要高出5%～20%[3]。车辆通过坡道路面时,车辆的燃油经济性不仅与自身运行状态密切相关,且在很大程度上还与驾驶员对车辆的操作行为有关,不合理的加速、减速都会造成油耗的增加[4]。因此,考虑坡道信息的适应性巡航控制,对提升商用车的燃油经济性有重大意义。

Erik Hellström[5]基于最优巡航控制开发了预测性经济巡航速度控制器,借助车载GPS系统和坡度数据库获得道路几何信息,将此前瞻性信息用于预测性优化速度轨迹,该经济巡航控制系统既保证了乘客舒适度,也降低了车辆燃油消耗量。周敏[6]对自动变速巡航控制的汽车在通过坡道路面时的整车燃油经济性进行研究,采用动态规划算法规划了车辆在坡道上行驶的最合理速度轨迹,通过仿真验证,所提出的考虑坡道的巡航控制大幅度提升了车辆燃油经济性指标,同时充分保证驾驶时间和舒适度。D.Jia[7]提出一个增强的PCC系统,集成了数据驱动的流量预测模型和瞬时控制算法,计算瞬时最佳速度曲线,以最小化能量消耗行驶。Y.Lin[8]基于全球定位系统(GPS)和地理信息系统(GIS)提出基于上下坡道路的经济巡航控制系统,将数字道路地图的道路高程剖面与非线性预测控制策略相结合,根据道路等级提供经济速度,不仅可以为驾驶员提供经济驾驶指导,还可以实现驾驶安全。

车辆纵向运动具有非线性、时变性和不确定性等特点,研究对象为“人—车—环境—任务”的多元耦合系统。本研究提出了一种基于道路地形信息、车辆动力学模型和燃油消耗模型的非线性预测控制的坡道适应性巡航控制方法,在确保车辆行车安全性的前提下,提高车辆的道路适应能力,避免车辆频繁的加速和减速行为,实现车辆的纵向自动控制,提高燃油经济性。

1 适应性巡航控制系统总体方案

车辆行驶过程中,在没有横摆运动的前提下,仅需要对车辆纵向运动进行控制,采用经典的上下层控制结构。上层控制系统通过车辆运行状况和当前行驶的道路工况,基于极小值原理对快速优化的非线性模型预测控制算法进行求解,以最优控制变量的求解方程获得前方道路坡度的纵向需求扭矩的最优控制序列,输出车辆的期望扭矩给下层控制系统。下位控制系统运用逆纵向动力学模型输出期望油门开度α,利用油门开度控制车辆纵向动力学模型,控制加速或减速,实现车辆坡道适应性巡航控制系统的功能。坡道适应性巡航控制系统总体方案见图1。

图1 适应性巡航控制系统的总体方案

2 车辆系统建模

2.1 道路工况

考虑到仿真工况的普遍适用性,参考我国的实际地形特点,尤其南方一些丘陵地带的典型道路,常伴随有一定的坡度,并根据国家道路标准,道路坡度设计的极限值范围在-10%～10%之间。利用TruckSim动态系统仿真软件,搭建虚拟道路工况,模拟真实的行车工况进行仿真,采用两种仿真工况进行仿真分析：一种场景为正弦函数模拟典型的单一上坡道路、上下坡道路工况;另一种场景选取柳州到贵港高速公路其中一段的真实道路作为研究工况。

2.2 纵向动力学模型

对车辆纵向动力学进行分析,可建立纵向动力学方程,其表达为

(1)

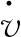
驱动力由发动机扭矩提供,其表达式为

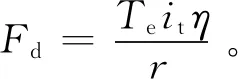
(2)

式中：Te为发动机的输出扭矩;it=ig·i0,为传动系统总变速比;η为传动系效率;r为轮胎半径。

坡道阻力为

Fi=mgsinα。

(3)

式中：g为重力加速度;α为道路坡度。

空气阻力为

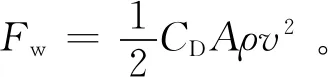
(4)

式中：CD为空气阻力系数;A为迎风面积;ρ空气密度;v为车速。

滚动阻力为

Ff=fmgcosα。

(5)

式中：f为滚动阻力系数。

2.3 燃油消耗模型

车辆在道路上行驶时,建立满足非稳定工况的瞬态油耗预测模型,准确估计车辆在稳定和非稳定工况下的燃油消耗。基于瞬态修正的多项式油耗模型建模思路,利用多项式油耗模型对燃油消耗率与扭矩和发动机转速之间的关系线性建模,并利用瞬态燃油变量对稳态模块进行修正。

建立稳态油耗模型,其表达式为

mf=f(ne,Te)=b1+b2ne+b3neTe+b4ne2Te。

(6)

式中：mf为稳态燃油消耗率;b为油耗模型参数;ne为发动机转速。

分析燃油消耗的差值与发动机扭矩变化率之间的关系,发现燃油消耗差值与发动机扭矩变化率基本呈线性关系,其表达式为

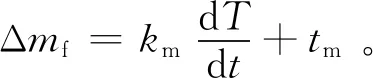
(7)

式中：Δmf为燃油消耗差值;km,tm为待定系数。

综合瞬态修正模块和稳态油耗模型,建立瞬态修正的多项式燃油消耗模型,其表达式为

(8)

图2 燃油消耗率拟合图

通过实车试验,分析采集的油耗数据,利用最小二乘法,拟合燃油消耗模型,选取其中预测精度最优的模型为本研究油耗模型。燃油消耗率的拟合性能见图2。

3 适应性巡航控制系统的设计

车辆行驶过程中,实际道路工况千变万化,坡道适应性巡航控制应具备合理控制巡航需求扭矩的能力。适应性巡航控制采用分层控制结构,上层控制系统结合前方道路工况和相关车辆信息进行分析,规划出车辆需求发动机扭矩;下层控制系统通过车辆逆纵向动力学模型输出期望油门开度,由油门控制器实时控制车辆。

3.1 上层控制系统设计

3.1.1 系统方程建模

车辆建模仅考虑车辆的纵向运动,假设与其他车辆没有相互作用。建立被控系统的纵向控制模型,假设车辆在任何时刻t的状态方程为

(9)

式中：x,u分别为控制系统的状态量和控制量。

车辆发动机扭矩与控制输入有关,即Te(t)=u(t);x(t)=[x1(t),x2(t)]T,x1,x2分别为主车辆t时刻的当前位置与速度。

改写车辆的状态方程为

(10)

车辆加速和减速与发动机扭矩的变化直接相关,为了考虑巡航控制系统中的平顺性问题和驾驶员行为的任何异常,重新定义与控制输入相关的不等式约束,引入虚拟输入ud,表示为

(11)

为了优化车辆控制输入,解决最优控制问题,则需建立性能指标函数,评价控制效果优劣。其表达式为

(12)

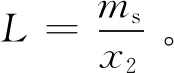
(13)

式中：成本函数L为车辆单位距离所消耗的燃油量。

利用拉格朗日乘子法推导最优控制输入,并引入哈密顿函数：

H(x,λ,u,ψ)=L(x,u)+λTf(x,u)+ψTC(x,u)。

(14)

式中：λ为协态因子;ψ为与约束相关的拉格朗日乘子。

3.1.2 最优控制离散化

滚动时域控制本质上是一系列连续时间内的时域最优控制问题。将预测范围T分为N个步骤,步长为Δt=T/N,其中i=0,…,N-1表示所述预测视界中第i个实例处的相应值。

电子地图能够预知前方道路信息,利用前向欧拉方法对任意位置的道路坡道角θ离散计算,其表达式为

(15)

式中：θ(x1)为第i阶段道路坡道角;hi与hi+1分别为第i阶段与第i+1阶段的海拔;xi与xi+1分别为第i阶段与第i+1阶段的位移。

离散化最优控制问题可以表述如下：

minimize：

(16)

Subject to：

xi+1(t)=xi(t)+f(xi(t),ui(t))Δt。

(17)

上述离散化非线性代数方程,基于隐函数的离散极小值原理,对离散化最优控制问题进行求解,将泛函条件极值问题转化为无约束的泛函极值问题,可得到广义泛函极值的必要条件。

x(t),λ(t)需要满足的边界可以表述如下：

x(t0)=x0,

(18)

(19)

最优控制的必要条件可以概括如下：

Hu(xi(t),λi(t),ui(t),ψi(t))=0,

(20)

(21)

3.2 下层控制系统设计

汽车在行驶过程中,其输出扭矩与油门开度、发动机转速有关,通过TruckSim软件提取发动机的MAP图(见图3)。

由发动机MAP图构建发动机扭矩、转速与油门开度的对应关系：

α=f(ne,Te)。

(22)

式中：α为油门开度;f(ne,Te)为逆发动机扭矩特性曲线。若通过车辆的状态和当前道路工况得到发动机期望扭矩Te和发动机转速ne,则可通过二维查表法得到此工况下对应的期望油门开度。

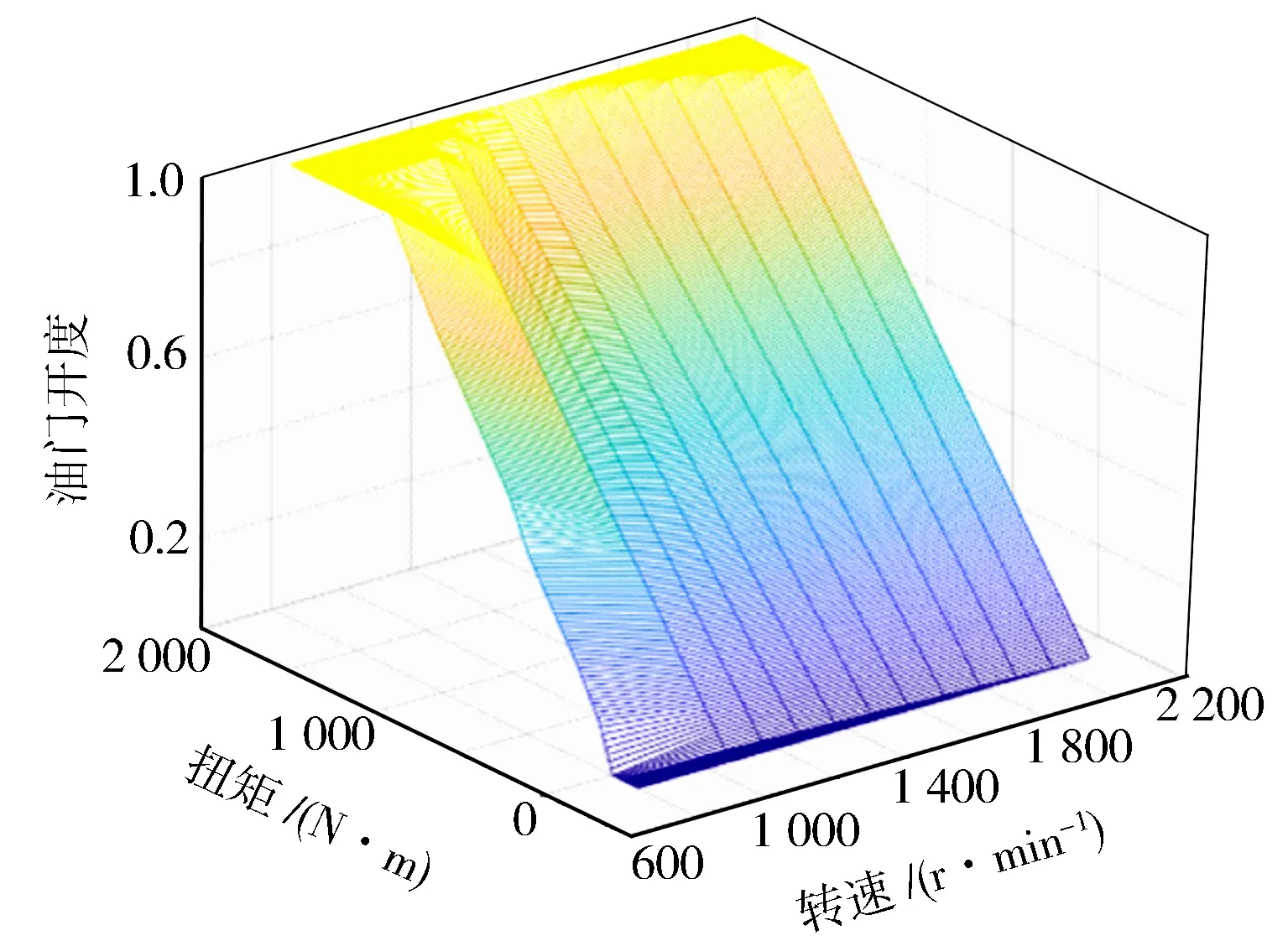
图3 发动机MAP图

4 联合仿真

MSC TruckSim是动态模拟整车动力学仿真软件,从人、车、路、项目、事件等多个方面入手,对基本的各项试验进行仿真,从而分析车辆的各项性能。搭建整车模型,设置驾驶员行为和道路行驶工况、行驶路面条件、输入输出信号、仿真时长和频率,导入Simiulink中得到联合仿真的车辆模型。在TruckSim软件中设置车辆的主要参数,如表1所示。在Matlab/Simulink平台上搭建的商用车坡道适应性巡航的联合仿真模型见图4。

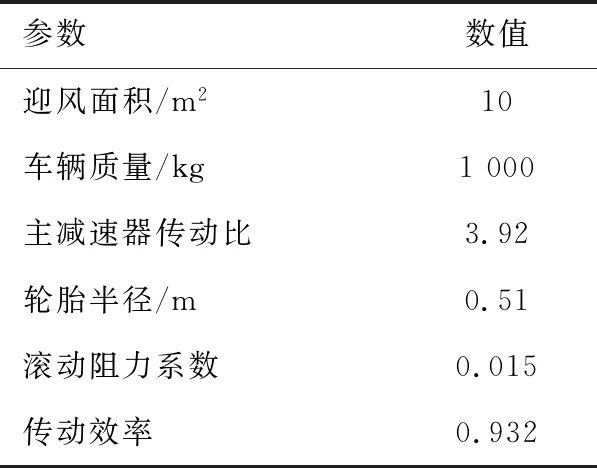
表1 车辆主要参数

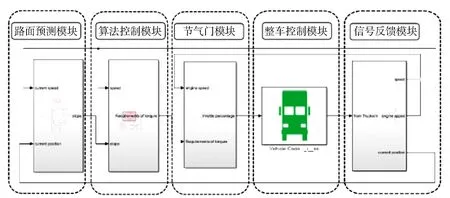
图4 Simulink与TruckSim联合仿真模型

5 系统仿真验证

为了进一步评估所提出的坡道适应性巡航控制的节能性能,建立虚拟道路仿真工况,分别在单一上坡道路工况、上下坡道路工况、真实道路工况进行联合仿真试验。车辆的初始巡航速度设定为75 km/h。

5.1 上坡道路工况仿真

在总长度1 200 m、最大坡度4.5%的单一上坡道路工况进行联合仿真,结果见图5。

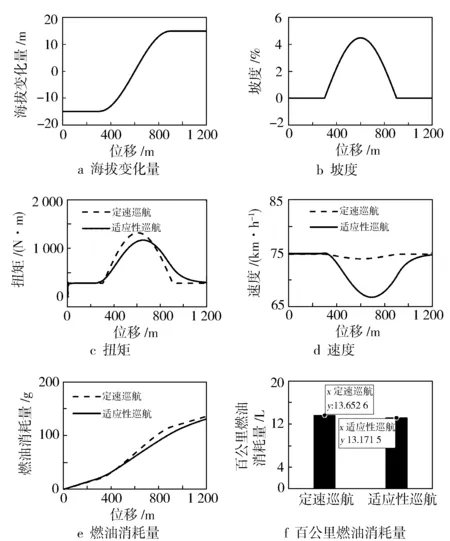
图5 上坡工况仿真结果

海拔变化范围为-15～15 m,坡度范围为0%～4.5%,由需求扭矩变化曲线可知,车辆在上坡前需求扭矩增大,适应性巡航控制车辆在上坡路段前发动机提高扭矩,积蓄能量,上坡过程中根据车辆前方道路坡度的大小,使发动机工作在燃油经济性最优扭矩。比较速度变化曲线可知,定速巡航一直稳定在规定速度行驶,适应性巡航速度随坡度的改变而变化。由图5e知,定速巡航的总燃油量为135.98 g,适应性巡航的总燃油量为131.19 g,适应性巡航的燃油消耗量增长缓慢。通过比较图5f百公里燃油消耗量可知,坡道适应性巡航控制比定速巡航控制节省约3.52%的燃油。

5.2 上下坡道路工况仿真

上下坡道路工况的联合仿真道路总长度为2 400 m,最大坡度为2.5%,仿真结果见图6。

由图6可知,海拔呈正弦函数变化,在上下坡道路工况中,选取海拔变化范围为-7.5～7.5 m,坡度范围为-2.5%～2.5%。由图6c知,在进入下坡前,需求扭矩降低,提前轻微减小油门开度,进入下坡时,使其车辆稳定工作在燃油经济性最优扭矩,利用下坡优势和动能与重力势能转换,减少了能量损耗。由图6e知,定速巡航的总燃油量为169.027 g,适应性巡航的总燃油量为164.587 g。图6f为百公里燃油消耗量的比较,提出的坡道适应性巡航控制算法比定速巡航控制节省2.62%的燃油。

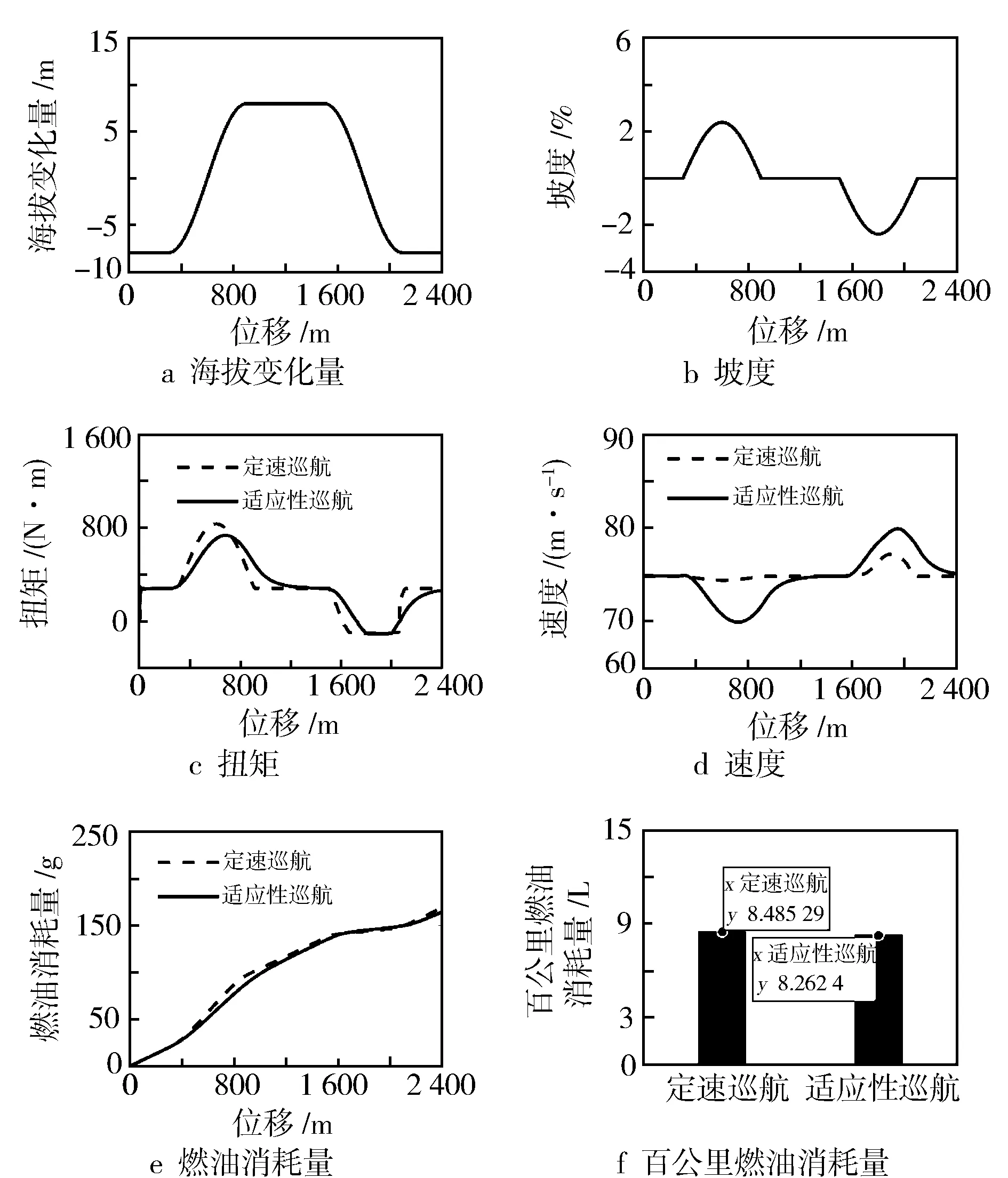
图6 上下坡工况仿真结果

5.3 实际道路工况仿真

作为对比验证,基于实际道路评估所提出的坡道适应性巡航控制系统的有效性。选取柳州到贵港的一段真实道路,长为3 000 m,比较结果见图7。

真实道路的坡度范围在-4%～2.2%。由图7可知,定速巡航的总燃油量为205.323 g,适应性巡航的总燃油量为199.5 g,通过比较百公里燃油消耗量,可知提出的坡道适应性巡航控制算法比定速巡航节省约2.84%的燃油。

图7 真实道路工况仿真结果

6 结束语

提出了商用车坡道适应性巡航控制的燃油经济性仿真模型,研究车辆在稳定和非稳定工况下的燃油消耗模型、坡度变化、行驶工况对燃油经济性的影响。针对坡道巡航的燃油经济性问题,基于Trucksim和Simulink软件对开发的坡道适应性巡航控制系统进行联合仿真并验证。从仿真结果可知,在上坡前,车辆通过提前输出油门开度,积蓄能量,避免上坡过程中出现急减速;进入下坡时,在没有任何制动的情况下,提前减少油门开度,利用下坡的优势,充分利用动能与重力势能转换,减少能量损耗。

在虚拟道路仿真工况和真实道路仿真工况下,与传统定速巡航控制相比,坡道适应性巡航控制平均节油效果达到约3%,有效降低了燃油消耗量。