考虑温度和燃油稀释的柴油机润滑油黏度模型研究
王天齐,王亚宁,张斌,田晔,刘晓日
( 1.河北工业大学能源与环境工程学院河北省动力系统污染物控制技术创新中心,天津 300401;2.清华大学天津高端装备研究院润滑与摩擦检测中心,天津 300300;3.浙江大学生物系统工程与食品科学学院,浙江 杭州 310058)
国六排放标准对柴油机排气污染物的要求更加严格,尤其限制了氮氧化物(NOx)和颗粒物(Particulate Matter,PM)的排放。为了应对法规要求,各种先进的燃油喷射技术逐渐普及,其中燃油后喷技术不需要额外添加设备,而且可以同时降低NOx和PM排放,因而得到广泛应用。但燃油后喷会造成油束喷射至缸套壁面,最终被活塞环带入到油底壳里的润滑油中,随着时间的累积导致润滑油被稀释[1],从而引起润滑油液黏度由于燃油稀释而非正常下降[2-3]。
黏度是润滑油最重要的特性参数,当前润滑计算中黏度通常通过试验或者黏温方程得到。黏温方程主要有Vogel方程、Andrade方程和Reynolds方程等[4-5],广泛应用于活塞组、主轴承和连杆轴承等内燃机零部件的润滑仿真计算[6-9]。燃油稀释润滑油导致黏度降低,这会对内燃机摩擦副的摩擦和可靠性造成显著影响[10-12],而燃油稀释在不同温度下对黏度的影响程度和规律尚不清楚。
传统黏温方程是随温度变化的曲线,只能计算曲线上某一点的黏度数值,而不能同时体现温度和燃油稀释两个参数影响。对于多个参数的黏度预测模型,Loh[13]利用神经网络模型预测不同配方的润滑油黏度,得到了准确的预测结果,Esfe[14]根据操作温度和固体颗粒的含量预测ZrO2-MWCNT (70%~30%)/10W40杂化纳米润滑油的黏度,Karunarathne[15]根据CO2的浓度和温度预测含水胺混合物的密度和黏度。当前使用神经网络算法预测润滑油黏度的研究较少,而在内燃机领域考虑温度和燃油稀释的神经网络黏度预测模型更需要进一步研究。
本研究以美孚15W-40柴油机润滑油为例,通过测试获得原润滑油和掺混不同体积分数燃油后润滑油在20~180 ℃的黏度,拟合获得Vogel,Andrade和Reynolds黏温方程,并比较分析拟合效果。定义稀释黏度比,构建稀释黏度比-温度方程,以此反映燃油稀释在不同温度下对黏度的影响程度和规律。构建了基于润滑油温度和燃料体积分数的反向传播(Back Propagation,BP)神经网络黏度模型,实现了对20~180 ℃温度范围以及0%~15%燃油体积分数范围内任意一点黏度的预测。
1 黏度试验测试
在清华大学天津高端装备研究院润滑与摩擦检测中心使用Anton Paar EC-Twist302旋转流变仪(见图1)测量润滑油黏度。

图1 EC-Twist302旋转流变仪
试验选用了美孚公司15W-40柴油机润滑油,通过在润滑油中混入不同体积分数的燃油以模拟发动机实际工作过程中润滑油发生的燃油稀释现象,燃油体积分数分别为3%,6%,9%,12%,15%,油样测试的温度区间为20~180 ℃,试验得到黏度随温度和燃油体积分数变化的数据,黏温曲线如图2所示。

图2 15W-40润滑油在不同燃油体积分数下的黏温特性曲线
由图2可见,15W-40润滑油的黏度随温度的升高而变小,温度低时润滑油黏度变化较快,高温时黏温曲线趋于稳定。当燃油体积分数φ改变时,黏度随温度变化的趋势不受其影响,仍为指数型下降,只是黏度曲线整体随燃油体积分数增大出现下移趋势。
2 燃油稀释与黏温方程
2.1 Vogel方程、Andrade方程和Reynolds方程
选用Vogel方程、Andrade方程和Reynolds方程对15W-40润滑油黏度-温度数据进行拟合,以比较和确定更适用于燃油稀释的黏温模型。
Reynolds方程形式为
lnu=lnu0-D(T+273 ℃)。
(1)
式中:u为润滑油动力黏度;u0为参考温度下的动力黏度;T为温度;D为常数;可令C=lnu0,看作常数处理即可。
经过处理,Reynolds方程为
lnu=C-D(T+273 ℃)。
(2)
Andrade方程形式为
lnv=A+BT-1+CT-2+DT-3。
(3)
式中:v为润滑油的运动黏度;T为温度;A,B,C,D均为与润滑油种类有关的待确定常数。对于Andrade方程,为了提高关联精度,其后也常常添加一些温度的高次幂,本次研究精确到T-3。
Vogel方程形式为
lnv=A+B/(T+C)。
(4)
式中:A,B,C为待确定常数。相较于前述两种黏温方程,Vogel方程适合的温度范围更宽,故应用最广泛。
为了统一形式,可将Andrade方程和Vogel方程中的运动黏度v转换为动力黏度u。动力黏度(简称黏度)可由运动黏度和润滑油密度ρ相乘得到:
u=vρ。
(5)
将式(5)分别代入式(3)和式(4),可以得到动力黏度u关于温度的Vogel形式和Andrade形式方程:
Andrade方程为
lnu=lnρ+A+BT-1+CT-2+DT-3。
(6)
Vogel方程为
lnu=lnρ+A+B/(T+C)。
(7)
润滑油的密度随温度的变化很小,所以一般可认为密度为定值,不随温度发生变化。那么上述两式中的lnρ可看做一个确定常数,lnρ+A部分可作为一个新的待确定常数A′。由此可以认为,润滑油黏度u仍然符合Vogel方程形式和Andrade方程形式。
黏度u与温度T的Andrade方程为
lnu=A′+BT-1+CT-2+DT-3。
(8)
Vogel方程为
lnu=A′+B/(T+C)。
(9)
以润滑油温度T为横坐标、lnu为纵坐标,使用Vogel方程、Andrade方程和Reynolds方程形式对原润滑油进行黏温方程拟合,结果如图3和表1、表2、表3所示。结合上述结果可以看出,Vogel 黏温修正方程与数据最贴近,确定系数R2最接近1,拟合标准差RMSE最小,即Vogel 黏温修正方程拟合效果最好。

图3 15W-40润滑油黏温数据拟合曲线

表1 Vogel黏温方程的拟合参数及其统计分析结果

表2 Andrade黏温方程的拟合参数及其统计分析结果
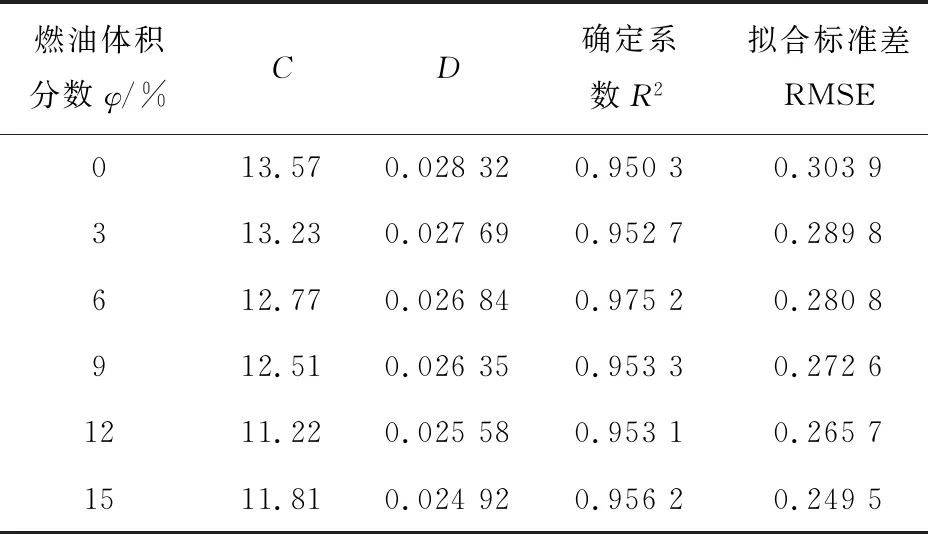
表3 Reynolds黏温方程的拟合参数及其统计分析结果
2.2 燃油体积分数与黏度关系分析
15W-40润滑油燃油稀释后的黏度不仅取决于温度,还取决于燃油体积分数φ。在对稀释后润滑油的黏温关系进行研究时,为了方便与原润滑油黏度进行比较,定义新的变量N,N的意义是同一温度下润滑油稀释后的黏度ua与原始黏度u的比值,即
N=ua/u。
(10)
相同温度下,燃油稀释后润滑油的黏度小于原润滑油黏度,由此可知N值恒小于1。N值越接近于1,说明稀释前后润滑油黏度改变越小,稀释作用对黏度影响越不显著。相反,N值越偏离1,说明稀释前后润滑油黏度改变越大,稀释作用对黏度影响越显著。在不同燃油体积分数下N值随温度的变化曲线见图4。

图4 不同燃油体积分数与温度下的N值
在20~180 ℃温度区间,对φ值为3%,6%,9%,12%,15%的5条N-T曲线进行函数方程拟合,函数选择自定义方程类型,由于N-T曲线趋势类似于对数函数,因此可选用对数函数对N-T曲线进行拟合,拟合方程如下:
N=Aln(T+B)+C。
(11)
式中:A,B,C均为待测常数。
拟合结果如表4所示。由表4可以看出,拟合方程均具有很高的拟合精度,N=Aln(T+B)+C可以用来描述不同φ值下N和温度T(20~180 ℃)的函数关系。

表4 N=Aln(T+B)+C方程的拟合参数和统计结果
3 基于温度和燃油稀释的润滑油黏度神经网络模型研究
考虑到上述黏温方程只能实现特定燃油体积分数下的黏度预测,为了同时覆盖温度和燃油稀释两个参数对黏度的影响,所以采用反向传播神经网络的方法,在20~180 ℃的温度范围,0%~15%的燃油体积分数范围内,实现对任意温度、任意稀释程度下的黏度数值进行预测。
3.1 BP神经网络模型
对润滑油黏度随温度和燃油体积分数变化的数据进行拟合,试验数据可看作闭区间连续函数,因此一层的隐含层足以满足计算需要。输入层和输出层的神经元个数由数据维度确定,对于本次试验,影响润滑油黏度的因素有润滑油温度和燃油体积分数,即有2个自变量,1个因变量。反映到神经网络中,输入层输入二维数据温度和燃油体积分数,包括2个神经元,输出层只输出黏度一维数据,神经元个数只有1个。隐含层神经元个数可根据实际情况选择,这里使用Kolmogorov定理[16],即隐含层神经元个数为
s=2n+1。
(12)
式中:n为输入层神经元个数。本研究中输入层神经元个数为2,则隐含层神经元个数为5。构建好的BP神经网络见图5。

图5 BP神经网络
利用测试数据对BP神经网络进行训练、验证和测试。对15W-40润滑油在燃油体积分数为0%,3%,6%,9%,12%,15%,温度在20~180 ℃之间的黏度进行测量,共得到966个数据点。经过神经网络工具箱自动打乱处理后,可选择70%的数据(676个样本)用于BP神经网络Train(数据训练),15%的数据(145个样本)用于BP神经网络Validation(数据交叉检验),15%的数据(145个样本)用于BP神经网络Test(数据测试)。
选择Levenberg Marquardt训练算法对样本数据进行训练、交叉检验和测试。均方误差越小,说明预测值和设定值越接近;R回归值表示预测值和设定值的关系度,R越接近1,说明预测值和设定值关系越密切。
图6示出BP神经网络训练、验证、测试过程。一般来说,在使用BP神经网络拟合数据时,随着迭代次数的增长,Train数据和Test数据的预测值和设定值的均方误差会越来越小,但Validation数据的均方误差反而会有所提高,为了避免BP神经网络对数据拟合超过限值,本次试验设定当Validation数据的均方误差接连上涨6次后迭代过程结束。本次计算中润滑油黏度数据在迭代第484次表现出最好的训练性,在此停止迭代。

图6 BP神经网络训练、验证、测试过程
图7分别展示了训练集、验证集、测试集、总体的回归分析结果,回归值R均为1,说明预测值和设定值非常接近,BP神经网络拟合效果很好。

图7 BP神经网络回归分析
由于润滑油黏度在不同的温度和燃油体积分数下数值相差较大,预测值与设定值的差值不能很好地表现BP神经网络预测的准确性,于是取差值与设定值的百分比作为误差进行分析。
从图8中可以看出,922个样本预测值与设定值的误差在0%~2%,占90%以上;39个样本的预测值和设定值误差在2%~4%之间,约占4%;仅有5个样本的预测值与设定值之间的误差超过了4%。证明了BP神经网络模型在预测15W-40润滑油黏度方面具有较高的准确性,可以用来预测任意温度和燃油体积分数下的润滑油黏度,以减少不必要的黏度测量,大大减少测量成本。

图8 黏度预测值误差
3.2 基于神经网络的黏度预测
在20~180 ℃的温度范围,0%~15%的燃油体积分数范围内,通过神经网络可以预测任意条件(温度、燃油体积分数为变量)下的润滑油黏度,本研究采用三维曲面图直观显示黏度随温度和燃油体积分数的变化规律。在20~180 ℃温度区间每隔1 ℃取点,在0%~15%燃油体积分数区间每隔0.5%取点,共获得161×31组输入数据,将其输入到已构建完成的润滑油黏度神经网络模型中,可以获得与之对应的161×31组黏度预计值,结果见图9。

图9 黏度随温度和燃油体积分数的变化
从图9中可以很直观地看出15W-40润滑油黏度随温度和燃油体积分数变化的趋势,温度升高、燃油体积分数增大均会造成15W-40润滑油黏度下降,相较于燃油体积分数,温度对15W-40润滑油黏度的影响更明显,并且随着温度的升高,燃油体积分数对黏度的影响逐渐减弱。
4 结束语
以15W-40润滑油为研究对象,构建了燃油体积分数为3%,6%,9%,12%,15%下的Vogel,Andrade和Reynolds黏温方程,通过比较发现Vogel 黏温修正方程拟合效果最好。构建了稀释黏度比-温度方程,以此反映在不同温度下燃油稀释后黏度相对于原润滑油的变化程度。构建了考虑温度和燃油稀释的 BP神经网络黏度模型,适用温度范围为20~180 ℃,燃油体积分数范围为0%~15%,实现了同时以润滑油温度和燃油体积分数为参数的润滑油黏度准确预测。以15W-40润滑油为对象进行了黏度预测,结果显示90%的预测值与设定值的误差小于2%,整体数据误差不超过6%。

