在线黏度测量过程中黏温补偿计算方法的误差研究
丁晓炯
(笙威工程技术服务(上海)有限公司, 上海 201399)
0 前言
黏度测量是很多行业生产或应用中十分重要的指标。不同聚合物随着相对分子质量的变化,黏度相应呈现出不同变化规律,大致都是随着相对分子质量的增加,黏度也相应增加,这也是很多在聚合过程监控和浓度(含量)等控制中采用黏度作为测量手段和表征方法的原因,因此,许多过程中都需要进行黏度的连续自动测量与控制[1-2]。
在涂料生产和涂装过程聚合反应及使用高分子材料过程中,涉及到黏度测量和控制的情况有很多:各种聚合物或含聚合物的各类液体;单体到后续的产品;各种树脂聚合物液体和不同浓度及比例的液体等,都有监测黏度的需要。当进行各种涂装过程在使用高分子材料时,往往需要先进行物料的黏度测量和控制,物料黏度的不稳定或流变特性的问题会影响完成该过程之后的产品质量,如涂层的厚薄、均匀性、收缩性、色彩的一致和均匀性、黏合性等,甚至影响产品的最终质量。因此很多行业已经开始应用在线黏度测量技术,国内也已经有不少企业尝试和比较成熟地使用该项技术。但是由于物料本身的流变特性、在线测量时实时条件的变化(温度、搅拌、流动等因素)、实验室测量结果对比条件的不同,导致了有些企业感觉在线黏度测量技术不成熟、不好用。这主要是由于对物料流变特性的不了解、黏度测量技术的不理解以及没有掌握测量条件变化对黏度测量值影响关系而造成的,这些问题都可以从流变理论和仪器测量原理的角度来进行分析和解决[3-4]。
1 黏度测量的影响因素
在黏度测量过程中,除去测量方法和物料自身结构、相对分子质量、挥发等因素外,其他主要的影响因素有:温度、压力、剪切率(流场、管道、测量方法和测量条件等),本文讨论温度对黏度的影响。
流体的黏度会随温度的波动而变化,现场的温度往往是会波动的。实验室一般是在恒温下进行测量,该温度经常和现场温度不一样,因此需要根据实测的数据进行流体黏度和温度关系的计算,这样才可以得到指定温度下的在线黏度值,得到的数据才可以在同一标准下进行比较。其间的黏度和温度关系取决于流体的黏温特性,不同流体的参数是不同的,不一定是一个简单的线性关系。
姜继海等[5-6]对于物料的黏温特性研究提出了一些模型和计算方法,这些方程都是针对那些特定研究物料做出的归纳总结,作为研究某些特定物料的黏温特性研究可以提供参考和指导。
实际的在线黏度测量过程中,客户往往会希望通过实测的温度和黏度值,通过黏温补偿计算得到一个指定温度下的黏度值,而这个指定温度往往就是在实验室采样测量的温度。本文通过对实际使用过程的分析,专门设计了相应的算法来进行黏温补偿计算[7],并对不同算法进行误差分析。
2 黏温补偿计算过程
2.1 黏温曲线分类及计算
通过之前的介绍可知,物料的黏温曲线会有所不同。根据实测的经验,黏温曲线关系如下:
(1) 当温度范围不大时,黏温曲线接近于线性关系,见图1;
(2) 当温度范围较大时,黏温曲线是非线性关系,见图2。
从图1可以看出:当温度范围较小时,黏温曲线更接近于线性关系,可以利用Excel收集在线测量的结果,然后做相应的回归计算,判断是否是线性关系;当温度范围较大时,黏温曲线更接近于非线性关系,可以利用Excel收集在线测量的结果,然后做相应的回归计算,判断是否是非线性关系,在实际中大多采用幂函数方程进行黏温补偿计算。

图1 黏温曲线及关系曲线
2.2 黏温补偿计算误差计算
采用数值模拟的方法进行黏温补偿计算的误差分析。假设一种物料的黏温特性在温度5~150 ℃变化,黏温特性关系符合非线性变化规律,η=2 000×T-0.5,根据最先二乘法得到线性补偿的黏温特性曲线就是η=-2.904 1×T+510.84,然后按线性补偿方法和非线性补偿方法进行计算,补偿计算到指定中间温度75 ℃的黏度,对结果误差进行计算和统计计算。为计算方便,假设在线黏度测量本身没有误差,只研究两种不同补偿计算方法间的计算差异。
根据计算,可以得到不同温度T、黏度η、线性补偿计算得到的黏度、非线性补偿计算得到的黏度、两种结果的绝对误差、相对偏差线性补偿,如表1所示。
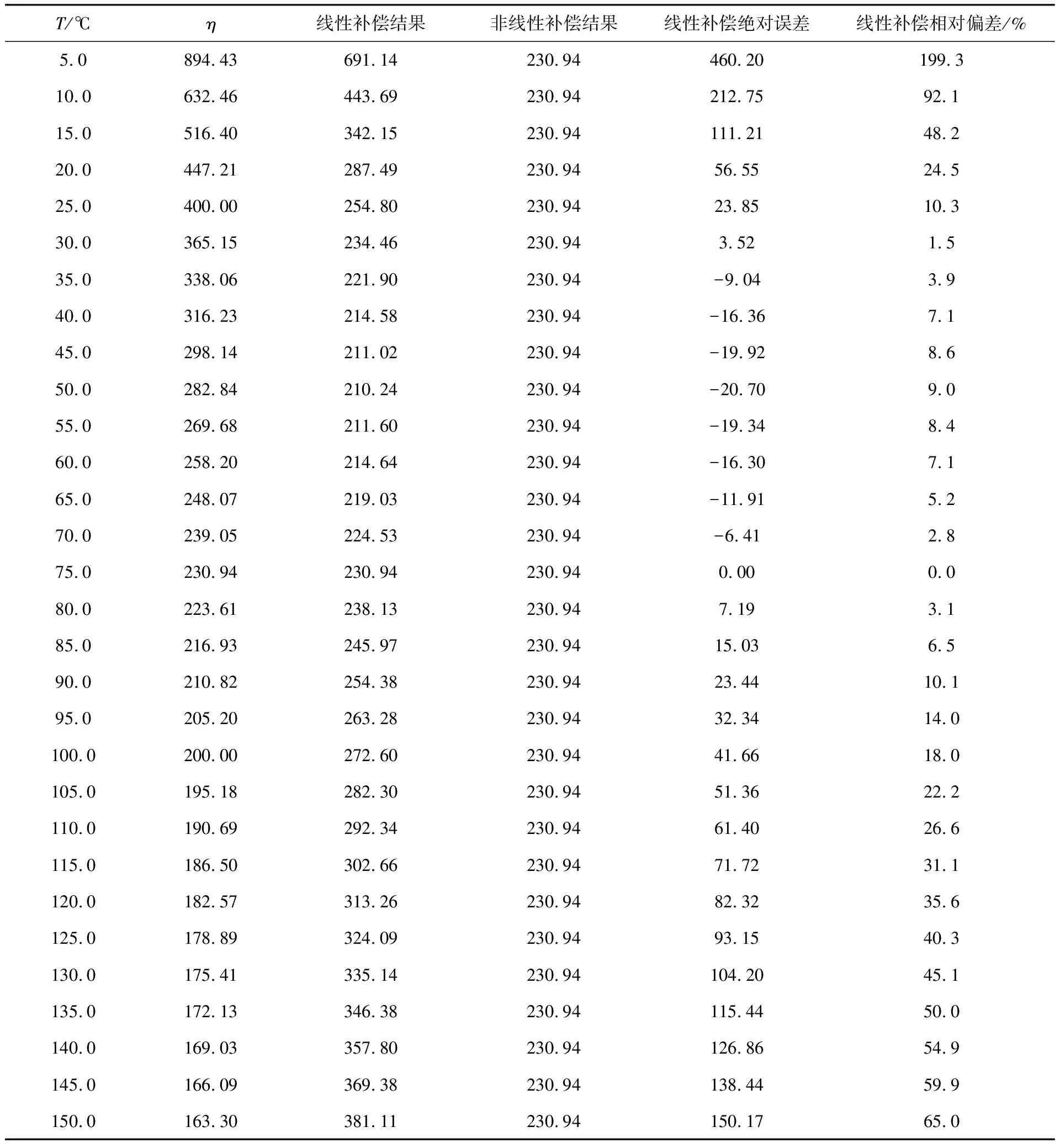
表1 线性补偿、非线性补偿计算结果和误差结果
根据计算结果,利用Excel对以上结果进行画图以直观表示,见图2。从表1和图2可以得到以下结果:
(2)内部物流体系低能高耗、漏洞百出。鄂州市大中型工商企业几乎80%都拥有自营的物流公司,但总体运营情况都不好,既抵减了物流市场的活力与动力,又扩大了自身的物流成本和资产秏费,有的管理混乱漏洞百出。比如在鄂城某钢厂,“靠车吃饭”“靠船吃饭”“靠中介吃饭”等,常常发生“面上干工作、底下揽私活”的行为,这些“吃里扒外”的人和事,致使出现了物流越忙、亏损越多的尴尬境地。同时,第三方物流体系杂乱、层级与结构不配匹,物流业态呈畸形生态。
(1) 非线性补偿计算的结果和标准值在任一温度点都没有任何偏差,补偿计算结果完全符合设定黏温特性;
(2) 线性补偿计算的结果在不同的温度段呈现不同的误差,正、负误差都有,整体呈现两大段,即小于计算温度点一段(正、负误差都有)和大于计算温度点一段(正误差),计算温度点(75 ℃)误差最小;
(3) 线性补偿计算的相对偏差最大可以达到199.3%,平均相对偏差为21.4%;
(4) 线性补偿计算时,计算点越靠近指定点75 ℃(即温度波动范围越小),绝对偏差和相对误差也越小,即温度控制得越好,计算误差也越小,结果越准确。

图2 黏温曲线和补偿计算结果误差
3 结论
经过以上的介绍可以看到,在线黏度测量中,温度对黏度的影响是很大的,对于一些没有进行温度控制、控制得不够稳定或者需要知道指定温度下黏度值的场合而言,就需要运用黏温补偿的方法来进行计算,而计算的准确性取决于所选取的计算方法。
(1) 如果温度波动范围小或者在线温度和指定计算温度差异小,可以采用线性补偿计算方法。但此范围大小取决于物料的黏温特性(一般不超过30~50 ℃),不能照搬。
(2) 如果温度波动范围大或者在线温度和指定计算温度差异大,一定要采用非线性补偿计算方法。非线性方法在较宽的温度范围内几乎适用绝大多数场合,线性关系也可以用非线性关系来代替,计算误差很小(平均相对偏差小于5%),见图3,线性补偿有一定的局限性,不同温度段的误差情况也有不同。
(3) 物料的黏温关系曲线是需实测数据的,不能根据别的物料曲线照搬。

图3线性补偿计算在不同温度段的情况
黏温补偿计算是在线黏度测量中很重一个步骤,需要根据物料的黏温特性和计算要求进行方法的选择和计算,对于特定的行业和产品,这些方法和参数可以借鉴,但不建议照搬,可以逐步积累数据,建立起自己产品的数据参数库,这些参数是自己产品的生产工艺参数和技术诀窍(know how)。我公司根据以上的分析,设计了相应的显示控制器,接入在线温度、黏度信号,可以自行输入参数,选择线性或非线性补偿计算方式,实现在线实时、自动完成黏温补偿计算并自动存储数据。

