一类半参尾指数估计量的渐近性质①

余乐乐， 彭作祥

西南大学 数学与统计学院，重庆 400715

设{Xn,n≥1}为独立同分布的随机变量序列, 其分布函数为F(x)．X1,n≤…≤Xn,n表示X1,…,Xn的次序统计量． 若存在规范化常数an>0和bn及非退化分布函数Gγ(x)使得

(1)

由文献[1-2]可知

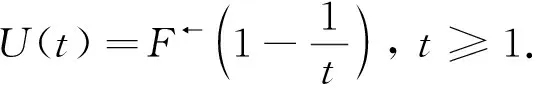
(2)

文献[3]提出了著名的Hill估计量． 文献[4]为减小Hill估计量的偏差, 构造了矩率估计量． 文献[5]利用函数gr,u(x)=xrlnu(x),x≥1构造出如下的统计量

(3)

其中γr<1,u>-1． 利用(3)式可以将Hill估计量、 矩率估计量表示出来:

极值指数估计的应用非常广泛, 相关研究可参见文献[6-10]．

本文利用统计量Gn(k,r,u)构造如下的尾指数估计量

(4)

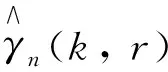
(5)

1 相合性和渐近正态性

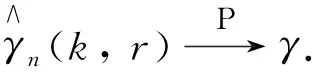
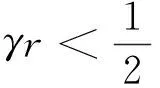
(6)

其中

2 定理的证明

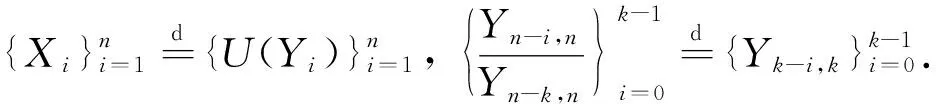
得到

利用连续映射定理[12]和Slutsky定理[13], 定理得证．

对定理2的证明, 我们需要下面的辅助引理．

(7)

其中

(N1,N2)是二维零均值高斯向量, 满足

其中

证由二阶正规变换条件(5)式知, 对充分大的t,

则

(8)

(9)

利用文献[14]中的Cramer-Wold定理证明(7)式成立． 对任意(φ,ψ)∈R2, 有

(10)

其中

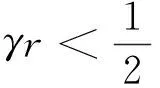
由列为林德伯格中心极限定理可得

(11)

与文献[15]引理1类似计算, 有

(12)

由(11)式,(12)式及Slutsky定理, 知

(13)

结合(10)式和(13)式, 引理得证．

定理2的证明定义

利用泰勒展式, (8)式和(9)式化简为

得到

即

由引理1知

结合(6)式, 定理2得证．