结合桥梁实际影响线信息的预应力识别方法
王宁波 王灿 沈伟 黄天立


摘要: 预应力技术广泛应用于桥梁工程领域,对于在役桥梁结构,随着服役时间延长不可避免地存在预应力损失。准确识别桥梁预应力有助于了解其实际承载能力,保证桥梁长期安全稳定运营。本文研究预应力导致影响线的变化机理,建立预应力与桥梁影响线之间的对应关系(预应力梁影响线微分方程),并给出解析与数值求解方法,通过与仿真计算结果比较验证微分方程的正确性。研究预应力筋线形对挠度影响线(Deflection Influence Line,简写为DIL)的影响,在此基础上将影响线微分方程进行简化,提出结合实际影响线的预应力识别方法。开展预应力梁桥车?桥耦合数值仿真试验,进行桥梁动力响应计算和影响线提取,验证本文结合桥梁实际影响线进行预应力识别方法的正确性与可行性。
关键词: 预应力识别;桥梁影响线;移动荷载;影响线微分方程;基函数
中图分类号: U441;U448.35 文献标志码: A 文章编号: 1004-4523(2023)03-0688-10
DOI:10.16385/j.cnki.issn.1004-4523.2023.03.011
引 言
预应力可改善桥梁结构的受力状态,使其具有跨度大、自重小、经济实用等优点[1],已广泛应用于桥梁工程领域。在桥梁服役期间,由于混凝土徐变、预应力筋松弛等诸多因素,不可避免地发生预应力损失,从而出现梁体底面开裂、桥梁线形变化、结构响应增大等现象,导致桥梁结构承载能力下降、使用寿命缩短,严重时造成灾难性事故[2]。当前中国桥梁事业发展方向已从大举建设转向结构长期安全稳定运营,如何快速、经济、准确地评估、识别在役桥梁结构实际预应力状态具有重要意义。
针对预应力的直接测试方法(如:超声波[3]、应力释放法[4]、预埋传感器法[5]和反拉法[6]等)虽能实现对预应力的有效检测,但往往需要在桥梁建设初期预先布置传感器,随着时间延长这些测试元件不可避免发生损坏,并且还存在造成结构损伤、适用性有限等不足;其他外在因素也会对测试结果造成干扰,这种直接以预应力筋为测试对象的方法离实际应用推广仍存在距离。
结合桥梁当前状态下的特征参数或荷载效应进行预应力识别是研究的热点,多以模态、振型为特征参数进行研究。张耀庭等[7]通过自振频率的变化识别桥梁预应力,其研究指出一阶以上的频率误差较大,无法与预应力建立对应关系。刘龄嘉等[8]基于实测频率回归出的预应力与有效刚度的函数式进行预应力识别。刘承斌等[9]通过研究桥梁预应力与自振频率的关系,提出结合神经网络识别预应力损失的方法,该方法需要大量的试验测试,且通常适用于模型试验梁体 ,对实际桥梁不具有普遍性 。Law等[10]基于模态叠加法研究预应力梁动力响应,将预应力和抗弯刚度作为识别动力响应的未知量,提出识别预应力的反演问题。总体而言,通过模态参数对预应力进行识别的成功案例较少,多数研究表明频率对预应力的敏感度较小且变化趋势不明,这类方法对测量数据和计算模型的精度有较高要求,且不易建立明确的对应关系[11?13]。
基于桥梁荷载效应进行预应力识别研究近年来也颇受关注。一般而言包含两个方面,其一是通过比较预应力直接作用下的桥梁荷载效应进行识别。刘艳辉等[14]基于影响矩阵原理,建立预应力损失值与桁架结构测点位移值的对应关系。刘寒冰等[15]通过对预应力荷载作用下跨中挠度和应变数据长期监测,提出以挠度?应变比值(f/ε)为参数的预应力损失计算方法。直接以预应力荷载作用下的桥梁响应作为研究对象进行预应力识别,虽有较明确的对应关系,但通常需要长期试验测试,以历史数据为基准进行识别分析,导致其经济性欠缺,且长期测试过程中不确定因素较多。
基于荷载效应进行预应力识别的另一思路则是以外荷载(如:车辆荷载)作用下的荷载效应为研究对象,进行预应力间接识别,这类方法不需要长期或持续的数据监测。Zhang 等[16]基于位移反演方法,根据车辆通过桥梁时的实测位移数据识别预应力。Lu 等[17]结合桥梁动力响应,将预应力作为正弦脉冲激励的未知参数进行预应力识别研究。卜建清等[18]提出基于车激动力响应的 BP 神经网络方法识别有效预应力,通过数值模拟动力响应识别简支梁桥有效预应力。Hai 等[19]通过车辆过桥数值模拟,建立预应力与桥梁动力响应之间的关系。事实上,外荷载下桥梁响应与预应力不存在直接对应关系,并不是敏感因子,使得离散测点信息无法直接描述复杂结构的预应力实际状态。并且车辆激励下的桥梁响应一般包含测试噪声、桥梁振动等干扰信息,不利于预应力识别。
近年来,针对桥梁实际影响线的提取及应用是广泛关注的热点。桥梁影响线一般从确定性移动荷载的桥梁响应信息中提取,它是反映结构固有特征的静力参数,相比模态参数具有较好的完整性和准确性,而且提取过程中去除了原始響应信息存在的噪声及振动干扰。其数据信息丰富,广泛用于桥梁损伤识别[20]、模型修正[21]、承载能力快速评估[22] 等问题的研究,被认为是桥梁评估颇具潜力的指标之一。
本文开展基于桥梁实际影响线信息的预应力识别研究,以桥梁实际影响线提取的前期研究为基础,研究预应力导致影响线的变化机理,建立预应力?影响线之间的对应关系(影响线微分方程),求解并验证其正确性;研究预应力筋线形对 DIL 的影响,对影响线微分方程进行简化描述,在此基础上提出结合桥梁实际影响线的预应力识别方法。开展预应力梁桥车?桥耦合数值仿真试验,进行桥梁动力响应计算和影响线提取,验证本文结合影响线进行预应力识别方法的正确性与可行性。
1 预应力对 DIL 的影响机理
以简支梁为例研究预应力对 DIL 的影响,对同等无预应力桥梁而言,预应力的存在使得在同样载荷作用下梁的荷载效应变小,影响线作为桥梁归一化的荷载效应,也会相应变小。假定无预应力状态下桥梁挠度影响线为 DIL0,由预应力所引起的变量为 ΔDIL,预应力梁的实际影响线记作 DIL,则三者满足 DIL = DIL0-ΔDIL。
1. 1 预应力梁影响线微分方程
预应力梁可视为梁和筋的组合结构,预应力对梁体作用可等效为竖向外荷载 q(x)[23],其取值与预应力筋线形、轴向力大小相关。将第 i 根预应力筋的等效荷载记为 q(i x),如下式所示:式中 y(i x)表示第 i 根预应力筋线形函数;Npi表示其轴向力;C(i x)为预应力筋切向角的余弦值。
在外荷载作用下,预应力筋线形随梁体改变,线形变化导致其等效竖向荷载产生一定增量,如图 1所示。
图 1 中:Lb 为梁长,lp 为单位力距端部的距离。由于各预应力筋与梁体共同变形,Δy(i x)为加载前后 预 应 力 筋 线 形 改 变 量 ,均 等 同 于 梁 的 挠 曲 线ω(x)。则第 i 根预应力筋因梁变形量导致的等效荷载增量 Δq(i x)与 ω(x)和 Npi相关,具体如下式所示:
橋梁实际抗弯刚度为 EI(x)=λ(x)EI,其中 :λ(x)表示桥梁截面沿桥长方向的变化函数,可根据桥梁几何参数得到,EI 为未知常量。单位力作用下挠曲线 ω(x)即为挠度影响线 DIL,则 DIL 与预应力之间满足以下关系(预应力梁影响线微分方程):
预应力梁 DIL 与预应力值之间存在对应关系,且与实际抗弯刚度、预应力筋线形有关。在桥梁各参数已知情况下,通过该微分方程可求得预应力梁DIL。
1. 2 方程求解及验证
对于梁体为均刚度,预应力筋为直线形的特定情况,几何参数 C(i x)和 λ(x)恒为 1,式(8)可简化为二元常系数非齐次线性微分方程:
引入简支梁边界条件及测点处连续、可导条件可求出系数 C1~C4,从而得到预应力简支梁在特定情况下的解析解。
对于变刚度、多根预应力筋及预应力筋线形非直线等一般情况,则无法求得解析解。尽管如此,在桥梁几何、物理参数及预应力筋形式、预应力大小确定的情况下,桥梁实际影响线具有唯一性。基于此,本文提出针对一般情况下预应力梁的影响线微分方程数值迭代求解方法,具体如下:
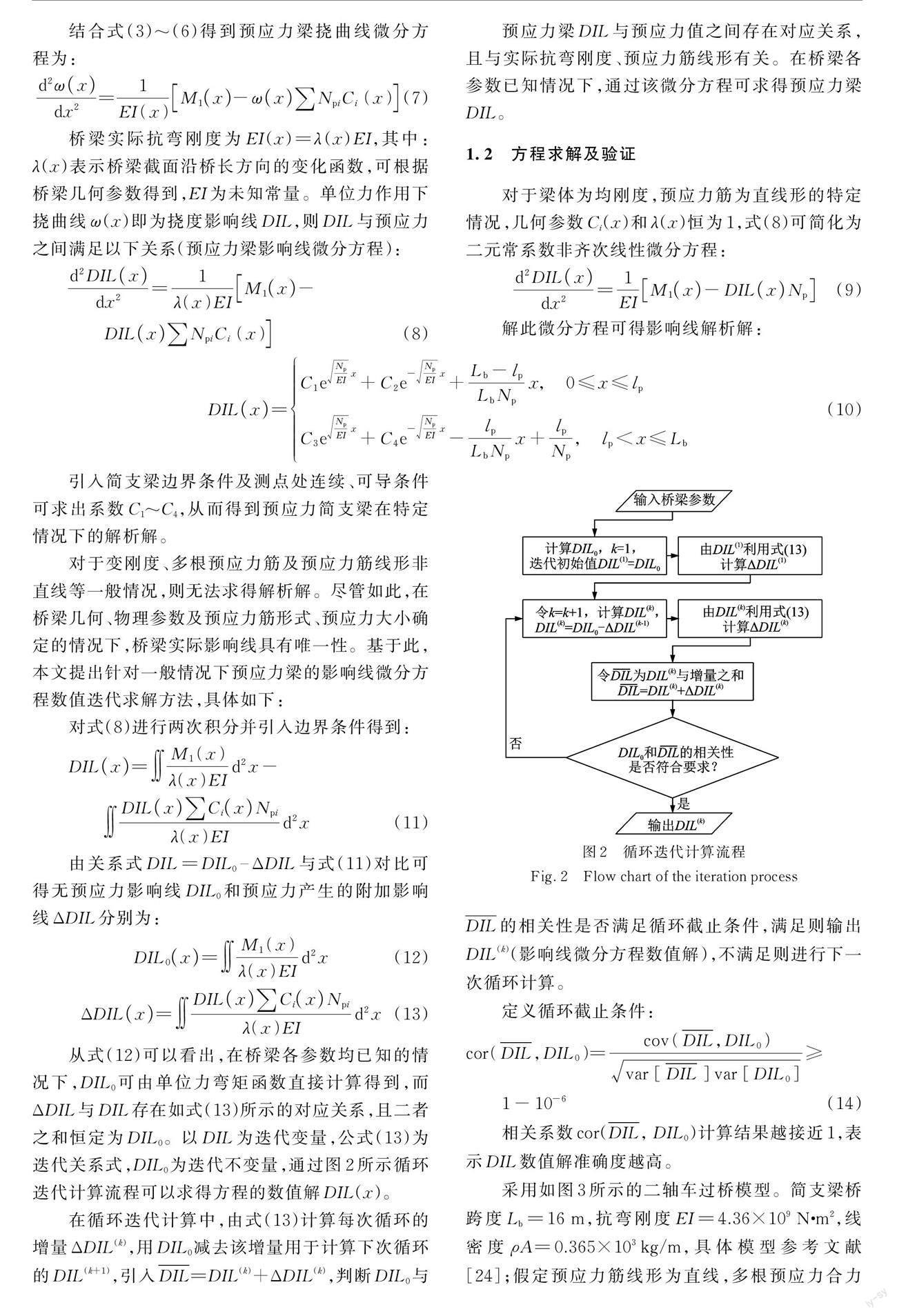
从式(12)可以看出,在桥梁各参数均已知的情况下,DIL0可由单位力弯矩函数直接计算得到,而ΔDIL 与 DIL 存在如式(13)所示的对应关系,且二者之和恒定为 DIL0。以 DIL 为迭代变量,公式(13)为迭代关系式,DIL0为迭代不变量,通过图 2 所示循环迭代计算流程可以求得方程的数值解 DIL(x)。
在循环迭代计算中,由式(13)计算每次循环的增量 ΔDIL(k),用 DIL0减去该增量用于计算下次循环的 DIL(k+1),引入 -DIL=DIL(k)+ΔDIL(k),判断 DIL0与DIL 的相关性是否满足循环截止条件,满足则输出DIL(k)(影响线微分方程数值解),不满足则进行下一次循环计算。
定义循环截止条件:
采用如图 3 所示的二轴车过桥模型。简支梁桥跨度 Lb = 16 m,抗弯刚度 EI = 4.36×109 N·m2,线密 度 ρA= 0.365×103 kg/m,具 体 模 型 参 考 文 献[24];假定预应力筋线形为直线,多根预应力合力为 2.5×104 kN。二轴车车体质量 m1=17735 kg;车轴及车胎刚度、阻尼等特性参数源于文献[25]。
根据桥梁位移响应提取实际 DIL[25];由式(10)计算 DIL 解析解;通过循环迭代计算得到 DIL 数值解,三者比较如图 4 所示。对比 DIL 解析解、DIL 数值解和实际 DIL,三者具有较好的一致性,表明本文微分方程解析解和循环迭代数值求解方法的正确性。
1. 3 预应力筋线形影响
包含线形信息的 C(i x)是影响 DIL 的潜在因素,结合数值模型研究预应力筋线形对 DIL 的影响。以直线、曲线和折线三种线形为例,其中曲线预应力为二次函数布置,折线预应力筋为分段函数布置,分别如图 5(a),(b)所示。
桥梁参数选用图 3 模型参数计算,其他模型参数还包括梁高为 1.2 m,l1=1.5 m,l2=14.5 m,eA=eB=0.3 m,f=0.6 m。对于 3 种线形,预应力大小均为 2.5×104 kN。根据循环迭代计算,求得不同预应力筋线形下的 DIL,如图 6 所示。
可以看出,3 种不同预应力筋线形导致的 DIL几乎重合,因此对于桥这种梁式结构,可将预应力筋线形视为直线,忽略局部弯曲的影响。即取不同预应力筋线形余弦函数 C(i x)= 1,有:
预应力对梁的作用表现出整体性,预应力合力是预应力状态的决定性参数。每根预应力筋实际保有值对梁体的影响均会在合力中表现,即预应力识别重在识别其预应力合力 Nd。
2 基于函数拟合的预应力识别方法
对于实际情况而言,DIL 可根据移动荷载试验得到,λ(x)和 M1 可直接根据桥梁几何参数计算得到。根据公式(16),利用已知 DIL,M1及桥梁几何参数构建基函数,提出结合基函数进行桥梁预应力识别的方法。
2. 1 基函数构建
基函数 ζ0 可通过桥梁几何参数及测点位置计算得到;基函数 ζ1 可通过预应力梁实际 DIL 及桥梁几何参数计算得到。
令式(17)中常量为 β0与 β1:
图 7 中 β0ζ0即为单位力作用下的影响线;预应力影响下 DIL 的变化为 β1ζ1,其与预应力合力 Nd存在着明确的对应关系,实际影响线即为两者之和。
2. 2 预应力识别方法
将构建的基函数代入式(17),可得到预应力梁实际影响线与基函数 ζ0 与 ζ1 之间的关系式:
假 定 基 函 数 ζ0 与 ζ1 和 DIL 离 散 ,则 可 将 上 式记为:
对上式进行矩阵求解可得 β0与 β1,联合式(19)可求得预应力合力 Nd:
需要注意的是,由于预应力产生的附加挠曲线和荷载产生的挠曲线在形式上较为一致,难以分离,表现为两个基函数 ζ0 与 ζ1形状一致,其形成的矩阵存在一定的病态性,造成求解误差。可选取合适测点以增加基函数的差异,达到增加精度的目的。
本文基于 DIL 拟合基函数识别预应力的方法可对一般形式的简支梁桥进行识别,其仅需桥梁的基本几何参数(桥长、截面形状和测点位置)和 DIL 等信息。识别结果为桥梁预应力合力值,可对桥梁承载能力评估、体外预应力加固和提高桥梁荷载等级提供指导 。基于DIL预应力识别方法具体思路如下:
步骤一:开展移动荷载试验,并采集桥梁测点位移响应信息;
步骤二:通过桥梁测点位移响应提取准静态、高精度的 DIL;
步骤三;根据单位力作用下的弯矩函数 M(1 x)及橋梁参数 λ(x)构建基函数 ζ0 ,提取 DIL 及桥梁参数 λ(x)构建基函数 ζ1 ;
步骤四:根据基函数 ζ0 与 ζ1 通过式(21)求解得到系数 β0 与 β1,并利用式(22)求得 Nd。
3 数值试验研究
3. 1 预应力桥梁车?桥耦合模型
采用二轴车移动模型,将车体简化为多自由度系统(多刚体系统)。桥梁及车辆模型与第 1 节算例相同,模型计算示意图如图 8 所示。
将预应力加入桥梁振动方程中,并综合考虑偏心预应力、预应力筋与管道间摩擦等,建立预应力桥梁的竖向振动方程。通过参考文献[26?27]建立预应力梁竖向振动方程:式中 M,C 和 K 分别为预应力梁的质量矩阵、阻尼矩阵和刚度矩阵,F 代表车轴激励力的向量。对于偏心预应力梁而言,其刚度矩阵可描述为:式中 K 为梁体实际刚度矩阵;K0,KN,KM分别为无预应力梁刚度矩阵、轴向预应力引起的刚度矩阵和预应力偏心弯矩引起的刚度矩阵;ki0,kiN,kiM分别为单元的弹性刚度矩阵、轴向预应力引起的单元刚度矩阵和预应力偏心弯矩引起的单元刚度矩阵。
根据文献[26]可知,轴向预应力引起的单元刚度矩阵 kiN可通过下式求得:
根据文献[27]可知,预应力偏心弯矩引起的单元刚度矩阵 kiM 可描述如下:
式中 A 为预应力钢筋截面积,S'为样条曲线形函数矩阵,M(x)为偏心预应力所产生的偏心弯矩,wM为偏心弯矩所导致的挠度,此处考虑摩擦损失,计算时已将预应力值进行折减。
3. 2 测点位移响应分析与 DIL 提取
车?桥时变系统运动方程充分考虑了车辆、桥梁的各个竖向自由度,是复杂的动力系统。采用 Wil?son?θ 逐步积分法求解移动车辆作用下桥梁不同截面的时程测点位移响应。
以行车速度 v =5 m/s、路面不平度等级为 C 作为计算条件,并对计算结果附加 10% 的高斯白噪声模拟测试噪声,以表 1 中工况计算车过桥各测点的位移响应曲线如图 9 所示。
从图 9 可以看出,测点位移响应随预应力减小呈现增加趋势,但由于测试噪声、桥梁振动等因素的影响产生了较多波动干扰信息,导致不同预应力下的位移响应相互交错难以区分,辨识度差。
根据影响线理论特征,利用三次多项式分段函数拟合上述响应,计算得到桥梁实际影响线。通过交替改变多段函数的分段模式逐步消除波动干扰,得到高精度、准静态的 DIL[25],各工况下计算提取的DIL 曲线如图 10 所示。
从图 10 可以看出,由多段函数拟合计算提取的影响线具有准静态特性,较好地去除了实际响应中包含的波动干扰信息。且随着预应力减小,计算得到的 DIL 呈现增加趋势,两者有明显的对应关系,不同工况下影响线幅值变化如图 11 所示。
根据数据计算结果 ,比较不同预应力工况下DIL 幅值与无预应力情况下的相对变化量,具体如表 2 所示。
对比在各工况下不同位置的 DIL 幅值,其幅值与预应力均存在明显对应关系。本算例中预应力导致的桥梁各测点 DIL 最大变化量约为 12.7%,需要指出的是预应力对荷载效应的影响还与桥梁结构形式、预应力大小等因素密切相关。
3. 3 预应力识别
通过测点位移响应提取的实际影响线,根据第2 节拟合基函数进行预应力识别。各工况下系数 β0与 β1的计算结果及预应力的识别结果如表 3 所示。
由表 3 中数据可以看出,针对预应力系数 η 分别取值 1.0,0.8,0.6,0.4,0.2 的 5 种工况,本文基于基函数拟合计算识别的预应力值与车辆过桥仿真计算时采用的输入值具有较好一致性,其相对误差均在 5% 以内。表明了本文结合桥梁实际影响线进行预应力识别方法的正确性与可行性。相较而言,绝对预应力值越大,由于其导致的荷载效应变化越明显而更利于准确识别。对比各工况下识别结果相对误差可发现,基于 1/2Lb处测点数据的预应力识别结果较 1/8Lb和 1/4Lb处误差更大。分析可知,识别误差主要在求解由基函数所构成矩阵的广义逆矩阵时产生,两基函数差异越大,则预应力识别误差越小。
以 η=0.8 为例,分别求出 1/2Lb 和 1/4Lb 测点处对应基函数 ,将其归一化处理并进行对比 ,如图 12所示。
可以看出,测点在 1/2Lb处时,两基函数在形状上比较接近,导致广义逆矩阵求解的精度较差。而当测点在 1/4Lb时,基函数在形状上表现出明显差异,大幅降低了计算误差。不同测点位置两基函数的差异性不同,通过合适的测点选取可保证预应力的识别精度。
4 结 论
本文在准确提取桥梁 DIL 的基础上,通过研究预应力导致影响线的变化机理,建立预应力梁影响线微分方程,对该方程求解、验证并进行简化描述;在此基础上构建针对 DIL 的基函数描述模式,提出一种结合桥梁实际影响线进行预应力识别的基函数拟合方法。开展车辆过桥数值仿真计算,并进行方法验证,得到结论如下:
(1)桥梁实际影响线信息可避免响应信号中包含的测试噪声、桥梁振动等干扰信息;且数据信息量丰富,与绝对预应力值存在明确对应关系,是用于预应力识别的理想参数。
(2)梁式结构中不同线形的纵向预应力筋对DIL 的影响与直线形预应力基本等效,因此可对实际桥梁纵向预应力进行整体描述,将预应力以合力的形式进行识别。
(3)数值计算分析表明本文结合桥梁实际影响线信息的预应力识别方法具有较高精度;对于简支梁桥,当测点位置不在跨中时,基函数的差异性明显,更有利于减小预应力识别误差。
(4)本文预应力识别方法仅以移动荷载试验下桥梁实际影响线提取为前提,进行绝对预应力识别,不需历史数据或基准信息作为参考,具有较高的实用价值。
参考文献:
[1] 吕志涛,刘钊,孟少平 . 浅论我国预应力混凝土梁桥的技术与发展[J]. 桥梁建设,2001(1):52-56.Lü Z T, Liu Z, Meng S P. A brief review on the tech?nology and development of prestressed concrete beam bridges in China[J]. Bridge Construction,2001(1):52-56.
[2] 戴竞,凤懋润 . 我国预应力混凝土公路桥的发展与现状[J]. 土木工程学报,1997(3):3-10.
Dai J, Feng M R. Development and state of art of pre?stressed concrete highway bridges in China[J]. China Civil Engineering Journal,1997(3):3-10.
[3] Bartoli I, Salamone S, Phillips R, et al. Use of inter?wire ultrasonic leakage to quantify loss of prestress in multiwire tendons[J]. Journal of Engineering Mechan?ics,2011,137(5):324-333.
[4] 赵煜,贺栓海 .基于应力释放法的在役组合钢桥承载力评定[J]. 长安大学学报(自然科学版),2006,26(5):40-42.
Zhao Y, He S H. Evaluation for existing truss-cable composite continuous steel bridge based on stress re?lease method[J]. Journal of Chang'an University(Natu?ral Science Edition),2006,26(5):40-42.
[5] 劳晓春,汤立群,任鹏,等 . 桥梁内部预应力钢绞线应变的长久监测与分析[J]. 华南理工大学学报(自然科学版),2003,31(11):53-56.
Lao X C, Tang L Q, Ren P, et al. Long monitoring and analysis on the strain of prestressed twist steel ca?bles inside a bridge[J]. Journal of South China Universi?ty of Technology(Natural Science Edition),2003,31(11):53-56.
[6] 付丹,郭紅仙,程晓辉,等 . 预应力锚索工作应力的检测方法——拉脱法的检测机制和试验研究[J]. 岩土力学,2012,33(8):2247-2252.
Fu D, Guo H X, Cheng X H, et al. Working stress measurement of prestressed anchor cables: detection mechanism and experimental study of lift-off test[J].Rock and Soil Mechanics,2012,33(8):2247-2252.
[7] 张耀庭,汪霞利,李瑞鸽 . 全预应力梁振动频率的理论 分 析 与 试 验 研 究[J]. 工 程 力 学 ,2007,24(8):116-120.
Zhang Y T, Wang X L, Li R G. Experimental and the?oretical research on vibration frequency of full-pre?stressed concrete beam[J]. Engineering Mechanics,2007,24(8):116-120.
[8] 刘龄嘉,贺拴海,赵小星 . 在役混凝土简支梁有效预应力计算[J]. 交通运输工程学报,2005,5(3):47-51.
Liu L J, He S H, Zhao X X. Effective prestress compu?tation of existing PC simply-supported beam[J]. Jour?nal of Traffic and Transportation Engineering,2005,5(3):47-51.
[9] 刘承斌,王柏生,曲昌春 . 用振动法进行 PRC 梁的预应力损失检测[J]. 振动与冲击,2003,22(3):97-99.
Liu C B, Wang B S, Qu C C. Response of guided mis?sile body to vibration of main engine rotor[J]. Journal of Vibration and Shock,2003,22(3):97-99.
[10] Law S S, Zhu X Q. Time domain responses of a pre?stressed beam and prestress identification[J]. Journal of Sound and Vibration,2005,288:1011-1025.
[11] Miyamoto A, Tei K, Nakamura H, et al. Behavior of prestressed beam strengthened with external tendons[J]. Journal of Structural Engineering,2000,126(9):1033-1044.
[12] Saiidi M, Douglas B, Feng S. Prestress force effect on vibration frequency of concrete bridges[J]. Journal of Structural Engineering,2015,120(7):2233-2241.
[13] Xiang Z, Chan T H T, Thambiratnam D P, et al. Pre?stress and excitation force identification in a prestressed concrete box-girder bridge[J]. Computers & Concrete,2017,20(5):617-625.
[14] 刘艳辉,张阳阳,刘军校,等 . 基于影响矩阵的桁架结构 预 应 力 损 失 识 别 方 法[J]. 西 南 交 通 大 学 学 报 ,2019,54(5):1030-1037.
Liu Y H, Zhang Y Y, Liu J X, et al. Prestress loss identification method based on influence matrix in truss structure[J]. Journal of Southwest Jiaotong University,2019,54(5):1030-1037.
[15] 劉寒冰,罗国宝,吴春利 . 简支桥梁预应力损失计算方法[J]. 哈尔滨工程大学学报,2016,37(11):1510-1513.
Liu H B, Luo G B, Wu C L. Calculation method for the prestress loss of a simply-supported bridge[J]. Jour?nal of Harbin Engineering University,2016,37(11):1510-1513.
[16] 张兆宁,贺拴海,赵煜 . 基于反演理论在役连续刚构桥有效预应力识别[J]. 铁道科学与工程学报,2011,8(6):12-16.
Zhang Z N, He S H, Zhao Y. Effective pre-stress iden?tification of the continuous rigid frame bridge in service based on inversion theory[J]. Journal of Railway Sci?ence and Engineering,2011,8(6):12-16.
[17] Lu Z R, Law S S. Identification of prestress force from measured structural responses[J]. Mechanical Systems and Signal Processing,2006,20(8):2186-2199.
[18] 卜建清,王海云 . PRC 简支梁桥有效预应力识别的 BP神 经 网 络 方 法[J]. 振 动 与 冲 击 ,2011,30(12):154-159.
Bu J Q, Wang H Y. Effective prestress identification for simple-supported PRC beam bridge by BP neural network method[J]. Journal of Vibration and Shock,2011,30(12):154-159.
[19] Hai Z, Yang M, Gao Z J. Dynamic responses of pre?stressed bridge and vehicle through bridge?vehicle inter?action analysis[J]. Engineering Structures,2015,87:116-125.
[20] Alamdari M M, Kildashti K, Samali B, et al. Damage diagnosis in bridge structures using rotation influence line: validation on a cable-stayed bridge[J]. Engineer?ing Structures,2019,185:1-14.
[21] Zhu Q, Xu Y L, Xiao X. Multiscale modeling and mod?el updating of a cable-stayed bridge. I: modeling and in?fluence line analysis[J]. Journal of Bridge Engineering,2015,20(10):04014112.
[22] Wu B, Wu G, Yang C, et al. Damage identification and bearing capacity evaluation of bridges based on dis?tributed long-gauge strain envelope line under moving vehicle loads[J]. Journal of Intelligent Material Sys?tems & Structures,2016,27(17):2344-2358.
[23] 邵旭东 . 桥梁工程[M]. 5 版 . 北京:人民交通出版社,2019.
Shao X D. Bridge Engineering[M]. 5th ed. Beijing:China Communication Press,2019.
[24] 王宁波,任伟新,何立翔 . 基于桥梁动力响应的应变影响线提取[J]. 中南大学学报(自然科学版),2014,45(12):4362-4369.
Wang N B, Ren W X, He L X. Extraction of strain in?fluence line of bridge from dynamic responses[J]. Jour?nal of Central South University(Science and Technolo?gy),2014,45(12):4362-4369.
[25] Wang N B, He L X, Ren W X, et al. Extraction of in?fluence line through a fitting method from bridge dynam?ic response induced by a passing vehicle[J]. Engineer?ing Structures,2017,151:648-664.
[26] Lu Z R, Law S S. Identification of prestress force from measured structural responses[J]. Mechanical Systems and Signal Processing,2006,20(8):2186-2199.
[27] 李鎮,孙智 . 基于强迫振动测试的预应力混凝土梁桥承 载 力 评 估[J]. 华 中 科 技 大 学 学 报(城 市 科 学 版),2008,25(3):172-176.
Li Z, Sun Z. Load carrying capacity assessment of pre?stressed concrete beam bridge based on structural forced vibration response[J]. Journal of Huazhong University of Science and Technology (Urban Science Edition),2008,25(3):172-176.

