纯电动汽车悬置系统固有特性的不确定性和相关性传播分析

吕辉 李振聪 杨坤 黄晓婷 上官文斌

摘要： 针对纯电动汽车动力总成悬置系统（Powertrain Mounting System，PMS）参数同时存在不确定性和相关性的情形，开展了纯电动汽车 PMS 固有特性的不确定性和相关性传播分析研究。利用多维平行六面体模型量化系统参数不确定性和相关性；基于多维平行六面体模型，将正则化法、泰勒展开法及中心差分法相结合，提出了一种 PMS固有特性响应不确定性传播分析的 MP 摄动法。结合系统固有特性响应数据，基于蒙特卡罗法和置信度，提出了一种系统固有特性响应的相关性传播分析方法。以某纯电动汽车 PMS 算例验证了方法的有效性。分析结果表明：系统参数的不确定性会使得系统响应具有不确定性，而系统参数的相关性会使得系统响应具有一定的相关性。

关键词： 纯电动汽车；动力总成悬置系统；多维平行六面体模型；不确定性传播；相关性传播

中图分类号： U469.72 文献标志码： A 文章编号： 1004-4523（2023）03-0671-09

DOI：10.16385/j.cnki.issn.1004-4523.2023.03.009

引 言

在纯电动汽车的设计、制造和工作过程中，广泛地存在着各种不确定因素。纯电动汽车的动力源采用驱动电机取代了发动机，发动机的“掩蔽效应”消失，使得各种不确定因素相互作用下的纯电动汽车噪声 、振动和声振粗糙度（Noise，Vibration and Harshness，NVH）问题更加突出。动力总成悬置系统（Powertrain Mounting System，PMS）作 为 NVH技术的重要一环，是纯电动汽车隔离振动传递、降低噪声传播的重要系统之一［1？2］。对纯电动汽车 PMS固有特性开展不确定性领域方面的分析研究具有重要的工程意义。

近年来，针对 PMS 固有特性开展的不确定性研究已经很成熟。辛付龙等［3］以悬置刚度为优化变量并考虑其不确定性，以系统解耦率、悬置动反力以及动反力的稳健性函数为优化目标，对 PMS 进行了多目标稳健优化；刘春梅等［4］考虑了悬置刚度的制造误差等不确定因素，提出了一种 PMS 的可靠设计流程，并将其用于某悬置系统的开发设计；谢展等［5］基于区间分析，将稳健设计与多目标优化相结合，提出了一种PMS隔振性能的稳健优化设计方法 ；Cai等［6］针对 PMS 一部分参数信息匮乏而另一部分參数信息充足的复杂情形，构建随机与区间混合模型对 PMS 固有特性进行了不确定性传播分析和优化设计。

上述研究均将系统不确定参数视为独立变量。在实际工程中，机械系统的关键参数之间往往具有一定相关性，不确定参数间的相关性研究已经受到越来越多学者的关注。Qiu 等［7］对比分析了考虑参数相关性的椭球模型和未考虑参数相关性的区间模型在结构动力学响应分析中的应用。吕辉等［8］提出了一种基于多椭球凸模型的 PMS 固有特性的不确定性传播分析方法，分析了刚度参数相关性对系统响应的影响。然而，单个椭球凸模型仅能处理所有不确定参数完全相关的情形。当系统参数一部分独立、另一部分相关时，采用椭球凸模型需要分组建立多个椭球，过程相对复杂［9］。近年来，多维平行六面体（Multidimensional Parallelepiped，MP）模 型 备 受关注，该模型可以对不确定参数完全独立，完全相关，或者既有相关性又有独立性的各种情形进行量化。因此，吕辉等［10］进一步引入 MP 模型处理 PMS参数相关性和独立性并存的情形，结合蒙特卡罗法初步提出了一种 PMS 的不确定性传播分析方法。

可以看出，考虑不确定参数相关性的 PMS 研究已受到学者的密切关注，并取得了一些成果。对此，可能还存在两方面的关键问题需解决。第一，目前基于 MP 模型的 PMS 不确定性传播分析主要依赖于蒙特卡罗抽样［10］，其计算效率相对较低。第二，在纯电动汽车 PMS 中普遍采用的橡胶悬置的三向刚度参数之间存在明显的相关性。系统参数的相关性必然会引起系统响应之间存在一定的相关性，即相关性传播现象［11］，现有研究尚未开展这方面工作。

针对上述问题，本文旨在开展纯电动汽车 PMS固有特性的不确定性传播和相关性传播分析研究。首先引入 MP 模型描述 PMS 中存在不确定性和相关性的刚度参数，随后提出一种能快速求解系统固有特性响应区间的不确定性传播分析方法；接着提出一种基于蒙特卡罗法的相关性传播分析方法。最后，通过数值算例验证方法的有效性。

1 分析模型

1. 1 纯电动汽车 PMS 模型

图 1 为某纯电动汽车 PMS 的三维模型及其对应的六自由度动力学模型［12］。一般可将动力总成简化为六自由度刚体，橡胶悬置元件简化为具有三向正交刚度的弹簧模型。

1. 2 不确定性分析模型

工程实际中，存在一种典型的“多源不确定性”问题［13］，即参数的不确定性来源可能不同。同一来源时，不确定参数可能是相关的；不同来源时则是独立的。如纯电动汽车 PMS 中，同一橡胶悬置的三向刚度参数存在一定的相关性，而不同悬置的参数之间则是相互独立的。利用 MP 模型［14］，可以描述参数相关性和独立性共存的复杂情形。

对任意两个相互独立的不确定参数 Xt 和 Xl 的取值范围（t，l = 1，2，？，n 且 t ≠ l）可以建立一个矩形不确定域 ΩS，如图 2 中虚线所示。若 Xt 和 Xl 之间存在相关性，则可用图 2 中实线所围的平行四边形域 Ω 表示。

2 PMS 不确定性传播分析

由于系统参数是不确定的，计算得到的系统响应也是不确定的，这就是不确定性传播问题。对于PMS 固有特性的不确定性传播分析，文献［10］基于蒙特卡罗法开展了初步研究。在此基础上，本节将提出一种快速求解系统响应的 MP 摄动法。

首先将描述纯电动汽车系统参数的 MP 模型转换为正则区间模型。正则化可以通过下式实现：

3 PMS 相关性传播分析参考文献［10］，基于蒙特卡罗法可求得纯电动汽车 PMS 固有特性的一系列响应数据。记任意两个响应分别为 Ft（ X ） 和 Fl（ X ） （t，l = 1，2，？，6），且均有 B 组响应数据 FtS =[ F（1） t ，F（ 2） t ，？，F（ B） t ]和 FlS =[ F（1） l ，F（ 2） l ，？，F（ B） l ]。 由 于 相 关 性 传 播 ，FtS 和 FlS 会呈现出一定的相关性。

基于蒙特卡罗法求解 FtS 和 FlS 的相关性，主要步骤如下：

（5）以一微小增量 Δt 对变量 t 进行迭代计算，直到得到包络 FtS 和 FlS 所有样本点的平行四边形不确定域，以及最终的相关系数 ρFt Fl。

建立包络 FtS 和 FlS 所有样本点且面积最小的平行四边形域非常耗时，且会在平行四边形域内留下没有样本的大量空白区域［15］。此时，可以引入置信度 τ = H B。其中，H 为被平行四边形不确定域包络的样本数；B 为样本总数。因此，在上述步骤（5）中，当被包络的样本数与样本总数的比值达到所设置信度 τ 时，即可作为迭代过程结束的条件。

一般地，分散的样本对应一个大的置信度，可以使构成的平行四边形不确定域对样本的包络更合理，避免不确定量化结果面临高风险；而聚集的样本对应一个小的置信度，可以避免平行四边形不确定域出现许多空域。

图 5 给出了 PMS 相关性传播分析的一般流程。

4 算例分析

4. 1 PMS 分析模型

以某纯电动汽车 PMS 为例，其模型示意图如图6 所示。电机总成重为 82 kg。表 1 为电机总成的转动惯量和惯性积。表 2 为悬置的初始刚度。表 3 为悬置的安装位置。悬置为水平安装。

4. 2 不确定性传播分析

由于 θ（x 绕电机转子旋转方向）、Y（汽车前进方向的左右侧）和 Z（竖直方向）方向为电机总成振动有特性。这三个方向的固有频率分别记为 F Y，FZ 和Fθx，解耦率分别记为 D Y，DZ 和 Dθx。

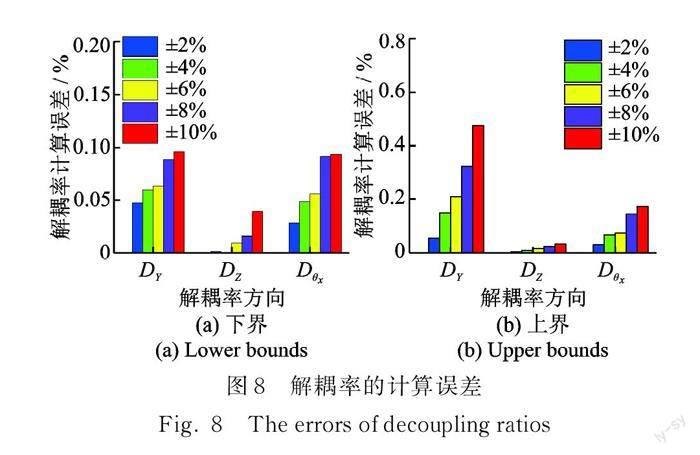
纯电动汽车 PMS 的橡胶悬置刚度参数具有较明显的不确定性和相关性。定义表 2 中的悬置刚度值为其不确定取值区间的中心点，并将其由中心点变化的百分比作为不确定度。为便于分析，本算例给定同一悬置刚度参数的相关系数为 0.4，不同悬置间的刚度参数相互独立。当刚度参数的不确定度依次为±2%， ±4%， ±6%， ±8% 和±10% 时，利用提出的 MP 摄动法计算 PMS 固有特性，结果如表 4所示。以蒙特卡罗法抽样 106次求得的系统固有特性结果作为参考，如表 5 所示。将两种方法计算结果之差的绝对值作为 MP 摄动法的计算误差。不同情形下 MP 摄动法的计算误差如图 7 和 8 所示。

由表 4 和 5 可知，由于不确定性传播，悬置刚度的不确定性导致系统固有特性也是不确定的。随着系统参数不确定度增大，固有特性的区间范围也在增大，呈现向外扩张趋势。

由图 7 可知，对于固有频率下界，MP 摄动法的计算误差随着参数不确定度增大而增大，最大误差约为 0.28 Hz，出现在 θ x 方向，此时对应的参数不确定度为±10%，而 Y 和 Z 方向固有频率下界的计算误差均较小。对于固有频率上界，MP 摄动法计算的最大误差约为 0.34 Hz，仍出现在 θ x 方向且对应的参数不确定度为±10%。当不确定度小于±10%时，Y 和 Z 方向的计算误差均小于 0.1 Hz。

由图 8 可知，对于解耦率下界，MP 摄动法计算的最大误差出现在 Y 方向上，最大误差约为 0.1%，对应的参数不确定度亦为±10%。对于解耦率上界，MP 摄动法计算的最大误差仍出现在 Y 方向，最大 误 差 约 为 0.5%，对 应 的 参 数 不 确 定 度 也 为±10%。

对于上述不确定性传播分析，每种不确定度情形下的蒙特卡罗法均基于随机抽样，需要大量抽样运算才能得到精确的不确定响应结果，因此其计算效率较低，计算时间约为 2923 s；而 MP 摄动法基于正则化法、泰勒展开法及中心差分法，其计算不确定响应边界时，仅需根据推导的公式进行运算，因此计算效率很高，计算时间约为 3.1 s.

因此，本文提出的 MP 攝动法，在纯电动汽车PMS 固有特性的不确定性传播分析中，不仅具有较高的计算精度，而且还具有很高的计算效率。

4. 3 相关性传播分析

由于系统参数具有相关性，计算得到的系统响应之间也会具有一定的相关性，这就是相关性传播问题。本节进一步研究系统参数相关性对输出响应相关性的影响，即开展相关性传播分析。

给定刚度参数的不确定度为 ±8%，每个悬置任意两个刚度之间的相关系数记为 ρ0。 此外 ，以ρ （ Fi，Fj） （i，j = Y，Z，θ x，i ≠ j） 表示任意两个方向固有 频 率 之 间 的 相 关 系 数 ；以 ρ （ Di，Dj） （i，j =Y，Z，θ x，i ≠ j） 表示任意两个方向解耦率之间的相关系数；ρ （ Fn，Dm ） （ n，m = Y，Z，θ x ） 表示固有频率和解耦率之间的相关系数。

研究 ρ0=0.3，0.5 和 0.7 三种情形，利用提出的相关性传播分析方法分别计算系统固有特性响应之间的相关系数，结果如表 6～8 所示。

由表 6～8 可知：

（1）当刚度参数的相关系数相同时，不同方向固有频率之间的相关性最高，解耦率与固有频率之间的相关性最低，不同方向解耦率之间的相关性介于两者之间；

（2）随着刚度参数相关系数增大，固有特性之间的相关性有可能随之增大（如 ρ （ ） F Y，FZ ，ρ （ ） F Y，Fθx ，ρ （ FZ，Fθx ） 和 ρ （ D Y，DZ ）），也有可能随之减 （如ρ （ FZ，DZ ） 和 ρ （ Fθx，DZ ）），或 者 先 增 大 后 减 小（如ρ （ F Y，D Y ），ρ （ F Y，DZ ），ρ （ F Y，Dθx ），ρ （ FZ，Dθx ） 和ρ （ Fθx，Dθx ））。

利用提出的相关性传播分析法，还可以建立不同情形下任意两个固有特性响应之间的平行四边形不确定域，如图 9 和图 10 所示。由前面分析可知，固有频率和解耦率之间的相关性较低，故它们之间的响应相关性不再讨论。限于篇幅，仅给出F Y 和 FZ，以及 DZ 和 Dθx 响应数据的平行四边形不确定域。

由图 9 和图 10 可知：

（1）对于固有频率响应 ，F Y 和 FZ 之间的样本数据呈正相关性，且随着刚度参数相关系数增大，响应样本数据变得越聚集 ；即它们之间的相关系数越大 ，所构成的平行四边形不确定域越狭窄 。此时，若要对系统固有频率进行优化设计，应充分考虑它们之间的相关性，以获得更合理结果。

（2）对于解耦率响应，DZ 和 Dθx 呈现出较低的相关性，随着刚度参数相关系数增大，响应样本数据分布范围变化不大，均较为分散；即它们之间的相关系数变化不大且数值较小，所构成的平行四边 形 不 确 定 域 面 积 较 大 ，接 近 于 矩 形 不 确 定 域 。此时，若要对系统解耦率进行优化设计，可以忽略DZ 和 Dθx 之间的相关性，以达到简化问题的目的。5 结 论针对纯电动汽车 PMS 参数同时存在不确定性和相关性的复杂情形，基于多维平行六面体模型分别提出了系统固有特性的不确定性传播分析方法和相关性传播分析方法。算例分析表明：（1）在不确定性传播分析方面，所提出的 MP 摄动法具有计算误差小和计算效率高的特点；（2）在相关性传播分析方面，所提出的分析法能有效求得系统响应之间的相关系数，以及响应样本的平行四边形不确定域；（3）随着系统参数不确定度增大，固有频率和解耦率响应的区间范围逐渐增大；固有频率之间的相关性最高，解耦率与固有频率之间的相关性最低，解耦率之间的相关性介于两者之间。

参考文献：

［1］ 康强，顾鹏云，左曙光 . 纯电动汽车电驱动总成悬置设 计 原 则 研 究［J］. 汽 车 工 程 ，2019，41（11）：1235？1242.

Kang Qiang， Gu Pengyun， Zuo Shuguang. A research on design principles for electric drive assembly mounts of pure electric vehicles［J］. Automotive Engineering，2019，41（11）：1235？1242.

［2］ 栾英林，崔华阁，贾旭东 . 纯电动乘用车动力总成悬置系统优化设计［J］. 重庆理工大学学报（自然科学），2020，34（6）：90？96.

Luan Yinglin， Cui Huage， Jia Xudong. Optimum de？sign of powertrain mounting system for pure electric pas？senger vehicle［J］. Journal of Chongqing University of Technology （Natural Science），2020，34（6）：90？96.

［3］ 辛付龙，钱立军，方驰 . 纯电动汽车动力总成悬置系统的多目标稳健优化设计［J］. 汽车技术，2016（8）：1？5.

Xin Fulong， Qian Lijun， Fang Chi. Multi？objective ro？bust optimization design of powertrain mount system for electric vehicle［J］. Automotive Technology，2016（8）：1？5.

［4］ 刘春梅，黄德惠，郑成，等 . 动力总成悬置系统的可靠设计［J］.中国机械工程，2020，31（21）：2529？2534.

Liu Chunmei， Huang Dehui， Zheng Cheng， et al. Reli？able design of PMSs［J］. China Mechanical Engineer？ing，2020，31（21）：2529？2534.

［5］ 謝展，于德介，李蓉，等 . 基于区间分析的发动机悬置系 统 稳 健 优 化 设 计［J］. 汽 车 工 程 ，2014，36（12）：1503？1507.

Xie Zhan， Yu Dejie， Li Rong， et al. Robust optimiza？tion design of engine mount system based on interval analysis［J］. Automotive Engineering，2014，36（12）：1503？1507.

［6］ Cai B， Shangguan W B， Lü H. An efficient analysis and optimization method for the powertrain mounting system with hybrid random and interval uncertainties［J］. Engi？neering Optimization，2020，52（9）：1522？1541.

［7］ Qiu Z， Wang X. Parameter perturbation method for dy？namic responses of structures with uncertain？but？bounded parameters based on interval analysis［J］. International Journal of Solids & Structures， 2005， 42（18？19）：4958？4970.

［8］ 吕辉，杨坤，上官文斌，等 . 考虑不确定参数相关性的动力总成悬置系统固有特性分析［J］. 振动工程学报，2020，33（6）：1199？1207.

Lü Hui， Yang Kun， Shangguan Wenbin， et al. Inherent characteristics analysis of powertrain mounting systems considering the correlation of uncertain parameters［J］.Journal of Vibration Engineering， 2020， 33 （6） ：1199？1207.

［9］ 贾爱芹，陈建军，徐亚兰 . 基于摄动法的不确定性汽车悬架振动控制特征值的凸模型分析［J］. 中南大学学报（自然科学版），2012，43（4）：1320？1324.

Jia Aiqin，Chen Jianjun，Xu Yalan. Convex model analy？sis of vibration control eigenvalues of vehicle suspension system based on perturbation method［J］. Journal of Central South University （Science and Technology），2012，43（4）：1320？1324.

［10］ 吕辉，杨坤，尹辉，等 . 基于多维平行六面体模型的动力总成悬置系统固有特性分析［J］. 汽车工程，2020，42（4）：498？504.

Lü Hui， Yang Kun， Yin Hui， et al. Inherent character？istic analysis of powertrain mounting system based on multidimensional parallelepiped model［J］. Automotive Engineering，2020，42（4）：498？504.

［11］ Ouyang H， Liu J， Han X， et al. Correlation propaga？tion for uncertainty analysis of structures based on a non？probabilistic ellipsoidal model［J］. Applied Mathe？matical Modelling，2020，88：190？207.

［12］ 黄家铭，田晋跃，陈治领 . 純电动客车电机动力总成悬置系统的优化设计［J］. 噪声与振动控制，2016，36（4）：108？112.

Huang Jiaming， Tian Jinyue， Chen Zhiling. Optimal de？sign of powertrain mount systems of electric bus motors［J］. Noise and Vibration Control， 2016， 36（4）：108？112.

［13］ 王攀，臧朝平 . 改进的平行六面体凸模型识别动力学不确定参数区间的方法［J］. 振动工程学报，2019，32（1）：97？106.

Wang Pan， Zang Chaoping. Method of identifying dy？namic uncertain parameter intervals with improved par？allelepiped convex model［J］. Journal of Vibration Engi？neering，2019，32（1）：97？106.

［14］ Ni B Y， Jiang C， Han X. An improved multidimension？al parallelepiped non？probabilistic model for structural uncertainty analysis［J］. Applied Mathematical Model？ling，2016，40（7？8）：4727？4745.

［15］ Wang C， Matthies H G. A modified parallelepiped mod？el for non？probabilistic uncertainty quantification and propagation analysis［J］. Computer Methods in Applied Mechanics and Engineering，2020，369：113209