直升机超临界尾传动轴限幅减振器非线性动力学特性研究
王旦 宋立瑶 陈柏 李波 朱如鹏 吴洪涛

摘要: 直升机超临界尾传动轴在跨临界转速时会产生剧烈的振动。限幅减振器是专门针对尾传动轴跨临界减振问题设计的一种复合式减振器。限幅减振器与尾传动轴组成的系统具有摩擦、碰撞等强非线性特征,动力学特性异常复杂。为揭示限幅减振器工作机理并指导减振器设计,建立了具有双间隙结构的限幅减振器与尾传动轴系统的弹簧质量阻尼等效模型。分别基于直接时间域积分和时频变换谐波平衡(Harmonic Balance Method with Alternating FrequencyTime Domain Technique)+数值延拓(Numerical Continuation)两种方法对控制方程进行了求解。计算结果表明,限幅减振器存在无作用、正常减振、异常减振、限位四种工作状态。其中,限位状态是针对故障工况下尾传动轴进行的临时限位保护。此外,进一步研究了减振器参数对减振和限位效果的影响,得到了传动轴与碰摩环之间间隙、碰撞刚度以及临界摩擦力对限幅减振器减振效果的影响规律。发现存在最优临界摩擦力,且最优临界摩擦力与传动轴不平衡量等有关。同时限位状态下,通过增加碰摩环与底座之间的碰撞刚度可以减小限位幅值,但也会产生更大的冲击力。最后,开展了正常减振工况下碰摩间隙和临界摩擦力两个关键参数对限幅环减振效果影响的试验研究,验证了模型的有效性。
关键词: 超临界尾传动轴;限幅减振器;双间隙;干摩擦;限位保护
中图分类号: V214.19 文献标志码: A 文章编号: 1004-4523(2023)03-0593-13
DOI:10.16385/j.cnki.issn.1004-4523.2023.03.001
1 概 述
传动系统是直升机三大动部件之一,主要由三器两轴即主减速器、中间减速器、尾减速器、动力传动轴及尾传动轴组成[1]。其中,尾传动轴将主减速器尾输出动力经由中间减速器再传给尾减速器以驱动尾桨,是连接主、中、尾减速器的重要部件。直升机尾传动轴有两种设计方案[2]:一是亚临界设计,尾传动轴的最大工作转速低于一阶临界转速,并有一定的安全裕度;二是超临界设计,尾传动轴的工作转速位于一阶临界转速与二阶临界转速之间。采用亚临界方案时,为了提高尾传动轴的一阶临界转速以保证在最大工作转速之上,需设置较多的轴段[3]及轴承支点,增加了传动系统的成本和重量。这对直升机来说是不利的。传统的直升机,如法国的“超黄蜂”、美国的“黑鹰”等采用了亚临界设计。超临界设计允许传动轴的跨度很大,减少了支承数量,使得尾传动轴系结构简单,重量和成本都相应减小。因此,超临界尾传动轴能更好地满足直升机的发展需求。目前超临界方案已经成为直升机传动轴系设计的一种趋势。阿古斯塔 AB129、欧直 EC175 等先进直升机的尾传动轴均采用了超临界设计[4]。但超临界设计意味着尾传动轴必须跨过一阶临界转速,而尾传动轴由于存在不平衡量,跨临界转速时会产生剧烈的横向振动,使尾轴受到巨大的作用力,甚至破坏失效,严重影响到尾传动轴系的寿命和安全。因此针对超临界设计带来的振动问题,开展直升机超临界尾传动轴跨临界转速减振技术研究具有重要意義。
目前针对尾传动轴的减振手段主要有支承减振器和限幅减振器。支承减振器主要包括实心橡胶减振器和橡胶硅油组合式黏弹性减振器。其中橡胶硅油组合式黏弹性减振器采用空心橡胶环结构,环腔内充满对温度变化不敏感的硅油[5]。支承减振器通常安装在传动轴系的轴承与轴承座之间,通过自身的阻尼对传动轴减振。但对于超临界尾传动轴,其传动轴较长,轴承之间跨度较大,仅在支承处安装减振器,减振效果有限。因此通常需要在轴段中间处进一步安装限幅减振器,如图 1 所示,限幅减振器能有效抑制尾传动轴跨临界转速时的横向振动。
由于限幅减振器是针对传动轴跨临界转速设计的,因此一方面要求限幅减振器在传动轴跨临界转速时能起到很好的减振作用,另一方面当传动轴到达工作转速后,限幅减振器将不再工作,以避免对尾传动系统的正常运转造成影响。这也是限幅减振器不同于其他减振器的独特之处。
国内外对于限幅减振器已经开展了一些相关研究工作。zaydn 等[67]基于谐波平衡法研究了限幅减振器的非线性动力学特性,得到了传动轴的幅频特性曲线,在此基础上分析了摩擦阻尼、减振器的分布位置以及减振器与传动轴之间间隙对减振效果的影响。Dygado 等[8]建立了尾传动轴系和限幅减振器的动力学模型,着重研究了间隙对减振效果的影响,得出了带间隙的限幅减振器减振效果更佳的结论。但上述研究均只分析了转轴与减振器之间的单间隙影响,减振器自身结构中所包含的第二重间隙的动力学影响未被考虑。Huang 等[9]建立了考虑双间隙结构的限幅减振器动力学模型,进行了传动轴系的动力学响应特性分析。但其所建立的模型耦合了过多不相关因素,导致其对减振器基本工作原理的分析不够清晰,难以有效指导减振器设计和改型。此外,复合材料传动轴相比于传统铝轴具有更高的比强度、比刚度[10],可以进一步减轻传动系统的重量,因此得到了越来越多的研究和应用。Spears[11]针对贝尔 429 直升机的复合材料超临界尾轴设计了限幅减振器,介绍了减振器基本组成,但其并未开展减振器基本工作原理和非线性动力学方面的研究。综上可知,当前关于限幅减振器的研究虽取得了一定成果,但相关研究存在模型结构不完善或者耦合了过多不相关因素等问题,尚未厘清限幅减振器的基本工作原理,未能有效揭示减振器工作过程中独特的非线性动力学特性及其影响因素。因此,本文聚焦于减振器的基本工作原理,建立兼具双间隙结构及干摩擦特征的限幅减振器非线性动力学模型,并详细分析限幅减振器关键参数对减振效果的影响,为限幅减振器设计和改型提供理论支持。
2 传动轴及限幅减振器系统动力学模型
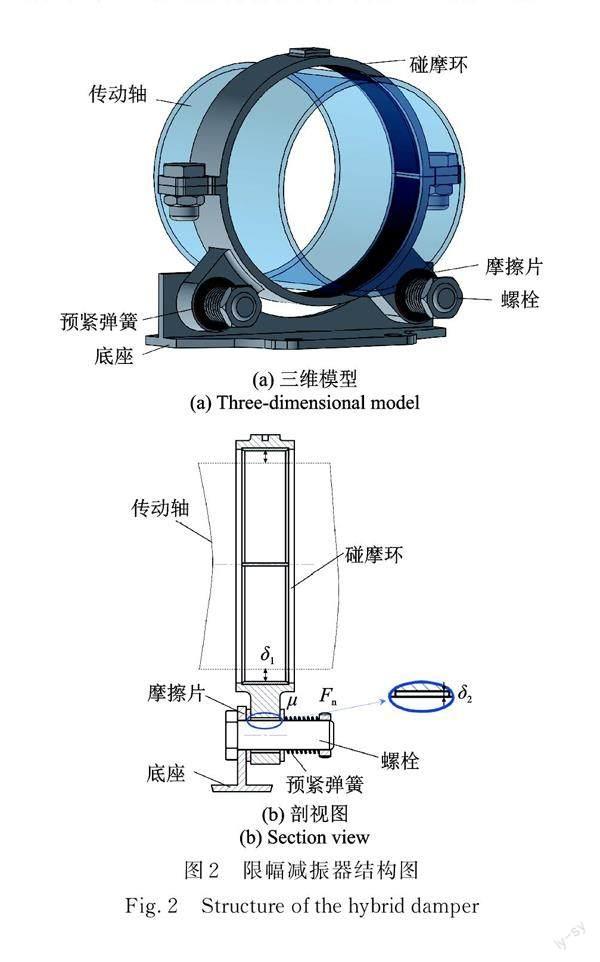
限幅减振器主要由碰摩环、预紧弹簧、摩擦片、螺栓及底座等组成,详细结构如图 2 所示。为方便尾轴安装,碰摩环分为上下两部分,中间通过螺栓进行连接。传动轴安装在碰摩环内部,与碰摩环之间预留间隙 δ1。下方碰摩环两侧安装有四个摩擦片,其与碰摩环之间的摩擦系数为 μ,通过两个螺栓将碰摩环和摩擦片安装在底座上,并使碰摩环与螺栓之间预留间隙 δ2,如图 2(b)所示。在螺栓上安装预紧弹簧,通过预紧弹簧向摩擦片施加预紧力 Fn。
当传动轴跨临界转速产生剧烈的横向振动时,传动轴超越间隙 δ1 与碰摩环产生碰撞。在碰撞力的作用下,碰摩环发生移动,与摩擦片之间产生干摩擦,引入摩擦阻尼。当碰摩环超越间隙 δ2 后将与底座碰撞,发生第二个碰撞过程,产生限位作用。
2. 1 弹簧质量阻尼等效模型
限幅减振器与传动轴系统是一个具有强非线性的系统,其动力学行为非常复杂。为了厘清其内在的减振机理 ,对系统进行简化,建立等效弹簧质量阻尼模型,在此等效模型的基础上进行非线性动力学特性分析。
由于限幅减振器主要工作在尾轴的一阶临界转速附近,因此传动轴的动力学可由单自由度弹簧质量阻尼模型等效,其等效质量为 meq,1,等效刚度为k eq,1,等效阻尼为 c eq,1。采用带有黏性阻尼的线性碰撞力模型,可将碰撞过程等效为与弹簧阻尼等效碰撞模块之间的相互作用。因此碰摩环可等效为带有上下两个弹簧阻尼碰撞模块的质量块,其质量为meq,2,同样固定底座也带有上下两个弹簧阻尼碰撞模块,最终得到传动轴与限幅减振器系统的等效弹簧质量阻尼模型,如图 3 所示。以向上为正方向,以对称位置为位移原点,设传动轴的位移为 u 1,碰摩环的位移为 u 2。传动轴与碰摩环之间的碰撞力为F N,1,碰撞刚度和碰撞阻尼分别为 k 1 和 c 1。碰摩环与螺栓之间的碰撞力为 F N,2,碰撞刚度和碰撞阻尼分别为 k 2 和 c2。碰摩环与摩擦片之间的摩擦力为 Ff。
根据传动轴与碰摩环的相对运动及位置关系,可以得到系统的四种不同运动状态。
第一种:u 1 与 u 2 之差的绝对值小于 δ1,传动轴未与碰摩环碰撞,减振器不起作用。
第二种:u 1 与 u 2 之差的绝对值超过 δ1,传动轴与碰摩环碰撞,且碰撞力不足以使碰摩环克服最大静摩擦力。
第三种:碰摩环突破最大静摩擦力而产生运动,摩擦力由静摩擦力转变为滑动摩擦力。但 u 2 小于δ2,碰摩环未和底座碰撞。
第四种:u 2 超过 δ2,碰摩环与底座碰撞。
2. 2 系统非线性动力学方程
为了得到传动轴与碰摩环的动力学方程,分别对传动轴和碰摩环进行受力分析,再基于摩擦力模型和碰撞力模型,建立系统的非线性动力学方程组。
根据限幅减振器的组成及工作原理分析,系统在工作过程中会发生两个碰撞过程,分别是传动轴与碰摩环之间的碰撞、碰摩环与底座之间的碰撞。传动轴只受到第一个碰撞力及偏心激励的作用,动力学方程为:
本文主要关注传动轴跨临界转速过程中的动力学响应,因此将传动轴转速从零转速加速到稳定工作转速。在加速过程中,传动轴的加速度由切向加速度和向心加速度两部分合成,设传动轴的角加速度为 α,偏心距离为 e,则切向加速度为 eα,向心加速度为 e ( αt )2;当加速到稳定运行频率后,切向加速度为零,只存在向心加速度。因此将传动轴加速度产生的惯性力向竖直方向分解,可得到偏心激励力 Fe的表达式如下[12]:式中 ωs 为传动轴稳定运转频率。碰摩环受到两个碰撞力及摩擦力的作用,动力学方程为:式(1)和(3)即组成传动轴与减振器系统的动力学控制方程,求解微分方程组即可得到传动轴的动力学响应。
2. 3 碰撞力模型
转子与定子之间的碰摩问题一直是旋转机械方面的研究重点,产生了很多碰摩力计算模型,其中分段线性弹簧是最常用的一种计算法向碰摩力的模型。本文采用同时考虑法向力和法向阻尼的线性弹簧碰撞力模型[13]实现对两个碰撞力的计算。碰撞力模型如下式所示:
F N = kε + cε (4)式中 k 为法向碰摩刚度;c 为接触碰撞的法向黏性阻尼系数[14]:式中 a 为经验系数;ε 为转子与定子之间的侵入位移。
设传动轴对碰摩环的侵入位移为 ε1。当传动轴对碰摩环产生侵入时,即 |u 1 - u 2 | - δ1 > 0,存在两种情况:若在传动轴上方产生侵入,即 u 1 > u 2,此时ε1 = u 1 - u 2 - δ1;若 在 传 动 轴 下 方 产 生 侵 入 ,即u 1 < u 2,此时 ε1 = u 1 - u 2 + δ1。当传动轴未侵入碰摩环时,即 |u 1 - u 2 | - δ1 ≤ 0,此时 ε1 = 0。可得 ε1 的表达式如下:设碰摩环对底座的侵入位移为 ε2。同理,可得ε2 的表达式如下:将 侵 入 位 移 ε1,ε2 代 入 式(4),即 可 得 到 F N,1,F N,2 的表達式。
2. 4 干摩擦模型
采用库伦摩擦模型计算碰摩环与摩擦片之间的干摩擦力,假设动静摩擦系数相等,且滑动摩擦系数与两固体接触表面相对运动速度无关而保持恒定。库伦摩擦模型[15]表达式如下:式中 Ff 为摩擦力;μ 为滑动摩擦系数;Fn 为接触面之间的正压力;v 为两固体接触表面的相对滑动速度。由于摩擦片固定,因此碰摩环与摩擦片之间的相对滑动速度即为碰摩环的速度 u 2。
2. 5 模型求解方法
首先,为了获得传动轴与减振器系统的时间域非线性动力学响应,可以直接通过数值积分法对式(1)和(3)所构成的微分方程组进行求解。考虑到系统方程为典型的刚性方程 ,本文直接采用 MATLAB 内置的 ode15s 求解器进行求解[16]。此外,基于时频变换谐波平衡和数值延拓技术,可直接获得系统的幅频特性曲线,其中包含了更丰富的系统动力学信息。
对于一般形式的 NDOF 自由度的非线性机械系统,其控制方程可写成如下形式:
谐波平衡法假设在周期 T 的基础激励下,系统响应可近似表示成截断形式的傅里叶级数:式中 H 为傅里叶级数的截断阶数;u(0),uc( k) 和us( k) 分别为常数项、k 阶余弦和正弦谐波系数;Ω =2π/T 为基础激励频率。式中 rl,H,rnl,H 和 rex,H 分别为线性项、非线性项和激励项对应的残差谐波系数。线性项 rl,H 和激励项rex,H 容易获得。对于 rnl,H,多项式型非线性项一般可以通过三角函数变换直接获得。对于本文中所讨论的间隙和干摩擦等更一般形式的非线性项,其处理需借助于时频变换技术。首先,通过傅里叶逆变换将 uH 转换到时间域,基于非线性项的时域表达式获得其对应的残差,进一步借助傅里叶正变换获得该时域残差项的前 H 阶谐波系数 rnl,H,更详细的时频变换谐波平衡法可参考文献[1719]。
求解代数方程(13)即可获得谐波系数 uH,进而获得基础激励频率为 Ω 时系统的响应 u (t)。但由于非线性项的存在,一般无法获得代数方程(13)的解析解,因此只能采用数值计算方法。理论上,通过连续改变基础激励频率 Ω,可获得不同激励频率下系统的响应,进而获得系统的幅频特性曲线。然而对于非线性系统,其幅频特性曲线可能存在分叉点、拐点等特殊点,为了能够顺利通过这些特殊点,需要进一步借助数值延拓技术。若已知非线性代数方程某个解,数值延拓技术可通过估计修正两步法,自动获得解分支上的下一个解。通过连续的数值延拓,便可获得整条幅频特性曲线,具体过程可参考文献[1719]。
3 系统响应结果分析
3. 1 仿真参数
采用某型直升机传动轴参数进行数值仿真[20],传动轴参数如表 1 所示。
将表 1 中的参数代入式(14)~(17)中,得到传动轴的等效质量、等效刚度及等效阻尼。进一步结合设计经验,得到如表 2 所示的仿真参数。若无特殊说明,下文均采用表 2 所示参数进行仿真。
3. 2 限幅减振器工作状态分析
仿真表明,在表 2 所列参数下,随着传动轴不平衡量的增大,限幅减振器主要存在四种工作状态,分别为无作用状态(mode Ⅰ)、正常减振状态(mode Ⅱ)、异 常 减 振 状 态(mode Ⅲ)及 限 位 状 态(mode Ⅳ),如图 4 所示。本节将通过改变传动轴的不平衡量,得到四种状态下传动轴的典型响应,并对响应结果进行详细分析。
3. 2. 1 无作用状态响应
图 5给出了限幅减振器无作用时传动轴的典型响应结果,其中传动轴的不平衡量设置为 0.1 kg·mm。图中红色虚线表示传动轴与碰摩环之间的间隙 δ1,绿色虚线表示 δ1 和碰摩环与底座之间的间隙 δ2 之和,黑色竖虚线为传动轴加速到工作转速的时间节点,此后将保持工作转速不变。从图 5 中可以看出,传动轴的振动幅值在整个时间历程中都处于 δ1 之下,因此限幅减振器未对传动轴产生任何作用。
3. 2. 2 正常减振状态响应
正常减振状态下,限幅减振器主要是利用传动轴与碰摩环之间的碰撞及干摩擦组合作用进行减振。图 6 给出了限幅减振器正常减振状态时传动轴的典型响应结果,其中传动轴的不平衡量设置为0.6 kg·mm。作为参考,图中黑色曲线为未安装减振器时传动轴的振动响应。
可以看出,在此不平衡量下传动轴的共振幅值已经超过了 δ1 的范围,限幅减振器对传动轴产生了作用,但碰摩环与底座之间的二次限位碰撞未发生。仿真计算表明,传动轴在未安装限幅减振器时的共振幅值为 5.0035 mm,在限幅减振器正常减振状态下的共振幅值仅为 1.3118 mm,幅值减小了 74%。并且当传动轴加速到工作转速后,振动幅值下降到δ1 以下,减振器不再工作。在正常减振状态下,限幅减振器利用传动轴与碰摩环之间的单间隙碰撞及干摩擦能对传动轴起到良好的减振效果,且不影响传动轴工作转速下的稳定运转。
3. 2. 3 异常减振状态响应
在正常减振状态的基础上进一步增大不平衡量,限幅减振器就会进入异常减振状态。此时限幅减振器仍然利用传动轴与碰摩环之间的单间隙碰撞及干摩擦进行减振,但当传动轴加速到工作转速时,传动轴依旧会和减振器发生碰摩。图 7 给出了限幅减振器处于异常减振状态时的传动轴典型响应结果,其中传动轴的不平衡量设置为 1.6 kg·mm。作为参考,图中黑色曲线为无减振器时传动轴的振动响应。
仿真计算表明,传动轴在未安装限幅减振器时的共振幅值为 13.343 mm,在限幅减振器减振状态下的共振幅值为 2.0555 mm,幅值减小了 85%。在此不平衡量下,虽然限幅减振器可以对传动轴起到有效减振作用,但当传动轴加速到工作转速后,传动轴的振幅仍然超出了 δ1 的范围,传动轴与减振器之间会一直发生碰摩。因此在此状态下,限幅减振器虽然能减小传动轴的共振幅值,但影响了传动轴工作转速下的稳定运行。限幅减振器已经不适用于对该不平衡量的传动轴进行跨临界减振。
3. 2. 4 限位状态响应
若不平衡量再进一步增大,此时传动轴的响应对应传动轴发生故障(如连接件掉落、遭受弹击损伤等)时的響应。在这种大不平衡量情况下,限幅减振器将工作在限位状态,主要利用碰摩环与底座之间的二次限位碰撞实现对传动轴的限位保护。图 8 给出了限幅减振器处于限位状态时的传动轴典型响应结果,其中传动轴的不平衡量设置为 8 kg·mm。蓝色曲线为限幅减振器产生限位作用时的传动轴响应结果,紫色曲线为限幅减振器不具有二次碰撞限位功能只利用传动轴与碰摩环之间的单间隙碰撞及干摩擦减振的响应结果。
在此不平衡量下,未安装限幅减振器时传动轴共振幅值高达 66.713 mm(图 8 中未给出),单间隙碰撞及干摩擦作用下共振幅值为 20.178 mm(图 8 中紫色曲线),幅值减小了 70%,但绝对幅值依旧较大。若进一步引入二次限位碰撞,传动轴的幅值将进一步限制到 7.2416 mm(图 8 中蓝色曲线),相比于单间隙碰撞及干摩擦作用下幅值减小了 64%。由此可见,当传动轴的不平衡量增大到一定值后,仅利用传动轴与碰摩环之间的单间隙碰撞及干摩擦减振,传动轴的振幅依然很大,这时利用碰摩环与底座之间的二次限位碰撞,可以将传动轴的振幅限制在很小的范围内。因此当传动轴处于故障工况时,限幅减振器可以利用碰摩环与底座之间的限位碰撞对振幅较大的传动轴起到一定的保护作用,这对于尾传动系统在故障工况下依旧能运行一定时间以安全迫降至关重要。
4 限幅减振器参数对工作效果的影响规律
根据上文的分析结果可知,在减振状态下,限幅减振器主要是通过传动轴与碰摩环之间的碰撞以及碰摩环与底座之间的干摩擦两种机制实现对传动轴的减振作用。因此分别研究了与这两种机制密切相关的三个参数对减振效果的影响,分别为传动轴与碰摩环之间间隙 δ1、碰撞刚度 k 1 及临界摩擦力 μFn。在限位状态下,限幅减振器主要通过碰摩环与底座之间的二次碰撞实现限位作用,因此研究了碰摩环与底座碰撞刚度 k 2 对减振器限位效果的影响。
4. 1 传动轴与碰摩环间隙对减振效果的影响
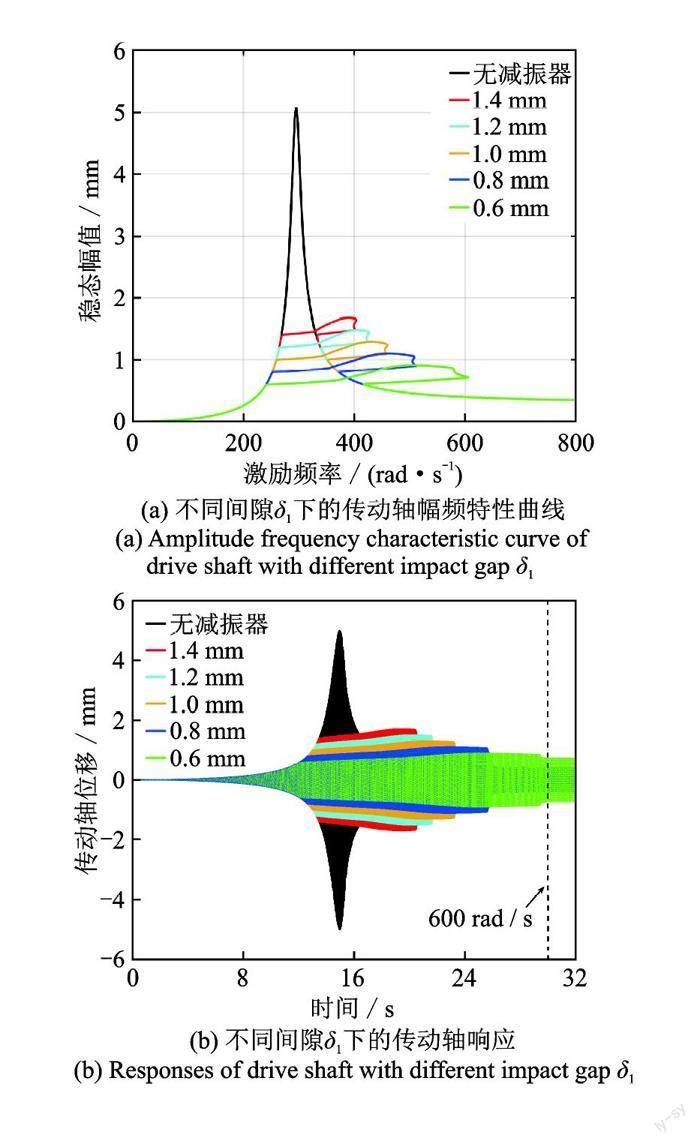
为了研究传动轴与碰摩环之间间隙 δ1 对限幅减振器减振效果的影响,分别给出不同 δ1 下传动轴振动的幅频特性曲线、跨临界转速过程的位移响应以及共振幅值随 δ1 的变化曲线,如图 9 所示。作为参考,图 9(a)和(b)中黑色曲線为未安装限幅减振器时传动轴的幅频特性及瞬态响应结果。
从图 9 中可以看出,随着 δ1 的减小,传动轴的共振幅值逐渐减小,共振频率逐渐增大。出现这种现象主要是因为 δ1 的减小使传动轴与碰摩环之间碰撞深度增加,传动轴的附加刚度增大,从而使传动轴共振幅值减小,共振频率增大。但 δ1 过小会使限幅减振器进入异常减振状态,图 9(c)中虚线部分即表示在该 δ1 下,限幅减振器将处于异常减振状态。此外,由图 9(c)可知,在正常工作范围内,传动轴共振幅值与间隙 δ1 近似满足线性关系,δ1 每减小 0.1 mm,共振幅值降低约 0.1 mm。在设计限幅减振器时,应使传动轴与限幅减振器之间间隙尽可能小,但同时应留有一定安全裕度以避免间隙过小影响传动轴正常运转。
4. 2 传动轴与碰摩环碰撞刚度对减振效果的影响
为了分析传动轴与碰摩环之间的碰撞刚度 k 1 对限幅减振器减振效果的影响,分别给出了不同 k 1 下传动轴振动的幅频特性曲线、跨临界转速过程的位移响应以及共振幅值随 k 1 的变化曲线,如图 10 所示。作为参考,图 10(a)和(b)中黑色曲线为未安装限幅减振器时传动轴的幅频特性及瞬态响应结果。
从图 10 中可以看出,随着 k 1 的增加,传动轴的共振频率变化不大,共振幅值整体呈现出减小的趋势,但在 k 1 从 5000 kN/m 变化到 6000 kN/m 时略有增加。传动轴的共振幅值随 k 1 的增加而减小是因为k 1 越大,碰摩环越容易克服最大静摩擦力而运动,从而为系统引入更多的干摩擦阻尼。共振幅值在 k 1 从5000 kN/m 变化到 6000 kN/m 时略有增加是因为在此范围内,传动轴与碰摩环之间的“侵入分离”过程由两次过渡到多次,而多次“侵入分离”过程的产生不利于传动轴的减振,使振幅增加。此外,根据图10(c)可知,当 k 1 小于 4000 kN/m 时,传动轴共振峰值会随着 k 1 的增大迅速降低,对 k 1 的变化比较敏感,从设计角度讲,应当避免在此区间取值;当 k 1 大于4000 kN/m 时,共振峰值随 k1的变化相对比较缓慢。
图 11 给出了两种典型刚度下传动轴与碰摩环之间侵入位移随时间的演化过程。在单次碰撞过程中,传动轴与碰摩环之间的侵入位移会发生明显的振荡,即产生“侵入分离”的过程。当 k 1 小于 5000kN/m 时,在单次碰撞过程中,传动轴与碰摩环发生两次“侵入分离”过程,而当 k 1 大于 5000 kN/m 时,会发生多次“侵入分离”过程。这种多次“侵入分离”会减缓干摩擦作用的引入,对减振造成不利影响。此外,在图 11 所示的“侵入分离”过程中,侵入位移未减到零,即传动轴与碰摩环并未彻底分离。而在仿真过程中发现,改变碰撞刚度或碰撞阻尼,可能会导致在“侵入分离”过程中侵入位移多次减为零,即传动轴单向运动过程中与碰摩环发生多次碰撞。此时碰撞对减振的不利影响会更大。
4. 3 临界摩擦力对减振效果的影响
为了研究临界摩擦力 μFn 大小对限幅减振器减振效果的影响,给出了不同 μFn 下传动轴的幅频特性曲线、跨临界转速过程的位移响应以及共振幅值随临界摩擦力的变化曲线,如图 12 所示。作为参考,图 12(a)和(b)中黑色曲线为限幅减振器无作用时传动轴的幅频特性及瞬态响应结果。
从图 12 中可知,随着 μFn 的增大,传动轴的共振频率逐渐增大,共振幅值先减小后增大,存在最优的临界摩擦力值使传动轴共振幅值最小。当 μFn 增大到一定值后,限幅减振器会进入异常减振状态,μFn进一步增大,碰摩环发生黏滞,传动轴的共振幅值不随 μFn 增大而变化。图 12(c)中虚线部分即表示在该临界摩擦力下,限幅减振器处于异常减振或黏滞状态。此外,由图 12(c)可知,当 μFn 小于 500 N 时,共振峰值随 μFn 的增大迅速减小,对 μFn 的变化比较敏感;而当 μFn 大于 500 N 时,共振峰值的变化相对缓慢。由于临界摩擦力在使用过程中会不可避免地发生改变,从设计的角度,一般会希望在最优临界摩擦力附近共振峰值对 μFn 的变化不敏感。
由于限幅减振器在减振工作状态下主要是依靠干摩擦实现对传动轴振动能量的消耗,因此临界摩擦力大小是影响限幅减振器减振效果的一个重要因素。为了进一步研究临界摩擦力 μFn 对减振效果的影响规律,给出了在不同的不平衡量、间隙 δ1 及碰撞刚度 k 1 的情况下传动轴的共振幅值随临界摩擦力的变化曲线,如图 13 所示。图中虚线部分均表示在该参数下,限幅减振器处于异常减振状态或黏滞状态,黑色箭头表示传动轴共振幅值最优点的变化趋势。
从图 13 中可以看出,在不同的传动轴不平衡量、间隙 δ1 及碰撞刚度 k 1 下,随着临界摩擦力 μFn 的增大,传动轴的共振幅值均存在最小值。但最优临界摩擦力值随三者的变化规律有所不同。最优临界摩擦力值随不平衡量及 k 1 的增大而逐渐增大,但不随 δ1 的变化而变化。此外,从图 13 中也可以看出使限幅减振器进入异常减振状态或黏滞状态的临界摩擦力值随三者的变化规律:不平衡量越大,使限幅减振器进入异常减振或黏滞状态的临界摩擦力值越小;δ1 和 k 1 越大,进入异常减振或黏滞状态的临界摩擦力值越大。
4. 4 碰摩环与底座碰撞刚度对限位效果的影响
为了研究碰摩环与底座碰撞刚度 k 2 对限幅减振器限位效果的影响,给出了不同碰撞刚度 k 2 下传动轴的位移动态响应结果以及限位幅值随 k 2 的变化曲线,如图 14 所示。从图 14 中可以看出,随着 k 2 的增大,传动轴的振幅被限制在更小的范围内。并且当k 2 小于 5000 kN/m 时,限位幅值对碰撞刚度的变化比较敏感;当 k 2 大于 5000 kN/m 时,限位幅值对碰撞刚度的变化相对比较缓慢。
但更大的刚度也意味着会产生更大的冲击力,碰撞刚度 k 2 对底座受力的影响如图 15 所示。从图15 中可以看出,随碰摩环与底座之间碰撞刚度 k 2 的增大,底座受力最大值先急剧增大后缓慢减小再缓慢增大。k 2 在 1000 kN/m 附近时,由于系统共振会产生一个冲击力共振峰值。图 14,15 表明,增大碰摩環与底座的碰撞刚度虽然可以使传动轴的振幅减小,但同时也会产生更大的冲击力,并且需注意避开共振导致的冲击力峰值。
5 试验验证
为了验证上述理论模型的正确性,设计和加工了限幅减振器试验件,并在单跨轴系试验台上进行了限幅减振器减振试验。
单跨轴系试验台如图 16 所示,该试验台由电机、联轴器、支承、偏心盘及传动轴等组成。传动轴外径 12 mm,限幅减振器试验件安装在传动轴中部,其结构如图 16(c)所示。采用激光位移传感器测量传动轴中部振动位移。为了验证传动轴与限幅减振器之间间隙及临界摩擦力对振幅的影响,设计碰摩环的内径为 13.2,14.4 及 15.6 mm,使传动轴与碰摩环的间隙为 0.6,1.2 及 1.8 mm;设计碰摩环与螺栓之间的间隙为 2 mm,以保证碰摩环与螺栓之间不发生碰撞;同时在实验中保持摩擦片不变,可以通过调节弹簧的预紧力控制临界摩擦力的大小,本实验调节弹簧的压缩量为 5,10,15,20 及 22 mm。实验中,分别在不同的间隙下调节弹簧压缩量,控制传动轴经 30 s 匀加速到 2300 r/min,得到不同初始间隙δ1 及临界摩擦力下传动轴的跨临界横向振动响应,每组实验重复 3 次。
图 17 给出了间隙 δ1 为 1.8 mm 及弹簧压缩量为10 mm 时传动轴的响应结果。从图 17 中可以看出,此时减振器工作在正常减振状态,传动轴振动波形与上述数值仿真结果相符,碰摩环经历了从黏滞到滑动(图中 a~b 和 b~c 阶段)的运动过程,符合理论分析的结果。
图 18(a)给出了弹簧压缩量为 15 mm 时,传动轴的共振幅值随间隙的变化规律。图 18(b)给出了间隙为 1.2 mm 时,传动轴共振幅值随弹簧压缩量的变化规律。传动轴在不同的间隙下随临界摩擦力的变化结果如图 18(c)所示。可以看出,传动轴的共振幅值随间隙的变化基本呈现出线性的变化规律,随着弹簧压缩量的增加先减小后增大。实验得到的参数影响规律与仿真结果相符,验证了本文理论模型的正确性。
6 结 论
本文通过对传动轴与限幅减振器系统进行非线性动力学建模与仿真,得到以下几点结论:
(1)随着传动轴不平衡量的变化,限幅减振器存在四种工作状态,即无作用状态、正常减振状态、异常减振状态及限位状态。限幅减振器主要工作在减振状态,利用传动轴与碰摩环的碰撞及干摩擦进行减振;通过引入二次碰撞,可以对故障工况下的传动轴起到一定的限位保护作用。
(2)在减振状态下,传动轴共振幅值随传动轴与碰摩环之间间隙的减小而减小,随两者之间碰撞刚度的增大总体呈现减小的趋势,随滑动摩擦力的增大先减小后增大。并且,最优滑动摩擦力值会随传动轴不平衡量及传动轴与碰摩环碰撞刚度的变化而变化,而受传动轴与碰摩环之间间隙影响较小。在限位状态下,碰摩环与底座之间的碰撞刚度越大,传动轴的振幅越小,但同时也意味着底座可能受到更大的冲击力。
在今后的研究工作中,拟进一步考虑传动轴的涡动影响,建立二维平面以及三维空间的传动轴与限幅减振器的非线性动力学模型,彻底厘清限幅减振器的工作机理以及参数对减振器减振性能的影响规律。
参考文献:
[1] 佘亦曦,康丽霞,唐朋 . 直升机传动系统的现状与发展研究[J]. 航空科学技术,2021,32(1):7882.She Yixi, Kang Lixia, Tang Peng. Development status and future trend of helicopter transmission system[J].Aeronautical Science & Technology,2021,32(1):78-82.
[2] 梅庆 . 直升机传动轴系的动力学设计[J]. 机械传动,2005,29(5):19-22.Mei Qing. Dynamics design of helicopter drive shafts[J]. Journal of Mechanical Transmission, 2005, 29(5):19-22.
[3] 康丽霞,曹义华,梅庆 . 直升机传动系统花键连接轴的 动 力 失 稳[J]. 北 京 航 空 航 天 大 学 学 报 ,2010,36(6):645-649.Kang Lixia, Cao Yihua, Mei Qing. Dynamic instability of helicopter transmission rotating shafts with spline coupling[J]. Journal of Beijing University of Aeronautics and Astronautics,2010,36(6):645-649.
[4] 谭武中,王祁波 . 直升机传动系统装机振动特性综述[J]. 科学技术创新,2019(2):1-3.Tan Wuzhong, Wang Qibo. An overview on vibration characteristics of helicopter transmission system installed[J]. Scientific and Technological Innovation,2019(2):1-3.
[5] 王锡龙 . 粘弹性减振器对直升机传动轴系动力学特性的影响研究[D]. 南京:南京航空航天大学,2012:3.Wang Xilong. Research on the effects of viscoelastic damper to the dynamics of helicopter drive shaft system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics,2012:3.
[6] zaydn O, Cigeroglu E. Effect of Dry Friction Damping on the Dynamic Response of Helicopter Tail Shaft[M]. Rotating Machinery, Hybrid Test Methods, Vibro-Acoustics & Laser Vibrometry, Volume 8. Springer, Cham,2017:23-30.
[7] zaydn O. Vibration reduction of helicopter tail shaft by using dry friction dampers[D]. Ankara: Middle East Technical University,2017:1-85.
[8] Dygado Z, Perkowski W. Research on dynamics of a supercritical propulsion shaft equipped with a dry friction damper[J]. Aircraft Engineering and Aerospace Technology,2002,74(5):447-454.
[9] Huang Zhonghe, Tan Jianping, Liu Chuliang, et al.Dynamic characteristics of a segmented supercritical driveline with flexible couplings and dry friction dampers[J]. Symmetry,2021,13(2):281.
[10] Hetherington P L, Kraus R F, Darlow M S. Demonstration of a supercritical composite helicopter power transmission shaft[J]. Journal of the American Helicopter Society,1990,35(1):23-28.
[11] Spears S. Design and certification of the model 429 supercritical tail rotor driveshaft[C]. American Helicopter Society Annual Forum 64. Montreal, Canada,2008:2452-2457.
[12] 廖明夫 . 航空发动机转子动力学[M]. 西安:西北工业大学出版社,2015:13-14.Liao Mingfu. Aeroengine Rotor Dynamics[M]. Xi'an:Northwestern Polytechnical University Press, 2015:13-14.
[13] 江俊,陈艳华 . 转子与定子碰摩的非线性动力学研究[J]. 力学进展,2013,43(1):132-148.Jiang Jun, Chen Yanhua. Advances in the research on nonlinear phenomena in rotor/stator rubbing systems[J]. Advances in Mechanics,2013,43(1):132-148.
[14] Hunt K H, Crossley F R E. Coefficient of restitution interpreted as damping in vibroimpact[J]. Journal of Applied Mechanics,1975,42(2):440-445.
[15] Pennestri E, Rossi V, Salvini P, et al. Review and comparison of dry friction force models[J]. Nonlinear Dynamics,2016,83(4):1785-1801.
[16] Shampine L F, Reichelt M W, Kierzenka J A. Solving index-1 DAEs in MATLAB and Simulink[J]. SIAM Review,1999,41(3):538-552.
[17] Krack M, Gross J. Harmonic Balance for Nonlinear Vibration Problems[M]. Cham: Springer International Publishing,2019.
[18] Woiwode L, Balaji N N, Tubita F, et al. Comparison of two algorithms for harmonic balance and path continuation[J]. Mechanical Systems and Signal Processing,2020,136:106503.
[19] 孙传宗 . 航空发动机双转子系统高精度动力学建模与碰摩响应研究[D]. 哈尔滨:哈尔滨工业大学,2017:13-16.
Sun Chuanzong. Accurate dynamical modelling for dual rotor aero-engine system and its response induced by rub impact[D]. Harbin: Harbin Institute of Technology,2017:13-16.
[20] 宋興武 . 直升机尾传动轴系设计[D]. 哈尔滨:哈尔滨工程大学,2007:43-66.
Song Xingwu. Designing of tail transmission shafting for the copter[D]. Harbin: Harbin Engineering University,2007:43-66.

