高速与高阶的超奈奎斯特比较

摘要：超奈奎斯特（Faster-than-Nyquist， FTN）可以提高通信系统的频谱效率（Spectrum Efficiency， SE）。除了较小时间压缩因子（Time Packing Factor， TPF）和星座点数M的高速 FTN 之外，较大TPF和M的高阶FTN也可以增加SE。在相同SE的条件下，本文采用外信息转移（Extrinsic Information Transfer， EXIT）图分析和数值仿真等方法来比较高速和高阶FTN。 针对高速和高阶FTN，本文采用基于EXIT 图的骨干粒子群优化（Bare-Bones Particle Swarm Optimization， BB-PSO）算法来优化两者的信道编码，获得高速和高阶FTN的最优性能。结果表明：与高速 FTN 相比，高阶 FTN 在性能和复杂度方面更有优势。

关键词：高速；高阶；超奈奎斯特；外信息转移图；骨干粒子群优化算法

一、介绍

频谱效率（Spectrum Efficiency，SE）是传输系统的关键性能指标。与奈奎斯特系统相比，超奈奎斯特 （Faster-than-Nyquist， FTN） 能以更快的符号速率传输数据从而增加SE。FTN是未来毫米波和太赫兹通信中的一项潜在关键技术。对于 FTN，符号周期 Ts＝τT，其中τ是时间压缩因子（Time Packing Factor，TPF），T是τ=1时的参考符号周期（一般为奈奎斯特符号周期）。 因此，对于FTN系统，除了增加星座点数M，减小TPF也可以增加SE。随着TPF趋于零，FTN的二进制信息速率收敛到高斯容量限[1]。在相同SE条件下，小TPF和M 引导高速FTN，大TPF和M引导高阶FTN。高速和高阶FTN都随着复杂度的增加而提高了SE。但是，目前还鲜有文献在相同SE的前提下对高阶和高速FTN的性能和复杂度进行比较。

本文分别优化了高阶和高速FTN的信道编码，在两者都匹配最优信道编码的前提下解决上述开放问题。本文考虑两种类型的信道编码，卷积码（Convolutional Code， CC）和低密度奇偶校验（Low Density Parity Check， LDPC）码。文献[2]中的高阶FTN没有优化相应的信道编码。Yu等人在文献[3]中首次研究了基于LDPC码的高阶FTN。然而，由于信道响应的截断，高阶FTN具有次优性能。Bedeer等在文献[4]中研究了高阶FTN，但是没有优化对应的信道编码。

本文采用基于外信息传输（Extrinsic Information Transfer， EXIT）图的骨干粒子群优化（Bare-Bones Particle Swarm Optimization， BB-PSO）算法，分别优化高速FTN和高阶FTN的信道编码。BB-PSO算法是人工智能（Artificial Intelligence， AI）优化算法之一，它是一种优化非线性函数的智能算法。最后，基于信道编码优化，本文在相同SE的条件下比较高阶FTN和高速FTN的性能和复杂性。

二、系统模型

高速和高阶FTN的系统模型如图1所示。信道编码器的码率为r。对于高速 FTN，比特交织器的输出d馈送到Doping编码器。Doping编码器是一个码率为1的递归卷积码，用于消除错误平层。对于高阶 FTN，发射器不包含Doping编码器。FTN调制器的成型脉冲为h（t）。成型脉冲一般为滚降因子β的T-正交根升余弦（root Raised-Cosine， rRC）。FTN 信号可表示为

（1）

其中。h（t）具有单位能量 ， 其双边带带宽 。

FTN信号s（t）通过AWGN信道传输，接收信号为 r（t）。在接收机中，r（t）对应的采样信号r通过前端滤波器hr[5]。接收机采用基于max-log-MAP的低复杂度FTN均衡器，该均衡器采用Ungerboeck模型和信道缩短（Channel Shortening， CS）方法[5]。CS 算法计算前端滤波器hr和目标响应gr。对数似然比（Log Likelihood Ratio， LLR）值在FTN 均衡器和信道译码器之间传递。在很小BER条件下（例如10-5），編码调制（Coded Modulation， CM）-FTN的SE为

（2）

其中m=log2M，TsW为每个FTN符号占用的时频资源。

三、FTN 的信道编码优化

本文使用BB-PSO来找到CC的最优生成多项式和LDPC的最优度分布[6]，该算法的关键是确定适应度函数f和粒子位置Ψ，BB-PSO的拓扑为环形结构。

（一）卷积码优化

基于CC的FTN系统在均衡器（内译码器）和CC解码器（外译码器）之间的进行迭代。基于CC的FTN系统的内译码器的EXIT [7]特性定义

（3）

其中是比特流d（或v）与先验LLRs（或）之间的互信息；是比特流d（或v）与外LLRs （或）之间的互信息；外译码器的EXIT特性与Eb / N0无关

（4）

其中是编码比特c与先验LLR值L额之间的互信息；是编码比特c和外LLR值L之间的互信息。

CC的生成多项式决定了CC译码器的EXIT特性。生成多项式优化描述为

（5）

其中CC的生成多项式为有寄存器，则适应度函数为

（6）

其中表征生成多项式对收敛隧道的影响

（7）

表示内译码器在（5）中 EXIT 特征， 是在（6）中的反函数，。

码率为1/、个寄存器的CC有个生成多项式。遍历方法的复杂性太高。是生成多项式的非线性函数。本文采用BB-PSO算法对生成多项式进行优化。为BB-PSO的粒子位置，为适应度函数。

（二）LDPC码优化

FTN的LDPC码优化分为三个步骤： （1）寻找好的度分布；（2）构造好的基矩阵；（3）寻找合适的度矩阵。优化步骤（2）和（3）的主要思想是搜索围长较大的码字，文献[8]中的算法1和3分别对应步骤 （2）和（3）。注意，步骤（1）是优化的关键，度分布是影响基于LDPC的CM-FTN系统整体性能的关键参数。文献[3][8]通过最小化误帧率（Frame Error Rate， FER）来优化度分布。但是基于FER的穷举搜索复杂度非常高。本文利用EXIT图来优化度分布。对于度分布优化，重点关注变量节点译码器（Variable Node Decoder， VND）和校验节点译码器（Check Node Decoder， CND）之间的迭代。将内译码器与VND的级联视为译码器 I，CND视为译码器II。通过匹配译码器I和解码器II的EXIT特性，从而优化度分布。译码器I的EXIT特性为

（8）

其中，变量节点度分布，根据（5），与有关。译码器Ⅱ的EXIT特性为

（9）

其中校验节点的度分布。度分布优化可描述为

（10）

其中度分布，适应度函数为·

（11）

其中，表征对EXIT图收敛通道的影响，

（12）

其中是（11）中的反函数。度分布向量的值是粒子的位置，是适应度函数。

四、结果与讨论

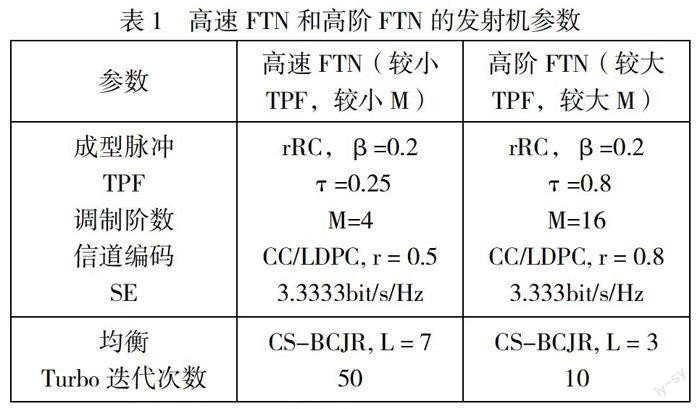
本文分别通过BB-PSO找到了高速FTN和高阶FTN的最优信道编码，最后在相同SE的条件下，比较高速FTN和高阶FTN的性能。 高速FTN和高阶FTN的参数如表1所示。

（一）高速FTN优化结果

1.基于卷积码的优化

对于表1中的高速FTN，BB-PSO算法找到的全局最佳位置，其码长为21000。该码字参考码字为[2]-[2]使用的。与相比，的自由距离或码重更小。基于CC的CM-FTN，自由距离小容易出现错误平层，为此采用doping方法改善错误平层性能。

基于和的高速FTN的BER 性能如图2所示。图中，Nyquist系统与FTN系统的滚降系数相同。Nyquist系统分别使用码率1/2 DVB LDPC、和。BER=10-5时，比较Nyquist系统与FTN系统的性能。FTN（τ=0.25）-NonDoping-CC（7，5）与Nyquist-CC（7，5）相比具有4.9dB 的FTN增益。然而，与Nyquist-DVB LDPC相比，FTN（τ=0.25）-NonDoping-CC（7，5）没有FTN增益。与FTN（τ=0.25）-NonDoping-CC（7，5）相比，FTN（τ=0.25）-NonDoping-CC（3，2）具3.6dB的编码增益。与Nyquist-DVB LDPC相比，FTN（τ=0.25）-NonDoping-CC（3，2）具0.5dB 的编码增益。Nyquist系统的弱码在高速 FTN中可以获得更好的性能。

2.基于LDPC码的优化

对于表1中的高速 FTN，BB-PSO 找到的全局最佳位置，变量节点的平均度分布约为2.06。基矩阵大小为16×32，扩展因子为 661，码长为21152。优化后的码字记为d2.06 LDPC。将rate-1/2 DVB LDPC作为d2.06 LDPC的对比基准。d2.06 LDPC的平均列重小于DVB LDPC，d2.06 LDPC更易出现错误平层。为此，在基于LDPC的高速FTN中引入doping方法，以提高錯误平层性能。基于 d2.06 LDPC 和 DVB LDPC 的高速 FTN 的 BER 性能如图3所示。FTN（τ=0.25）-NonDoping-d2.06 LDPC与 FTN（τ=0.25）-DVB LDPC相比具有近 3.3dB 的码字增益。 DVB LDPC 的平均列重为4.3，d2.06 LDPC 码的平均列重为2.06。可以看出，平均列重较低的LDPC更适合高速FTN。

DVB LDPC 在 Nyquist 和高速 FTN 中的性能：具有相同SE的256QAM-Nyquist-DVB LDPC 相比，FTN（τ=0.25）-DVB LDPC有近5.2dB的性能损失。CC 在Nyquist和高速FTN中的性能：与具有相同SE的256QAM-Nyquist CC（3， 2）相比，具有近 11.5dB 的增益。高速FTN级联不同信道码：FTN（τ=0.25）-NonDoping-d2.06 LDPC与FTN（τ=0.25）-NonDoping-CC（3，2）相比有近2.4dB损失。与256QAM-Nyquist-DVB LDPC相比，FTN（τ=0.25）-NonDoping-CC（3，2）有0.4dB增益。可得出以下结论：①CC更适合高速FTN。与搭配最优LDPC码的高速FTN相比，具有最优CC的高速FTN具有更好的性能。 ②平均列重大的LDPC不适合高速FTN。

对于内码EXIT图，高速FTN均衡器比QAM解调器（Nyquist）更陡。对于高速FTN，CC比LDPC码更适合，如图4所示。QAM解调器的 EXIT图匹配DVB LDPC译码器，如图5所示， QAM解调器的EXIT图不匹配CC译码器，两条EXIT曲线之间总是有交点。EXIT图结果与BER结果一致。从图4和图5可以看出，CC更适合EXIT曲线较陡的内码；LDPC码更适合EXIT曲线平滑的内码。可以看出，CC更匹配高速FTN而不是Nyquist系统。在SE相同的情况下，基于CC的FTN比基于CC的Nyquist具有更好的性能。这也是[2]-[2]的FTN获得高SE收益的原因，进一步可知[2][3]的结论存在局限性。

（二）高速与高阶FTN对比

对于表1中的高阶FTN，BB-PSO算法找到的全局最佳位置，变量节点平均度约为3.6。基矩阵大小为6×30，扩展因子为534，码长为16020，该码字记为d3.6 LDPC。这里将度为3（d3.0 LDPC）的常规LDPC作为d3.6 LDPC 比较基准。d3.6 LDPC的平均列重大于d3.0 LDPC。高阶FTN的EXIT曲线比较平坦，d3.60 LDPC的EXIT图适合高阶FTN。高速FTN和高阶FTN的BER性能如图6所示。

高速FTN和高阶FTN采用最优信道编码。注意，CC的码长比LDPC码更长。与高速FTN （4QAM-FTN（τ=0.25）-Doping-CC（3，2））相比，高阶FTN（16QAM-FTN（τ=0.8）-d3.6 LDPC）有1.9dB增益。对于高阶 FTN，与d3.0 LDPC相比，d3.6 LDPC有0.2dB的编码增益。与具有相同SE的高阶 Nyquist （256QAM-Nyquist-d3.6 LDPC）相比，高阶FTN （16QAM-FTN（τ=0.8）-d3.6 LDPC）有2.3dB的FTN增益。相同SE时，高阶FTN比高速FTN可获更大增益。然而，高速FTN的均衡状态是高阶FTN的两倍；高速FTN的Turbo迭代次数是高阶FTN的5倍。总的来说，与高速FTN相比，高阶FTN在性能和复杂度上都有优势。

五、结束语

在相同SE的条件下，本文分别优化高速FTN和高阶FTN的最优信道编码，最后基于优化结果对高速FTN和高阶FTN的性能进行了比较。優化参数（生成多项式或度分布）与EXIT特性之间为非线性关系。为此，引入基于EXIT图的BB-PSO算法来优化高速FTN和高阶FTN的信道码的生成多项式或度分布。匹配高速FTN的CC和QC LDPC码具有较低的码重。为了提高错误平层性能，高速FTN采用doping方法但是牺牲了收敛性能。高阶FTN无需采用doping方法。与高速FTN（4QAM-FTN（τ=0.25）-Doping-CC（3，2））相比，高阶FTN（16QAM-FTN（τ=0.8）-d3.6 LDPC）具有1.9dB的增益。仿真结果表明优化算法的有效性。与高速FTN相比，高阶FTN在性能和复杂性方面具有优势。从BER性能和复杂度来看，高阶FTN可能是FTN的最有前途的研究方向。

作者单位：车慧 锐捷网络股份有限公司

参  考  文  献

[1] Y. G. Yoo and J. H. Cho， “Asymptotic optimality of binary faster-than-Nyquist signaling，” IEEE Communications Letters， vol. 14， no。 9， pp. 788–790， September 2010。

[2] S. Li， W. Yuan， J. Yuan， B. Bai， D. Wing Kwan Ng， and L. Hanzo， “Time-domain vs frequency-domain equalization for FTN signaling，” IEEE Transactions on Vehicular Technology， vol. 69， no. 8， pp. 9174–9179， Aug 2020.

[3] J. Yu， J. Park， F. Rusek， B. Kudryashov， and I. Bocharova， “High order modulation in faster-than-nyquist signaling communication systems，” in 2014 IEEE 80th Vehicular Technology Conference （VTC2014-Fall）， Sep. 2014， pp. 1–5.

[4] E. Bedeer， M. H. Ahmed， and H. Yanikomeroglu， “Low complexity detection of high-order QAM faster-than-Nyquist signaling，” IEEE Access， vol. 5， pp. 14 579–14 588， 2017.

[5] H. Che and Y. Bai， “Coded modulation faster-than-nyquist transmission with precoder and channel shortening optimization，” China Communications， vol. 18， no. 2， pp. 49–64， Feb 2021.

[6] H. Che， Z. Wu， and W. Kang， “Inner code optimization for high rate faster-than-Nyquist，” in 2019 IEEE Wireless Communications and Networking Conference （WCNC）， April 2019， pp. 1–6.

[7] M. El-Hajjar and L. Hanzo， “EXIT charts for system design and analysis，” IEEE Communications Surveys Tutorials， vol. 16， no。 1， pp. 127–153， First 2014.

[8] I. E. Bocharova， B. D. Kudryashov， and R. Johannesson， “Searching for binary and nonbinary block and convolutional LDPC codes，” IEEE Transactions on Information Theory， vol. 62， no. 1， pp. 163–183， Jan 2016.