基于自适应UKF 算法的虚假数据注入攻击检测研究

伍 虹， 杨 超， 鲁 杰， 徐立立

（1 贵州大学电气工程学院， 贵阳 550025； 2 中国电建贵阳勘测设计研究院， 贵阳 550081）

0 引 言

近年来，随着通信技术以及自动化技术的迅速发展，传统工业设备需面向信息化、网络化发展，与人们日常生活息息相关的电力系统正逐渐发展成一个典型的信息物理系统（Cyber－Physical System，CPS）［1］。 但是由于基础通信网络和信息化设备自身的缺陷以及弊端，电力CPS 在加速构建的同时，电力系统的安全稳定运行也面临新的挑战［2］。

数据采集和监视控制系统（Supervisory Control And Data Acquisition， SCADA）作为电力系统控制中心取得基础量测数据和指令传输控制的关键环节，已成为电力CPS 网络攻击的重要目标，例如：2016年乌克兰国家电网因遭到黑客发起的电力网络攻击而发生区域大面积停电，造成乌克兰西部停电超3小时，波及数以百万计人口的正常生活［3］。 2009 年Liu Yao［4］等首次提出虚假数据注入攻击（False Data Injection Attack， FDIA）定义，指出了静态状态估计中存在的不良数据检测（Bad Data Detection， BDD）原理性漏洞，黑客能在掌握一定电力系统拓扑信息的情况下，通过构造虚假数据攻击向量并注入关键量测装置，以达到既躲过不良数据检测又篡改系统状态估计数值的目的。 作为能量管理系统（Energy Management System， EMS）中的重要组成部分，精准的状态估计对电力CPS 安全控制和经济调度起到关键性作用。 FDIA 作为一种针对电力系统量测数据完整性的新型攻击，由于其强大的破坏性和特殊的隐蔽性，成为近年来电力CPS 中最具威胁性的攻击方式之一［5］。 从攻击者的角度出发，国内外已有大量关于FDIA 模型研究，针对虚假数据注入攻击的检测研究具有实际意义。 如：文献［6］提出一种在未获得完整电网拓扑结构信息情况下，利用状态估计过程进行隐蔽注入攻击的方法；文献［7］认为可以在不需要电网任何拓扑结构和线路信息，黑客攻击者仍然能够发动一种广义上的FDIA；文献［8］提出一种具有多项式的时间复杂度的注入攻击算法，最大程度平衡攻击向量引起的攻击影响和被检验到的概率；文献［9］研究考虑对多个系统状态变量进行注入攻击时，如何最小化攻击向量建模的问题。

本文以静态状态估计—加权最小二乘法（Weighted Least Square， WLS）和自适应无迹卡尔曼滤波（Adaptive Unscented Kalman Filter， AUKF）之间的估计值为基础，以欧几里得距离作为检测指标并设定检测阈值，通过实时比较二者偏差值来判定系统是否遭到虚假数据注入攻击。 以IEEE－14 标准节点系统为例进行仿真，仿真结果表明此方法能够有效检测出虚假数据注入攻击。

1 虚假数据注入攻击

1.1 不良数据检测

在电力系统潮流计算中，量测方程表示为式（1）：

其中，z表示基于SCADA 系统采集得到的量测值（m维列向量）；x表示待估计的状态变量集合（n维列向量，包含节点电压的幅值和相角）；e为量测误差；h（·） 表示量测量和状态变量之间的非线性关系。

由于电力系统的高度非线性，直接对于式（1）应用加权最小二乘法求解状态变量存在计算量大，易发散等问题，因此在实际应用中，往往将其简化为直流模型进行计算，即式（1）简化为式（2）：

其中，H为m×n维雅可比矩阵。

当量测值中存在不良数据，则可以通过最大标准化残差（Largest Normalized Residual， LNR）方法进行不良数据检测，残差r定义为式（3）：

在系统正常运行下，由量测噪声引起的残差r服从自由度为k＝m － n（其中m为量测装置数，n为状态变量），显著性水平为α的分布。 由检测机制可知，当‖r‖2＞τ时，即系统量测数据中存在不良数据；若‖r‖2＜τ，则认为没有不良数据，其中τ为检测阈值。

1.2 虚假数据注入攻击

虚假数据注入攻击是利用不良数据检测缺陷。假设a＝［a1，a2，a3，…，am］T表示为攻击发起者在量测数据中注入的一组攻击向量，则实际量测数据为za＝z＋a；从而状态变量变化为xa＝x＋c，其中c为受攻击后偏差向量，c＝［c1，c2，c3，…，an］T。 此时残差表达式经式（4）和式（5）的推导后，可表示为式（6）：

至此，在不良数据检测机制下，该组攻击向量成功绕过最大标准化残差检验，完成虚假数据注入攻击，成为危害电力系统稳定运行的隐患。

2 UKF 基本原理

无迹卡尔曼滤波（Unscented Kalman Filter，UKF）以卡尔曼滤波为基础，通过引入无迹变换（Unscented Transform， UT）来获取近似非线性变换后的特性。 在动态状态估计中，状态方程和量测方程如式（8）和式（9）：

其中，f（xk） 为状态转移函数；h（xk＋1） 为状态变量和量测值的非线性关系；qk为系统误差；rk＋1为服从均值为0 的加性高斯白噪声的量测误差。

2.1 UT 变换

通过UT 变换获得Sigma 点集，同时为避免采样时的非局部效应和高阶项误差，本文采取对称比例修正法的采样策略。 对于一个n维系统，Sigma 采样策略和均值、方差的权值计算分别如式（10）和式（11）所示：

一共取2n＋1 个Sigma 点，式（10）中的λ＝a2(n＋κ)－n为尺度因子，用于控制预测误差；a为比例修正因子，κ为自由参数，通常取0；β为高阶矩阵信息的权系数，通常取2。

经对称比例修正法采样得到的Sigma 点集{χi}满足式（12）和式（13）：

再一次对Sigma 点集{χi} 进行非线性变换，得到{Yi}，Sigma 点集{Yi} 满足式（14）和式（15）：

无迹卡尔曼滤波通过引入上述UT 变换对Sigma 点进行非线性变换，使得状态变量和协方差能够达到至少二阶以上的精度［10］。

2.2 UKF 预测和更新

2.2.1 状态预测

根据所选采样策略得到的Sigma 点集，进行状态变量x－和协方差阵Px的一步预测，式（16）～式（18）：

2.2.2 量测预测

根据状态预测步得到的状态变量和协方差阵构造新的Sigma 点集，并进行下一步预测，式（19）和式（20）：

2.2.3 滤波更新

根据前两步预测结果计算卡尔曼增益，并对状态变量以及协方差阵进行更新，式（21）～式（25）：

至此完成UKF 的滤波过程。

3 AUKF 动态状态估计

3.1 Holt′s 指数平滑法

由于电力系统的多维非线性，卡尔曼滤波一步预测值中的状态转移方程f（xk） 较难确定。 Holt′s两参数指数平滑法通过过去几个时刻的历史数据进行预测，可以近似得到状态转移函数fHolt，具有计算速度快、不占用系统资源等优势［11］。 其表达式为式（26）～式（28）：

其中，Sk为水平分量；bk为倾斜向量；α和β为平滑系数；取值为［0，1］ 。

Holt′s 两参数平滑法中的α和β选取通过R 语言结合历史数据得到，当α取0.957，β取0.145 时最为合适。

3.2 改进的Sage－Husa 噪声估值器

使用两参数指数平滑法预测的系统噪声未知，有可能随时间发生变换，因此不能简单假设Qk为常数阵。 针对噪声时变问题，本文将基于渐消记忆指数加权法的Sage－Husa 噪声估值器应用于无迹卡尔曼滤波方法中，以此减小未知噪声对模型精度的影响。 改进的Sage－Husa 噪声估值器表达式为式（29）～式（31）：

将Sage－Husa 噪声估值器引入无迹卡尔曼滤波中，实现自适应无迹卡尔曼滤波。

4 FDIAs 检测

传统电力系统在正常运行时，通常使用加权最小二乘法，根据某个时间断面采集得到的量测值来进行静态状态估计，以得到某时刻的状态结果。 而在电力系统遭遇虚假数据注入攻击时，由于WLS 等估计方法的静态特性，被恶意篡改的量测值会使得相应时刻的WLS－SE 远离真实值。 而AUKF 由于Holt＇s 指数平滑法近似得到的转移函数，其状态估计过程具有一定的迟滞性，同时其估计值由预测值和量测值共同决定，由虚假数据注入引起的状态偏移量很小。 因此，可以通过二者状态估计值之间的偏差来检测FDIAs。 本文采用欧几里得距离，即n维空间中两点的真实距离作为检测指标， 式（32）：

为验证所提检测方法，本文采用IEEE14 节点标准系统，用MATLAB 软件及MATPOWER 仿真包获取量测数据，并对系统每五分钟进行一次数据采样，一天二十四小时共计288 次。 基于AUKF 检测虚假数据攻击的仿真结果如下：

（1）系统正常运行时，取某一时间断面T＝ 30时刻，正常运行时IEEE－14 节点电压幅值与相角如图1 所示。 通过仿真计算得到系统正常运行时残差‖r‖2为0.055 8。根据统计学理论，系统冗余度k＝m－n＝14，选择显著性水平为0.05，由卡方分布表得到不良数据检测阈值，此时由量测噪声引起的残差‖r‖2远小于不良数据检测阈值。同时，由欧式检测指标计算得该时刻电压幅值欧氏距离du为0.093 7，电压相角欧氏距离dθ为2.429 8。

图1 正常运行时IEEE－14 节点电压幅值与相角Fig. 1 Voltage amplitude and phase angle of IEEE－14 node during normal operation

（2）注入2 攻击时，取T＝50 时刻，模拟对量测系统注入虚假数据攻击向量［12］。 注入攻击时IEEE－14 节点电压幅值与相角如图2 所示，此时系统运行时残差‖r‖2为0.203 2，注入攻击后的残差远小于不良数据检测阈值τ＝χ214，0.05＝23.685，无法触发不良数据检测机制。 注入攻击前后线路功率对比如图3 所示，此次虚假数据注入攻击造成线路1－2（即1 号量测装置）有功功率和无功功率阻塞，其中有功功率增涨至系统正常运行时的131%，无功功率增涨至系统正常运行时的364%，已成功发起一次虚假数据注入攻击。 由此看见，虚假数据注入攻击在绕过传统不良数据检测的情况下，对电力系统的正常稳定运行已造成严重隐患。 根据欧氏距离检测指标，注入虚假数据攻击向量后，电压幅值欧氏距离du为0.134 6，电压相角欧氏距离dθ为7.249 6。

图2 注入攻击时IEEE－14 节点电压幅值与相角Fig. 2 Voltage amplitude and phase angle of IEEE－14 node during injection attack

图3 注入攻击前后线路功率对比Fig. 3 Comparison of line power before and after injection attack

（3）对全局节点状态变量进行分析，全局节点欧氏距离du与dθ的变化如图4 所示。 采样时刻T ＜50 时，系统正常运行，全局du和dθ保持一个较低水平；当采样时刻T＝50，向系统注入虚假数据攻击向量，在遭遇到FDIA 之后，电压幅值和电压相角欧式距离陡然增涨。 全局残差变化如图5 所示，可以看到在T＝50 时刻前后，全局残差均小于不良数据检测阈值。 在此期间，根据全局节点欧氏距离变化趋势，分别设置电压幅值欧氏距离检测阈值τU＝0. 105和电压相角欧氏距离检测阈值τθ＝3，当du和dθ二者指标超过攻击检测阈值τU和τθ时，即可立即检测出电力系统遭受虚假数据注入攻击；使用均方根误差（Root－Mean Square－Error，RMSE）指标对攻击前后电压幅值和电压相角的精度进行评价。 攻击前后AUKF 性能见表1，在遭受虚假数据注入攻击后，AUKF 仍然能得到较好估计效果。

表1 攻击前后AUKF 性能Tab. 1 AUKF performance before and after attack

图4 全局节点欧式距离变化Fig. 4 Euclidean distance change of global nodes

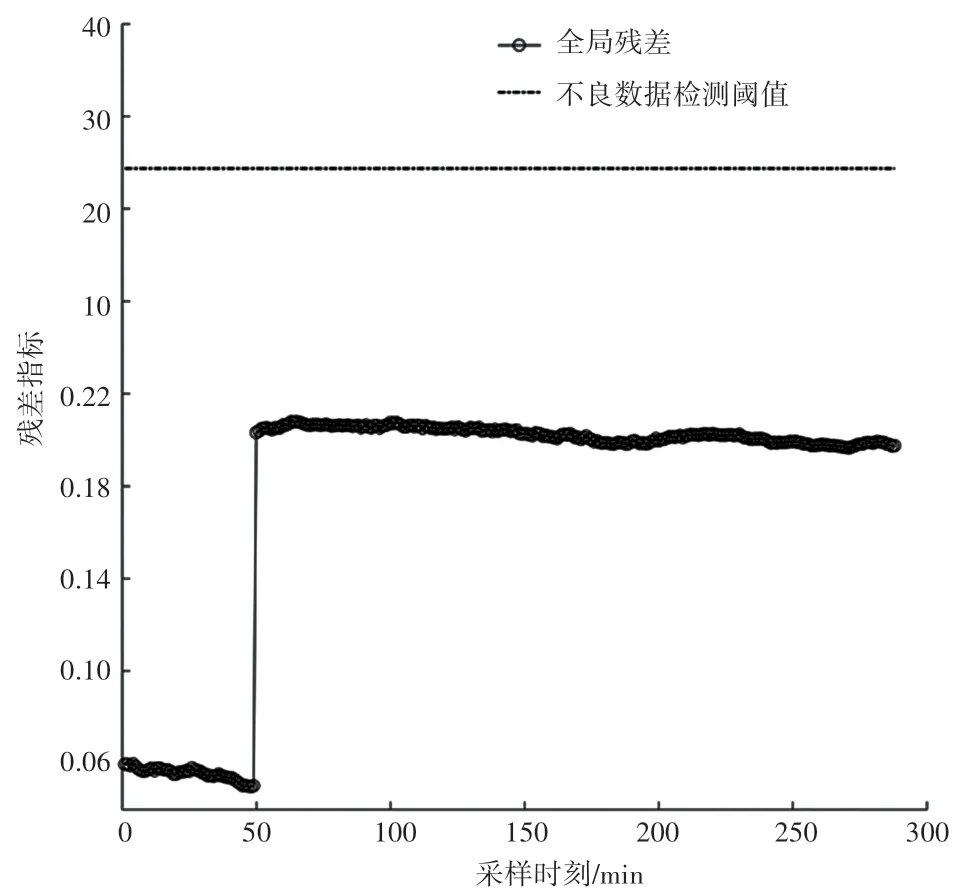
图5 全局残差变化Fig. 5 The global residual

5 结束语

本文提出了一种基于自适应无迹卡尔曼滤波的虚假数据注入攻击检测方法，对电力系统内部进行状态估计，同时利用静态状态估计的实时性和自适应无迹卡尔曼滤波的迟滞性，引入欧几里得距离作为检测系统是否注入虚假数据的指标，并通过设置合理阈值，在IEEE－14 标准节点系统上进行仿真试验。 试验表明：

（1）自适应无迹卡尔曼滤波相比传统静态状态估计具有估计精度高、抗干扰能力强等优点，即使受到虚假数据注入攻击，状态变量变化仍然很小；

（2）自适应无迹卡尔曼滤波能够同时评估当前系统运行状态并预测下一时刻系统的状态；

（3）本文所提方法能够有效、快速地检测出虚假数据的注入，避免电力系统因虚假数据注入攻击做出错误动作。