气体扩散系数法估算水体反硝化速率

李晓寒，严星，夏永秋，颜晓元

（1.中国科学院南京土壤研究所土壤与农业可持续发展国家重点实验室，南京 210008；2.中国科学院大学，北京 100049）

反硝化作用是活性氮最终以惰性氮形式离开土壤、水体等内部生物循环回到大气的最主要的自然途径[1-2]。反硝化过程主要发生在厌氧条件下，在微生物的作用下，硝酸盐被依次转化为亚硝酸盐、NO、N2O，最后以N2的形式返回到大气氮库中。作为反硝化过程的主要产物，N2在空气背景值中的浓度高达78%，要直接测定反硝化脱氮速率，需要方法的精度达到0.1%。准确测定反硝化速率，对于深入理解水体氮循环过程及其氮去除机制具有重要意义。

反硝化速率的估算方法有很多，主要可以分为间接法和直接法。硝酸盐消失法、乙炔抑制法和15N 平衡法等属于间接方法。硝酸盐消失法认为水体中减少的硝酸盐是被反硝化过程所消耗，因此可以基于系统中硝酸盐的减少量来确定反硝化速率，但是由于硝酸盐还会被生物吸收或被沉积物固定，因而这种方法会导致高估反硝化作用。乙炔抑制法是借助乙炔抑制N2O 向N2的转化，通过测定N2O 来间接计算反硝化速率，然而乙炔在抑制N2O向N2转化的同时还会抑制硝化作用，另外乙炔可能会被微生物当作碳源分解利用，从而降低抑制效果，造成反硝化速率被低估[3]。15N 平衡法是通过加入15N 标记的同位素来示踪各种氮作用过程，最后运用差减法计算反硝化作用消耗的氮，一方面人为添加氮源以及同位素的分馏效应会对反硝化过程产生影响，另一方面平衡法因涉及多个过程的测定而存在多个来源的累计误差[4]。

反硝化速率的直接估算方法主要基于N2∶Ar 测定。Ar 是一种惰性气体，在水体中的溶解度主要受温度和盐度控制，其浓度非常稳定。因此，可通过水体中溶解的N2∶Ar 的增量来计算系统中N2的浓度。Kana 等[5]开发的膜进样质谱仪（Membrane inlet mass spectrometer，MIMS），测定N2∶Ar 的误差小于0.03%，因此该方法可以直接测定反硝化作用产生的N2。密闭培养法是将采集的原状沉积物和上覆水在培养柱内进行密闭培养，在培养期间，反硝化产生的N2在培养柱水体中不断累积，因此水中N2浓度随培养时间的增加便反映了系统的反硝化速率。但这种方法需要在原位采集无扰动的沉积物和上覆水带回实验室进行培养，并且在培养、取样以及补水过程中都要求培养体系完全密闭，不能有空气进入。因此该方法野外采集原状沉积物工作量大，实验要求高，培养取样过程也耗时耗力，无法反映水力和环境因子（流速、风速等）对反硝化过程的影响。气体扩散系数法是测定开放水体中溶解的N2∶Ar，根据水-气界面气体扩散系数方程计算出气体扩散系数，进而得到N2的产生速率即反硝化速率。该方法操作简单，不受环境条件限制，而且能反映开放环境如水力和环境因子对反硝化速率的影响。气体扩散法的估算结果取决于水-气界面气体扩散系数的获取。目前，计算水-气界面气体扩散系数的方法有多种，但是选取何种方法确定水-气界面气体扩散系数，方法的可靠性如何，以及方法的不确定性如何，对于这些方面的研究还较少。因此，本研究基于室内培养实验，同步使用密闭培养法和气体扩散系数法，进行扩散系数法可靠性评估与系数确定方法比选，以及扩散系数法参数敏感性分析。本研究对于原位条件下水体反硝化速率的快速、准确估算具有重要意义。

1 材料与方法

1.1 气体扩散系数法

气体在水-气界面的交换通量由气体的扩散速率和气体在水中的实际溶解度与理论溶解度的差值决定，因此N2的扩散通量可由如下公式表示：

式中：FN2指N2在水-气界面的扩散通量，mg·m-2·h-1（以N2计，下同）；kN2指N2的扩散速率，cm·h-1；cwater指水中溶解的N2浓度，mg·L-1；cequal指水-气平衡时理论上水中溶解的N2浓度，mg·L-1，可以根据采样点的水温和盐度计算[6]。

kN2与k600有如下关系：

SCN2=1 970.7-131.45×T+4.139×T2-0.052 106×T3式中：k600是20 ℃下CO2的扩散系数，cm·h-1；SCN2和600分别是淡水中N2和CO2的施密特数，属于无量纲参数，气体的施密特数是关于水体温度（T，℃）的三次函数[7]；n是 施 密 特 系 数，当 风 速 小 于3.6 m·s-1时，n=2/3，否则，n=1/2[8]。目前常用于估算k600的模型主要是kwind-current类型，如表1 所示，即模型中既包含风速又包含水力参数（流速、水深）。不同模型的参数不同，对气体扩散通量的估算也存在一定差异，因此本研究比较并标定了表中的3种气体扩散系数模型。

表1 气体扩散系数模型Table 1 Gas diffusion coefficient model

在u10不易获取的情况下，可以通过水面上方1 m处的风速u1（m·s-1）进行换算[12]。

1.2 密闭培养法

密闭培养法是将无扰动的原状沉积物与上覆水在密闭的培养体系中进行培养。其原理是随着培养时间延长，反硝化的最终产物N2不断累积，短时间内水体中N2浓度线性增加，因此将水中N2的浓度与时间进行线性回归可得到Y=aX+b，其中斜率a即表示水中N2浓度的变化速率，再结合培养柱的横截面积与上覆水体积，即可准确计算出水体的反硝化速率[13]。

1.3 实验设计

1.3.1 开放培养

为了应用气体扩散系数法，需要测定开放体系内上覆水中溶解的N2浓度。在南京市江宁区秦淮河段（31.87°N，118.86°E）采集0~10 cm 表层沉积物，带回实验室后将沉积物充分混合均匀，然后分装到培养柱中（PVC，内径8 cm、外径9 cm、高度27 cm），培养柱底部用橡胶塞密封，每根培养柱中的底泥高度约为10 cm。用KNO3配制浓度为0、1、2、4、6 mg·L-1（以N 计，下同）的硝酸盐溶液，作为培养体系的上覆水，上覆水的深度为15 cm。每个浓度3 个平行，共15 根培养柱放在水浴培养箱中并维持水温恒定。将培养柱敞口静置在培养箱中预培养一天两夜，使培养体系达到平衡状态。培养体系稳定后取第一个水样作为0 h的样品，然后分别在第2、4、6、8小时取样，每次取3个重复水样。

取样时，用移液枪吸取表层的水样转移到顶空瓶（12 mL，Labco Limited，英国）中，使水样在顶空瓶瓶口形成顶空，然后立即拧紧盖子密封。用移液枪取样过程中注意不要吸入空气，将水样转移到顶空瓶的过程中也尽量不要充入空气，以免污染水样。如果所取样品不能在2 h 内测定，则要在顶空瓶注入水样之前用移液枪深入瓶中加入100 μL 饱和ZnCl2溶液，用于抑制微生物活性。

1.3.2 密闭培养

密闭培养所用培养柱尺寸、底泥和上覆水均与开放培养一致，样品在培养桶中预培养一天两夜使培养体系达到平衡状态，每个浓度下设置3 个平行，与开放培养同时在第0、2、4、6、8 小时取样，每次样品取3个重复。不同于开放培养的是，密闭培养需要保证在培养期间柱内无气体交换，因此需要用密封盖将培养柱密封，密封以及取样的过程中也要注意避免柱内产生气泡。

具体培养和取样方法参照李晓波等[13]的方法。

1.3.3 环境理化因子测定

在开始取样前用HQ301 直接测定培养柱中上覆水的pH、水温、盐度等指标，同时取水样用于后续测定NO-3-N、NH+4-N。

沉积物剔除石块等杂物后混匀，并取样测定pH、NO-3-N、NH+4-N、TN 和TC。沉积物风干后过2 mm 孔径筛，按照水土比2.5∶1振荡并静置后测定pH，NO-3-N、NH+4-N 采用2 mol·L-1KCl 浸提沉积物后测定，TN 和TC在沉积物风干研磨过100目筛后测定。

pH 采用pH 计测定，NO-3、NH+4采用流动分析仪测定，TN 和TC 采用CNS 元素分析仪测定。沉积物的部分理化性质见表2。

表2 沉积物的基本理化性质Table 2 Basic physical-chemical properties of the sediment

1.4 水体中溶解N2的测定

水 中 溶解N2的 浓 度 由MIMS（Bay Instruments，Easton，MD，美国）直接测定。MIMS 主要由蠕动泵、恒温水浴、液氮冷阱、四极杆质谱管、信号收集器、计算机系统组成[5]。待测水样沿进样管在蠕动泵的作用下穿过水浴调节装置，经过温度平衡后进入真空系统并与半透膜接触。水样中的部分气体透过半透膜进入四极质谱管，首先在电离装置作用下进行离子化，而后不同质量的离子经过振荡电场分离后进入检测器。蠕动泵可以将水样以稳定的速度输入到进样系统中，恒温水浴可以快速调节低温保存的水样至实际取样时的温度，液氮冷阱可以去除水蒸气、CO2、CH4等低分子有机化合物，以防对待测气体产生干扰。MIMS通过测定水样N2∶Ar来计算水样中N2的浓度，其精度可达到0.03%。水样中N2浓度的计算公式如下：

式中：fC为校正因子；（[N2]/[Ar]）Sa、（[N2]/[Ar]）St分别表示样品、标准水样中N2∶Ar的实测值；（[N2]/[Ar]）E、[Ar]E分别表示标准水样中N2∶Ar、Ar浓度的理论值。

1.5 参数敏感性分析

本研究旨在理解由扩散系数模型估算的N2通量对输入的各环境变量的敏感性。敏感性分析分为局部敏感性分析（Local sensitivity analysis，LSA）和全局敏感性分析（Global sensitivity analysis，GSA），常用于模型参数不确定性分析。LSA 是在保持其他条件不变情况下，改变某个特定参数来进行敏感性分析[14]，而GSA 是同时改变全部参数来研究全局所有因素的影响[15]。在本研究中，应用蒙特卡洛模拟法分别产生水温、盐度、流速、水深、风速5 个参数的随机数，进行LSA。蒙特卡洛模拟法是在每个因子的分布范围内随机取值，从而产生一系列随机数。各因子的分布和变异基于太湖流域多年观测数据。其中，水温数据和气象数据分别来源于中国环境监测总站和国家气象科学数据中心的相关数据库，流速、水深和盐度的数据来源于已发表的相关文献[16-18]。上述5个参数均属于环境变量，可认为其均服从正态分布。以收集到的数据为基础确定了各参数的均值和标准差（表3），随后用蒙特卡洛法进行了1 000次模拟。

表3 蒙特卡洛模拟所需参数的变化范围Table 3 Range of parameters in Monte Carlo analysis

在本研究中，敏感性的统计指标为无偏百分比差异（Unbiased percent difference，UPD，D），具体计算方法如下：

式中：N为模拟次数；xi指第i次模拟时模型计算的结果；y指N次模拟计算结果的均值。

1.6 统计方法

本研究中数据分析均使用Excel 进行，绘图使用OriginPro 2022完成。

2 结果与分析

2.1 气体扩散系数法的可靠性

如图1 所示，3 种气体扩散系数模型估算出的水体反硝化速率均与上覆水中NO-3-N 的浓度呈正相关，并且用米氏方程能够很好地拟合反硝化速率与反应底物（NO-3-N）浓度之间的关系（R2=0.994 6，P<0.01），米氏常数为1.42。反硝化作用是反硝化菌在无氧条件下，将NO-3-N 作为电子受体完成呼吸作用以获得能量的过程，属于微生物过程，因此反硝化速率与NO-

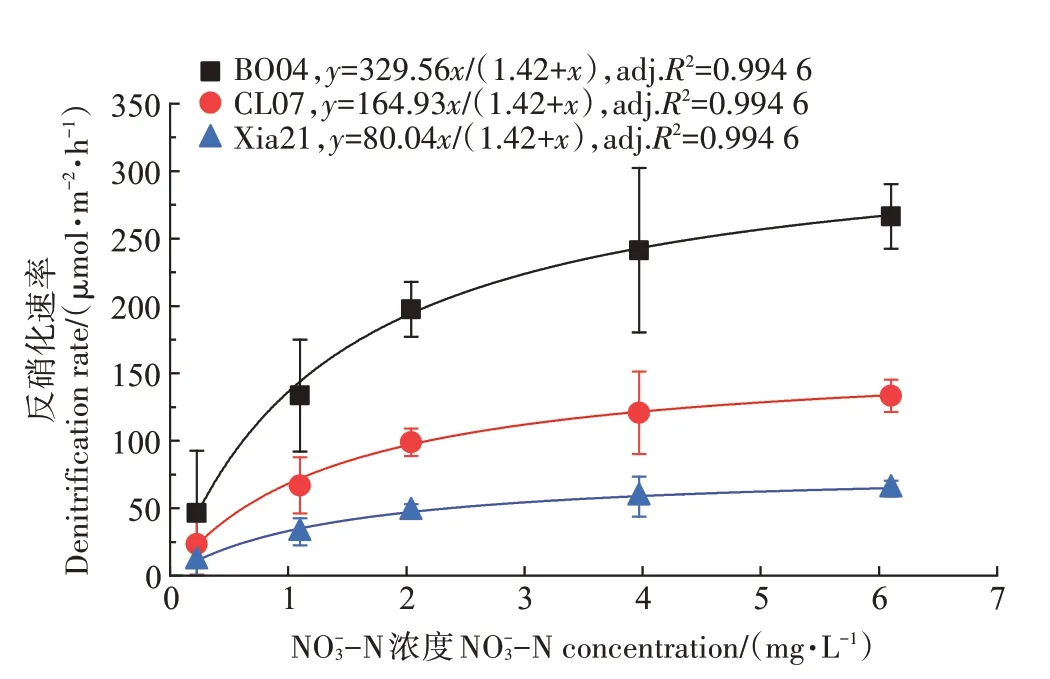
图1 不同气体扩散系数法估算的反硝化速率对NO-3-N浓度的响应关系Figure 1 Relationship between denitrification rates estimated by different gas diffusion coefficient methods and NO-3-N concentration

3-N 浓度之间符合米氏方程的关系。由此也说明气体扩散系数法估算出的反硝化速率能够用于估算水体的反硝化速率。

2.2 结果比较

在气体扩散系数法与密闭培养法的比较中（图2）可以发现，3 种扩散系数法与密闭培养法测定的水体反硝化速率之间均有显著的线性关系（R2=0.776 7，P<0.05），但斜率各不相同，BO04、CL07 和Xia21 的斜率分别为2.44、1.22 和0.59，究其原因是由于模型结构和系数差异造成的。本研究中，3 个模型中风速的系数以及BO04 和Xia21 中水深和流速的系数均是由实测数据拟合分析而来，可认为是经验系数，而CL07中水深和流速的系数是依据热力学原理推导出来的。由此可认为，CL07 属于半经验半机理模型，BO04 与Xia21 属于经验模型。另外，虽然经验模型的系数都是通过统计分析的方法归纳得到，但在分析过程中所用数据集不同，得到的经验系数也会有所不同。也正因为如此，虽然3 种模型纳入的因子一样，但模型结构和系数迥异，导致估算出的结果也存在较大差异。

进一步比较了3 种气体扩散系数模型的反硝化估算结果与密闭培养法的测定结果，如图3 所示，BO04 和CL07 的反硝化速率估算结果分别为46.51~266.42 μmol·m-2·h-1和23.28~133.33 μmol·m-2·h-1，相较于密闭培养法测定结果（24.55~91.20 μmol·m-2·h-1）均较大。而Xia21 估算的反硝化速率（11.30~64.70 μmol·m-2·h-1）相比于密闭培养法测定结果较小。结合图2中3种气体扩散系数法与密闭培养法估算的水体反硝化速率拟合方程的斜率，本研究认为CL07 和Xia21 的估算结果均较为接近密闭培养法的测定结果，但其结果分别偏高和偏低。

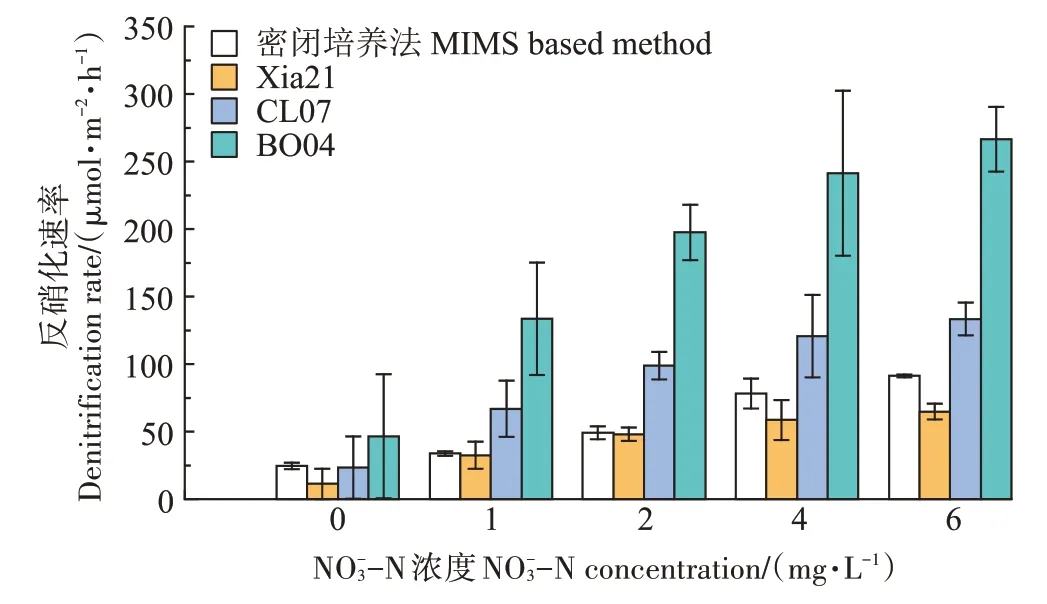
图3 不同扩散模型与密闭培养法估算反硝化速率的结果对比Figure 3 Comparison of denitrification rates estimated by different coefficient diffusion models and MIMS-based method

2.3 气体扩散系数法的参数敏感性分析

本文所选的3 种气体扩散系数模型都纳入了水深、流速和风速3 个参数，同时水温和盐度是决定气体施密特数的参数，因此用扩散系数模型估算反硝化速率的不确定性取决于以上5 个参数的敏感性。以下选择CL07模型进行参数敏感性分析。

参数敏感性分析结果表明，气体扩散系数模型对盐度的变化几乎不敏感（UPD=0.03%），而对风速的变化最为敏感（UPD=12.13%），其次比较敏感的参数是流速和水温，UPD 分别为9.49%和9.42%，对水深也有一定的敏感性，UPD 为6.24%。因此在应用气体扩散系数法估算水体反硝化速率时，风速、流速和水温是3 个最重要的环境因子，其准确性影响着模型的估算精度。水体温度不仅可以通过影响微生物活性从而直接对反硝化速率产生影响，而且水体温度变化会改变N2在水体中的理论溶解度，导致水体中N2的饱和度发生变化，在用扩散系数法估算反硝化速率时会间接影响估算结果。水体的流动一方面有助于硝酸盐底物向底泥补充以促进反硝化作用，另一方面也会使水体溶解氧量增多，破环水体底部的厌氧环境从而抑制反硝化作用，因此水体流速对水体反硝化有着至关重要的作用。风速是影响气体在水-气界面扩散的重要物理因素，是气体扩散系数模型中最重要的环境因子。

3 讨论

在原位状态下，水体反硝化过程受多种因素影响，而目前只有气体扩散系数法能够实现原位直接估算水体的反硝化速率。以往的研究表明，NO-3浓度和水温是水体反硝化的主要控制因子。例如Zhao 等[19]构建的反硝化速率预测模型纳入了水温和NO-3-N 浓度两项参数，模型的解释率达到了85%。一方面，NO-3是反硝化作用的底物，高浓度的NO-3有利于反硝化的发生；另一方面，随着水体温度升高，微生物活性增强，进而促进了反硝化作用。此外，其他的生物化学因子，如溶解氧（DO）[19]、pH 和氧化还原电位（ORP）[20]也会通过影响硝化-反硝化耦合过程来影响水体反硝化速率。近年来，越来越多的研究强调水力因子（如流速、流量、水深、水力停留时间等）在水体反硝化过程中的重要作用。Guo 等[21]通过主成分分析研究发现水力因子（流速、流量）对太湖流域的氮去除贡献率达到14%。Alexander等[22]在墨西哥湾的研究表明，从小河流到大河流，随着河道水深增加，水体的氮去除速率减小。Marce等[23]将已发表文献中的数据进行整理，分析发现水力停留时间可以解释硝酸盐去除的22%~48%。以上研究都表明，原位环境下影响水体反硝化速率的因素多且机制复杂，而密闭培养法不能反映水力和环境因子对反硝化过程的影响，因此估算结果存在很大的不确定性。气体扩散系数法则很好地弥补了这一缺陷，通过在原位直接估算水体的反硝化速率从而能够更加真实地定量反硝化过程。因此该方法可以在大尺度上高频率地进行水体反硝化速率的估算[24-25]。

但值得注意的是，因为影响气体在水-气界面扩散的因素复杂，所以关于在原位条件下估算气体扩散速率的最佳模型尚未达成共识[26-27]，并且不同扩散系数方程估算出的反硝化速率存在明显差异（图3）。与本研究的结果不同，Yang等[28]比较了10种气体扩散系数方程估算的k600，结果显示CL07 的估算结果约是BO04估算结果的2.5倍，这说明了即使相同的气体扩散系数方程在不同研究条件下估算出的结果也会存在差异。因此在不同情境下应用气体扩散系数法进行反硝化速率的估算时，要根据实地环境条件对模型进行标定，从而选择合适的气体扩散系数方程。

4 结论

BO04、CL07和Xia21 3种气体扩散方程均能很好地表征反硝化速率对硝态氮浓度的响应关系。在本试验条件下，CL07和Xia21的估算结果均接近密闭培养法的测定结果。通过对CL07方程进行参数敏感性分析发现，风速、流速和水温是最为敏感的3 个因子，无偏百分比差异分别达到了12.13%、9.49% 和9.42%。总之，气体扩散系数法估算水体反硝化速率具有较高的准确性和可靠性，为区域尺度原位条件下水体反硝化速率的快速、准确估算提供了方法基础。