投饵机下料及抛洒结构优化设计

姜忠爱 ,于 红，吴俊峰，缪新颖，李鹏鹏

（大连海洋大学1.机械与动力工程学院/2.信息工程学院，辽宁 大连 116023）

水产养殖中机械投饵是主要投饵方式，目前池塘投饵机械化水平约为79.71%[1]。在机械化投喂过程中，控制定量及抛洒加速的机械结构会造成饵料破碎，破碎饵料进入水中容易快速溶解，无法被养殖对象进食，造成饵料浪费及水质污染[2-3]。因此，降低饵料破碎率对节约饵料成本及实现生态化养殖具有重要意义。在解决饵料破碎率方面，有学者研究改进气力输送方法，根据不同的投喂效率及风速，饵料破碎率控制在0.1～1.0%之间[4-5]。但气力输送投饵方式耗能大，定量投饵精度低，不适合池塘及工厂化养殖定量投饵需求。前人采用振动下料方式，可减少饵料破碎，饵料破碎率降至0.1%左右，但受物料特性及称重检测精度影响，定量误差高，工作可靠性较差[6-8]。螺旋推进和旋转叶轮是目前定量投饵常见的下料方式，在工作过程中，机械结构会挤压饵料，造成较高的饵料破碎率，而且饵料抛洒需要通过抛洒盘离心加速完成，进一步加剧饵料破碎，通常整体投饵破碎率在1.5%～3.0%之间[3,9-11]。马迪红[3]采用柔性螺旋送料方式及闭式抛洒盘，饵料破碎率降低50%，但是柔性送料方式一定程度上会影响定量送料精度。针对上述问题，本研究分析下料拨轮叶片型线与饵料受力之间的关系，建立饵料在抛洒盘沟槽中的运动学方程，对机械结构进行优化，以期解决叶片式下料拨轮在定量下料过程中及饵料离心加速过程中造成的破碎问题，降低饵料破碎率。

1 总体结构与工作原理

1.1 总体结构

投饵机械结构由机架、料箱、下料拨轮、电机、抛洒盘等部分组成（图1）。

1.2 工作原理

饵料受重力作用从料箱下料口流入拨轮叶片槽内，下料拨轮在电机带动下旋转实现定量下料，随后饵料颗粒在导流槽的作用下落入抛洒盘，并在抛洒盘的离心加速下抛出，实现投喂。整个过程中，下料拨轮叶片与饵料之间相互作用容易造成饵料破碎，同时，在抛洒盘对饵料的加速抛洒过程中也容易造成饵料破碎。

2 主要运动件优化设计

2.1 下料拨轮优化设计

本投饵机的定量下料方式为定容积拨轮下料，属于旋转叶轮式的一种（图2）。

图2 下料装置Fig.2 Feeding device

饵料受重力作用从料箱下方流出充满拨轮槽，由于饵料密度和轮槽容积是确定的，因此，拨轮旋转一周的下料量可由式(1)计算获得：

其中，m为拨轮每旋转一周的下料量（kg）；ρ为颗粒饵料堆积状态下的密度（kg/m3）；D为拨轮顶圆直径（m）；d为拨轮中心传动孔直径（m）；B为拨轮厚度（m）；V为拨轮体积（m3）。

为减少下料过程中拨轮叶片与定容腔之间相对运动导致饵料破碎，设计拨轮径向方向外形为曲线结构，特别是在拨轮叶片与料箱下料口接触区域，饵料受力如图3所示。其中，F0为饵料颗粒自身重力m0g与其所受上方饵料压力Fp的总和；F1为拨轮表面对饵料的作用力，接触点为B点，方向沿拨轮截面型线的法线方向，与接触点基圆法线方向夹角为β（下料拨轮型线切线方向与基圆切线方向夹角）；F2为饵料颗粒受下料口A点处的作用力。

图3 饵料颗粒受力分析Fig.3 Force analysis of bait particle

当A、B 两点距离小于饵料直径且在饵料质心上方时，饵料颗粒可顺利进入拨轮容腔而不被挤压，若AB 连线在质心下方，则饵料颗粒可被推回料箱。当拨轮型线外表面与进料口之间的距离接近饵料直径时容易产生饵料颗粒卡住并挤碎。取A、B 距离恰为饵料直径这一临界情况进行分析，以A点为基点，饵料静力学力矩分析如下：

要满足饵料能够被退回料箱且不被挤碎，则要求MF1＞，且F1小于饵料的许用破碎力Fσ，即：

式(7)中，L0为下料口开度（m）；de为定容腔腔室直径（m）。

由以上分析可得出，要避免饵料破碎，接触点B处，下料拨轮型线切线方向与基圆切线方向夹角β满足：

从饵料受力分析可知，曲线型叶片型线切线方向与基圆切线方向存在夹角β，对饵料颗粒产生向上的推力作用。当饵料处于下料口底部时，此推力可把即将进入却无法进入定容腔的饵料退回料箱。而直线型叶片β角为0，不存在向上的推力作用，其旋转时产生拨动力，更容易将饵料向已经塞满的定容腔内挤压，造成饵料破裂。此外，在相同转速下，β角越大，定容腔体积变化率越小，更有利于饵料调整姿态退回料箱，而直线型叶片定容腔体积变化率快，饵料在拨轮作用下重新调整姿态时间短，加剧饵料的破碎。

因此，对叶片进行曲线型优化设计可有效减少饵料破碎。β角越大，防破碎效果越好，由式(8)可见，该值大小与饵料质量、饵料受上方饵料压力以及下料口开度成正比；与饵料许用破碎力及定容腔内部直径成反比。对于确定的下料口开度及定容腔大小，结合实际饵料特性，可通过式(8)计算β角最小值，并根据计算结果将传统的直线型拨轮叶片优化为曲线型叶片，以避免饵料破碎。同时，为防止下料口饵料板结、架空造成的壅塞，在拨轮轴上安装一偏心轮（图2中的零件2），偏心轮转动过程中产生敲击效应，有助于消除壅塞，确保下料流畅。

2.2 抛洒盘结构优化设计

饵料从定容腔流出后，顺着导流槽落入抛洒盘，抛洒盘上设计有沟槽，通过抛洒盘的旋转，饵料在沟槽中获得离心加速度，最终沿抛洒盘径向甩出。为减少抛洒过程中抛洒盘对饵料的加速冲击造成的破坏，沟槽采用弧形结构设计，且将饵料从抛洒盘上方中心位置流入，以减少其初始加速度。抛洒盘结构及饵料受力分析如图4所示。

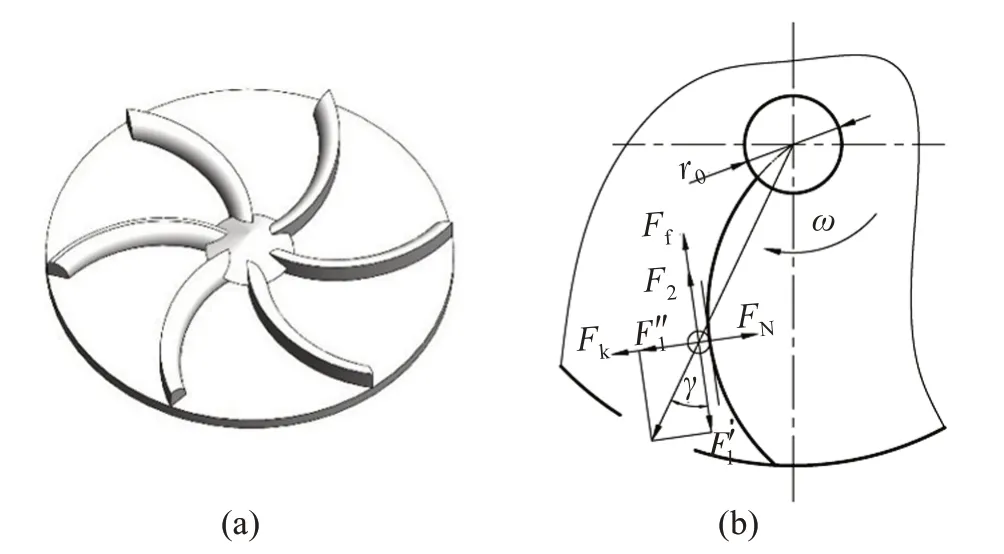
图4 抛洒盘结构(a)及饵料受力分析(b)Fig.4 Structure of throwing plate(a)and force analysis of the bait(b)

将饵料颗粒简化为质点，对其进行运动学建模。颗粒被抛洒盘加速旋转产生的离心力F1为

其中，ω为饵料随抛洒盘旋转的角速度（rad/s）；l为饵料到抛洒盘中心点距离（m）。

饵料颗粒旋转产生的科氏力Fk为

其中，γ为饵料与抛洒盘接触点处沟槽型线切线方向与饵料离心力夹角。

饵料与抛洒盘沟槽接触点压力FN为

饵料与抛洒盘沟槽面摩擦力Ff及饵料自身重力产生的摩擦力F2分别为

其中，μ为饵料与抛洒盘表面之间的摩擦系数。

沿沟槽曲面切线方向，饵料颗粒运动学模型为

其中，r0为饵料首次落入抛洒盘位置距抛洒盘中心之间的距离（m）。

解得饵料颗粒在抛洒盘上，沿沟槽的运动学方程为

从式(10)和(11)可见，对于直线型沟槽，其γ角为0，cosγ=1。将沟槽型线由直线优化为曲线结构，则0 ＜γ＜90°，从而0 ＜cosγ＜1，对于相同的ω，将降低Fk与FN的值，从而实现降低饵料抛洒加速过程的冲击。

式(15)～(20)建立了饵料运动轨迹与硬件结构参数之间的关系，为不同应用场合下抛洒盘的大小、转动速度范围及沟槽型线设计提供科学依据，实现硬件结构柔性设计。在设定抛洒盘转速600 r/min条件下，通过MATLAB 进行饵料运动学规律仿真，获得饵料速度随γ角变化及加速时间的关系（图5）。

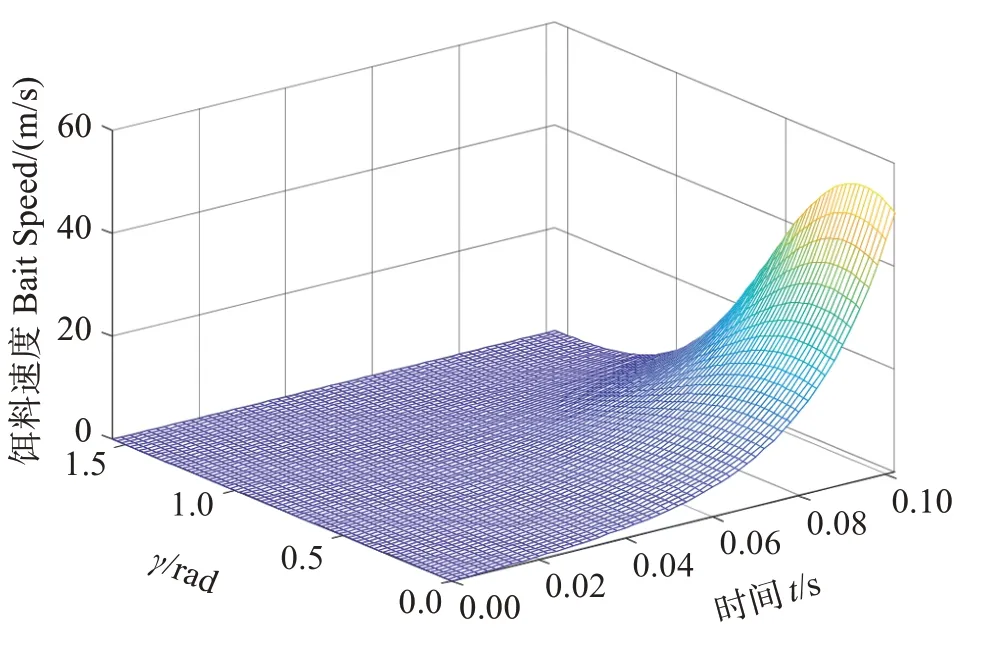
图5 饵料速度随γ角变化及加速时间t的关系Fig.5 The relationship between bait speed and angle γ and acceleration time t

根据养殖投喂需求与实际情况，确定抛洒盘结构参数如下：抛洒盘转速为600 r/min，直径为0.15 m，γ角为30°，沟槽型线方程为y=根据以上结构参数，通过饵料运动学方程计算，饵料会在落入抛洒盘0.053 s 后被加速抛出，此过程饵料的速度和受力情况见图6。

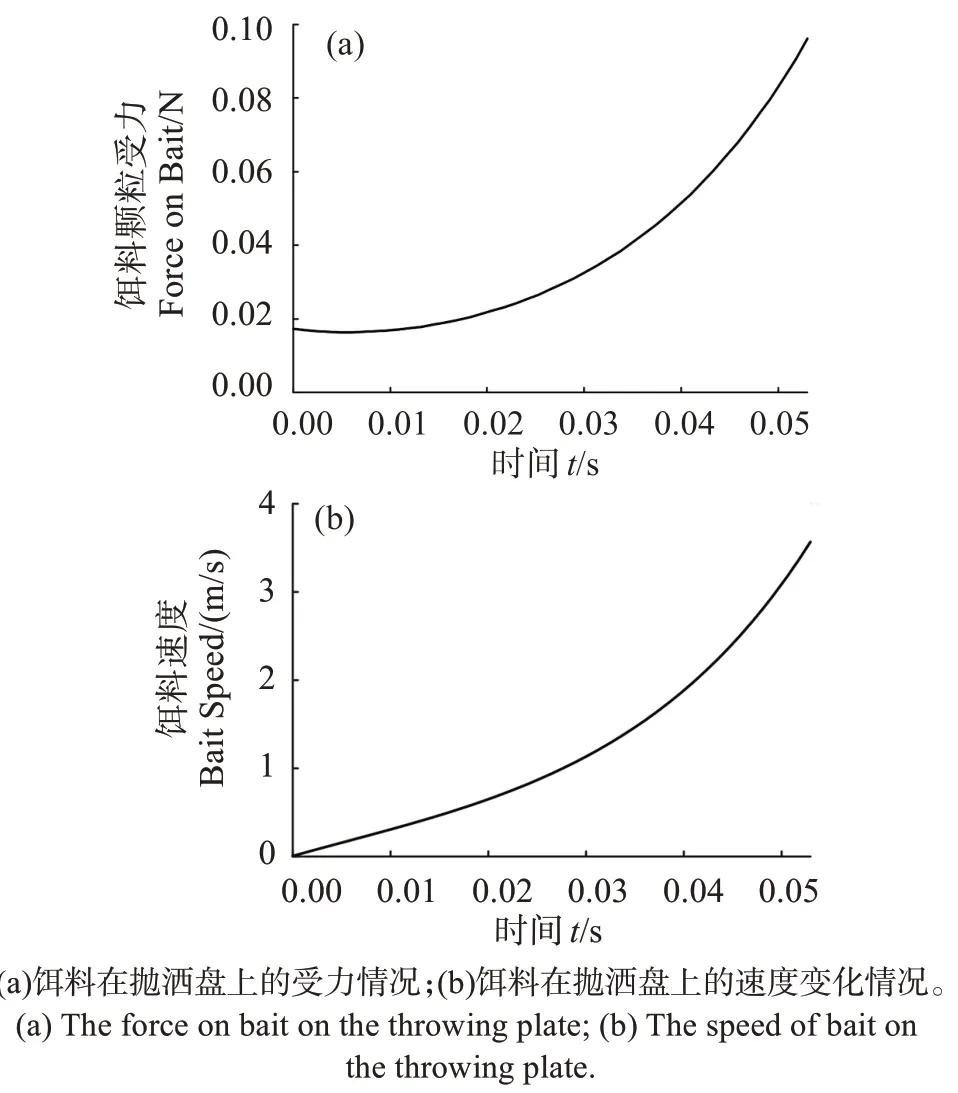
图6 饵料离开抛洒盘前运动学参数变化Fig.6 Ⅴariation of the kinematic parameters before the bait leaves the throwing plate

由图6 可以得出，饵料颗粒在加速抛洒过程中最大受力0.095 N，最大速度3.5 m/s。

2.3 饵料抛洒过程EDEM仿真

为验证抛洒盘结构优化效果，进行直线和曲线沟槽抛洒效果EDEM 仿真，仿真条件设置如下：抛洒盘转速为600 r/min，料粒直径为0.01 m，下料排量1 800 cm3/min，饵料密度1 050 kg/m3，饵料泊松比为0.23，饵料剪切模量为9.74，饵料与料盘动摩擦系数为0.1。

图7 显示沟槽型线优化前后饵料运动轨迹，可见，在直线沟槽条件下饵料轨迹折转剧烈，而曲线沟槽条件下饵料轨迹更平滑，饵料分布更均匀。对应的受力和速度变化情况如图8所示，其数值与图6中运动学建模计算结果基本吻合，最大误差在10%左右，对于在理想状况下建立的数学模型而言，这个误差范围是可以接受的。

图7 饵料运动轨迹仿真结果Fig.7 Simulation result of the bait movement trajectory

图8 直线和曲线沟槽条件下饵料受力(a)与速度(b)曲线Fig.8 Force(a)and velocity(b)curve of the bait under linear and curve grooves throwing condition

从图8(a)中可见，饵料在直线沟槽下受到的冲击力更大，单个饵料受力最大值达0.181 N，而在曲线沟槽条件下饵料最大受力0.109 N，受力减小近40%；从图8(b)速度曲线对比可见，在直线沟槽播撒过程中，速度变化急剧，平均加速度193 m/s2，而在曲线沟槽播撒过程中，饵料速度变化曲线更平稳，平均加速度108 m/s2。这表明，通过优化沟槽型线，饵料受到冲击作用破碎的概率更小，可有效减少饵料破碎率，验证了沟槽优化的效果和必要性。

3 实验与性能分析

根据对下料拨盘与抛洒盘优化设计成果，设计投饵样机（图9），通过实验验证其工作可靠性及实际饵料破碎率。

图9 投饵机样机Fig.9 Prototype of the feeding machine

投饵样机安装在距离地面0.5 m 的平台上，对3种不同规格的饵料进行机械投饵实验，饵料形态如图10所示。

图10 实验采用的三种不同规格的饵料Fig.10 Three kinds of bait with different specifications used in the experiments

对三种饵料按照大小编号分别为1 号、2 号和3号饵料，投饵实验参数设置见表1。

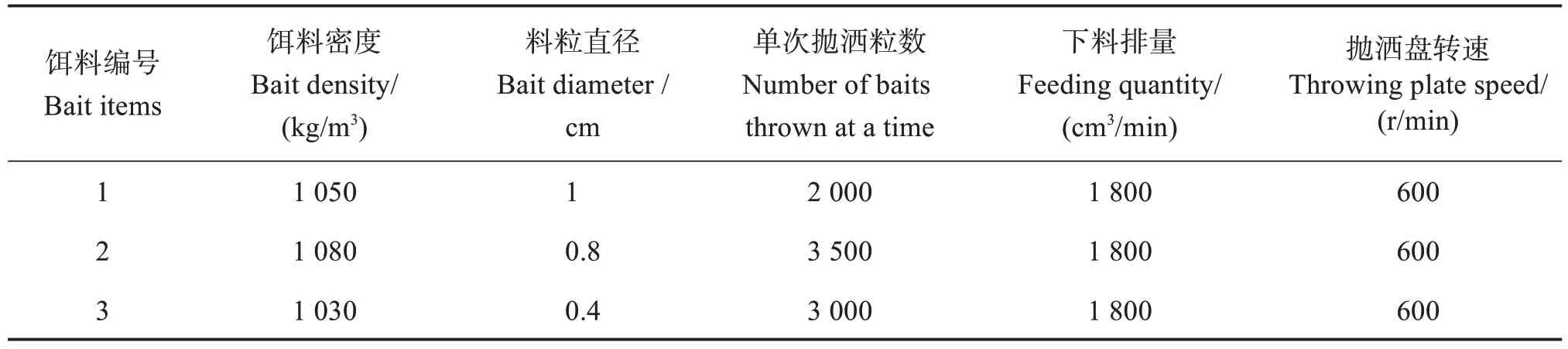
表1 饵料破碎率测试实验参数Table 1 Experimental parameters of bait crushing rate test

播撒实验结束后，修正饵料落地后的滚动误差，测量饵料实际落点均匀分布在半径为1.0～2.5 m 的扇面区域内，该结果与通过运动学方程计算结果及EDEM 仿真基本相同，图11 为1 号饵料EDEM仿真及实验的播撒情况，其他两种饵料也获得的相同的吻合结果。可见，本样机能实现将饵料均匀抛洒在养殖水域中，满足投饵需求，验证了其工作的可靠性。

图11 投饵播撒分布Fig.11 Distribution of baiting

饵料破碎率方面，对三种饵料播撒结束后进行破碎饵料数清点，并对播撒前后饵料颗粒进行称重，以确定下料过程中由于饵料表面不规则边缘磨损形成的雾状粉料比例，这一部分是评价饵料破碎率的重要参数。针对三种不同饵料分别进行四次投饵的实验数据（表2），其饵料破碎率包含挤压破裂的饵料及形成雾状粉料后的重量损失。由表2可见，饵料破碎率均值约为0.4%，而通常以拨轮下料配合之间，有的甚至更高，可见优化后的结构可实现饵料破碎率大幅降低。

表2 饵料破碎率测试实验数据与分析Table 2 Experimental data and analysis of bait crushing rate test

4 结论

（1）为减少下料过程中饵料被拨轮挤压破碎，进行饵料颗粒在下料口处的受力分析，得出拨轮结构对饵料破碎的影响因素，并通过优化下料拨轮的型线，解决下料过程中饵料被挤压破碎的问题。

（2）为减少抛洒过程中饵料被抛洒盘冲击破碎，建立饵料在抛洒盘沟槽作用下的运动学模型，通过优化沟槽型线，减小抛洒盘对饵料的冲击力，解决抛洒过程中饵料被加速造成的破碎问题。通过EDEM 仿真验证了沟槽曲线化改进的效果和必要性，提升了系统的适用性。

（3）基于优化后的结构研制投饵样机，进行饵料播撒实验。实验表明，优化后的机械结构在满足饵料均匀投喂的基础上，实现饵料破碎率较同类结构大幅降低。

后续将结合智能控制技术进行自动投喂研究，提升系统的自动化和智能化水平。