空间热环境下带大型天线卫星的最优姿态控制
梁红利,孟中杰
(西北工业大学航天学院,西安 710072)
0 引 言
在空间通信任务中,为保证天线有效传输信号,带有大型天线的通信卫星需要保持姿态稳定[1]。但是天线振动与卫星姿态运动紧密耦合,给卫星姿态稳定控制造成了极大的困难[2]。
文献[3]将天线振动视为外界干扰,通过状态观测器对扰动进行预估和前馈补偿实现卫星姿态稳定。文献[4]采用动态补偿器抵消天线振动带来的未知干扰,设计了一种基于输出反馈的多目标鲁棒极点配置方法。文献[5]将天线振动视为外界干扰,利用变结构控制对扰动不敏感的优点实现姿态稳定。以上方法均有效削弱了天线振动对姿态的影响,但是没有兼顾控制性能的需求。
最优控制能够兼顾响应快、超调小、抗干扰能力强、控制输入能量少等多种性能需求,实现卫星姿态稳定[6]。文献[7]采用动态规划求解卫星单轴姿态最优稳定控制问题。文献[8]融合动态规划、自适应控制和强化学习,解决了卫星姿态最优稳定控制问题。考虑外界干扰和系统不确定性,文献[9]设计神经网络算法估计外界干扰,构建性能指标函数实现最优控制。文献[10]基于干扰估计建立非线性扰动的上界函数,设计了基于神经网络的最优控制方法。考虑外界干扰引起系统不确定性,文献[11]基于神经网络模型建立性能指标函数并求解哈密顿-雅各比-贝尔曼(Hamilton Jacobi Bellman,HJB)方程实现最优控制。以上方法都通过构建基于干扰估计的性能指标函数实现最优控制,但需要假设外界干扰满足与控制输入相关的匹配条件。文献[12]针对具有非匹配干扰的非线性不确定系统,设计了基于干扰观测器的最优滑模控制方法。文献[13]设计非线性观测器在线估计非匹配干扰,提出一种鲁棒最优滑模控制方法。文献[14]针对具有非匹配扰动的非线性不确定系统,设计了基于干扰估计的最优保性能滑模控制方法。这些方法不需要假设外界干扰满足匹配条件,但是需要提前预知干扰的上界信息。
带有大型天线的卫星在轨运行时会受热环境干扰。尤其当它进出地球轨道阴影区时,环境温度剧烈变化使天线产生热变形与热应力并激发热振动,这会给卫星姿态控制系统带来上界未知的非匹配干扰[15-18]。针对上述难题,本文重点考虑外界干扰的未知非匹配特性,设计一种基于滑模面的自适应近似最优控制方法,实现热环境影响下带大型天线卫星的姿态稳定控制。
1 带大型天线卫星的姿态动力学模型
本文的研究对象是由3颗卫星和2个大型桁架式的天线组合而成的天线卫星系统。由于天线具有类似于梁的动力学特性,基于能量互等原理[1]可将天线等效为连续梁,将卫星视为刚体。此时,系统可简化为“刚体—挠性梁”模型[19-20],如图1所示。
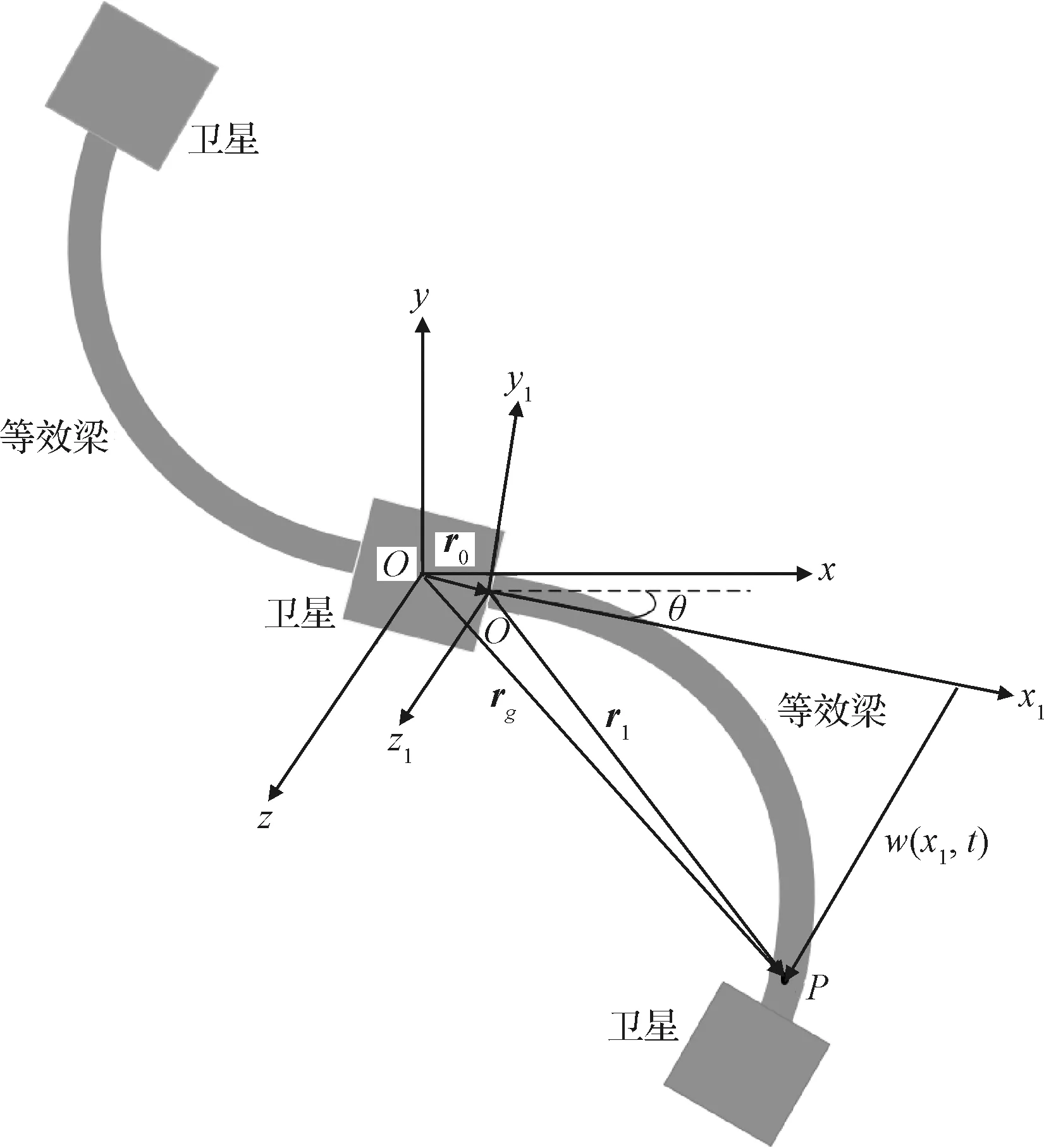
图1 带大型天线卫星的简化模型Fig.1 Simplified model of the satellite with large antenna
设oxyz为惯性系,原点o位于中心刚体质心,ox轴指向初始时刻梁的伸展方向,oy轴垂直于初始时刻梁的伸展方向,oz轴按右手定则确定。ox1y1z1为梁上的浮动坐标系,原点o位于中心刚体与梁的连接点,ox1轴指向梁的伸展方向,oy1轴垂直于梁的伸展方向,oz1轴按右手定则确定。为了便于建立系统动力学模型,提出以下4个假设。
假设1.忽略轨道运动,将两端卫星视为刚体,以中心卫星姿态代表系统整体姿态[1]。
假设2.围绕oz轴的偏航运动和围绕ox轴的滚转运动耦合不明显,忽略耦合作用,重点研究偏航运动[2,21]。
假设3.由于梁的弯曲刚度远小于轴向刚度和扭转刚度,重点研究弯曲运动[19]。
假设4.由于系统为对称构型,建模与分析时只考虑右半部分[19,22]。
假设右侧卫星控制力为fc(t),中心卫星控制力矩为2T(t),右侧等效梁的热应力为dc(x1,t)。梁的长度、线密度和抗弯刚度分别为l0,ρA和EI。梁横向变形位移为w(x1,t),卫星质量为m,半径为r0。中心卫星转动惯量为2J,绕oz轴转角为θ。等效梁上的任意点P在浮动坐标系的位置矢量为r1,它在惯性系的位置矢量为rg。浮动坐标系原点o在惯性系的位置矢量为ro。
在轨道热环境影响下,温度的剧烈变化会激发天线产生热应力与热振动,给系统带来未知干扰。参考文献[15],考虑轨道热环境影响,利用Hamilton变分法建立系统的刚柔耦合动力学模型。其姿态动力学方程和挠性振动方程分别为:
fcφ(l0)ηsinθ+s9χcosθ-χTs10η·
sinθ+T
(1)
(φ(l0))T+s11χ+s11χcosθ
(2)

联立式(1)和(2),将挠性动力学视为姿态动力学的外界干扰,卫星姿态动力学模型为:
(3)

(4)

将式(3)整理为如下形式:
(5)
(6)
由于控制输入矩阵和干扰输入矩阵不相等,控制量u和干扰Δ(x)不匹配,该卫星的姿态控制问题是一个具有未知非匹配干扰和不确定性的非线性系统控制问题。
2 姿态最优控制问题描述
sTQs+uTPu)dτ
(7)
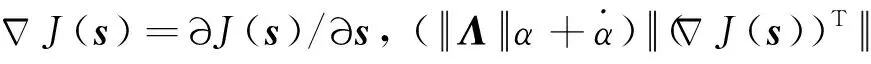
最优性能指标即为J(s)的极小值:
(8)
式中:ψ是容许控制集合。
根据Bellman最优控制理论[17],最优性能指标J*(s)和最优控制律u*(x)满足HJB方程,求解HJB方程可得最优控制律为:
(9)
但是非匹配干扰Δ(x)的上界α(t)未知和系统模型不确定,导致HJB方程不确定,无法直接获得最优解u*(x)。
3 基于滑模面的自适应近似最优控制方法
针对上述姿态最优控制问题,本文设计一种基于滑模面的自适应近似最优控制方法。首先采用基于滑模面的单层评价神经网络[17]逼近最优性能指标函数,解决HJB方程求解困难的问题;然后设计基于状态观测器的干扰估计算法在线估计非匹配干扰的上界α(t),解决未知非匹配干扰问题;最后与滑模控制律结合提高响应速度。控制框图如图2所示。
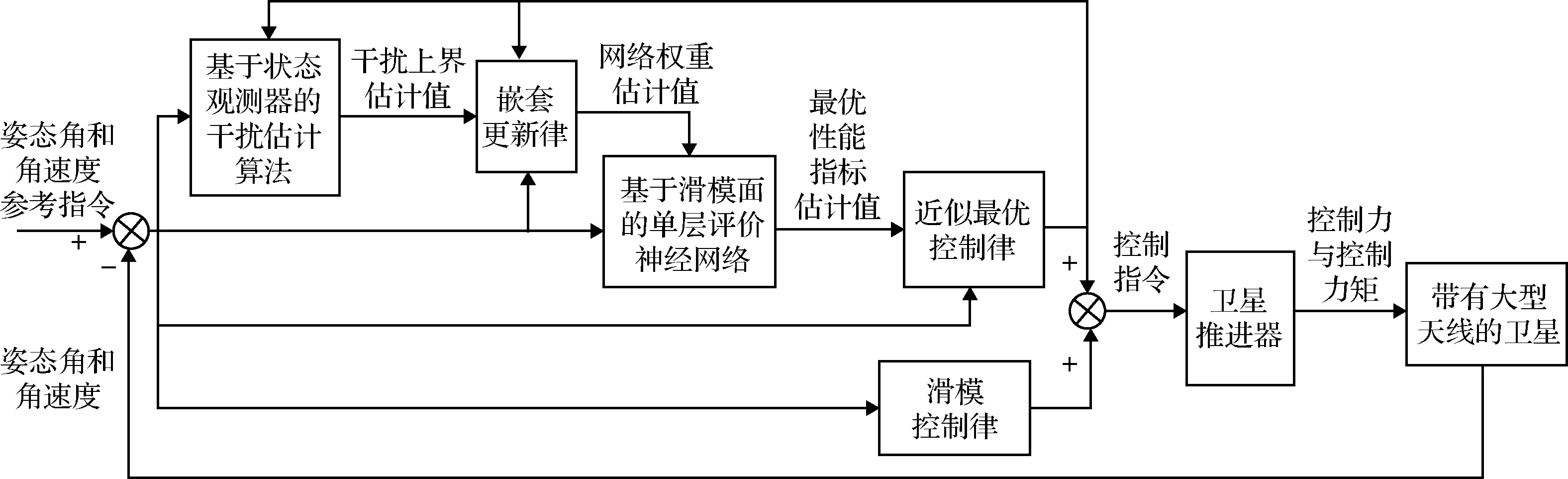
图2 基于滑模面的自适应近似最优控制器Fig.2 Adaptive approximate optimal controller based on sliding mode surface
3.1 基于滑模面的单层评价神经网络
利用神经网络的万能逼近性,最优性能指标函数J*(s)可表示为
(10)
式中:W*∈Rm,σ(s)∈Rm和ε(s)分别为理想权重矢量、激活函数矢量和神经网络逼近误差。m是隐含层神经元个数。
J*(s)关于滑模变量s的偏导数为:
(11)

HJB方程可表示为:
(12)
由于没有逼近误差项ε(s)的信息,无法确定理想权重矢量W*。

(13)
(14)
HJB方程可表示为:
(15)
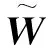
(16)
其中,εα范数有界,即||εα||≤εM,εM是未知非负常数。
(17)
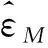
(18)
式中:k1>0是学习率。可以看出,更新律(17)、(18)是一组嵌套更新律。
定理1.针对该卫星系统的姿态最优控制问题,采用基于滑模面的单层评价神经网络逼近HJB方程的最优解,若网络权重更新律为嵌套更新律(17)、(18),则权重矢量的逼近误差动力学渐近稳定。
证.定义李雅普诺夫函数为
(19)
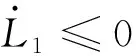
对式(19)求导,再将嵌套更新律(17)、(18)代入,得:
(20)
式中:|·|为矩阵的1范数。
联立式(14)和式(9),得到近似最优控制律为
(21)
但是非匹配干扰上界α(t)未知,导致该近似最优控制律无法获得。
3.2 基于状态观测器的干扰估计
本节主要通过设计状态观测器估计非匹配干扰的上界α(t)。

(22)
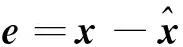
(23)
式中:lη>0是学习率。
联立式(22)和式(5),得到状态观测误差系统为
(24)

由于α在线更新,根据式(7)可知,性能指标函数J(s)可根据干扰实时在线更新。
3.3 基于滑模面的自适应近似最优控制律
为了加快响应速度,引入滑模控制律,设计基于滑模面的自适应近似最优控制律为:
(25)

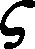
(26)

定理2.针对系统(5),基于滑模面的自适应近似最优控制律(25)和鲁棒项更新律(26)可以保证闭环系统(5)最终一致有界。
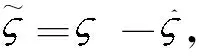
(27)
对上式求导,再联立式(5)、(25)和(26)得:
(28)
式中:0<||B(x)||≤Dg,Dg是未知正常数;κ=||Λ||Dg;λmin(K1)是矩阵K1的最小特征值。
根据式(7)和式(5)可得:
(29)

联立式(28)和式(29),得:
(30)

选择控制参数K1,Q,P使得:
(31)
那么根据李雅普诺夫稳定判据可知该系统的状态最终一致有界。证毕。
4 仿真校验
为了验证设计方法的有效性,本节在典型应用场景下同时利用两种方法进行仿真。1) 本文设计的方法;2) 基于自适应动态规划的鲁棒最优滑模控制[23]。
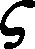
dc(x,t)=Θ(x)β(t)
(32)
式中:函数Θ(x)反映了热应力沿天线轴线的分布情况;x是天线上的点沿轴线的位置坐标;函数β(t)反映了热应力随时间的变化趋势。文献[18]采用有限元软件模拟了天线在该温度变化情况下函数Θ(x)和β(t)的变化情况,如图3所示。
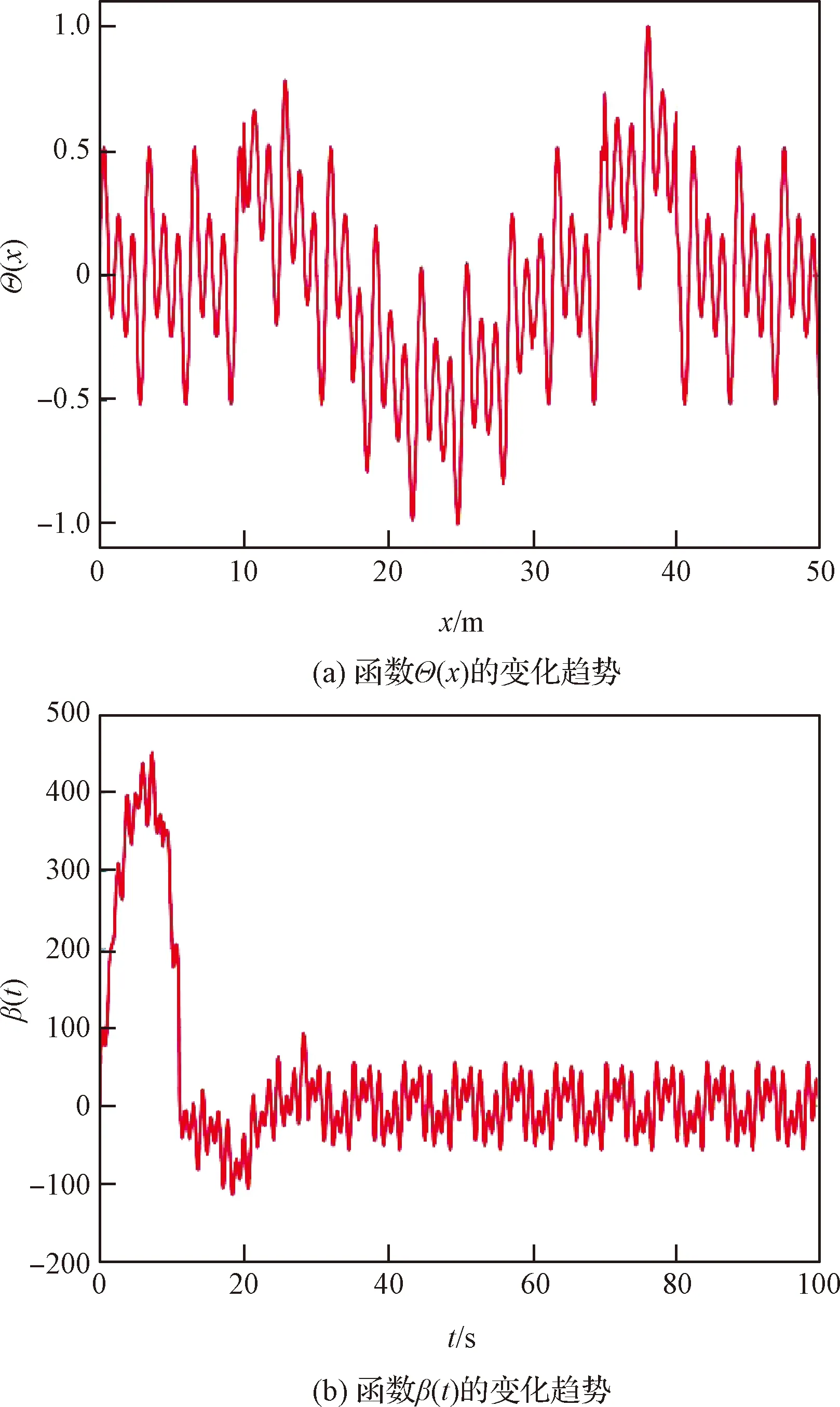
图3 天线热应力的变化趋势Fig.3 Changing trend of the antenna thermal stresses
在上述仿真场景下进行仿真,系统仿真结果如图4~7所示。
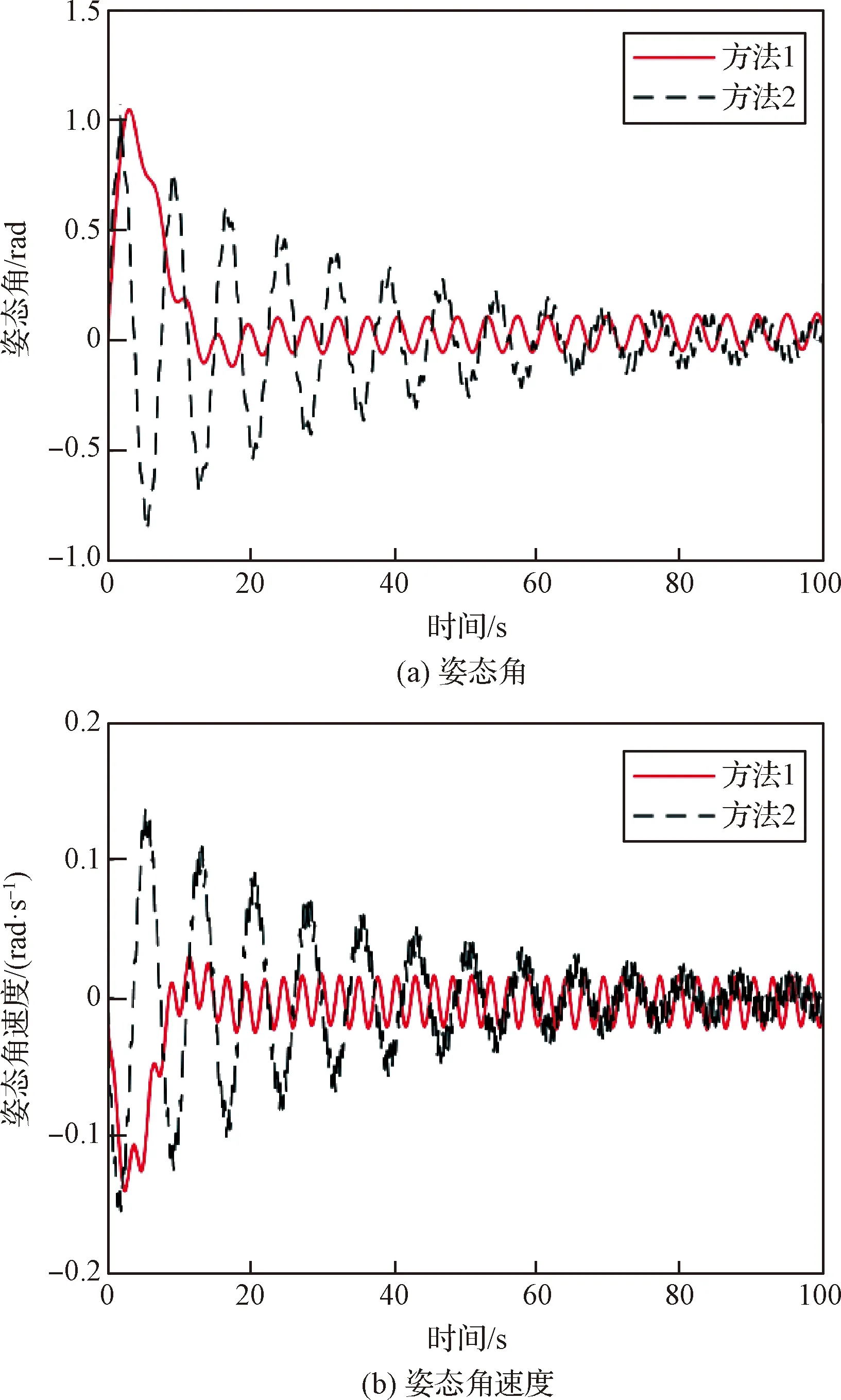
图4 卫星姿态运动Fig.4 Satellite attitude motion
图4是卫星姿态运动曲线,可以看出:两种方法均可实现卫星姿态稳定,且稳态误差相当。但是,利用本文方法,姿态角和角速度的收敛时间都明显小于方法2,因此本文设计的方法具有更好的快速性。图5是天线弹性振动曲线,可以看出:利用本文方法,天线中间位置的振动位移和末端的振动位移都明显小于方法2。但由于未对天线振动实施主动控制,天线残余振动主要依靠自身阻尼衰减。由于空间天线极小的振动阻尼,残余振动衰减很慢。图6是该系统的控制力与控制力矩曲线,可以看出:本文设计方法的控制力与力矩都小于方法2。说明本文方法的控制输入能量更少。同样,由于天线的残余振动,卫星姿态仍受到一定影响。为保持卫星姿态,在仿真末端仍需要输出一定的控制力与力矩,以抵消天线残余振动对姿态运动的干扰。图7是性能指标函数曲线,可以看出:本文方法的性能指标函数值远小于方法2,由于性能指标反映了外界未知非匹配干扰对姿态控制系统的影响,可知本文方法使外界未知非匹配干扰对姿态控制的影响更小,体现了更好的抗干扰能力。

图5 天线弹性振动Fig.5 Antenna flexible vibration

图6 控制力与控制力矩Fig.6 Control force and control torque

图7 性能指标函数J(s)Fig.7 Performance index function J(s)
5 结 论
针对地球轨道热环境下带大型天线卫星的姿态稳定问题,本文设计了一种基于滑模面的自适应近似最优控制方法。首先考虑外界未知非匹配干扰,构造了基于干扰估计、具有在线更新能力的性能指标函数。然后考虑系统不确定性,采用基于滑模面的单层评价神经网络逼近HJB方程最优解,并与滑模控制结合加快响应速度。仿真结果表明:在卫星从轨道阴影区向日照区运行,温度大幅变化的任务场景中,本文方法能以较少的控制能量更快速地实现卫星的姿态稳定控制。但由于天线阻尼较小且本文未对天线进行主动控制,在控制末期,天线仍然保持小幅振动,给卫星姿态带来一定影响,这也是下一步研究工作的重点。

