基于无人机-卫星遥感升尺度的土壤水分监测模型研究

马 仪 黄组桂 贾江栋 罗林育 王 爽 姚一飞

(1.云南电网有限责任公司电力科学研究院, 昆明 650217;2.西北农林科技大学水利与建筑工程学院, 陕西杨凌 712100;3.西北农林科技大学旱区农业水土工程教育部重点实验室, 陕西杨凌 712100)

0 引言

我国西北内陆干旱半干旱区域一直存在明显的水资源短缺问题,发展缺水地区地表土壤水分快速、合理、高精度的监测,对于指导农业生产建设、荒漠植被恢复以及灌溉制度制定有着重要的作用和意义。传统的土壤水分含量测量方法大多针对地面采样点进行研究,虽然精度较高,但该方法不仅测量的范围有限,取样的代表性较差,更需耗费大量的人力、物力和财力,同时也无法实现大范围、高效率的测量效果[1]。而遥感因其具有无损、便捷快速、可进行大范围监测等优势,逐渐开始应用于地表土壤水分的监测研究。早在20世纪70年代,美欧等国家便开始利用卫星遥感进行土壤水分的监测研究[2]。虽然取得了不少进展,但受限于平台,往往难以获得大尺度范围和高精度两者兼具的监测结果。无人机(Unmanned aerial vehicle,UAV)是一种能携带多种任务设备,兼具低成本、低损耗、可重复使用等优点的无人驾驶航空器[3],当在该航空器上装载多光谱或高光谱传感器时便可以快速、较低成本、便捷灵活地获取高精度的农田作物信息,以满足精准农业的相关需求[4],但作用的尺度范围较小。一般而言,单独利用卫星或无人机遥感无法实现高精度且大尺度范围的土壤水分监测,因此有必要发展合理的尺度转换方法将二者的优势结合,以快速实现大尺度范围上高精度的地表地物信息监测。在遥感领域,尺度转换就是将数据或信息从一个尺度变换到另一个尺度的过程,将从高分辨率到低分辨率的尺度转换称为升尺度,反之则称为降尺度[5]。采用尺度转换方法将多源遥感数据相结合以监测地表土壤水分和盐分的可行性已被诸多学者验证。如冯文哲等[6]分别利用卫星和无人机获取遥感影像数据,引入多种机器学习算法构建土壤盐渍化监测模型,并使用升尺度转换方法,较大幅度地提高了卫星遥感对土壤盐渍化的监测精度。岳朝政[7]提出了基于变分贝叶斯推断和非参数贝叶斯的土壤水分空间升尺度法。陈俊英等[8]以卫星和无人机两种不同遥感为数据源,采用改进的TsHARP法进行线性回归函数趋势面的构造以构建土壤盐渍化监测模型,提高了卫星遥感对土壤盐渍化的监测精度。张智韬等[9]基于加权算法将无人机数据尺度上推以修正卫星遥感数据,有效提高了土壤含盐量监测精度。土壤中的水分和盐分常常相互伴随交互、联系紧密[10],如柯增鸣[11]发现在0～20 cm和20～40 cm土层的土壤水分与土壤盐分在土壤相对含水率为52%～75%下具有较高的相关性,张术伟等[12]在探究黄河三角洲壤土水盐变化时发现,在升盐过程中,土壤表层水盐呈现正向线性关系,此外土壤中的水分和盐分在光谱吸收带的范围有着较大的重合[10],理论上可以采取尺度转换手段将多源遥感数据相结合的方式,应用于土壤水分的监测研究。然而,目前在协同多源遥感数据以开展升尺度的土壤水分监测方面的相关研究仍较少。基于此,本研究以内蒙古河套灌区为研究对象,分别采用重采样和TsHARP升尺度法,将无人机遥感数据尺度上推以修正卫星数据,通过引入不同算法构建升尺度修正后GF-1卫星遥感数据源下不同深度的土壤含水率反演模型,以期实现大尺度、高精度的土壤水分反演,为干旱、半干旱地区的土壤含水率监测提供技术依据。

1 材料与方法

1.1 研究区概况

选取内蒙古河套灌区解放闸灌域沙壕渠试验站为研究区。河套灌区位于我国黄河流域上游,平均海拔1 km以上,是我国第三大灌区[13]。解放闸灌域处于河套灌区西部,属干旱半干旱区[14]。而沙壕渠是解放闸灌域的一个独立体,位于内蒙古自治区巴彦淖尔市杭锦后旗,其土壤类型大多为粉质粘壤土,平均干容重约为1.46 t/m3,年降水量不到200 mm,年蒸发量却在2 000 mm以上,蒸降比超过10[15]。由于气候、地形条件、土质因素及人为的不合理灌溉等因素,导致该地区的土壤盐渍化问题较为突出。

本次试验在沙壕渠内进行(图1),在研究区内分散选取了4块土地,进行了无人机飞行试验,并均匀布置采样点,同步采集土壤样本,以计算土壤含水率。

1.2 遥感数据获取与处理

1.2.1卫星遥感数据

卫星影像数据从中国资源卫星应用中心(http:∥www.cresda.com/CN/)下载获取。本研究选用的卫星遥感影像成像时间为2019年7月30日,空间分辨率为16 m,包括b1、b2、b3、b4共4个波段,分别对应蓝(B)、绿(G)、红(R)和近红外(NIR),谱段范围分别为0.45～0.52 μm、0.52～0.59 μm、0.63～0.69 μm和0.77～0.89 μm。利用ENVI软件对获取的影像进行辐射定标、几何精度校正、大气校正、裁剪等预处理,之后将实测的120个采样点坐标导入遥感影像,提取各波段的反射率,用于后续光谱指数计算及土壤含水率反演。

1.2.2无人机多光谱遥感数据

使用大疆创新科技有限公司生产的M600型六旋翼无人机获取无人机遥感影像。多光谱传感器型号为Micro-MCA,包括b1、b2、b3、b4、b5、b6共6个光谱波段,分别对应蓝(B)、绿(G)、红(R)、红边(NIR)、近红外1(NIR1)以及近红外2(NIR2),中心波长分别为490、550、680、720、800、900 nm。于2019年7月15—25日获取无人机多光谱影像。飞行当天天气晴朗,无人机按照定好的航线飞行,飞行高度为120 m,多光谱相机镜头垂直向下,此时影像所对应的地面分辨率约为0.065 m。使用多光谱相机配套的Pixel wrench图像编辑软件对获取的无人机遥感影像进行校正、裁剪、拼接、合成等相关处理,导出tif格式的多光谱影像。最后将采样点的经纬度导入ENVI软件,提取影像中对应采样点的灰度,通过参考白板进一步计算各波段反射率。

1.3 土壤样本采集处理与含水率计算

土壤样本的采样时间与无人机影像获取时间同步,与卫星遥感影像数据获取时间相近。采用五点取样法进行采样,共布设120个土壤采样点,采样点深度分别为0～20 cm、20～40 cm和40～60 cm,并采用手持GPS定位,记录采样点的地理坐标。将野外采集到的各深度的120个土样快速装入已知质量的干燥铝盒,密封并标记好后称量,经105℃、24 h恒温处理后称量,计算土壤质量含水率θm,计算式为

(1)

式中W1——空铝盒质量

W2——湿土加铝盒质量

W3——干土加铝盒质量

将因试验记录及计算错误所得土壤含水率为负值的数据剔除,最终剩余101个实测土壤样本用于本次研究。将101个土壤含水率样本从小到大排序,建模集与验证集按照比例2∶1等间隔分配,以确保建模集与验证集分布均匀。

1.4 光谱指数计算与全子集筛选

一般而言,仅用个别波段难以充分提取地物光谱信息以及构建高精度的土壤含水率反演模型,因此许多学者通过建立光谱指数以更好地反映地物信息。如曹雷等[16]研究发现,SI-T、S5等盐分指数对土壤盐渍化较为敏感,具有较好的预测能力;差值植被指数(Difference vegetation index,DVI)常被应用于光学遥感反演土壤水分[17]。结合前人研究经验以及考虑到灌区较高植被覆盖度和一定盐渍化问题的实际情况,在GF-1卫星遥感数据的波段反射率基础上,引入应用广泛的植被指数和盐分指数建立遥感图像与土壤含水率的定量关系,分别为盐分指数SI2、盐分指数S3、盐分指数S5、盐分指数S6、盐分指数SI-T、亮度指数(Brightness index,BI)、土壤调节植被指数(Soil adjusted vegetation index,SAVI2)、垂直干旱指数(Perpendicular drought index,PDI)、转换型土壤调节植被指数(Transformed soil-adjusted vegetation index,TSAVI)、差值植被指数(DVI),相关计算公式见表1。

表1 光谱指数汇总Tab.1 Summary of spectral index

采用全子集筛选法筛选出自变量(敏感波段和光谱指数)的最优组合。该法假设有M个自变量,对M中的P个变量(1≤P≤M,P、M均为整数)分别与因变量做最小二乘拟合,拟合出1～P个预测变量模型;在1～P个模型中,根据调整后决定系数(Coefficient of determination,R2)最大原则,综合考虑均方根误差(Root mean squared error,RMSE)、赤池信息准则(Akaike information criterion,AIC)和施瓦茨信息准则(Schwarz information criterion,SIC),从P个模型中选出一个最优自变量组合。通过Matlab软件完成全子集筛选算法模型的构建。

1.5 模型建立

1.5.1多元线性回归模型

多元线性回归(Multiple linear regression, MLR)是指在相关变量中,将一个变量视为因变量,其它一个或多个变量视为自变量,建立多个变量之间线性的数学模型数量关系式[24]。多元线性回归是一元线性回归的扩展,通常采用最小二乘法对参数进行估计。因变量y与自变量X1、X2、…、Xn之间线性关系为

y=β0+β1X1+β2X2+…+βnXn+ε

(2)

式中β0、β1、…、βn——回归系数

ε——服从正态独立同分布的随机误差项

通过Matlab软件完成多元线性回归模型的建模与验证。

1.5.2BP神经网络模型

BP神经网络(Back propagation neural network,BPNN)是一种根据误差逆向传播算法训练的多层前馈神经网络[6]。该机器学习模型的拓扑结构一般由输入层、隐藏层、输出层组成,本研究采用3层BP神经网络,其中输入层与输出层均采用线性激活函数(purelin),隐含层采用双曲正切激活函数(tansig),含有10个神经元的单层网络,为防止数据分析因为不同的量纲得出不同的结果,对输入层和输出层数据进行归一化处理。模型的各参数设置为:训练拟合目标误差为0.1%,网络的学习速率为0.05,最大训练次数为6 000次,其余参数取默认值。通过Matlab软件完成BP神经网络模型的建模和验证。

1.5.3支持向量机模型

支持向量机(Support vector machines,SVM)是一类按监督学习方式对数据进行二元分类的广义线性分类器,从功能上可分为分类和回归两类[25],可用于非线性分类问题[26],能够较好地避免“离散值多”的问题。本研究将目前应用广泛的径向基核(RBF)作为核函数,惩罚参数C和核参量g则通过在模型中设置循环来选择和调整,同样对输入和输出数据进行归一化处理,在Matlab软件进行支持向量机模型的构建和验证。

1.6 升尺度转换方法

1.6.1重采样升尺度法

在遥感领域,重采样是一种影像数据重新组织过程中的灰度处理方法[27]。常用的重采样方法有最邻近法、双线性内插法、立方卷积内插法、像元聚合法等。本研究采用像元聚合法实现对无人机遥感影像的重采样。像元聚合法是对所有的输出像元值有贡献的像元平均值进行采样,通过ENVI软件Rezise data功能中的Pixel aggregate实现。用重采样升尺度到分辨率16 m的无人机遥感数据构建的光谱指数修正GF-1卫星数据光谱指数,具体为分辨率16 m的无人机遥感数据的波段反射率及构建光谱指数乘以对应的GF-1卫星数据的波段反射率及光谱指数,得到升尺度修正后的GF-1卫星遥感数据。

1.6.2TsHARP升尺度法

TsHARP升尺度法主要通过构造趋势面进行尺度转换,有学者将其应用于土壤盐渍化的升尺度研究[28],但仅进行了传统的线性回归模型函数趋势面之间的构造。本文通过将目前应用广泛的BP神经网络和支持向量机算法进行趋势面的构造,以实现土壤水分的升尺度研究,提高卫星遥感对土壤含水率的反演,该升尺度法的主要步骤如下:

首先建立无人机尺度上土壤含水率与趋势面因子间的关系,公式为

S=F(B′)

(3)

式中S——无人机分辨率0.065 m尺度上采用趋势面因子反演的土壤含水率

F——无人机分辨率0.065 m尺度上趋势面反演函数或模型,同样适用于升尺度到GF-1卫星分辨率16 m尺度上土壤含水率与趋势面因子间的反演

B′——无人机分辨率0.065 m尺度上的趋势面因子

由于受到土壤盐分等因素的影响,趋势面因子总是很难完全反映土壤含水率的分布情况,表现为无人机高分辨率0.065 m尺度上的转换残差ΔS,在本文中也认为等于GF-1卫星尺度上的转换残差ΔS1,计算公式为

ΔS=S′-S=ΔS1

(4)

式中S′——实测土壤含水率

升尺度修正后GF-1卫星数据源下反演的土壤含水率由GF-1卫星数据应用无人机尺度上建立的趋势面计算的土壤含水率和卫星尺度上的转换残差构成,计算公式为

S16=F16(B16)+ΔS1=F(B16)+ΔS1

(5)

式中S16——升尺度修正后GF-1卫星数据下反演的土壤含水率

B16——GF-1卫星分辨率16 m尺度上的趋势面因子

1.7 模型精度评价指标

根据调整后的决定系数R2、均方根误差(RMSE)、赤池信息准则(AIC)和施瓦茨信息准则(SIC)来综合评价全子集筛选效果;通过调整后R2、RMSE综合评价升尺度前后各模型的精度与稳定性。调整后R2可以反映建模和验证的拟合效果,RMSE可以反映反演值与实测值之间的偏差度,其中R2越接近1,RMSE越小,说明模型精度越高。AIC和SIC能够在一定程度上衡量统计模型的复杂度和拟合优良性,其参数值越小表示该模型能够以最少自由变量最好地解释因变量。

2 结果与分析

2.1 相关性分析与全子集筛选确定的最优自变量组合

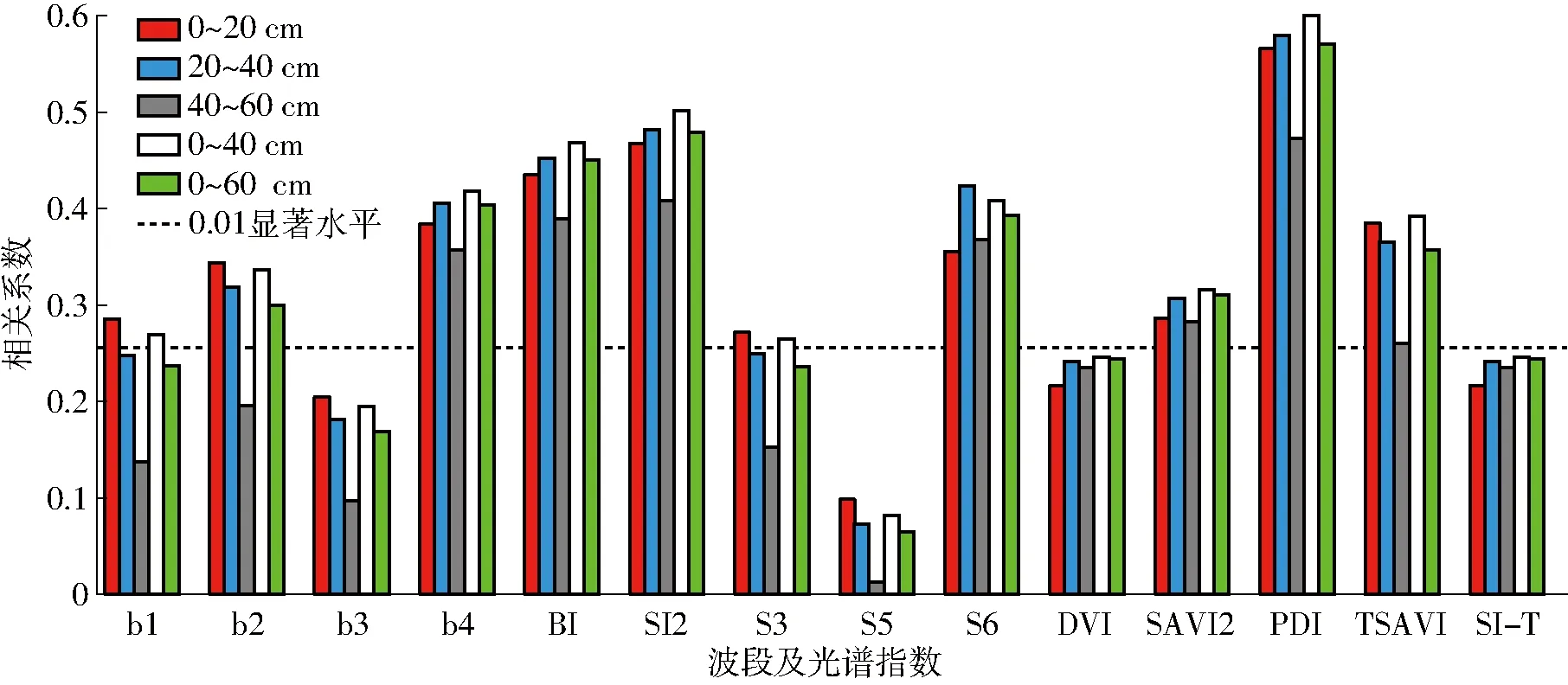
图2 波段及光谱指数与不同深度土壤含水率的皮尔逊相关系数Fig.2 Pearson correlation coefficient of band and spectral index and soil moisture content at different depths

参考相关系数检验临界值表进行显著性检验,当样本数据点为101时,其对应的自由度为99,当相关系数的绝对值大于0.255时,达到0.01显著性水平。从图2可以看出,除b3、S5、DVI和SI-T外,其它波段及光谱指数与土壤含水率的相关系数大于0.255,达到0.01显著水平,分析认为绿波段b2位于绿色植物的绿色反射率附近,对植物的绿反射敏感;而近红外波段NIR处于植物的高反射区,为植物识别通用波段,与土壤含水率相关性较强,故b2、NIR波段及基于该两波段建立的BI、SI2、SAVI2、PDI等光谱指数与土壤含水率表现出较强的相关性。相较于其它深度土壤含水率,深度40～60 cm的土壤含水率与各波段及光谱指数的相关系数更小,并未表现出较强的相关性,这与文献[29]研究结果一致,可能原因是随着土壤深度增加,土壤内部环境情况越发复杂,遥感作用于土层的能力逐渐下降。

将波段反射率和光谱指数作为自变量,实测土壤含水率为因变量,构建全子集筛选算法模型,根据验证集调整后R2最大原则,综合考虑RMSE、AIC和SIC等评价指标,确定不同深度下波段反射率与光谱指数之间的最优变量组合,结果如表2所示。

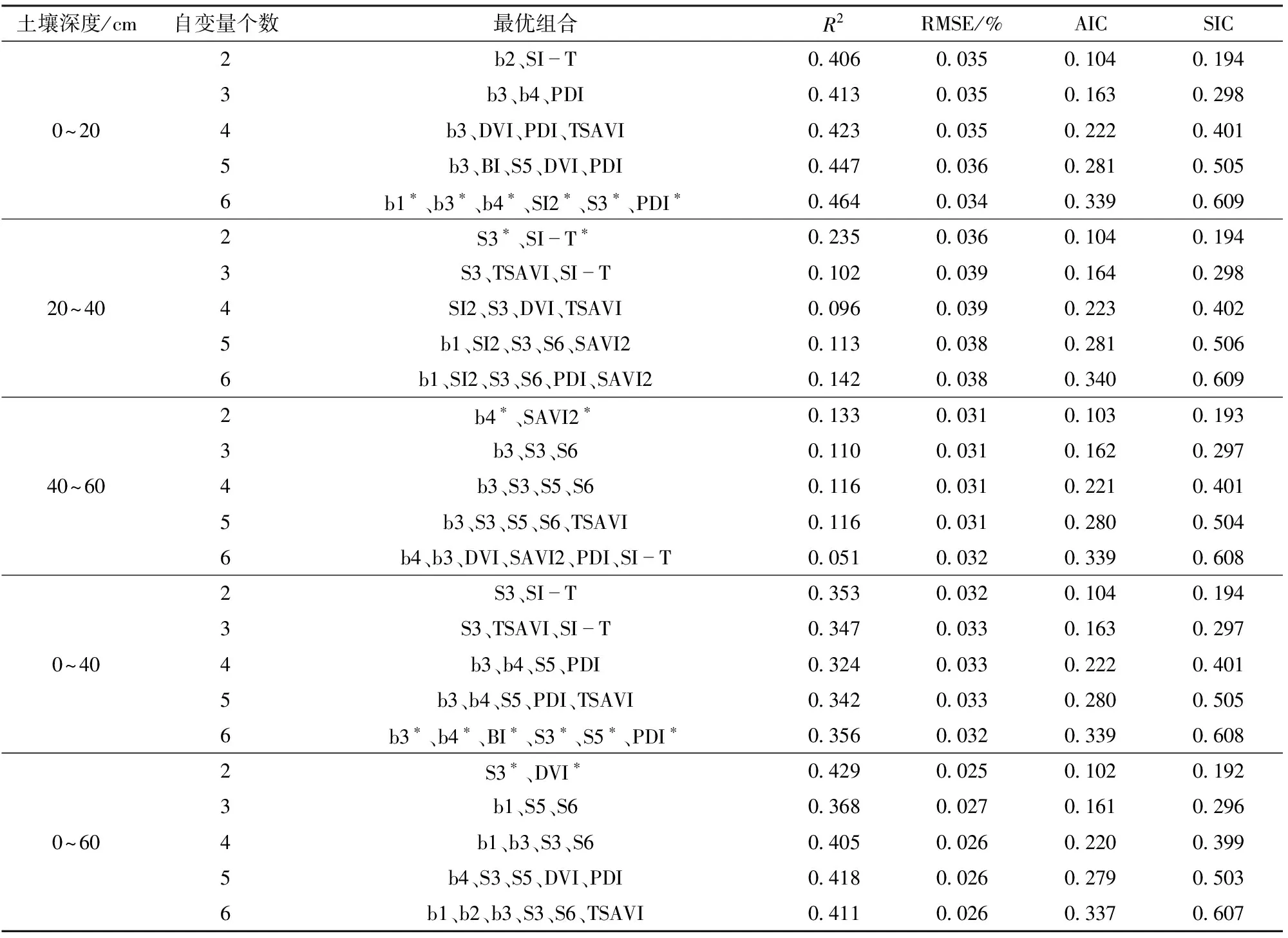
表2 基于全子集筛选的GF-1卫星数据源下最优变量组合Tab.2 Optimal variable combination under GF-1 satellite data source based on full subset screening

从表2可以看出,0～20 cm、0～40 cm和0～60 cm 3个深度下的R2达0.324以上,其中0～20 cm和 0～60 cm整体达0.368以上,拟合效果较好;而深度40～60 cm下的R2仅有0.10左右,拟合效果较差,原因可能是该深度土壤含水率与各光谱变量的相关性较差。各深度下的AIC和SIC均随着自变量个数的增多而呈现逐渐上升的趋势,这是因为随着自变量个数的增加,模型的拟合效果可能会有所提升,但会受到一定的“惩罚”。各深度下的RMSE大多在0.03%上下波动变化,且随着R2的增大呈现减小趋势。不同深度的敏感光谱特征变量总体上是一致的,每一种光谱特征变量在其它深度中均有出现,如S3、DVI等,在不同深度最优变量组合的选择上以最大R2为首要考虑条件(RMSE与此同时也最小)进行。如深度0～20 cm下自变量个数为6时其R2最大,RMSE最小,故选择b1、b3、b4、SI2、S3和PDI作为该深度下的最优变量组合,同理筛选出深度20～40 cm的最优变量组合为S3、SI-T;深度40～60 cm的最优变量组合为b4、SAVI2;深度0～40 cm的最优变量组合为b3、b4、BI、S3、S5、PDI;深度0～60 cm的最优变量组合为S3、DVI。

2.2 基于重采样升尺度法的不同深度土壤含水率反演模型

采用全子集筛选法对升尺度修正后的波段反射率和光谱指数组成的自变量与实测土壤含水率构成的因变量所构建的模型进行一一列举,通过验证集调整后R2最大原则,综合考虑RMSE、AIC和SIC等评价指标,筛选出不同深度下的最优自变量组合,结果如下:0～20 cm为b1、S3、S6、TSAVI,20～40 cm为b1、b3、S3,40～60 cm为b1、b2、b3、b4、S3、SAVI2,0～40 cm为b2、b3、S3、S6、SI-T,0～60 cm为b2、S3、S5、S6、SI-T。

以全子集筛选出的升尺度修正后GF-1卫星数据下的最优变量组合为自变量,实测土壤含水率为因变量,运用多元线性回归、BP神经网络以及支持向量机算法构建不同深度下土壤水分反演模型,并与直接采用GF-1卫星数据源构建的土壤水分反演模型进行对比,评价升尺度修正前后GF-1卫星遥感对土壤含水率的反演效果。

2.2.1多元线性回归模型

由表3可知,升尺度修正后的0～20 cm和40～60 cm MLR模型的反演精度较升尺度修正前有明显的提升,二者验证集的R2分别提高0.211、0.180,分析认为重采样中的像元聚合(Pixel aggregate)对输出的所有有贡献的像元做了取均值处理,能够一定程度上减小建模集与验证集划分不均的影响。土壤深度 0～40 cm的反演效果较好,模型的R2达到0.530,RMSE为0.028%。与升尺度修正前相比,5种深度模型的反演精度均有较为明显的提高,RMSE有一定程度上的降低,说明该升尺度方法有效。

两组患者均无心源性死亡和再发心肌梗死（0例），治疗组和对照组分别有5例、6例患者行靶血管重建。两组患者MACE比较，差异无统计学意义（P＞0.05）。

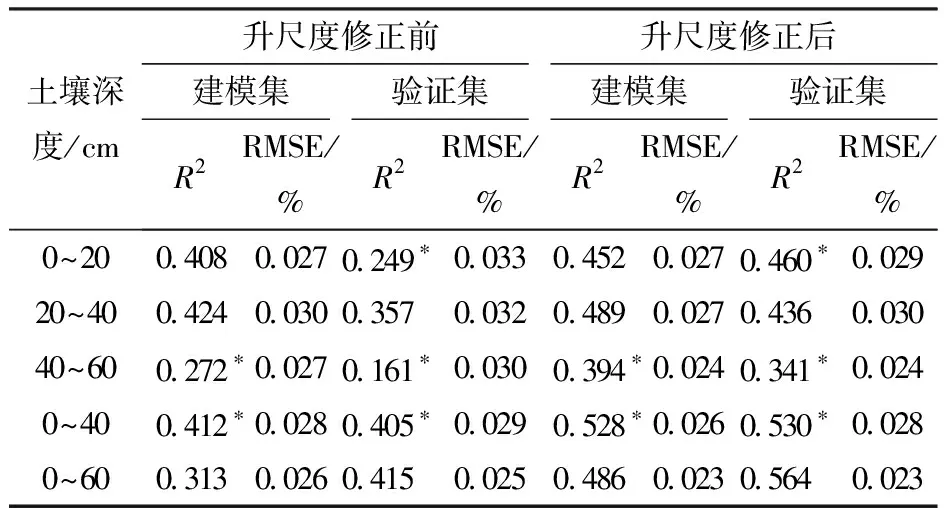
表3 重采样法下不同深度土壤含水率的多元线性 回归模型精度Tab.3 Precision of MLR model of soil moisture content at different depths by resampling method

2.2.2BP神经网络模型

由表4可知,升尺度修正后GF-1卫星数据下的各深度BPNN模型的R2整体提高0.11左右,部分深度如0～20 cm和0～60 cm BPNN模型的R2提高0.15左右,RMSE整体在0.031%以下,均比升尺度修正前明显降低。各深度BPNN模型建模集与验证集的R2相近,无过拟合或欠拟合现象,模型的拟合效果较好。升尺度修正后的40～60 cm BPNN模型的反演精度R2明显低于其它深度,建模与验证效果较差,不适宜进行土壤含水率反演。

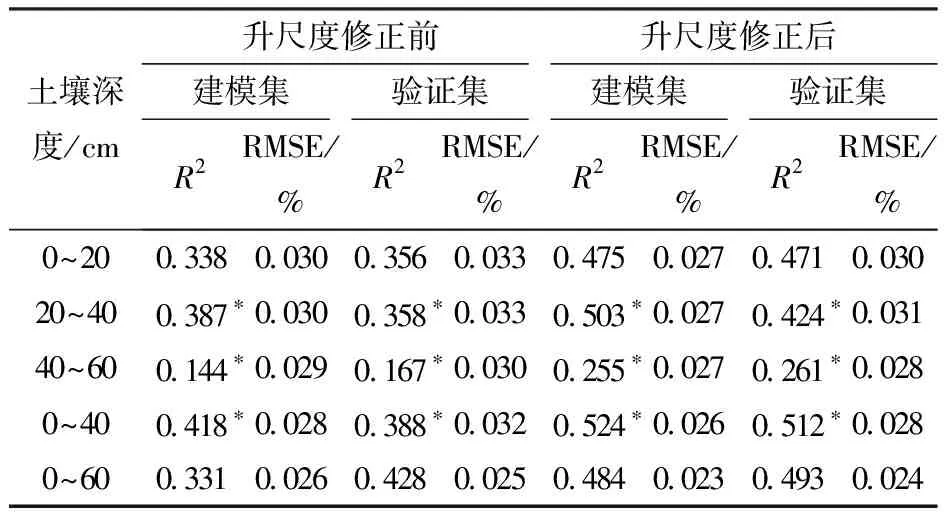
表4 重采样法下不同深度土壤含水率的BP神经网络 模型精度Tab.4 Precision of BPNN model of soil moisture content at different depths by resampling method

2.2.3支持向量机模型

由表5可知,在5种不同深度的升尺度修正后SVM模型中,0～40 cm和0～60 cm SVM模型的R2较升尺度修正前提升最明显,其中,0～40 cm SVM模型的R2提升0.176;0～60 cm SVM模型的R2提升0.158,R2达到0.571,RMSE降低至0.022%,降幅15.4%,为最优深度反演,而其它3个深度SVM模型的反演精度也有明显幅度的提高。升尺度修正后GF-1卫星数据下部分深度SVM模型的反演精度R2最大能提高近0.176,RMSE对应升尺度修正前有较为明显的降低,表明该升尺度法能提高GF-1卫星遥感对土壤含水率的反演精度。

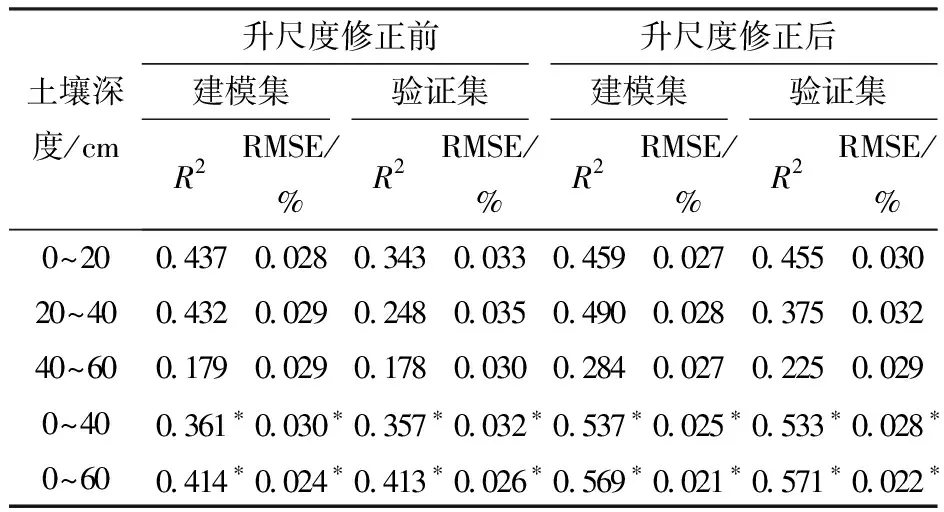
表5 重采样法下不同深度土壤含水率的支持向量机 模型精度Tab.5 Precision of SVM model of soil moisture content at different depths by resampling method

2.3 基于TsHARP升尺度法的不同深度土壤含水率反演模型

由2.1、2.2节可知,深度40～60 cm下各土壤水分反演模型的建模效果明显较其它深度差,不适宜进行土壤水分反演。实际上,随着土层深度的增加,遥感作用于地表的能力逐渐下降,越深处的土壤水分反演显然不合理甚至是错误的。因此,在本节TsHARP升尺度法中只进行深度0～20 cm、20～40 cm、0～40 cm及0～60 cm土壤含水率反演模型的建立与分析。

2.3.1多元线性回归模型

由表6可知,与升尺度修正前相比,各深度模型的反演精度有较为明显的提高,除0～20 cm MLR模型外,其它3种深度模型R2整体从0.4左右提升至0.5以上。其中,0～20 cm MLR模型验证集的R2较升尺度修正前提升0.141,0～60 cm MLR模型建模集的R2较升尺度修正前提升0.213,提升幅度明显。升尺度修正后的各深度MLR模型的RMSE整体有所降低,说明该升尺度法在提高GF-1卫星遥感对土壤水分的反演精度可行。

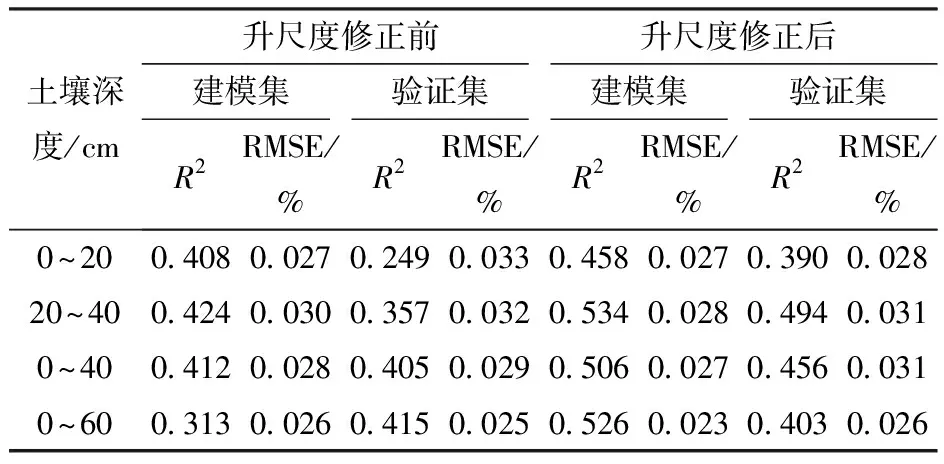
表6 TsHARP升尺度法下不同深度土壤含水率的 多元线性回归模型精度Tab.6 Precision of MLR model of soil moisture content at different depths by TsHARP scale-up method

2.3.2BP神经网络模型

由表7可知,除0～40 cm BPNN模型外,其它3种深度模型的反演精度R2整体达到0.7以上,较升尺度修正前显著提高,RMSE整体下降明显。其中升尺度修正后的0～60 cm BPNN模型的R2最高提升至0.829,RMSE最低降至0.015%,降幅达到40%,为最优反演。与2.3.1节MLR模型相比,各深度BPNN模型的反演效果有着显著的改善,明显优于多元线性回归算法,说明运用BP神经网络算法构建趋势面可行, TsHARP升尺度法的优势能得以较好地展现。

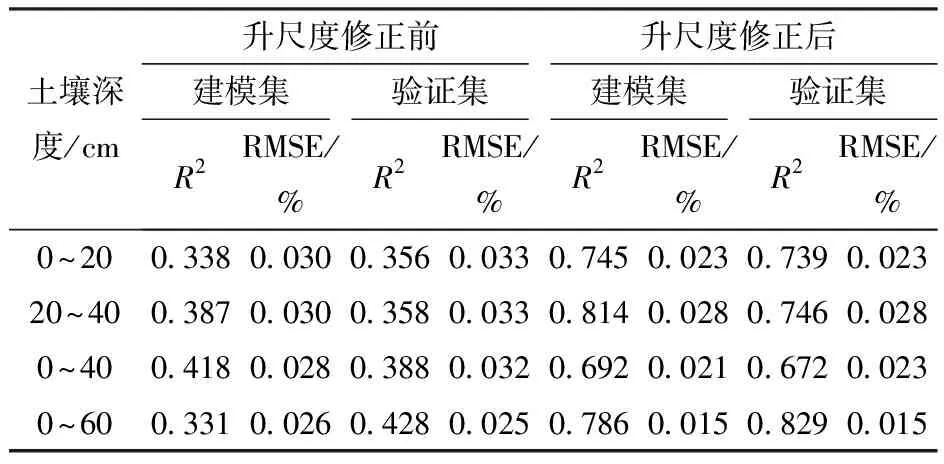
表7 TsHARP升尺度法下不同深度土壤含水率的 BP神经网络模型精度Tab.7 Precision of BPNN model of soil moisture content at different depths by TsHARP scale-up method

2.3.3支持向量机模型

由表8可知,升尺度修正后4种深度SVM模型的R2达到0.6以上,与升尺度修正前相比有明显提高;除20～40 cm SVM模型验证集外,其它深度模型的RMSE均对应升尺度修正前明显降低。其中,0～20 cm、0～40 cm和0～60 cm SVM模型R2较升尺度修正前提升最明显。与2.3.2节基于BP神经网络算法的TsHARP升尺度法在提高反演模型精度上所得结论相似,运用支持向量机的机器学习算法构造趋势面能有效发挥TsHARP升尺度法的效果以提高模型反演精度。

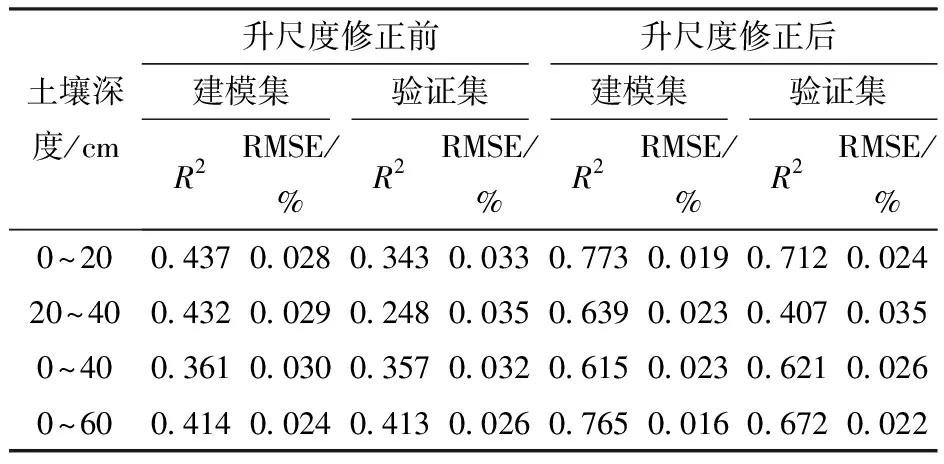
表8 TsHARP升尺度法下不同深度土壤含水率的 支持向量机模型精度Tab.8 Precision of SVM model of soil moisture content at different depths by TsHARP scale-up method

2.4 升尺度反演模型综合评价

由于基于TsHARP升尺度法的修正后GF-1卫星数据下只进行了深度0～20 cm、20～40 cm、0～40 cm和 0～60 cm土壤含水率的反演,故以下主要对比这4种不同深度在基于重采样和TsHARP升尺度法的修正后GF-1卫星数据下构建的土壤含水率反演模型。将两种升尺度方法下采用不同算法构建的不同深度土壤含水率反演模型的评价指标R2绘制成柱形图,以直观对比不同深度不同模型的反演精度,结果如图3所示。

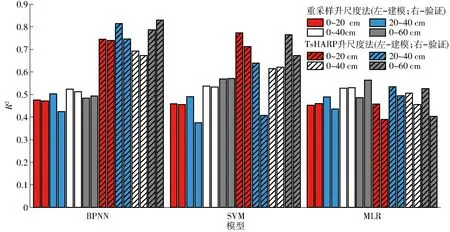
图3 基于两种升尺度法的不同深度下土壤含水率反演模型对比Fig.3 Comparison of soil moisture inversion models at different depths based on two scale-up methods

由图3可知,重采样升尺度法下SVM模型的反演精度最高,而MLR模型整体略优于BPNN模型,即精度由高到低依次为SVM、MLR、BPNN;TsHARP升尺度方法下采用BPNN和SVM两种机器学习算法构建的反演模型均优于MLR算法,而BPNN算法又整体优于SVM算法,即精度由高到低依次为BPNN、SVM、MLR。

采用机器学习算法的TsHARP升尺度法构建的反演模型精度较高且明显优于基于多元线性回归算法,TsHARP升尺度法下反演模型的R2可达0.7以上,说明采用BPNN和SVM算法构造趋势面进行升尺度转换可行。

对于基于多元线性回归算法的重采样和TsHARP升尺度法中,两种不同升尺度法下的不同深度MLR模型的反演精度整体相差不大,而TsHARP升尺度法下的4种不同深度BPNN和SVM模型的反演精度R2均明显高于基于重采样升尺度法(重采样升尺度法下反演模型最大R2约为0.57),说明TsHARP升尺度法整体上优于重采样升尺度法。

2.5 沙壕渠灌域土壤含水率反演

由上述可知,TsHARP升尺度法下0～60 cm BPNN模型的反演效果最好,故选用该模型反演河套灌区内整个沙壕渠的土壤含水率空间分布情况,结果如图4所示。

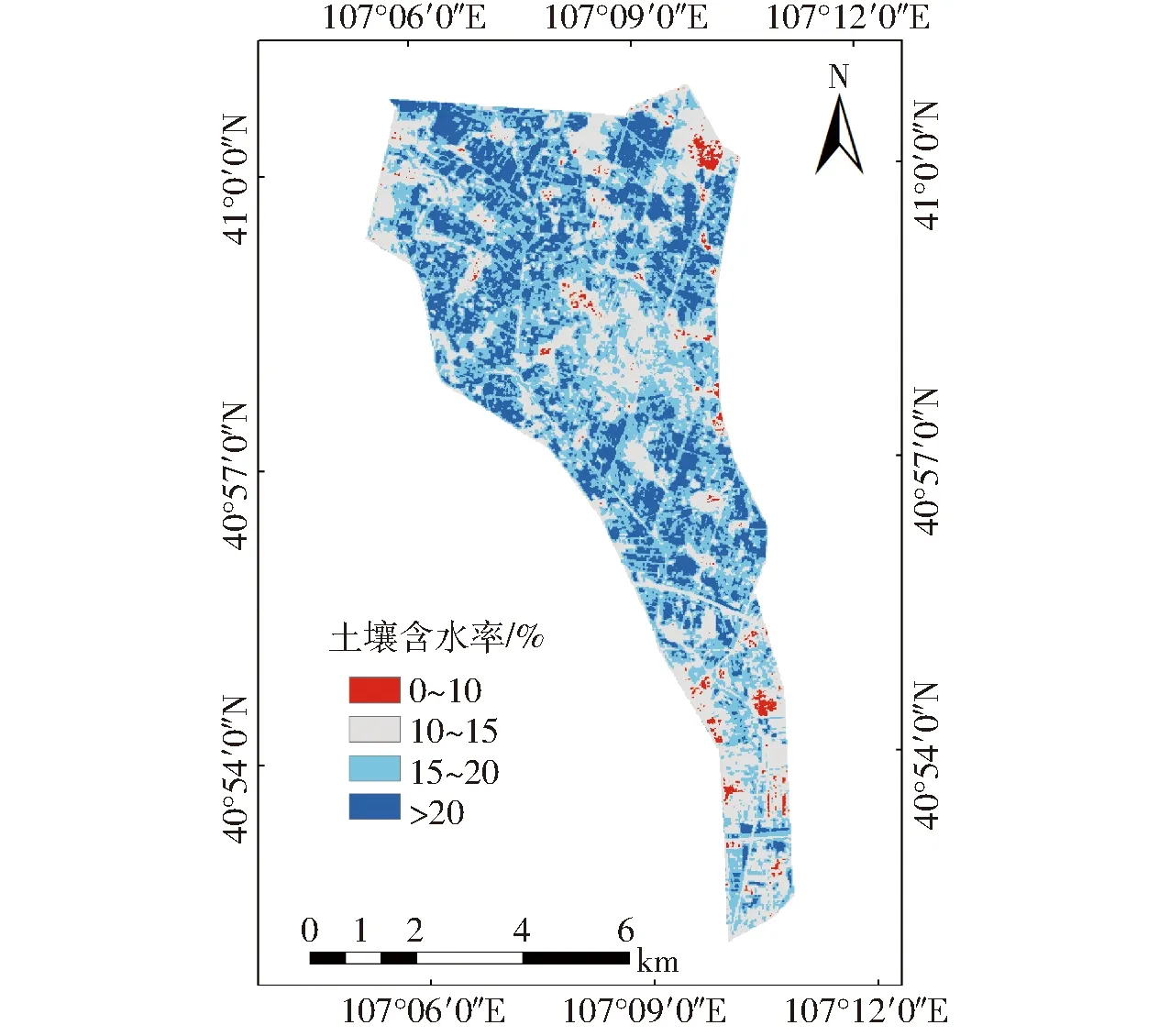
图4 沙壕渠土壤含水率反演结果Fig.4 Inversion result of soil moisture content in Shahaoqu

由图4可知,土壤含水率在0～10%、10%～15%、15%～20%和大于20%分别约占整个沙壕渠研究区的15%、38%、24%和23%,根据内蒙古土壤墒情类型及其含水率等级指标[30],认为土壤含水率低于15%时便出现干旱,而沙壕渠灌域约有53%的区域的土壤含水率低于15%(主要分布在中部、西北部和南部),说明整个沙壕渠灌域较为干旱缺水,这与该区域处于西北内陆干旱半干旱区、整体缺乏水资源的实际情况相符。同时也可以看到沙壕渠土壤含水率高于15%的区域占比约47%,其原因可能是7月下旬气温较高,作物需水量较大,灌区进行了较多次的人为引水灌溉以保证作物生长发育所需的水分,故该时间段内作物种植区域的土壤水分含量能维持在一定水平。

3 讨论

本文旨在分析升尺度修正前后GF-1卫星遥感数据源下不同波段及光谱指数与不同深度土壤含水率之间的统计关系,建立土壤水分反演模型,为灌区进行农业生产及干旱监测提供依据。一般而言,受限于遥感平台,仅基于单一的低、中等分辨率的卫星遥感在大尺度范围上反演表层土壤水分和盐分的能力较为有限。如张智韬等[9]利用GF-1卫星遥感反演沙壕渠灌域农田表层土壤盐分,其构建的反演模型的精度R2在0.14～0.31之间。姚一飞等[17]利用GF-1卫星遥感对河套灌区不同土层深度农田土壤水分进行了反演,反演模型的R2大多位于0.4上下,部分深度反演模型的最大R2为采用机器学习算法构建所得,R2达到0.5左右,RMSE在0.025%上下。而本研究通过采用重采样和TsHARP升尺度法将无人机遥感数据上推以修正GF-1卫星遥感数据,构建不同土壤深度下无人机-卫星升尺度土壤水分反演模型,显著提高了卫星遥感在大尺度范围上对地表表层土壤水分的反演精度。其中,在TsHARP升尺度法中,相对基于传统的多元线性回归算法,将目前应用广泛的BP神经网络和支持向量机两种机器学习算法进行趋势面的构造,不同深度反演模型的R2整体由0.4提高至0.7以上,RMSE整体由0.025%降低至0.015%,大幅度提高了GF-1卫星对表层土壤水分的监测精度。由此可见,通过采用较低成本的无人机遥感工具辅助协同卫星遥感并进行合理的尺度转换,能有效提高卫星遥感在大尺度上对地表地物信息的监测,从而解决单一卫星遥感在大尺度范围监测地物信息精度不高的问题,具有一定的研究意义和实际应用价值。

本研究中,土壤深度0～60 cm和0～40 cm下的反演效果整体优于其它3种深度,其中0～60 cm略优于0～40 cm,深度0～20 cm和20～40 cm次之,深度40～60 cm反演效果最差,其原因主要是7月末为作物(葵花、玉米等)苗期结束、拔节期伊始时节,作物的大部分根系已向下伸展至深度60 cm,此时作物根系主要在距地表土壤深度0～50 cm下进行水分的吸收[31],在深度0～40 cm和0～60 cm处的根系对土壤水分更为敏感[32],从而表现出最佳的反演效果;而0～20 cm浅表层处的土壤水分容易受到太阳辐射、降水、风速等外界自然条件变化影响,在短时间内土壤水分难以维持一个相对稳定的状态,其在土壤样本采集试验与卫星成像间隔期间土壤水分已发生了变化,一定程度上失去了影响成像时刻的真实土壤水分。如张智韬等[33]基于TM5和TM7数据,采用归一化土壤湿度指数监测宝鸡峡二支渠灌区不同深度土壤含水率,得出的最佳监测深度为0～40 cm和0～60 cm,优于0～20 cm和0～10 cm;屈创[34]基于LandsatETM+和ASTER两种不同遥感数据,采用温度植被干旱指数法反演白龙江流域不同深度土壤水分,也得出深度0～40 cm和0～60 cm的反演精度高于0～20 cm的结论(野外实测土壤水分时间和卫星成像时刻间隔7 d);姚一飞等[17]基于GF-1卫星遥感对河套灌区不同土层深度农田土壤水分进行反演,同样得到土壤深度0～40 cm和0～60 cm的反演效果优于浅层 0～20 cm 的相似结论(野外实测土壤水分与卫星成像时刻存在间隔)。因此,在今后的研究中应尽量保证野外实测资料与遥感影像成像时间的同步,以减少影像成像时刻土壤含水率的真值丢失,从而提高浅层土壤水分的反演精度。

本研究仍存在一些不足,需要进一步深入探索。如光谱指数的选择是否最佳以及未采用另一种或多种变量筛选方法进行对比,所得的各深度最优变量组合实际上未必最优。此外,所建模型算法也仅是对波段及光谱指数与土壤含水率之间进行数量上的相关统计分析,这两者之间是否存在其它内在机理等联系仍有待探索[35],未来可着重在这方面上进行深入研究。内蒙古河套灌区作为本文的研究区,土壤盐渍化问题较为突出,而水分中常常含有各种盐分,且二者之间的运移[36-37]、交互等作用复杂[38],需要从物理学、化学机制以及数学模型等进一步分析盐分的影响并采取合理的方法进行剔除,故本研究所得结论的普适性还有待进一步探索。重采样和TsHARP升尺度法各有其特点和优势,未来可根据实际情况考虑将两种升尺度方法结合,以实现更为全面、合理的升尺度研究。

4 结论

(1)基于两种升尺度方法下的各深度MLR、BPNN和SVM模型的R2均较修正前较明显提高,各模型的RMSE均对应升尺度修正前明显降低。其中,重采样升尺度法在土壤深度0～60 cm下采用SVM模型最优,R2达到0.571,RMSE为0.022%;TsHARP升尺度法在土壤深度0～60 cm下采用BPNN模型最优,R2达到0.829,RMSE为0.015%。

(2)重采样升尺度法在不同土壤深度下模型整体精度由高到低依次为SVM模型、MLR模型、BPNN模型,TsHARP升尺度法在不同土壤深度下模型整体精度由高到低依次为BPNN模型、SVM模型、MLR模型,5种不同深度土壤下反演效果由高到低依次为0～60 cm、0～40 cm、0～20 cm、20～40 cm、40～60 cm。

(3)与升尺度修正前对应土壤深度模型对比,两种升尺度方法均能明显提高卫星遥感对土壤含水率的反演精度,但TsHARP升尺度法整体优于重采样法;重采样法的R2由0.413提升至0.571,RMSE由0.026%降至0.022%(降幅15.4%);TsHARP升尺度法的R2由0.428提升至0.829,RMSE由0.025%降至0.015%(降幅40.0%)。