除草机器人自适应快速积分终端滑模跟踪控制技术

冀 杰 贺 庆 赵立军,2 李 平 刘 洋 王小康

(1.西南大学工程技术学院, 重庆 404100; 2.重庆文理学院智能制造工程学院, 重庆 402160;3.重庆市农业科学院农业机械研究所, 重庆 404100)

0 引言

由于电动智能除草机器人在节省劳动力和环境保护方面优势明显,它已成为绿色智能农业机械发展的重要体现,受到越来越多研究机构和科研人员的重视[1]。路径跟踪控制是智能农机的关键技术之一,对于提高除草机器人作业效率和作业质量起到决定性的作用。而除草机器人在作业时往往受到系统内部参数摄动、未建模误差以及未知外部干扰等不确定因素的影响,难以快速准确地跟踪期望路径。因此,有必要为除草机器人设计一种响应快速、精度高、鲁棒性强并具有自适应能力的路径跟踪控制器。

近年来,各国学者设计了不同的控制器用于解决路径跟踪问题,例如自适应控制[2-4]、滑模控制[5-7]、神经网络控制[8-9]、H∞控制[10]等。其中,滑模控制具有快速响应、鲁棒性强等优点,被越来越多地应用到智能农机、智能车辆的路径跟踪中。针对非完整系统的动力学模型,文献[11]提出了基于反演技术的自适应滑模控制,该控制器能够使系统具有全局稳定性和较强的鲁棒性, 但需要准确获得集中扰动的上界信息,这在实际应用中难以实现。为此,文献[12]在跟踪控制器中增加了干扰观测器和自适应补偿器,用于处理系统不确定性和外界干扰。而在文献[13]设计的自适应滑模动态控制器中,引入了补偿外部扰动和动态不确定性的估计项,以及改善闭环稳定性、补偿外部扰动估计误差的反馈项。近年来,为了获得更快的响应速度,终端滑模控制逐渐被用于机器人系统中,它借助非线性超平面使跟踪误差在有限时间内收敛到零。文献[14]提出一种非奇异终端滑模(NTSM)控制,解决了普通终端滑模的奇异性问题。但控制器中的不连续到达控制会导致严重抖振。为克服控制信号的抖动,二阶滑模[15]、分数阶滑模[16]、递归滑模[17]等策略也被不断探索和应用。

由于除草机器人的动力学模型具有强非线性、使用环境具有强干扰的特点,为了有针对性地解决轨迹跟踪中的响应性、跟踪性及鲁棒性问题,基于上述分析,本文设计一种自适应快速积分终端滑模控制器。首先,考虑驱动轮动力学特性以及未建模误差、外界干扰、动静摩擦等不确定性因素,建立除草机器人的动力学模型。然后,基于所建立的动力学模型,设计带积分元素的快速终端滑模控制器,对滑模函数的控制参数进行自适应调整,从而适度减弱抖振,并且,通过嵌入自适应估计律,在不明确系统不确定性和干扰的情况下实现前馈补偿。最后,通过仿真对比和实地试验来验证所设计控制器在快速响应、高精度和强鲁棒性方面的性能。

1 除草机器人动力学建模

图1是自主设计的除草机器人模型俯视图,运动系统由两个驱动后轮和两个万向前轮组成,利用两后轮差速驱动实现除草机器人的运动控制。图中OXY表示全局坐标系,Gxy表示除草机器人局部坐标系。点G表示两后轮轴中心点位置,点Z为除草机器人质心位置。质心点Z的位姿q(xZ,yZ,θ)表示除草机器人在全局坐标系下的位姿。2a为两后轮中心之间的距离,b为点Z与点G之间的距离,两后轮半径为r。

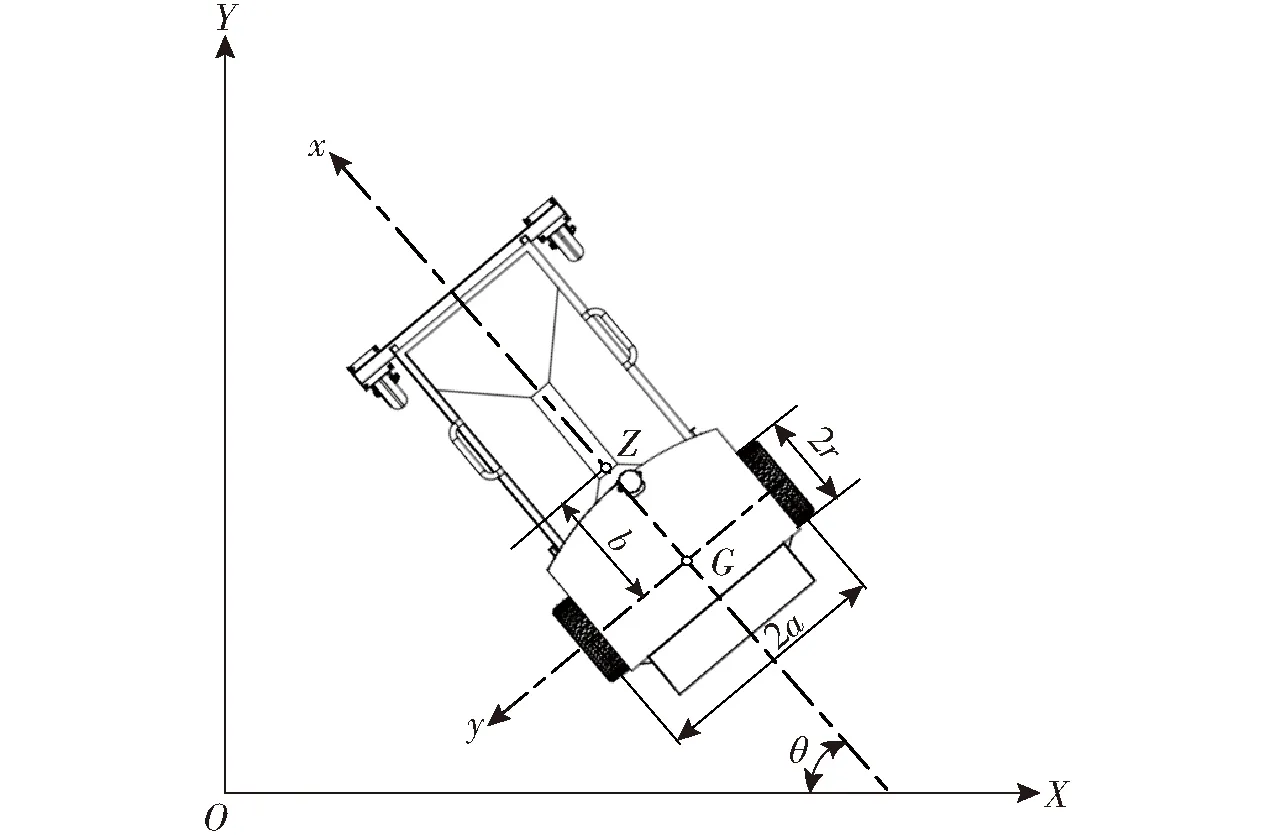
图1 除草机器人模型俯视图Fig.1 Top view of weeding robot model

除草机器人的运动学模型为

(1)

式中v——除草机器人点G线速度,m/s

w——除草机器人点G角速度,rad/s

B——运动学变换矩阵

u——速度向量

除草机器人为典型的非完整约束、非线性动力学系统,它在运动过程中始终满足约束方程

(2)

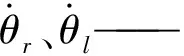
本文所设计的除草机器人采用机械链条传动,并假定驱动轮始终做无滑动的纯滚动运动,通过对两驱动轮进行动力学分析,得到

(3)

式中Iw——左、右后轮的转动惯量,kg·m2

τr、τl——左、右电机的驱动力矩,N·m

Fr、Fl——左、右轮的驱动力,N

μw——电机与传动机构之间的粘性摩擦因数

针对质心点Z,建立除草机器人本体的牛顿欧拉方程,得到动力学方程

(4)

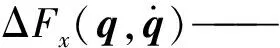
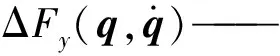
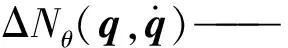
IZ——割草机质心的转动惯量,kg·m2

λ——拉格朗日乘子

m——除草机器人质量

对运动学方程(1)、约束方程(2)、驱动轮动力学方程(3)以及除草机器人动力学方程(4)进行联立求解,得到除草机器人的完整动力学模型

(5)

其中

(6)

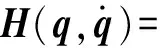
(7)

(8)

(9)

(10)

式中M(q)——惯性力矩阵

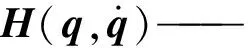
A(q)——非完整约束矩阵

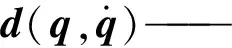
S(q)——输入变换矩阵

τ——驱动力矩向量

式(5)两边同时乘以BT(q),消除其中的约束项A(q)λ,并代入式(1),则受非完整约束的除草机器人动力学方程可简化为

(11)

其中

2 除草机器人控制系统设计

2.1 控制系统结构

除草机器人的整体控制系统如图2所示,由基于运动学模型的速度控制器和基于动力学模型的轨迹跟踪滑模控制器共同组成。根据除草机器人实际位姿q=(xZ,yZ,θZ)T与参考位姿qr=(xr,yr,θr)T产生虚拟的期望速度ud=(vd,wd)T,其中,参数观测器用于估计除草机器人质心点Z与两后轮中心点G的距离b。然后,利用设计的滑模控制器产生控制转矩,从而使除草机器人的实际速度u能够跟踪虚拟速度ud,同时,利用自适应估计律补偿外界干扰和系统不确定性。

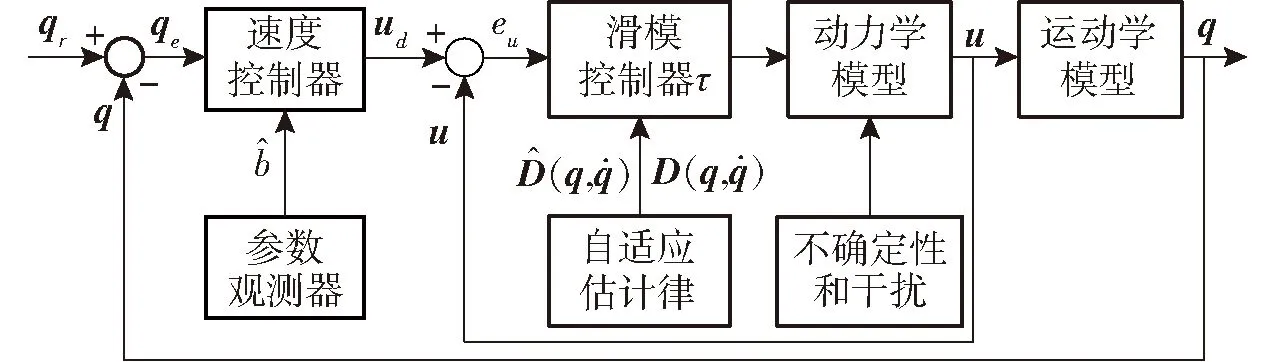
图2 控制系统结构框图Fig.2 Block diagram of control system

2.2 速度控制器设计

2.2.1速度控制律推导

如前所述,速度控制器的目标是生成虚拟期望速度ud,从而使除草机器人的实际位姿与参考位姿的跟踪误差收敛到零。根据文献[18]定义除草机器人的轨迹跟踪误差qe为

(12)

对式(12)进行求导得到

(13)

为了有效消除机器人的轨迹跟踪误差,定义除草机器人轨迹跟踪误差qe的李雅普诺夫函数为

(14)

kθ——正常数

对式(14)进行求导得出

(15)

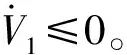
(16)

式中kx(vr,wr)、ky(vr,wr)——与角速度和线速度参考值相关的有界非线性连续函数

运动学模型参数b的自适应律表示为

(17)

2.2.2稳定性分析

速度控制器是基于李雅普诺夫函数而设计的,需要引入以下假设和Barbalat引理以及推论来作为证明控制器稳定性的前提。

假设:参考线速度和参考角速度以及它们的导数都是有界的。在任意时间内满足

(18)

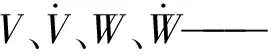
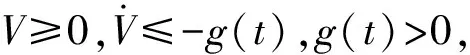
将式(16)、(17)代入式(15)得到

(19)

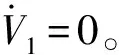
(20)

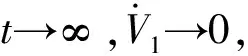
(21)

对式(21)求导可得

(22)

2.3 滑模控制器设计

2.3.1滑模控制律推导

在不确定性或外部干扰的情况下,滑模控制系统的输出u=(v,w)T要能够有效跟踪虚拟速度ud=(vd,wd)T。为了实现这一目标,需要进行以下合理假设:不确定性和外界干扰是有界的,并且满足关系[20]

(23)

式中η1、η2、η3——未知有界的正数

在不考虑干扰和不确定性的情况下,式(11)变为

(24)

速度跟踪误差表示为

(25)

为了在系统不确定性和外界干扰的影响下,消除稳态误差,并在有限时间内迅速收敛到平衡状态,滑模面引入积分元素和非线性函数sigφ(x),即

(26)

式中α1、α2——滑模函数参数,α1>0、α2>0

φ——非线性函数参数,0<φ<1

对于β>0,∀x∈R,sigφ(x)是一个单调递增的平滑函数[21],定义为

sigφ(x)=|x|φsgn(x)

(27)

式中 sgn(x)——符号函数

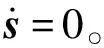
(28)

所以等效控制律为

(29)

在考虑干扰和不确定性的情况下,为保证系统的状态不离开滑模面,设计切换控制律

(30)

式中ξ1、ξ2——控制参数,ξ1>0、ξ2>0

δ——控制参数,δ>1

(31)

式中σ1、σ2、σ3——自适应律增益参数,σ1>0、σ2>0、σ3>0

将式(29)与式(30)相加即可得到滑模控制律,即

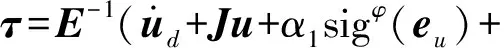
(32)

2.3.2稳定性分析

为分析滑模控制器的稳定性,定义李雅普诺夫函数

(33)

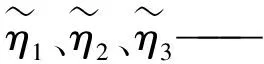
对式(33)微分得

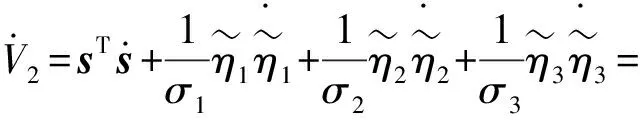
(34)

由式(13)、(28)、(32)得到

(35)

假设s(t=0)≠0,由式(31)可知1、2、3是单调递增的,所以存在一个有限的时间T1使得

(36)

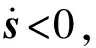
(37)

其中

Ψ=min(Γs,Γ1,Γ2,Γ3)

(38)

假设V2(0)≠0到V2(tr)=0的时间为tr。由式(37)可得

(39)

所以,在任意初始条件V2(0)下,存在有限的时间tr使得V2→0,即s→0。当系统处于滑动模态时(s=0)有

(40)

根据式(40)可得

(41)

设初始时刻的误差为eu(0),求解微分方程式(41)得到

(42)

设t=ts时,eu=0,则由式(42)可求解出ts为

(43)

因此,当式(26)中的s为0时,即系统处于滑动模态时,在任何初始条件eu(0)下,误差eu将在有限的时间ts内收敛到0。

2.4 控制器参数优化

在实际应用中,由于噪声和切换延迟,滑模变量s可能存在抖振的情况,i会一直增加并造成控制输入过大。因此,本研究通过使用死区的方法来缓解这个问题[22]。式(31)变为

(44)

式中ρ——较小的正常数

(45)

式中ι——边界层,ι>0

减小式(26)中的参数φ,可提高系统响应速度,但会增大系统抖振,甚至使系统发散。所以,理想的φ应该是时变的,即随着误差的减少而增大。因此,设计φ与eu的经验函数

φ=e-(λ|eu|+0.5)γ+0.2

(46)

式中λ、γ——正常数

3 仿真分析

为测试控制算法的有效性,在Matlab软件中对其进行仿真验证,并与文献[13]所提出的自适应滑模动态控制器(Adaptive sliding mode dynamic controller, ASMDC)、文献[24]提出的双环姿态跟踪鲁棒控制器(Double ring attitude tracking robust controller, DRATRC)、文献[11]提出的自适应滑模控制器(Adaptive sliding mode controller, ASMC)进行对比。仿真分析采用的除草机器人物理参数以及控制器仿真参数如表1、2所示,除草机器人的初始位姿为:xZ=-1 m,yZ=-1 m,θZ=0 rad。

表1 除草机器人参数Tab.1 Parameters of weeding robot

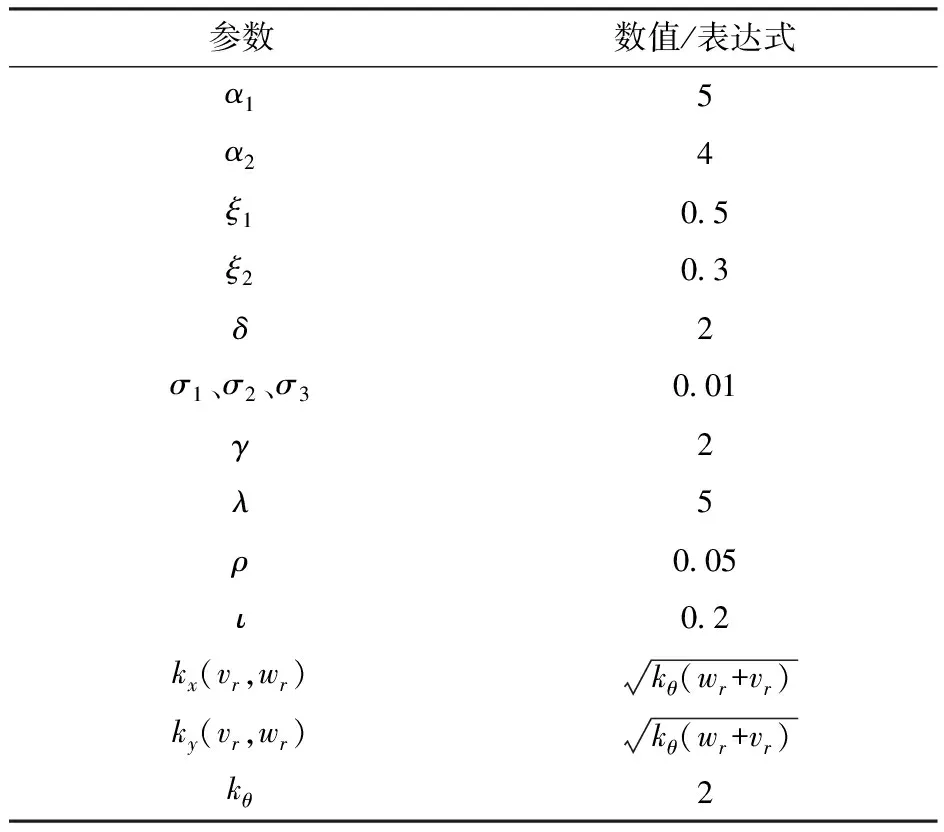
表2 控制器仿真参数Tab.2 Simulation parameters of controller

除草机器人在纵向、横向和航向上受到系统不确定性和外界干扰造成的合力设置为

(47)

仿真结果如图3所示。从图3a可以看出,当除草机器人的初始位置与期望路径存在一定的差距时,4种算法均能使机器人较为快速地逼近期望路径,并在随后的运动中实现较好的轨迹跟踪效果。图3b显示了除草机器人在横向、纵向和航向角上的跟踪误差,比较本文所设计的自适应快速积分终端滑模控制器(AFITSMC)与另外3种控制器的跟踪误差可以看出,4种控制器的控制效果存在一定的差异。4种控制器在3个方向上的初始误差分别是1 m、1 m、0 rad,采用ASMDC、DRATRC和ASMC控制器时,除草机器人的3种误差约13 s之后会渐近逼近零,振荡收敛。位置稳态误差在-0.05～0.05 m之间波动,而航向角的稳态误差在-0.1～0.1 rad之间波动。由于AFITSMC算法在滑模函数中引入了积分元素和非线性函数,所以,横向、纵向和航向角上的误差在有限时间约3 s内快速收敛到零,随后,稳态误差也收敛于零。可见,AFITSMC控制器的快速性和精确性优于另外3种控制器。并且,由图3c可以看出,自适应估计增益能够在有限时间内收敛到稳定状态。图3d显示了4种控制器的线速度与角速度的跟踪曲线,与另外3种控制器相比,本文提出的AFITSMC控制器能够使机器人迅速达到期望的线速度和角速度,并最终稳定收敛到期望值。但是,由于AFITSMC控制器的快速跟踪特性,线速度与角速度会在起始阶段存在短时间的速度突变。从图3e可以看出,在模型不确定性和外界干扰的影响下,采用ASMDC控制器和ASMC控制器时,两驱动电机的输入力矩在短时间内会有较大的波动,容易造成除草机器人抖振,不利于除草机器人作业。而采用DRATRC控制器和AFITSMC控制器时,输入力矩曲线较为平滑,有效降低了系统的抖振。另外,除草机器人的输入力矩在初始时有比较明显跳变,这是由于除草机器人的起始位置与参考轨迹的起始位置有比较大的误差,需要较大的控制力矩使得系统迅速达到平衡状态。因此,在实际轨迹跟踪时,可以适当减小起始误差和相应的控制增益,以减小在启动阶段的力矩跳变。

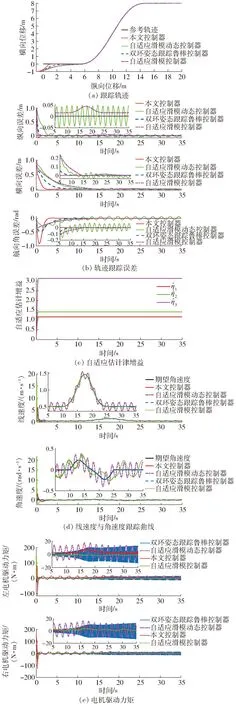
图3 除草机器人仿真结果Fig.3 Simulation results of weeding robot

综上可知,在系统不确定性和外界干扰的影响下,本文所设计的AFITSMC控制器与ASMDC控制器、DRATRC控制器、ASMC控制器相比,具备一定的抗抖振能力和鲁棒性,并在有限时间内能使跟踪误差快速收敛到零,具有更好的跟踪性能。

4 试验验证

4.1 试验平台

为进一步验证提出的控制算法的有效性,在如图4所示的自主设计的除草机器人平台上进行试验验证,具体结构参数见表1。除草机器人平台上配备了英伟达Jetson Agx Xavier控制器、Velodyne 16线激光雷达、惯性测量单元(IMU)、额定功率2 000 W和额定转速100 r/min的科亚直流伺服电机及其驱动器、48 V蓄电池等硬件。主机的操作环境为Ubuntu 18.04系统,机器人操作系统为ROS 1,通过C++语言在ROS 1上编写本文控制算法节点、路径规划节点和SLAM节点来实现除草机器人的跟踪控制。基于激光雷达和IMU传感器的融合数据,SLAM节点实时发布除草机器人的位姿信息、线速度及角速度信息到控制算法节点,本文采用文献[25]提出的 LeGO-LOAM算法作为机器人的SLAM算法。控制算法节点通过从路径规划节点获取参考路径信息。最后,通过科亚直流伺服电机驱动器的串口协议,向左、右后轮驱动电机发送控制力矩指令,最终实现除草机器人的轨迹跟踪控制。

图4 除草机器人平台Fig.4 Weeding robot platform1.惯性测量单元 2.割刀电机驱动器 3.后轮电机驱动器 4.电源 5.Velodyne 16激光雷达 6.Jetson Agx Xavier控制器 7.左右后轮驱动电机

4.2 除草机器人作业试验

试验场地选择重庆市农业科学院的闲置地块,该地块起伏不平且杂草的平均高度约为32 cm,除草机器人在作业行驶时会受到随机干扰,试验现场如图5所示。除草机器人在草坪上的作业路径主要包括直线行驶以及掉头转向,因此,以S形路径作为目标轨迹进行跟踪测试。根据除草机器人结构尺寸和试验场地环境,实际目标路径如图6a中黑色曲线所示。由于使用激光雷达和IMU传感器获取除草机器人的里程计信息,因此,除草机器人在初始时刻的位姿为(0 m,0 m,0 rad);而规划路径的起始点位姿为(1 m,1 m,0 rad),初始时刻的横向误差、纵向误差、航向角误差分别为1 m、1 m、0 rad。

图5 试验场景Fig.5 Scenario for experiment

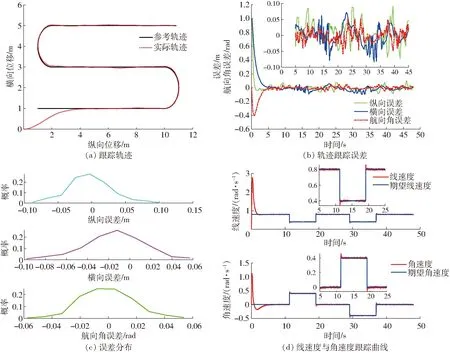
图6 试验结果Fig.6 Experimental results

从图6a、6b可以看出:在初始时刻,除草机器人的横向偏差和纵向偏差大约在5 s内都能迅速收敛到零附近,证明提出的控制算法能够保证除草机器人的跟踪误差在有限时间内迅速收敛。而在稳态轨迹跟踪过程中,除草机器人的横向误差、纵向误差和航向角误差的统计如表3所示,横向、纵向、航向角误差总体最大绝对值分别为0.097 9 m、0.102 6 m、0.057 8 rad,而最小绝对值为0.000 1 m、0.000 1 m、0.000 1 rad,平均绝对值分别为0.015 6 m、0.015 5 m、0.008 6 rad,均方差分别为0.019 5 m、0.019 7 m、0.011 1 rad。数据表明:即使存在模型不确定和外界干扰的情况下,本文提出的控制算法能够使除草机器人较为快速且平滑地跟踪目标轨迹,将误差控制在较小范围内,有效保证了跟踪效果。从图6c所示的横向、纵向、航向角误差的概率分布图也能看出,3个方向上的误差近似服从以零为均值的正态分布,误差大概率集中在-0.05～0.05区间内,波动幅度较小。对除草机器人的感知及执行机构进行分析,得出造成机器人在3个方向上产生误差波动的2个主要原因:激光雷达和IMU传感器存在一定噪声且精度不足;执行电机控制存在时间滞后,导致除草机器人在获取定位时的位姿信息和速度信息不够精确,且力矩执行不够及时。因此,与主机发出的规划、定位、控制信号相比,执行机构存在不可避免的延迟和误差。从图6d可以看出,线速度和角速度也能实现较好的跟踪效果。在初始时刻,由于除草机器人位姿与参考位姿有较大的误差,为了迅速使误差得到收敛,机器人需要产生较大的瞬时线速度和角速度,从而很快收敛到期望速度。在11、19、29、36 s时刻,由于曲率的突变,跟踪的线速度与角速度会产生一个较小的突变,这是由于路径规划时速度不平滑导致的。在其他时间内,除草机器人的线速度和角速度无明显抖动,表明本文提出的控制算法能够有效抑制除草机器人在轨迹跟踪过程中的抖振。

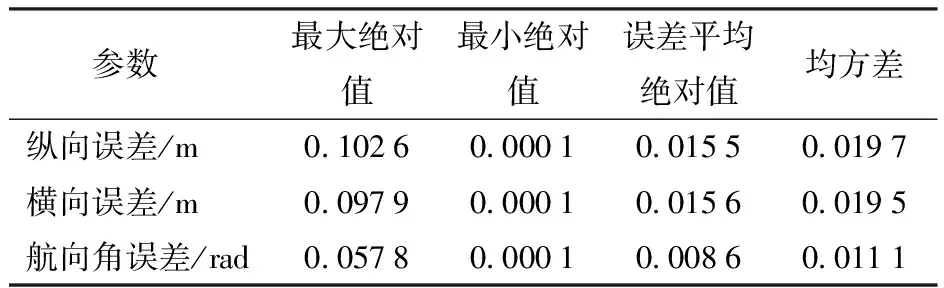
表3 跟踪误差统计结果Tab.3 Statistical results of tracking errors

从轨迹跟踪试验结果可知,设计的控制器在控制精度和稳定性方面都能满足除草机器人的作业要求,并且,系统在受到参数摄动和外界干扰时,控制器能有效抑制干扰造成的抖振,具有较强的鲁棒性和快速收敛性。

5 结论

(1)针对除草机器人易受到外部干扰和自身不确定性的特点,建立了考虑驱动轮动力学特性以及未建模误差、外界干扰、摩擦变化等不确定性因素的除草机器人动力学模型。

(2)基于自适应控制和终端滑模控制设计了除草机器人的轨迹跟踪控制方法,能够保证除草机器人在有限时间内迅速跟踪期望轨迹。此外,所提出的自适应律可以在线估计未知扰动,从而提高了扰动抑制性能,显著缓和了控制抖振。

(3)提出的方法能够使姿态跟踪误差在短时间内收敛到零,并且控制器参数不需要明确的扰动上界,实际应用中具有普适性。

(4)仿真与试验结果表明,所设计的跟踪控制算法能够使除草机器人在真实作业环境中具有高跟踪精度、快速响应和很强的抗干扰性能。