无纺布的粘弹性泊松比
夏腾腾 葛陈勇 李健 李红光 李勇

摘要:为了研究无纺布的粘弹性力学行为,精确计算其粘弹性泊松比。以粘弹性力学理论为基础,结合Laplace变换和蠕变应力条件,推导了由横向应变和松弛模量计算粘弹性泊松比的精确表达式。由蠕变实验和松弛实验数据,获得了无纺布横向应变和松弛模量随时间变化的Prony级数,并利用1stOpt软件模拟了无纺布的粘弹性泊松比时变曲线。结果表明:在蠕变条件下,随着载荷作用时间增加,无纺布泊松比逐渐增大并趋近于0.25。该方法可有效获得无纺布的粘弹性泊松比,为其后续生產加工所涉及的力学指标计算提供参考值。
关键词:无纺布;泊松比;粘弹性;蠕变;松弛
中图分类号:TS171
文献标志码:A
文章编号:1009-265X(2023)02-0107-05
泊松比是衡量材料力学性能的重要指标之一,其精确表达和测定对相关研究工作极为重要[1-2]。部分学者对针织物、机织物、无纺布等的泊松比做了研究[3-5],但多将织物作为弹性材料考虑,即认为泊松比为常数。粘弹性材料的泊松比一般表现出与温度和时间的相关性,若假定为常数,会使得其相关应力分析和强度计算产生较大误差[6]。随着纺织产业发展,无纺布产量和使用量逐年增加,对于无纺布力学性能的研究也逐渐被重视。通过拉伸测试发现,无纺布具有典型的粘弹性属性。作为材料的基本力学参数之一,无纺布粘弹性泊松比的精确测定必不可少。
目前,关于材料粘弹性泊松比的研究较多,但针对纺织材料的研究尚未见到。Lakes等[7]对线性粘弹性固体中的泊松比进行了理论分析,发现粘弹性泊松比与加载时间呈函数关系,但并不一定随时间单调增大。郑健等[8]采用遗传积分形式表达粘弹性泊松比,结合蠕变实验条件,推导并计算了固体推进剂的粘弹性泊松比。申志彬等[9]提出了一种基于数字图像法的固体推进剂泊松比高精度测量方法,研制相应的测试系统并测定了HTPB推进剂的粘弹性泊松比。Hoshino 等[6]提出利用二维数字图像法直接测量动态粘弹性实验中的泊松比的方法,并通过测试环氧树脂的材料特性进行了验证。
基于粘弹性力学理论,本文建立了粘弹性泊松比表达式,结合蠕变实验和松弛实验测定材料拉伸指标,精确计算了无纺布粘弹性泊松比,以期为纺织材料的泊松比测定提供参考。
1粘弹性泊松比计算
常规弹性泊松比v定义为:
v=-εx/εy(1)
式中:εx为材料横向应变;εy为材料纵向应变。
无纺布具有典型的粘弹性属性,在载荷作用下会产生松弛或蠕变,且横向应变响应εx(t)滞后于纵向变形历史εy(t) [10-11]。因此,直接由拉伸过程实测值εx(t)、εy(t)计算,无法得到精确泊松比v(t)。
基于弹性-粘弹性对应原理,在恒定载荷拉伸作用下,粘弹性时域泊松比v(t)为:
v(t)=-εx(t)/εy(t)(2)
粘弹性泊松比v(t),表征在拉伸静载作用下横向应变εx(t)对纵向应变εy(t)的响应,是横向变形的一个记忆函数[12]。
对于线性粘弹性材料,定义Laplace变换域内的泊松比v(s)为:
v(s)=-εx(s)/εy(s)(3)
式中:纵向应变εy(s)=σy(s)/E(s);蠕变实验中,纵向拉伸应力σy(s)=σ0/s;符号上的“-”表示Laplace变换算符。
则式(3)可写为:
v(s)=-εx(s)sE(s)/σ0(4)
式中:σ0为蠕变拉伸应力;E为拉伸松弛模量。
利用卷积定理,对式(4)求Laplace逆变换,得:
v(t)=-1σ0∫t0E(t-τ)εx(τ)dτ(5)
利用式(5),可由εx(t)和E(t)的实验值求得粘弹性泊松比v(t)的精确值,是间接测试粘弹性泊松比的理论基础。
令εx(t)、E(t)为Prony级数形式,如下:
εx(t)=εxe+∑mi=1εxiexp(-t/τi)
E(t)=Ee+∑nj=1Ejexp(-t/τj)(6)
式中:m、n为Prony级数的阶数;εxe为最终应变;εxi为各阶应变量;τi为各阶蠕变时间;Ee为平衡模量;Ej为各阶松弛模量;τj为各阶松弛时间。
将式(6)代入式(5)并整理,即得材料蠕变的粘弹性泊松比精确表达式:
v(t)=-1σ0[Ee∑mi=1εxi(exp(-t/τi)-1)+
∑mi=1∑nj=1εxiEjτjτj-τi(exp(-t/τi))-exp(-t/τj))](7)
2实验
2.1实验材料
本研究选用佳联达无纺布有限公司生产的聚丙烯(PP)熔喷无纺布(以下简称无纺布),纤维间接触形式为点粘合,幅宽143 mm、厚度0.305 mm、平方米质量30 g/m2。
考虑试样厚度较小,忽略无纺布厚度方向应力及应变分量,仅讨论无纺布的二维平面泊松比[4]。因所选无纺布内部纤维不存在经纬取向,本文认定其为平面各向同性材料。
参考标准GB/T 24218.3—2010《纺织品 非织造布试验方法 第3部分:断裂强力和断裂伸长率的测定(条样法)》,并根据实际情况进行相关实验设置。
2.2蠕变实验
试样上下端用夹具夹持,悬挂并施加纵向载荷。试样尺寸为300 mm×70 mm,夹持距离200 mm。为避免卷边影响,测量位置距边缘10 mm,即测量宽度为50 mm。为使无纺布不发生结构破坏且横向应变可测量,确定纵向载荷为0.239 MPa(由下端夹具和砝码共同施加,夹具20.7 g,砝码500 g),载荷瞬时施加并持续12 h。实验示意如图1(a)所示。测量并记录试样中部最窄处的宽度随蠕变时间变化情况,进行5次实验并取平均值,计算得到布料中部横向应变εx′。考虑布料在较小载荷作用下存在轻微颈缩现象,以0.5εx′作为等效横向应变εx,得到εx-t曲线。
2.3松弛实验
仪器设备采用YT010-1000型土工布综合强力试验机,试样尺寸为300 mm×50 mm,夹持距离200 mm。本实验数据处理采用基于Prony级数的数据拟合法[13],该方法综合考虑了松弛实验加载阶段和松弛阶段,初始应变和加载速度对计算结果无影响,考虑实验效率且避免冲击载荷,确定拉伸速度20 mm/min。考虑无纺布不发生结构破坏且应力可测量,拉伸试样至0.05纵向应变后停止,保持拉伸状态12 h。实验示意如图1(b)所示。记录拉力值随松弛时间变化情况,进行5次实验并取平均值,计算拉伸应力σ,得到σ-t曲线。
3结果与分析
3.1蠕变实验结果
通过蠕变实验,得到无纺布蠕变过程等效横向应变随时间变化关系,如图2所示。
由图2可知,载荷施加瞬间,试样产生约0.023的等效横向应变,该阶段应变主要由纤维及纤维网的弹性变形引起。其后,随着蠕变时间的增加,横向应变逐渐增大并趋近于定值,该阶段应变归因于无纺布内部纤维间的粘结点逐步剥离和滑移。
采用Levenberg-Marquardt优化算法[14],拟合蠕变阶段(瞬时应变之后)实验曲线,得到无纺布等效横向应变εx(t)的6阶Prony级数表达式:
εx(t)=εxe+∑m=6i=1εxiexp(-t/τi)=-0.03491+
0.00202e-t/11759.96575+0.007e-t/11031.19268+
0.00183e-t/204.64279+0.00012e-t/444.43763+
0.00077e-t/30.03434+0.00013e-t/0.10405
(8)
3.2松弛实验结果
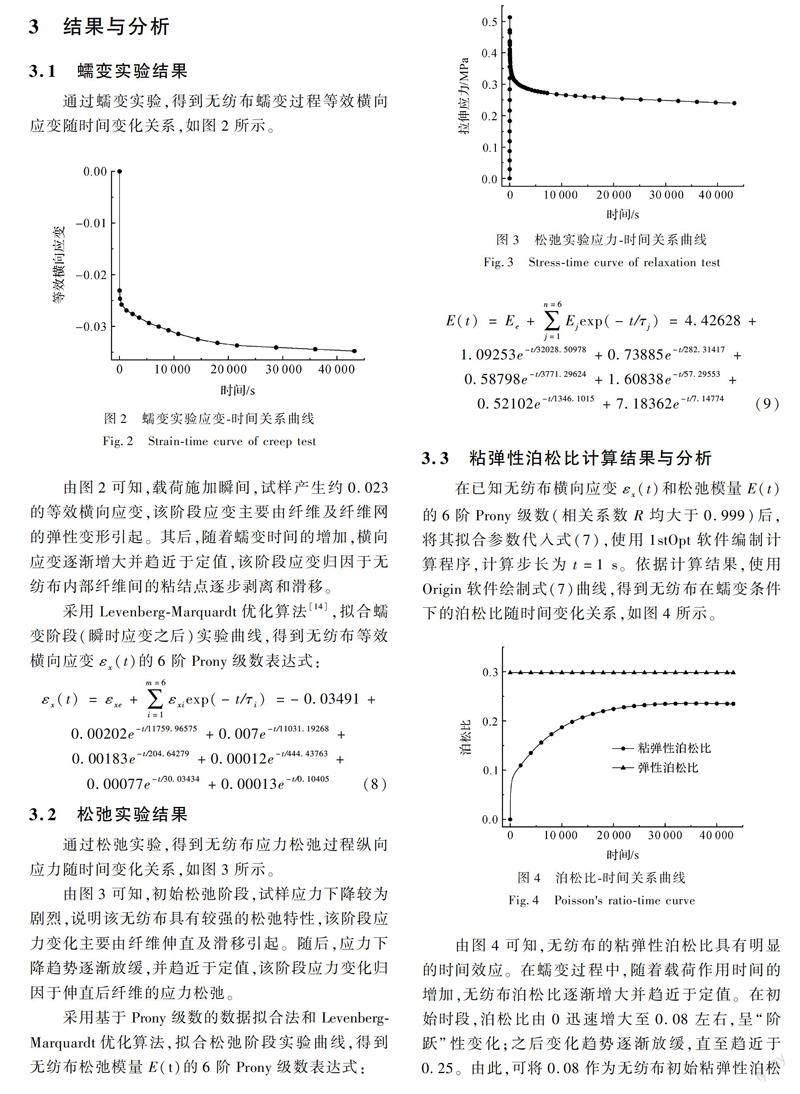
通过松弛实验,得到无纺布应力松弛过程纵向应力随时间变化关系,如图3所示。
由图3可知,初始松弛阶段,试样应力下降较为剧烈,说明该无纺布具有较强的松弛特性,该阶段应力变化主要由纤维伸直及滑移引起。随后,应力下降趋势逐渐放缓,并趋近于定值,该阶段应力变化归因于伸直后纤维的应力松弛。
采用基于Prony级数的数据拟合法和Levenberg-Marquardt优化算法,拟合松弛阶段实验曲线,得到无纺布松弛模量E(t)的6阶Prony级数表达式:
E(t)=Ee+∑n=6j=1Ejexp(-t/τj)=4.42628+
1.09253e-t/32028.50978+0.73885e-t/282.31417+
0.58798e-t/3771.29624+1.60838e-t/57.29553+
0.52102e-t/1346.1015+7.18362e-t/7.14774
(9)
3.3粘弹性泊松比计算结果与分析
在已知无纺布横向应变εx(t)和松弛模量E(t)的6阶Prony级数(相关系数R均大于0.999)后,将其拟合参数代入式(7),使用1stOpt软件编制计算程序,计算步长为t=1 s。依据计算结果,使用Origin软件绘制式(7)曲线,得到无纺布在蠕变条件下的泊松比随时间变化关系,如图4所示。
由图4可知,无纺布的粘弹性泊松比具有明显的时间效应。在蠕变过程中,随着载荷作用时间的增加,无纺布泊松比逐渐增大并趋近于定值。在初始时段,泊松比由0迅速增大至0.08左右,呈“阶跃”性变化;之后变化趋势逐渐放缓,直至趋近于0.25。由此,可将0.08作为无纺布初始粘弹性泊松比,则泊松比为随时间从0.08逐渐趋近于0.25的值。本文所得无纺布粘弹性泊松比在正常泊松比范围(0~0.5)内,且符合绝大部分材料泊松比约为1/3的情况[15]。泊松比趋近值(v=0.25),与高晓平[3]所得聚丙烯热粘合无纺布(点粘合)弹性泊松比结果相近,存在差异可能是由于布料规格、生产工艺等不同,但仍具有一定参考价值。
4结论
粘弹性材料泊松比不能简单假定为常数,而是一个与时间相关的函数。基于无纺布的粘弹性属性,本文推导了横向应变εx(t)和松弛模量E(t)等效计算泊松比的方法。以Prony级数拟合蠕变实验和松弛实验数据得到εx(t)、E(t),再经1stOpt软件计算得到了无纺布泊松比与时间的关系,发现无纺布泊松比逐渐增大并趋近于0.25。所得结果符合常规泊松比范围,且与相关研究吻合较好。本文所述方法,可较为简便地计算无纺布等纺织材料的粘弹性泊松比,为其后续生产加工所涉及的力学指标计算提供参考值。
参考文献:
[1]MOTT P H, DORGAN J R, ROLAND C M. The bulk modulus and Poisson's ratio of "incompressible" materials[J]. Journal of Sound and Vibration, 2008, 312(4/5): 572-575.
[2]高光发,李永池,王道荣,等.多功能布泊松比的实验研究[J].力学与实践,2010,32(5):62-66.
GAO Guangfa, LI Yongchi, WANG Daorong, et al. Experi-mental study on Poisson's ratio of multi-function clothes[J]. Mechanics in Engineering, 2010, 32(5): 62-66.
[3]高曉平,宋钦杰.基于图像处理技术的非织造土工布的泊松比测试[J].产业用纺织品,2014,32(12):35-38.
GAO Xiaoping, SONG Qinjie. Measurement of Poisson's ratio of nonwoven geotextilebased on image processing tech-nology[J]. Technical Textiles, 2014, 32(12): 35-38.
[4]杨可,王朝晖.基于数字图像相关法的针织物泊松比测定[J].毛纺科技,2021,49(1):1-6.
YANG Ke, WANG Zhaohui. Measurement of Poisson's ratio of knitted fabrics based on digitalimage correlation method[J]. Wool Textile Journal, 2021, 49(1): 1-6.
[5]卢业虎,戴晓群.基于双向拉伸法的织物泊松比测定[J].纺织学报,2009,30(9):25-28.
LU Yehu, DAI Xiaoqun. Calculation of fabrics Poisson ratio based on biaxial extension[J]. Journal of Textile Research, 2009, 30(9): 25-28.
[6]HOSHINO Y, TAMAI K, ZHANG Y, et al. Direct measurement and master curve construction of viscoelastic Poisson's ratio with digital image correlation[J]. Strain, 2018, 54(6): e12294.
[7]LAKES R S, WINEMAN A. On Poisson's ratio in linearly viscoelastic solids[J]. Journal of Elasticity, 2006, 85(1): 45-63.
[8]郑健,张建彬,周长省,等.蠕变试验下固体推进剂泊松比研究[J].南京理工大学学报,2014,38(5):593-596.
ZHENG Jian, ZHANG Jianbin, ZHOU Changsheng, et al. Study on Poisson's ratio of solid propellant using creep test[J]. Journal of Nanjing University of Science and Technology, 2014, 38(5): 593-596.
[9]申志彬,邓斌,潘兵.推进剂粘弹性泊松比测试的数字图像相关方法[J].固体火箭技术,2016,39(4):513-518.
SHEN Zhibin, DENG Bin, PAN Bing. Digital image correlation method for measuringviscoelastic Poisson's ratio of propellant[J]. Journal of Solid Rocket Technology, 2016, 39(4): 513-518.
[10]单桂芳,杨伟,冯建民,等.材料泊松比测试方法的研究进展[J].材料导报,2006,20(3):15-20.
SHAN Guifang, YANG Wei, FENG Jianmin, et al. Advances in test methods for Poisson's ratio of materials[J]. Materials Reports, 2006,20(3): 15-20.
[11]李驭骉,李海滨.粘弹性药柱泊松比的实验研究[J].新型工业化,2016,6(4):16-21.
LI Yubiao, LI Haibin. Experimental Study on Poisson's ratio of viscoelastic grain[J]. The Journal of New Indus-trialization, 2016, 6(4): 16-21.
[12]赵伯华.粘弹性泊松比与动态复数泊松比的研究[J].推进技术,1995,16(3):1-7.
ZHAO Bohua. An investigation on viscoelastic Poisson's ratio and dynamic complex Poisson's ratio[J]. Journal of Propulsion Technology, 1995, 16(3): 1-7.
[13]许进升,鞠玉涛,郑健,等.复合固体推进剂松弛模量的获取方法[J].火炸药学报,2011,34(5):58-62.
XU Jinsheng, JU Yutao, ZHENG Jian, et al. Acquisition of the relaxation modulus of Composite solid propellant[J]. Chinese Journal of Explosives & Propellants, 2011, 34(5): 58-62.
[14]李虎,周国发.模内微装配成型二次充填熔体应力松弛特性研究[J].塑料工業,2019,47(11):59-62.
LI Hu, ZHOU Guofa. Study on stress relaxation characte-ristics of secondary injection meltfor in-micro mold assembly[J]. China Plastics Industry, 2019, 47(11): 59-62.
[15]ALDERSON K L, FITZGERALD A, EVANS K E. The strain dependent indentation resilience of auxetic microporous polyethylene[J]. Journal of Materials Science, 2000, 35(16): 4039-4047.
Viscoelastic Poisson's ratio of nonwovens
XIA Tengteng1,2, GE Chenyong3, LI Jian1,2, LI Hongguang4, LI Yong1,2
(1.The Mechanical Engineering College, Tarim University, Alaer 843300, China;
2.The Key Laboratory of Colleges & Universities under the Department of Education of Xinjiang Uygur Autonomous Region, Alaer 843300, China;
3.Alaer Fiber Inspection Institute, Alaer 843300, China;
4.Alar City Zhongtai Textile Technology Co., Ltd., Alaer 843300, China)
Abstract: The nonwoven is widely used in many industries and occupies a large proportion in the textile industry for its excellent performance, low cost and diversified types,. With the utilization of nonwovens in various industries, the output and usage have increased year by year. Therefore, in order to promote the use of nonwovens, it is necessary to study the mechanical properties of nonwovens. It can be found from the tensile test curve that all kinds of nonwovens have typical viscoelastic properties. Poisson's ratio, as one of the important indexes to measure the mechanical properties of materials, has been concerned and studied by many scholars, and some of them have studied the viscoelastic Poisson's ratio of materials. However, most studies focus on the viscoelastic Poisson's ratio of solid propellants, epoxy resins, and other materials. The research on textile materials has not been reported, but it has great research value.
The conventional polypropylene (PP) melt-blown nonwoven was selected as the object, the viscoelastic mechanical behavior of the nonwoven was tested, and its viscoelastic Poisson's ratio was accurately calculated. Based on the theory of viscoelastic mechanics, combined with Laplace transform and creep stress conditions, the exact expression of viscoelastic Poisson's ratio was calculated by transverse strain (under creep conditions) and relaxation modulus. The internal fibers of nonwovens are disordered and thin, so they can be regarded as isotropic materials (ignoring the stress and strain in the thickness direction), and only the two-dimensional planar Poisson's ratio is studied. The creep and relaxation experiments of nonwovens were carried out according to the standard GB/T 23218.3—2010, and the curves of transverse strain and relaxation modulus were obtained and fitted into the 6th-order Prony series. The Prony series of transverse strain and relaxation modulus were substituted into the expression of viscoelastic Poisson's ratio, and the time-varying curve of viscoelastic Poisson's ratio of nonwovens under creep condition was calculated by using 1stOpt software. In this study, the calculation method of viscoelastic Poisson's ratio was introduced into textile materials, and the viscoelastic Poisson's ratio of the selected nonwoven was analyzed and measured. It is found that as the loading time increases, the viscoelastic Poisson's ratio of the material gradually increases and tends to be constant. The viscoelastic Poisson's ratio approach value of the nonwoven selected in this paper is close to 0.25, which is in line with the Poisson's ratio range of conventional materials and is close to the value of conventional elastic Poisson's ratio in related research.
The method can effectively determine the viscoelastic Poisson's ratio of nonwovens, with simple operation and reliable results, which can provide reference for the determination of Poisson's ratio of other textile materials.. The accurate determination of viscoelastic Poisson's ratio also provides a reference value for the calculation of mechanical indexes involved in the subsequent production and processing of textile materials.
Keywords: nonwoven; Poisson's ratio; viscoelasticity; creep; relaxation; time-varying curve
收稿日期:20220630
網络出版日期:20220914
基金项目:兵团财政科技计划项目(2021BB022)
作者简介:夏腾腾(1998—),男,甘肃天水人,硕士研究生,主要从事材料性能研究与应用方面的研究。
通信作者:葛陈勇,E-mail:329439500@qq.com

