基于多阶段聚类的PM2.5质量浓度预测及对比研究

金宇凯，李志生，欧耀春，张华刚，曾江毅，陈搏超

（广东工业大学 土木与交通工程学院，广东 广州 510006）

近年来，随着我国经济和工业的发展，空气污染逐渐成为了一个不容忽视的问题。PM2.5是最主要的空气污染物，其直径≤2.5 μm，是一种能够悬浮于大气中的细颗粒物。在许多流行病学研究中PM2.5都与对公众健康的不利影响有关[1-2]。研究报告还认为，PM2.5暴露是影响心血管发病率和死亡率的因素[3-4]。随着我国对于环境的进一步治理，PM2.5以及其他空气污染物体积分数的增长有所放缓，但由于局部气象条件的改变，仍会使空气污染加剧[5]。因此，准确预测PM2.5变得尤为重要。

近年来，随着机器学习尤其是深度学习的发展，许多学者开始使用深度学习技术进行预测，例如白盛楠[6]、赵文芳[7]等使用长短期记忆网络(Long Short Term Memory，LSTM)方法进行PM2.5质量浓度预测，此外，还发现门控循环单元 (Gate Recurrent Unit，GRU)在计算时间和性能方面优于 LSTM。并且在不同的地区表现出不同的情况，如与时间和空间有关的不同情况[8-10]，因此空气质量预测可能有不同的结果。因此，单个预测模型可能不足以在不同情况下进行预测。

考虑到上述方法的局限性，混合模型已广泛应用于空气污染预测。混合模型可以整合每个算法的优势，以实现更好的模型性能。许多相关研究表明，混合模型往往具有更好的预测性能[11-15]，能在PM2.5质量浓度预测中广泛应用。

随着混合聚类算法的兴起，改良的混合模型在数据挖掘与分析领域得到了广泛应用[16-17]。Huang[18]等开发了一种深度Kmeans算法，Alguliyev[19]等将Kmeans算法应用于大数据，李如梅[20]等使用Kmeans分析夏季VOC的来源，周军锋[21]等构建BIRCH模型并应用于搜索领域，乔少杰[22]等利用高斯混合模型进行轨迹预测，崔玮[23]等基于高斯混合模型开发定位算法，宋董飞[24]等构建并优化了DBSCAN算法。

不过，已有研究仍然存在不足之处，神经网络等深度学习技术预测精度高，但容易陷入局部极小化[25]且收敛速度慢。Kmeans算法具有原理简单、计算速度快、集群效果优异等优点[26]，高斯混合模型是Kmeans算法的优化，HDBSCAN[27]和Agglomerative[28]等聚类算法也得到了较为广泛的应用，然而利用这些聚类算法多阶段叠加，并与深度神经网络[29-31]预测相结合，目前国内尚未有人研究。

本研究基于多阶段聚类结合PM2.5质量浓度预测构建混合模型，探讨多个模型的差异，通过对比各模型的预测结果，建立适用 PM2.5质量浓度预测的多阶段预测模型。

1 方法

1.1 HDBSCAN聚类

HDBSCAN (Hierarchical Density-based Spatial Clustering of Applications with Noise, 简称HDB)是一种分层密度聚类算法，这种算法扩展了DBSCAN，并将其转化为一个层次聚类算法，然后利用一种基于聚类稳定性的技术提取平面聚类。HDBSCAN相比于DBSCAN的最大优势在于不用人工选择领域半径和MinPts，只需选择最小生成类簇的大小，算法可以自动地推荐最优的簇类结果。同时定义了一种新的距离衡量方式，相互可达密度(mutual reachability distance)，可以更好地反映点之间的密度：

式中：corek(a)、corek(b)分别为第a、b个点到第k个点的距离。

HDBSCAN首先计算数据集中所有数据点关于参数m的核心距离。其中，核心距离定义为某个数据点到第m个点的近邻欧氏距离：

式中：D为点(xi,yi)与点(xj,yj)之间的欧氏距离。

接下来通过Prim算法构建最小生成树。Prim算法是图论中的一种算法，最早由捷克数学家沃伊捷赫·亚尔尼克[27]提出，该算法可在加权连通图里搜索最小生成树，构建连通图的集群层次结构。按权重递增顺序对最小生成树的边进行排序、迭代，为每个边创建一个新的合并集群，压缩集群层次结构。对于树的根，为所有对象分配相同的标签，并按权重递减顺序从层次结构中迭代删除所有边。每次删除后，将标签分配给包含已删除边的末端顶点的簇，得到最终聚类标签，若簇中的数据个数小于m，那该簇将会标记为离群点。

1.2 Kmeans聚类

Kmeans通常被称为劳埃德算法。Kmeans的算法步骤为：

(1) 选择初始化的K个样本作为初始聚类中心；

(2) 针对数据集中每个样本xi计算它到K个聚类中心的距离并将其分到距离最小的聚类中心所对应的类中，使用欧氏距离公式（式(2)）计算距离；

(3) 针对每个类别aj，重新计算它的聚类中心(即属于该类所有样本的质心)；

重复上面(2)、(3)两步操作，直到达到某个中止条件(迭代次数、最小误差变化等)。

1.3 Agglomerative聚类

凝聚层次聚类(Agglomerative Hierarchical Clustering, AHC)可在不同层次上对数据集进行划分[28]，形成树状的聚类结构，其原理是：最初将每个对象看成一个簇，接下来将这些簇通过算法一步步合并，直到达到预设的簇类个数。Agglomerative聚类使用欧氏距离计算不同类别数据点间的距离(相似度)。

1.4 高斯混合聚类

高斯混合模型(Gaussian Mixture Model, GMM)，是一种流行的聚类算法，该方法使用了高斯分布作为参数模型[22]，并使用了期望最大(Expectation Maximization, EM)算法进行训练。

其概率分布为

式中：K为聚类的个数；ak为第k个高斯的概率；p为第k个高斯的概率密度，其均值向量为μk；Σk为协方差矩阵。

1.5 BIRCH聚类

综合层次聚类算法 (Balanced Iterative Reducing and Clustering Using Hierarchies, BIRCH)适合于数据量大的数据集，运行速度快，只需单遍扫描数据集就能进行聚类[21]。

BIRCH算法的原理为利用一个树结构来帮助实现快速的聚类。结构类似于平衡B+树，一般将它称为聚类特征树(Clustering Feature Tree)。树的每一个节点由若干个聚类特征(Clustering Feature，CF)组成。每个节点包括叶子节点都有若干个CF，而内部节点的CF有指向叶子节点的指针，所有的叶子节点用一个双向链表链接起来。CF可以用PCF三元组来表示

式中：Ncluster为该聚类簇下点的数量；S为簇内各点之间的线性向量之和；R为簇内各向量的平方和。

1.6 DNN

深度神经网络(Deep Neural Network，DNN)是深度学习的一种框架[30]，它是一种具备至少一个隐含层的神经网络。DNN结构如图1所示。与浅层神经网络类似，深度神经网络也能够为复杂非线性系统提供建模，但多出的层次为模型提供了更高的抽象层次，因而提高了模型的能力[29]。DNN的激活函数在本文选择ReLU，ReLU的有效性体现在2个方面：克服梯度消失的问题，加快训练速度[31]。

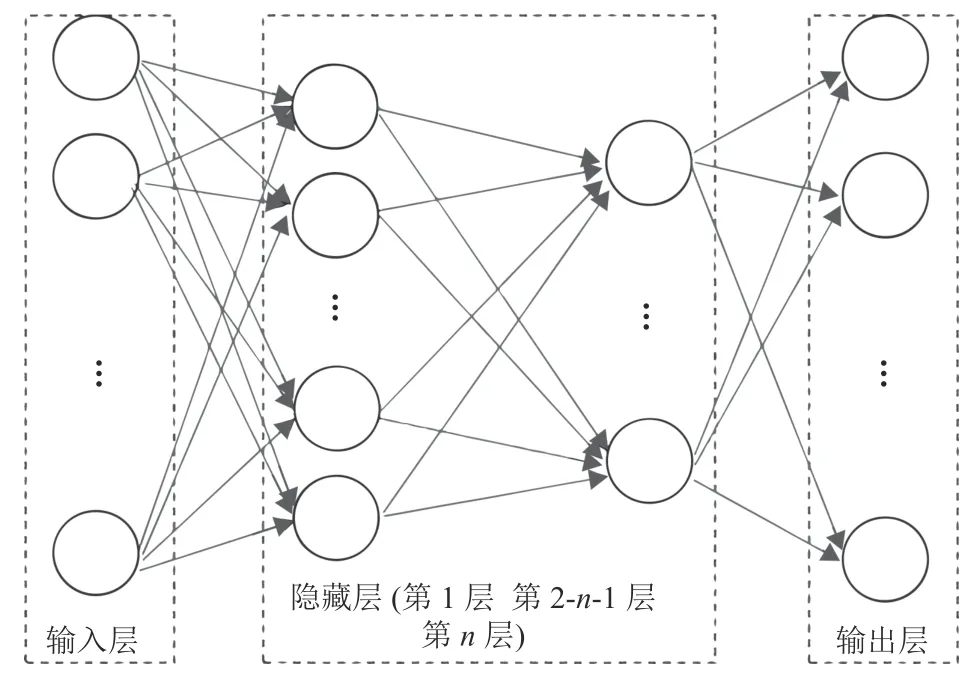
图1 深度神经网络结构Fig.1 Deep neural network structure

式中：x为输入值。

2 案例研究

2.1 研究区

深圳是我国的一线城市，也是粤港澳大湾区的中心城市之一。同时深圳是中国车流量最大的口岸城市，经济和工业发展速度快，是中国现代化城市的代表。本文选取了荔园、洪湖、华侨城、南油、盐田、龙岗、西乡、南澳、葵涌、梅沙、观澜共计11个空气质量监测站(如图2所示)，为了更好地分析深圳市的PM2.5质量浓度，本文计算所有监测站的平均值作为整个城市的空气质量特征[32]。

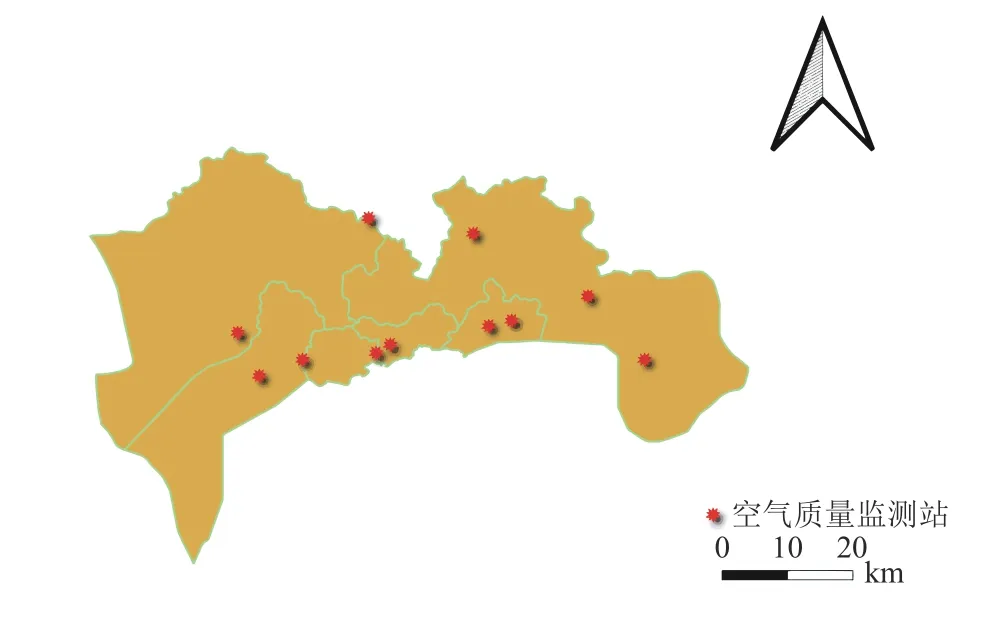
图2 深圳市空气质量监测站分布Fig.2 Distribution of air quality monitoring stations in Shenzhen

2.2 数据源

本研究采用的数据主要包括深圳市2015年全年的空气质量监测历史数据、气象监测站历史数据。其中，空气质量监测数据来自中国环境监测总站的全国城市空气质量实时发布平台(http://106.37.208.233:20035/)的逐时数据，气象监测站历史数据来自全国温室数据系统(http://data.sheshiyuanyi.com/WeatherData/)。

2.3 数据预处理

首先进行数据划分，使用sklearn的train_test_split函数对数据集进行随机划分，消除偶然性，取训练集7 008条(80%)，测试集1 752条(20%)。

其次，由于实际监测数据存在异常离群值或缺失值等情况，需要对初始数据进行筛选和填补。通过对样本进行四分位法分析，得出数据中共有552条缺失值，约占据了总数据(8 760)的6.3%，直接删除可能会产生精度影响，因此选择线性插值[33]对数据进行插补。相比于传统的均值填补降低数据方差的方法，本方法对于相邻时间段内缺失的数据，使用前后两个时刻的数据进行线性插值，能够有效地减小误差：

式中：t为缺失值的时间节点；u和v分别为t时刻前和t时刻后未缺失数据的时间节点；yu，yv为u，v时刻的监测值；L(t)为计算结果，即插补值。

从图3中可以看出，PM2.5反映出周期性与相似性。因此，在模型的设计中加入了时间特性，能更好地预测数值趋势。

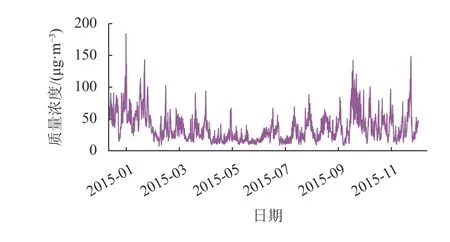
图3 2015全年深圳市PM2.5逐时质量浓度Fig.3 Hourly concentration of PM2.5 in Shenzhen in 2015

2.4 相关性分析

相关性分析采用皮尔森相关系数：

式中：rxy为变量x和y的Pearson相关系数，n为观测对象的数量，xi为x的第i个观测值，yi为y的第i个观测值。

从图4可以看出，PM2.5与5个空气污染物体积分数以及气压和日照时数呈现正相关，与风速、气温和湿度为负相关。其中，与NO2和CO较为相关，相关系数分别达到了0.69，0.68。应当指出，如果自变量和因变量之间的相关性过强(>0.8)[32]，则两者之间没有区别。如果自变量和因变量之间的相关性太弱(<0.55)[34]，则它们之间没有相关性。这两种情况下聚类是没有效果的[32]。因此，为了确保输入样本的多样性，需要综合考虑自变量和因变量之间的相关性和独立性。NO2与PM2.5的相关系数的绝对值符合要求，因此本文选择NO2与PM2.5进行聚类。

2.5 实验流程

本次实验的环境搭建使用的是Python3.7.6，Tensorflow2.2.0。

PM2.5质量浓度预测共分为数据预处理、模型建立以及预测输出3个部分，如，如图5所示。

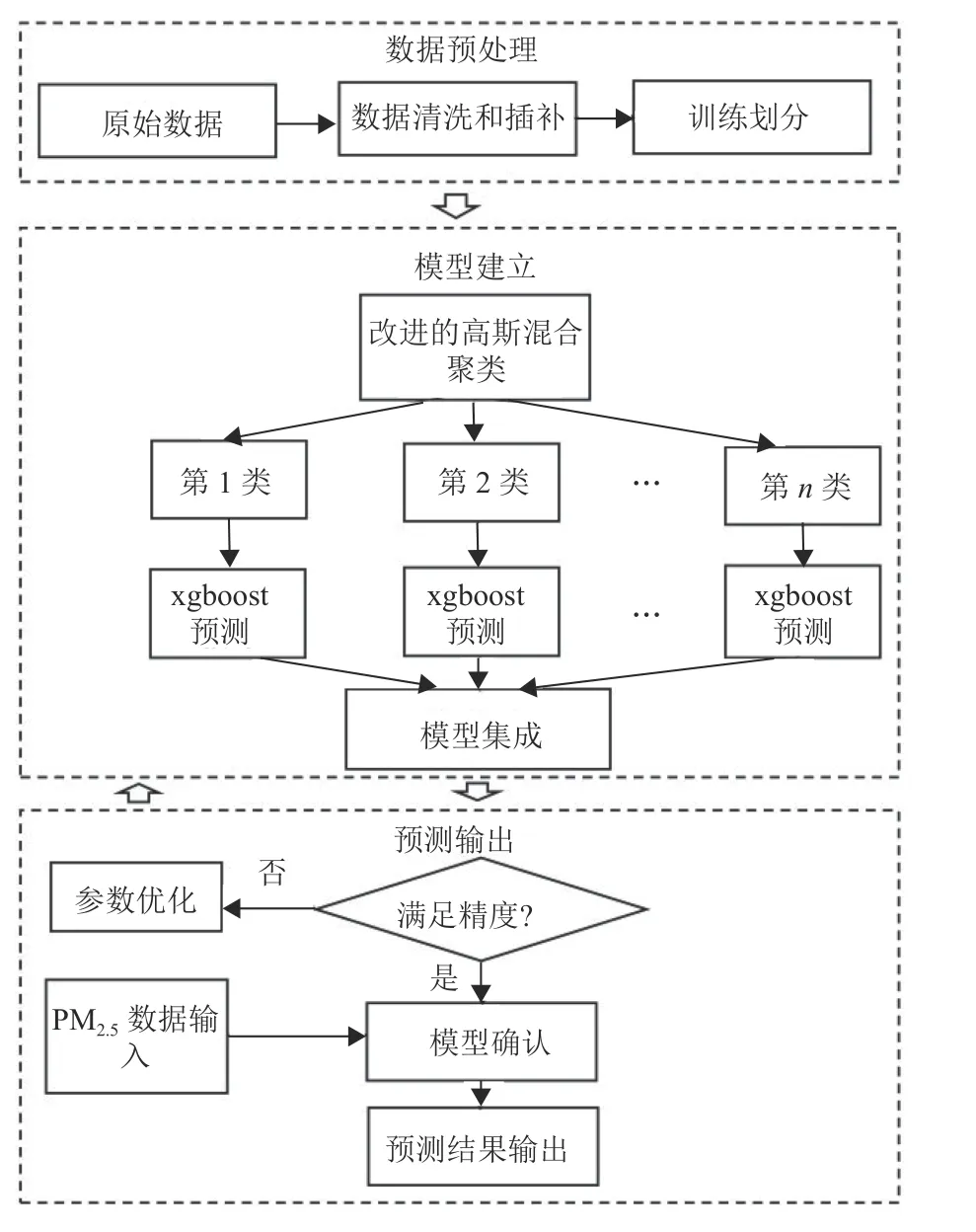
图5 实验路线图Fig.5 Experimental Roadmap

2.5.1 数据预处理

数据预处理如上文所述。自变量共包含风速、气温、日照时数、气压、湿度、PM10质量浓度(wPM10)、O3体积分数( φO3)、NO2体积分数(φNO2)、CO体积分数(φCO)、SO2体积分数(φSO2)共10个变量。

2.5.2 模型建立

(1) 第1阶段聚类。第1阶段使用密度聚类识别离群值。与传统离群值监测方法相比，密度聚类更加准确[35]，能够有效减少误删。并且，由于Kmeans、BIRCH等算法对噪点较为敏感，第1阶段聚类需要识别出噪点并进行剔除(剔除后使用线性插值进行插补)。HDBSCAN较为符合这个特点。

(2) 第2阶段聚类。Kmeans、高斯、AHC聚类算法需确定一个超参数，即簇数，使用轮廓系数法确定。BIRCH需要选择簇数以及权重系数2个参数，首先采用网格搜索进行权重系数的选择，然后采用轮廓系数法进行簇数选择

(3) DNN预测。首先根据DNN的特性，进行算法初始参数设置。再根据输出结果的情况，进行调节参数以及参数选取设置。然后利用训练集进行模型训练，保存最优模型。经过调参，最优模型的隐藏层为4层，节点数分别为128，64，32，32。激活函数选择ReLu，学习率设置为0.1。

2.5.3 预测输出

建立好模型并且精度达到要求后，将预测数据输入模型，最后得到预测结果。

2.6 模型评价

为了合理评价模型的综合性能，本文分别构建平均绝对误差MAE、均方差RMSE、平均绝对百分比误差 MAPE 、相关系数R这4个指标对模型进行评估。MAE能更好地反映观测值误差的实际情况，RMSE 用来衡量观测值和真实值之间的偏差，两者的研究目的不同。4个指标的定义公式为

式中：n为数据的数量；cti为第i个样本点污染物质量浓度真实值(μg/m3)；cpi为第i个样本点污染物质量浓度预测值(μg/m3)；cp和ct分别为预测结果和真实结果的平均值(μg/m3)。

3 结果分析

3.1 第1阶段聚类

3.1.1 轮廓系数法

聚类前，首先对数据进行归一化处理。在本模型中，使用HDBSCAN作为第1阶段聚类算法，HDBSCAN只需调节1个超参数，即最小聚类规模(min_cluster_size)，通过调节该参数可以自动计算簇数。本文采用轮廓系数法(Silhouette Coefficient, 以下简称S)确定超参数，S越大，表明聚类效果愈好[36]。

式中：di为第i个簇，N为点的个数。

3.1.2 聚类结果

如图6(a)所示，轮廓系数最大值为最小聚类规模等于9的时候，轮廓系数为0.432。图6(b)为聚类后的结果，可以看出，大部分的离群值被识别出，并使用了灰色进行标识。此外，还有两团微小簇，个数分别为9和10，考虑到这两簇的位置更接近离群值，因此也将这两簇归为噪声，共得到329条(3.7%)噪声值，采用线性插值进行插补。

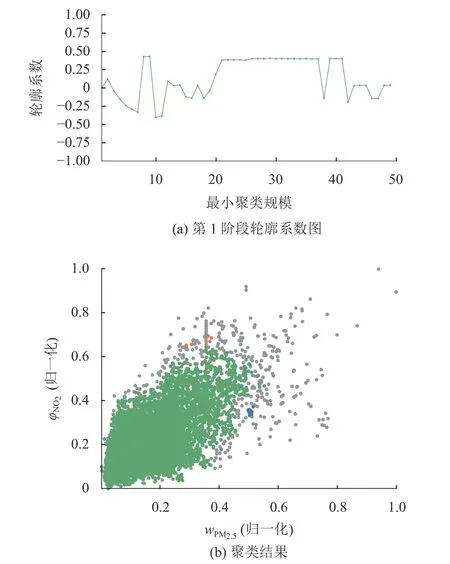
图6 HDBSCAN轮廓系数图和聚类结果图Fig.6 Contour coefficient graph and clustering result graph of HDBSCAN

3.2 第2阶段聚类

确定簇数。如图7所示，4种聚类算法均在K=2，即在2簇时达到了轮廓系数最大值，高斯混合聚类轮廓系数较低，为0.45，AHC、BIRCH、Kmeans聚类较为接近，分别为0.54，0.56，0.54。图8显示了4种聚类的结果。

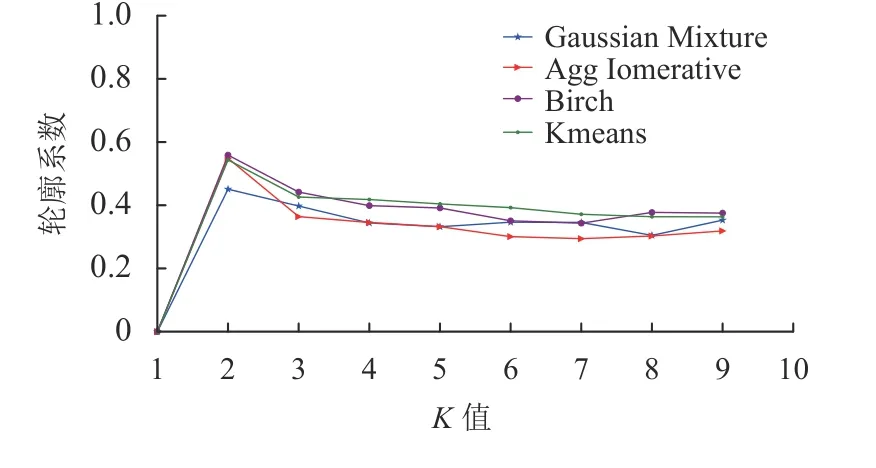
图7 第2阶段聚类轮廓系数图Fig.7 Second stage clustering contour coefficient graph

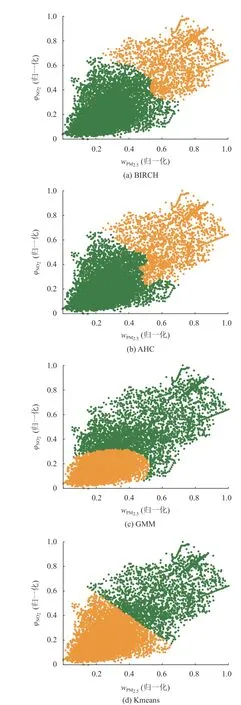
图8 4种模型第2阶段聚类结果Fig.8 The second stage clustering results of four models

3.3 DNN预测

精度分析。为了分析多阶段聚类的性能，本文选择了单阶段聚类以及不进行聚类的6个预测模型作为对照。所有模型都以原始数据计算精度。预测结果如图9所示。

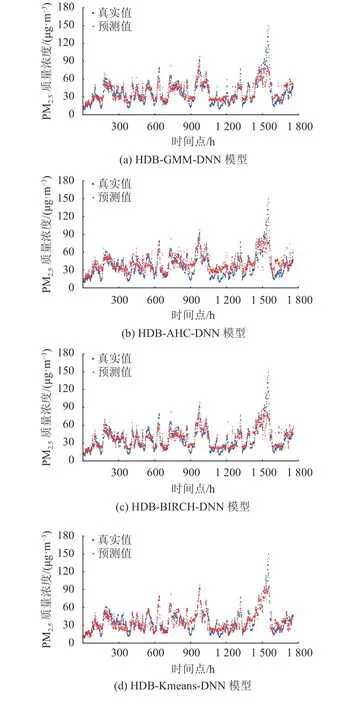
图9 4种模型预测值与真实值的对比Fig.9 Comparison of predicted value and real value of four models

通过分析，一阶段和多阶段聚类的预测模型较DNN模型均获得了不同幅度的提升(见表1)。在单阶段聚类模型中，BIRCH-DNN模型是最优模型，4个指标均获得了20%左右的提升。在多阶段聚类模型中，HDB-Kmeans-DNN模型提升最大，4个指标较单步预测模型分别提升了3.39，3.23，2.36，0.08，约提升了20%。HDB-AHC-DNN模型提升较不明显，HDBGMM-DNN模型和HDB-BIRCH-DNN模型预测能力较为接近，但后者的时间消耗更短。

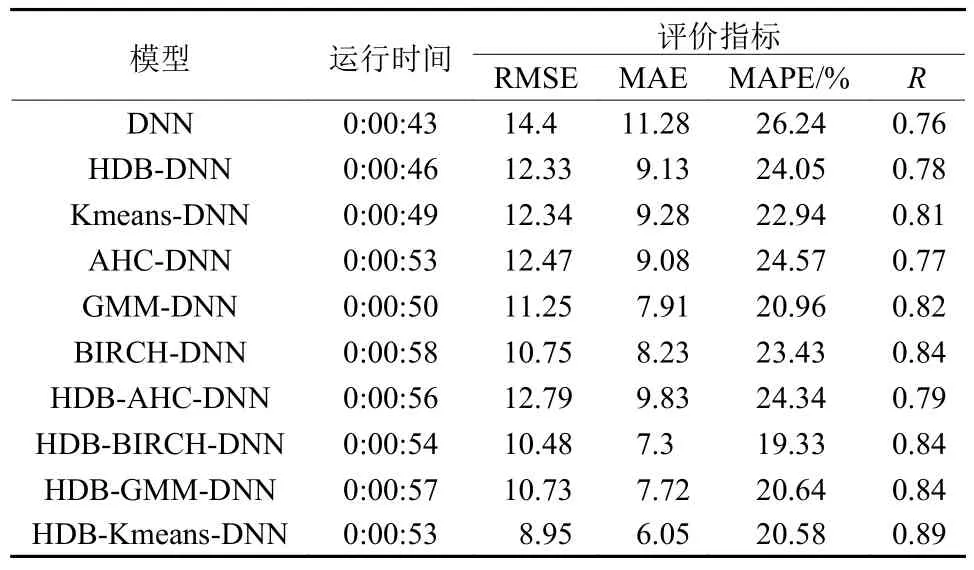
表1 不同模型预测结果Table 1 Predict results of different models

4 结论

本研究建立了基于多阶段聚类的PM2.5预测模型，以预测和分析PM2.5的小时平均质量浓度。并用多阶段聚类预测模型与其他的非聚类预测模型以及单阶段聚类预测模型进行比较，以证明其有效性。相关性分析结果表明，NO2和CO的体积分数在预测PM2.5质量浓度方面发挥重要作用，其中NO2与PM2.5更为相关，相关系数为0.69。

聚类结果显示，PM2.5聚类处理后，噪声基本消除，PM2.5的周期性变得更加稳定。

本研究的不足之处在于，PM2.5极高质量浓度值的预测不太理想，今后可能需要优化聚类算法以及预测算法，以提升极端空气污染的预警能力。

本研究的结论如下。

(1) 提出了基于多阶段聚类的PM2.5预测模型，较传统深度学习模型大幅度提升了精度，预测效果较好。

(2) 提出了一种基于HDBSCAN聚类的去除噪点方法，实验结果表明，这种方法适用于多阶段聚类预测模型。

(3) 对比了多种常规聚类算法，实验结果表明，不同的算法在聚类效果和预测效果上具有显著差异，其中HDB-Kmeans-DNN模型精度和误差较为理想，可以应用于实际预测。