玻璃文物化学成分的相关性关系探究

贾宇航

（西安交通大学，陕西西安 710049）

0.引言

对考古发掘的玻璃制品的化学成分分析是研究历史的重要手段。针对不同风化程度的出土玻璃制品，研究其内部化学元素风化前后的变化规律，探究各种化学成分的内在联系，有利于对风化文物先前的化学成分进行预测还原，品类鉴定，对考古工作意义重大[1]。

本文的研究是基于2022 年中国大学生数学建模竞赛的C 题（部分），为探究玻璃内化学成分的关联关系给出了一种简便而有效的方法。在原题目中，给出了高钾，铅钡两种类型玻璃的各种化学成分含量的样本，且二者分别有属于风化前、风化后的采样点，本文基于传统统计学的一系列方法对该问题进行了有效的分析，也对考古界实际应用提供了思路。

1.化学成分间的相关性分析

考察变量间的相关关系，应使用相关性分析。主要考虑的是Pearson 相关性分析和Spearman 相关性分析，其中，前者使用条件是数据满足正态分布，否则，应采用后者。

对于不服从正态分布的数据，在相关性分析时应选取Spearman 相关性分析。基于此，对四组（高钾风化，高钾无风化，铅钡风化，铅钡无风化）的各个化学成分分别单独做两两的相关性分析，并将相关性分析结果可视化做出热力图，如图1 所示。

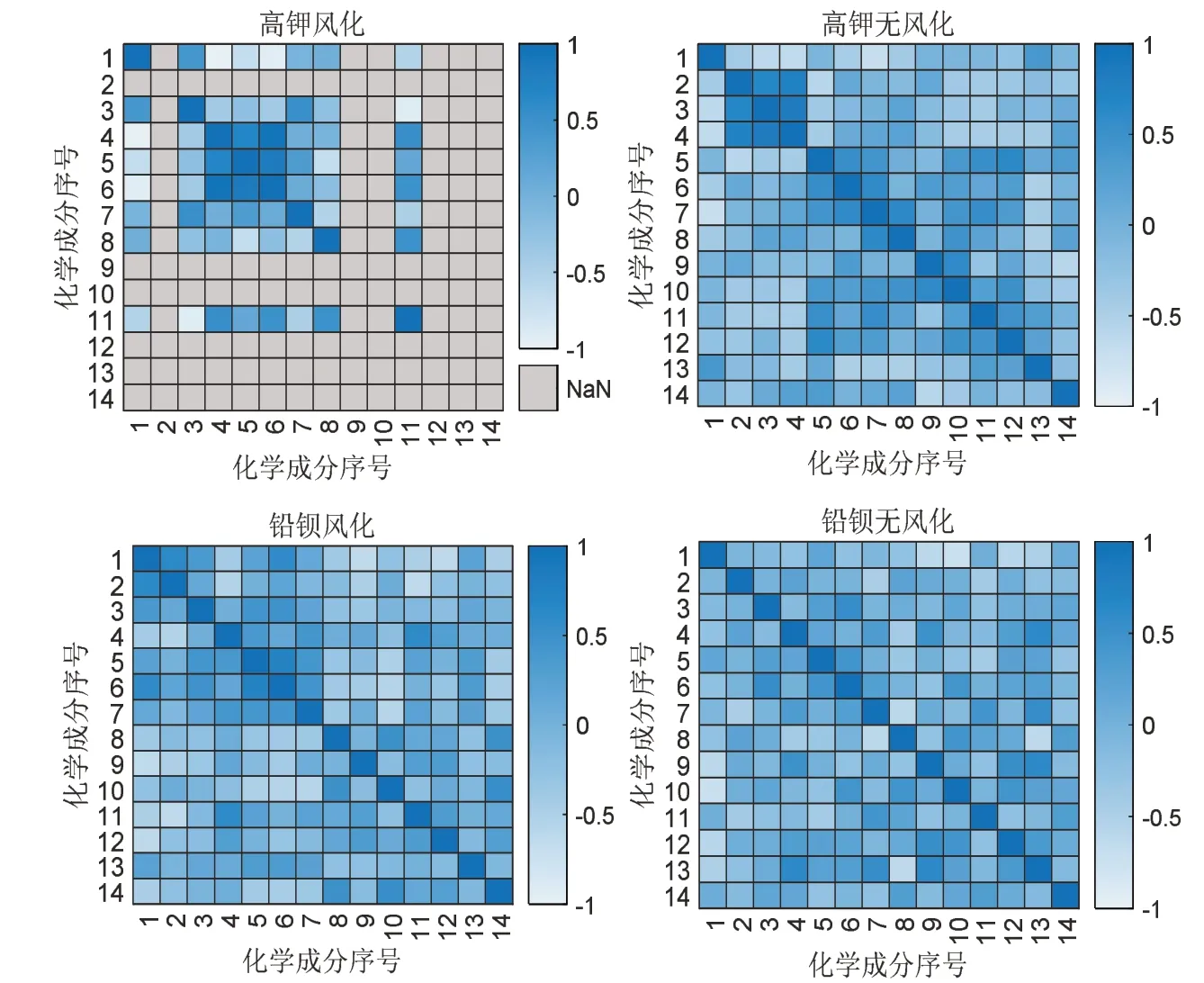
图1 组各自的相关性分析热力图

以“铅钡风化”为例，把二氧化硅（SiO2），氧化钠（Na2O），氧化钾（K2O），氧化钙（CaO），氧化镁（MgO），氧化铝（Al2O3），氧化铁（Fe2O3），氧化铜（CuO），氧化铅（PbO），氧化钡（BaO），五氧化二磷（P2O5），氧化锶（SrO），氧化锡（SnO2），二氧化硫（SO2）这14 种化学成分，做出各成分含量的分布图，仅有SiO2，PbO，SrO的含量服从正态分布，其他则非然，故选取Spearman相关性分析。

在“高钾风化”组中，由于存在众多全部为0 值的化学成分，无意义，以NaN 表示。其余各个成分的两两相关性分析显示出-1 ～1 的计算值，分别用白色和蓝色表示，中间为过渡色带。相关系数的大小将相关程度分为以下几种情况。

2.基于岭回归的多成分相互作用关系探究

相关性分析只是说明了两两化学成分的相关关系，但难以考虑到多种化学成分互相影响的机制。事实上，众多化学成分应该是互相作用的，由此想到通过回归分析的方法来对多种化学成分进行定量的拟合[2]。存在不少两两相关系数很强成分组，这将导致多重共线性的产生（VIF>10），因此，传统多元线性回归方法失效，故本文采用岭回归的方法分析。

岭回归（Ridge Regression）实际上是对多元线性回归的改进。岭回归主要解决的问题是数据集之间具有多重共线性，即预测变量之间具有相关性[3]。

在一般情况下，使用最小二乘法求解上述回归问题的目标是最小化，岭回归就是要在上述最小化目标中加上一个惩罚项，如下式描述：

这里的λ 也是待求参数。也就是说，岭回归是带二范数惩罚的最小二乘法回归。

以“高钾风化组”为例，选出相关系数>0.5 的组合，作为目标化学成分，然后，挑选出出现次数较多的成分序号作为因变量，认为这些成分可能与其他众多成分存在多元回归关系，最终选出5（MgO）和11（P2O5），与之对应自变量的成分序号分别为：1（SiO2），4（CaO），6（Al2O3），8（CuO）和1（SiO2），3（K2O），4（CaO）。

按此方法，对其余的各项大类中的各个存在较强相关性的化学成分变量做多元岭回归。把R作为考量回归效果的重要指标，从而剔除所有R小于0.5 的回归方程，其余则视为合理。最终，得到如下4 个大类下的各化学成分相关关系。一共有五条符合要求的回归方程，如表1 所示。

表1 4种类别下的回归方程

从中可以看出每组内的化学成分的关系式。此外，我们还可以比较不同组之间的异同，总体来看：（1）不同类型和是否风化造成了相关的化学成分的不同，如铁、铜的相关性在高钾无风化组中体现；P2O5只在高钾无风化组中参与成分间关系式的构建。（2）不论高钾/铅钡，风化后，成分之间相关的多元性变差了。

3.回归模型的合理性检验

如图2 中给出了岭回归结果检验，通过比较真实值与回归值的差异，目的是验证回归效果的良好性。在5 幅图中，由上至下分别对应回归方程1 ～5。

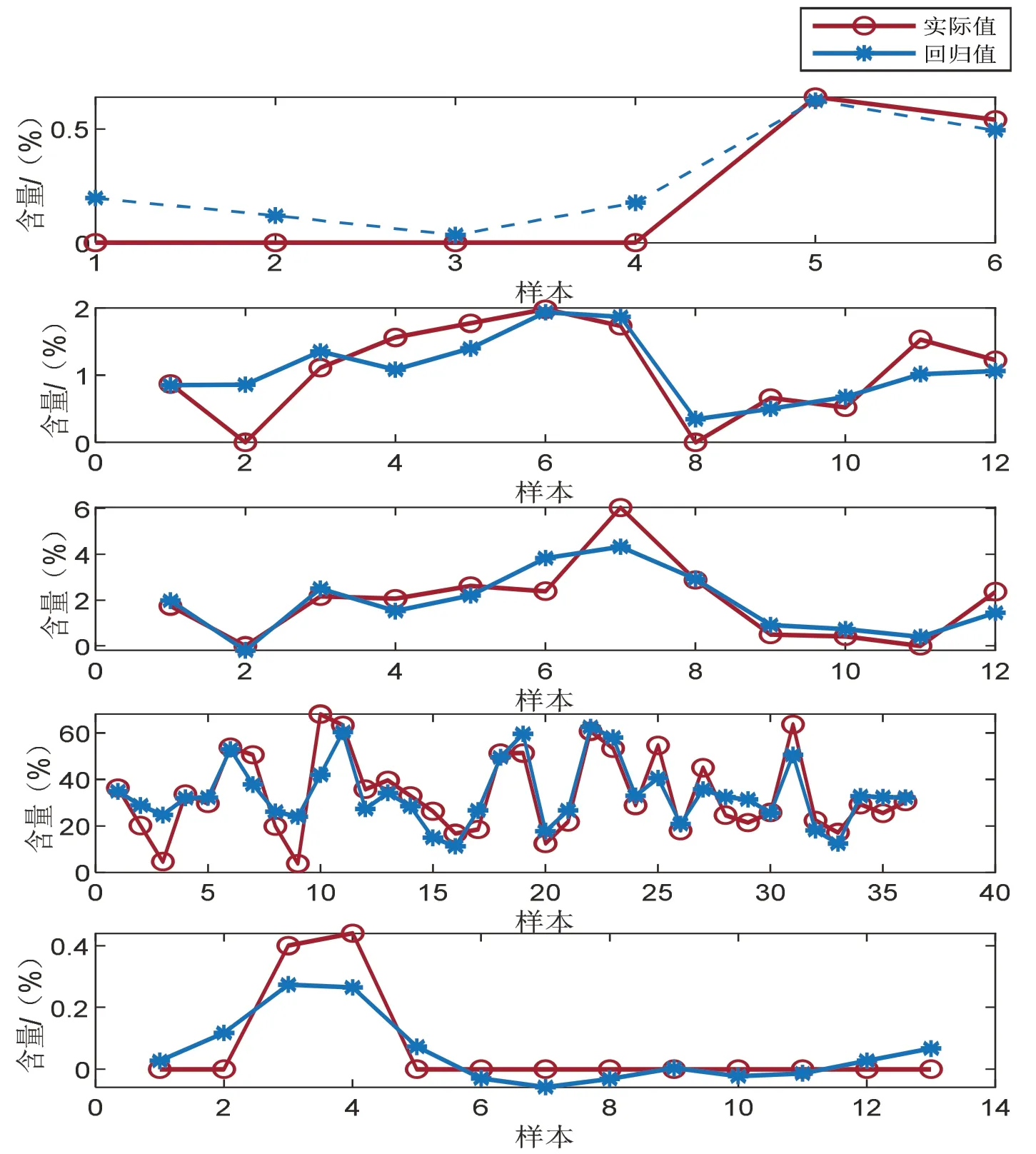
图2 真实值与回归值比较

可以看出，模型整体回归效果良好，真实值与预测值的偏差很小。说明岭回归模型是合理的。对于样本数较多的组来说，如第四条回归方程，可以看出拟合效果非常好，实际值与回归值几乎完全一致。而对于数据样本较少的组来说，效果略微逊色，但整体上，该五条回归方程的调整R都达到0.8 及以上，认为岭回归是有效的，也就是说基于抽取玻璃文物化学成分的相关性关系分析进行玻璃文物考古有效可行[4]。

4.结论与分析

就相关性而言，发现高钾玻璃风化前中共有11 组成分，具有较强的关联性，而风化后有12 组化学成分两两具有较强相关性，差别不大；对铅钡玻璃来说，风化前有15 组化学成分两两呈现较强相关性，但风化后仅有11组，略有下降，由此间接印证了铅钡玻璃比高钾玻璃更容易受到风化的影响。

不论高钾还是铅钡玻璃，参与回归方程变量构建的个数在风化后都有所下降，高钾玻璃风化前有7 种化学成分参与了多元回归，风化后只有5 种；铅钡玻璃则是由6 种变为风化后的5 种。风化导致了玻璃内化学成分多重的相互作用关系变弱了，或可能是由于某些化学成分在风化中急剧减少或增加，从而失去了同其他化学成分原有的相关关系。从某种意义上说，在玻璃文物领域中，有大量的文物数据没有被充分研究并利用。对于某一新出土的玻璃文物而言，本文更加具有现实意义。