一种数据驱动的气动热预示模型

王 泽，王梓伊，王 旭，宋述芳，张伟伟，*

(1. 西北工业大学 航空学院，西安 710072；2. 中国空气动力研究与发展中心，绵阳 621000)

0 引 言

高超声速飞行器是现今各国研究的热点，无论是飞行器的热防护设计还是热气动弹性分析，气动热的高效精准预示都是极为关键的问题[1-2]。传统的气动热预示手段主要包括飞行试验、地面风洞试验、工程算法和数值模拟等方法。飞行试验和地面风洞试验虽然可以准确预示飞行器的气动热，但是受成本限制，难以作为常规预示手段[3-4]。具有试验和理论基础的工程方法可以高效地进行气动热预示，但是因为其包含诸多假设，对复杂外形、流动的气动热预示精度低。数值模拟方法虽然可以实现对复杂外形飞行器较高精度的气动热预示，但是对网格质量要求高、收敛性差、计算量大，依旧无法满足工程设计中气动热的快速精准预示需求[5-6]。

为解决高超声速飞行器气动热高效精准预示问题，研究者们进行了大量探索。吕丽丽等[7]通过在边界层外求解Euler 方程获得无黏参数，边界层内使用工程算法预示热流，提高了工程算法对复杂外形的适用性。Mcnamara 等[8]通过两次数值求解获得物面绝热温度分布Taw和对流换热系数h，再利用Newton 冷却公式可以快速获得任意壁面温度Tw下的热流分布。Falkiewicz[9]通过本征正交分解（proper orthogonal decomposition, POD）对 F104 机翼表面瞬态温度场和热流场进行降阶，构建输入为来流参数和温度场模态系数、输出为气动热降阶分布的Kriging 代理模型，实现气动热的快速预示。陈鑫等[10-12]构建了输入为来流参数、输出为F104 机翼物面温度场POD 基系数的代理模型，并对该模型的构建方法和采样方法进行了深入研究。聂春生等[13]结合POD 方法和RBF 插值，建立了一种适宜复杂外形表面热流预示的代理模型，实现了沿给定弹道三维热环境快速预示。张智超等[14]提出了一种基于径向基神经网络的气动热快速预示代理模型方法，输入为来流参数，输出为每个网格节点热流预示结果。以上几种思路虽然都实现了气动热的快速精准预示，但是仍存在一些弊端：CFD 结合工程算法，虽然提升了对复杂外形的胜任性，但因工程模型的固有假设，精度仍有限；POD 降阶方法需要大量的训练样本，而且很难实现对几何外形的泛化；使用来流参数映射壁面热流，无法体现气动热的局部性特点。

近些年，机器学习技术得到了飞速发展，特别是可以依据有限样本信息实现最大泛化性能的支持向量机（support vector machine, SVM）已经被用于如偏微分方程求解[15]、图像识别[16]和气动力建模[17-19]等诸多领域。

本文提出了一种基于支持向量机和边界层理论的当地化气动热预示建模方法（boundary layer theory and support vector machine localized aeroheating modeling method, BSLM）。由边界层理论得知，壁面热流具有很强的当地性，是一个局部量，而且其分布很大程度上取决于边界层外缘信息[20]。基于边界层外缘信息和壁面热流间的密切关联，本文采用了数据驱动的当地化建模思路，利用SVM 构建了从当地边界层外缘特征到当地壁面热流的气动热预示模型。论文首先探究了边界层外缘特征对模型性能的影响，验证了特征选择方法的有效性；然后针对二级压缩面及双椭球开展气动热预示，分析了模型预示精度、泛化能力以及对非均匀分布壁面温度等当地化边界条件的适用性，并与传统POD 降阶模型方法进行了简要对比；最后，总结了研究结果，给出了相关结论。

1 气动热预示模型

1.1 支持向量机

SVM 是一种建立在VC 维（Vapnik-Chervonenkis dimension）理论和结构风险最小原理基础上的机器学习算法[21]。其核心思想是将回归问题经过严格数学推导转化为二次规划问题，并通过非线性映射将样本从原始空间映射到高维特征空间实现样本的线性可分。设样本训练集D={(x1,y1), (x2,y2), ···, (xm,ym)},xi∈Rn,yi∈R,i=1, 2, ···,m，xi为真实输入，yi为真实输出。考虑近似回归模型f(x)=ωTϕ(x)+b， ω和b是模型参数，ϕ(x)是样本x的非线性映射。给定真实输出y和模型输出f(x)的容忍偏差ϵ，支持向量回归问题可写为：

其中，C为正则化常数，ℓϵ为损失函数：

式（1）引入拉格朗日乘子αi≥0 、≥0，由拉格朗日乘子法得到式（1）的对偶问题：

对应KKT（Karush-Kuhn-Tucker）条件为：

其中ξi代表松弛变量，是支持向量机的优化参数。求解该对偶问题，得到拉格朗日乘子αi、及参数b，则近似回归模型f(x)可表示为：

1.2 特征选择

输入特征对机器学习模型性能的影响十分关键。特征不足难以全面展现数据的特性，不利于模型精度的提高；相反，特征冗余可能使模型过拟合，降低模型泛化性能[22]。为了挑选出有效特征，需要进行特征选择。常用的特征选择方法主要有经验选择法、逐一遍历法、过滤法、打包法和嵌入法等。本文使用过滤法和嵌入法结合的特征选择方法：首先对候选特征进行重要性排序，为避免某些包含关键信息的特征被丢弃，需将重要性低但包含关键信息的特征排序人为提前；然后从最重要的特征开始按顺序逐个地增加特征直到模型精度不再提高或遍历所有特征；最后选择模型预示性能最好的特征组合。其中，特征重要性排序使用随机森林（random forest, RF）。随机森林是一种并行式集成机器学习方法，内嵌平均不纯度减少算法用于计算特征的重要性。本文特征选择方法具体流程如图1 所示。

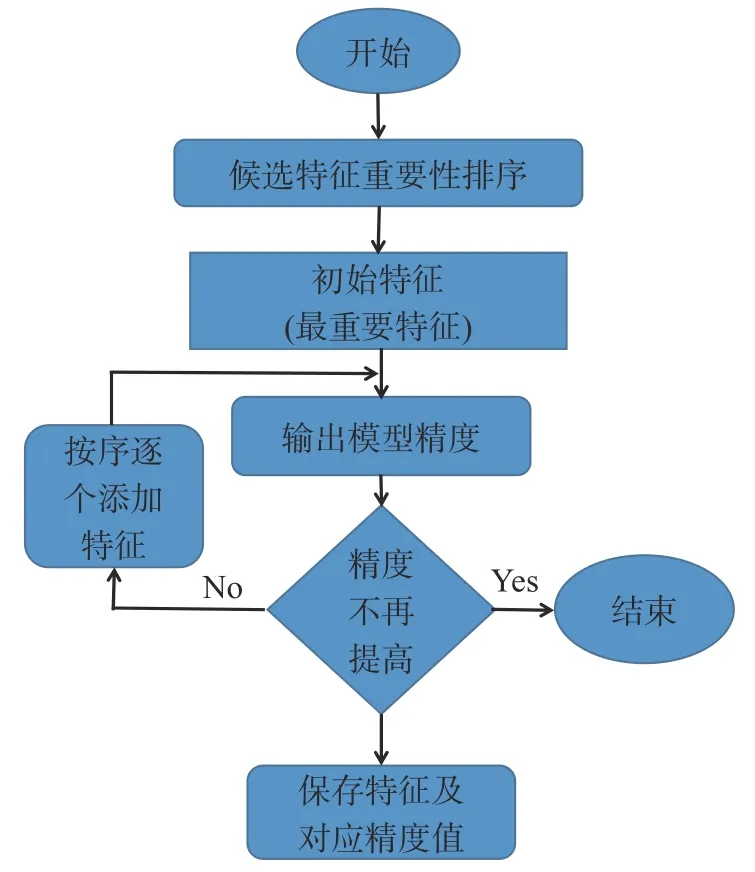
图1 特征选择流程图Fig. 1 Flow diagram of the feature selection

1.3 模型构建

气动热预示模型的构建过程如图2 所示。首先，求解Euler 方程获得边界层外缘信息。之后，根据边界层外缘信息构建出候选特征并进行特征选择，得到输入特征组合。最后，使用训练数据对支持向量机进行训练，并测试模型性能。至此，气动热预示模型构建完毕。

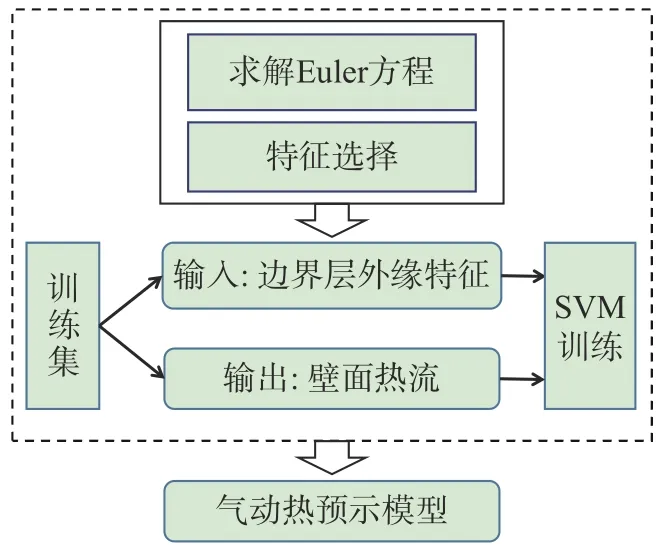
图2 气动热预示模型构建流程图Fig. 2 Flow diagram of the aeroheating prediction model construction

2 算例验证及结果分析

2.1 气动热数值计算方法验证

本文使用RANS 计算气动热样本数据，为保证数据精度需对RANS 计算方法进行验证。二维外形气动热计算采用AUSM+空间格式、 LU-SGS 伪时间推进和k−ωSST湍流模型，CFL 数取0.5，以高超声速圆柱作为验证算例[23]；三维外形采用Steger 空间格式、Minmod 限制器和k−ωSST湍流模型，CFL 数取0.5，以双椭球作为验证算例。

高超声速圆柱半径0.038 m，来流马赫数为6.5，雷诺数1.6×106/m，总温1 900 K，壁面温度294 K[24]。双椭球标模算例与文献[25]一致，来流马赫数为10.02，雷诺数2.2×106/m，总温1 457 K，壁面温度294 K，迎角−5°。二维圆柱和三维双椭球计算网格如图3 所示，第一层网格高度都为1×10−6m。图4 和图5 分别给出了圆柱和双椭球的壁面热流RANS 计算结果，两者都与试验结果高度吻合，本文采用的数值计算方法可以准确计算二维及三维外形的壁面热流。

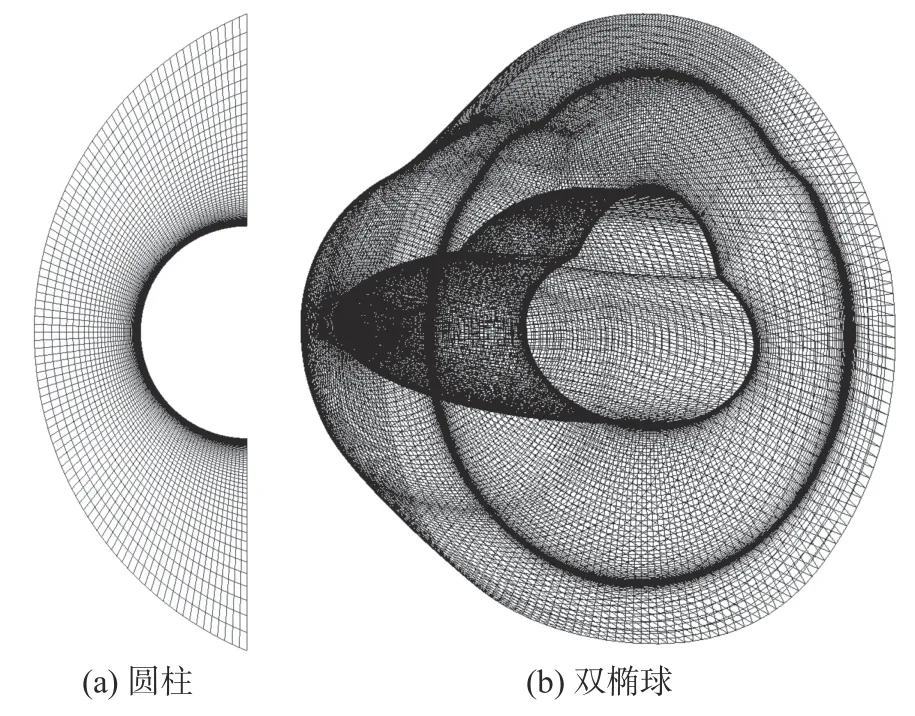
图3 高超声速圆柱和双椭球计算网格Fig. 3 Computational grids of the hypersonic cylinder and the double ellipsoid

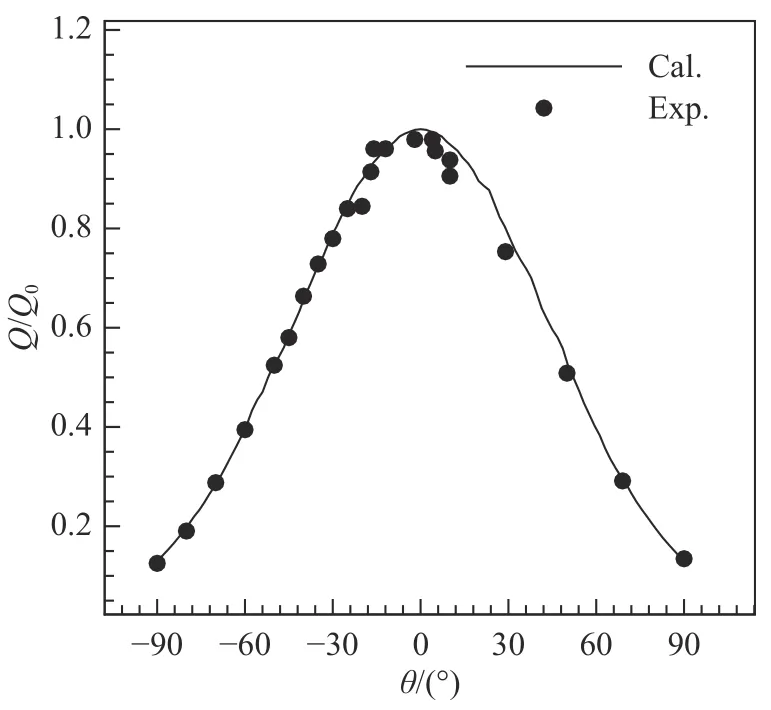
图4 圆柱壁面热流分布计算结果和试验结果对比Fig. 4 Heat flux distribution on the cylinder surface compared between the computational and experimental results

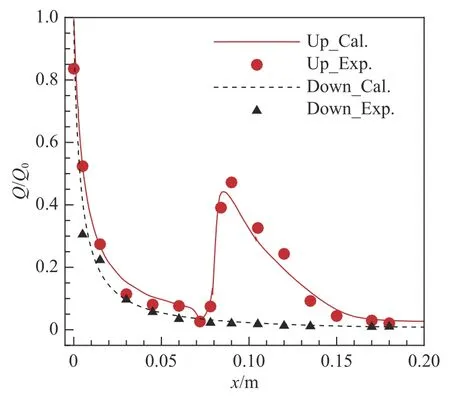
图5 双椭球表面中心线热流分布计算结果和试验结果对比Fig. 5 Heat flux distribution along the centerline of the double ellipsoid surface compared between the computational and experimental results

2.2 双椭球上表面中心线热流预示

本节利用双椭球上表面中心线热流预示算例对特征选择方法进行验证，对本文气动热建模方法（BSLM）进行初步测试，并与传统POD 降阶模型方法进行简单对比。

在每个迎角的双椭球上表面中心线抽取65 个点的边界层外缘信息和热流数据，取点位置及数量需保证表面热流的准确刻画。以迎角0°、10°、20°和25°的数据作为训练集，迎角15°的数据作为验证集，迎角5°和30°的数据作为测试集。根据边界层外缘信息和泛化对象构造候选特征，如表1 所示。s为流线长度，即双椭球上表面中心线任意一点沿壁面到前缘点的距离；αs=tan−1(ve/ue)为当地迎角；下标e 代表边界层外缘，下标 ∞代表来流，下标w 代表壁面。

表1 候选特征Table 1 Feature candidates

使用随机森林对候选特征进行重要性排序，结果如图6 所示。特征ρe/ρ∞和特征Pe/P∞的重要性大小远超其他特征，这两个特征作为首要选择。特征s和αs分别表示流线长度和当地迎角，虽然包含信息简单、特征重要性低，但是它们与其他特征组合后能刻画非常丰富的流场特性，是非常关键的特征。因此，根据经验将特征s和αs的排序提前到第3 位和第4 位，最终特征排序为f2＞f3＞f1＞f6＞f5＞f8＞f9＞f4＞f7。以f2 和f3 两个特征为初始特征组合，按顺序逐个增加特征，进行建模得到训练集和验证集的均方根误差（RMSE），结果如图7 所示。可以看出，随着特征的逐个增加，训练集和验证集的RMSE 值呈现先减小后增大的趋势，特征数量为5 的特征组合对应着最小的RMSE 值。因此，本算例选择特征组合[f2，f3，f1，f6，f5]进行热流预示。

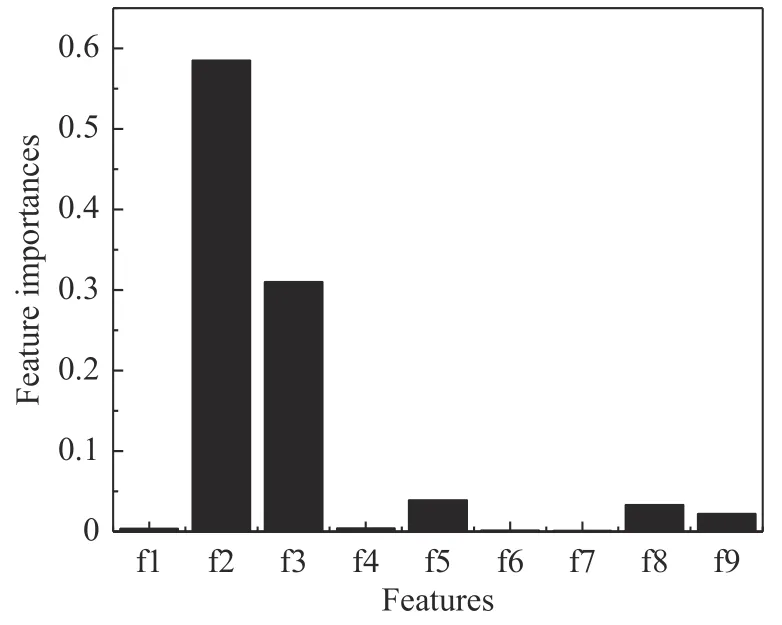
图6 特征重要性柱状图Fig. 6 Bar chart for the feature importance

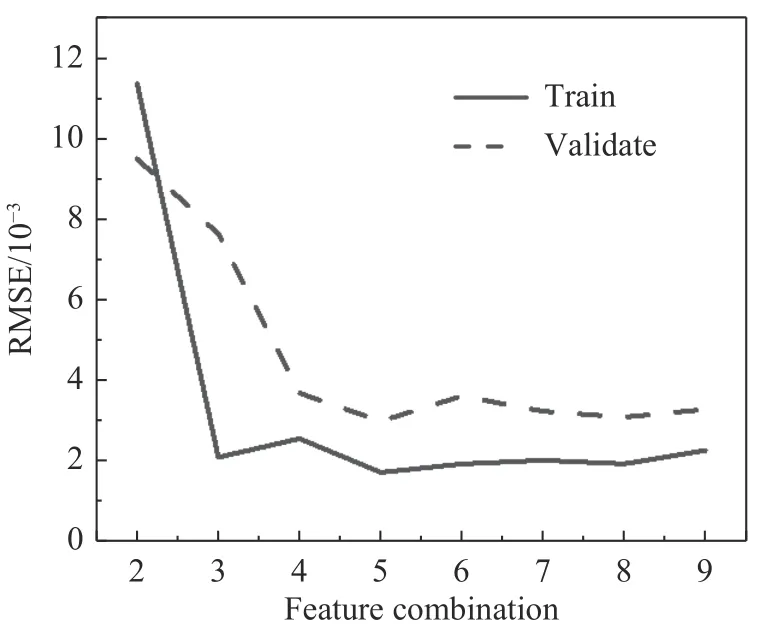
图7 不同特征组合下模型训练和验证精度Fig. 7 Model training and validation accuracy under different feature combinations

POD 方法使用的热流数据集与BSLM 方法相同，代理模型采用Kriging 模型。不同迎角双椭球上表面中心线BSLM 热流预示结果、POD 热流预示结果和RANS 结果对比如图8 所示，可以看出，BSLM方法预示的热流曲线与RANS 计算的热流曲线吻合很好，而且在前缘点处BSLM 方法预示结果明显好于POD 方法预示结果。如表2 所示，三组迎角下前缘点处BSLM 方法预示的热流值与RANS 计算值的相对误差（RE）都小于POD 方法；当α=30°时，BSLM方法的RE 值仅有POD 方法的8.71%。三组迎角下BSLM 方法预示的热流值与RANS 计算值的均方根误差（RMSE）也均小于POD 方法；当α=30°时，BSLM方法的RMSE 值仅为POD 方法的18.80%。BSLM 方法预示结果精度优于POD 方法的原因主要是：BSLM 方法是一种当地化建模方法，符合热流的当地性特点，而POD 方法构建的是全局模型；BSLM 方法不仅使用了热流信息，还使用了边界层外缘信息，相比于POD 方法信息更丰富。

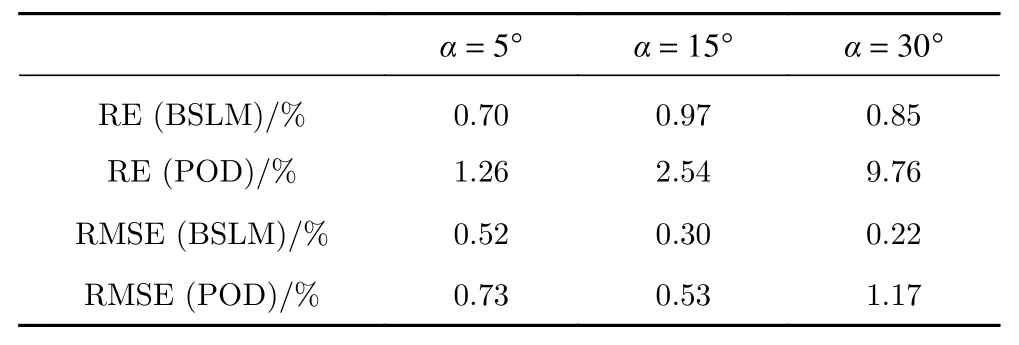
表2 BSLM 和POD 方法的RMSE 值和前缘点RE 值对比Table 2 RE at the leading-edge point and RMSE compared between BSLM and POD

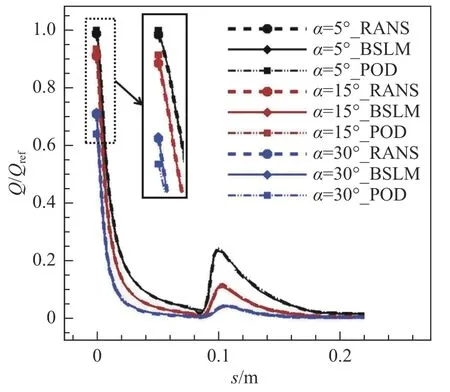
图8 BSLM、POD 热流预示值和RANS 计算值对比Fig. 8 Heat flux comparison between the calculation of RANS and the prediction of BSLM and POD

2.3 二级压缩面热流预示

在实际气动加热过程中，结构表面温度往往是非均匀分布的，因此，有必要进一步考察非均布壁面温度条件下BSLM 方法的适用性。

采用二级压缩面作为测试算例，该算例改动自某热气动弹性实验模型，其几何尺寸和计算网格如图9 所示，第一层网格高度1×10−3mm。来流参数选自30 km 高度的大气，以马赫数Ma和壁面温度Tw作为变量，数值计算格式与二维圆柱相同。训练状态和测试状态如表3 所示，标注“√”的状态为训练状态，标注“△”的状态为测试状态。此外，测试状态还包括Ma= 9、Tw非均匀分布的状态，Tw在二级压缩面的分布如图10 所示。

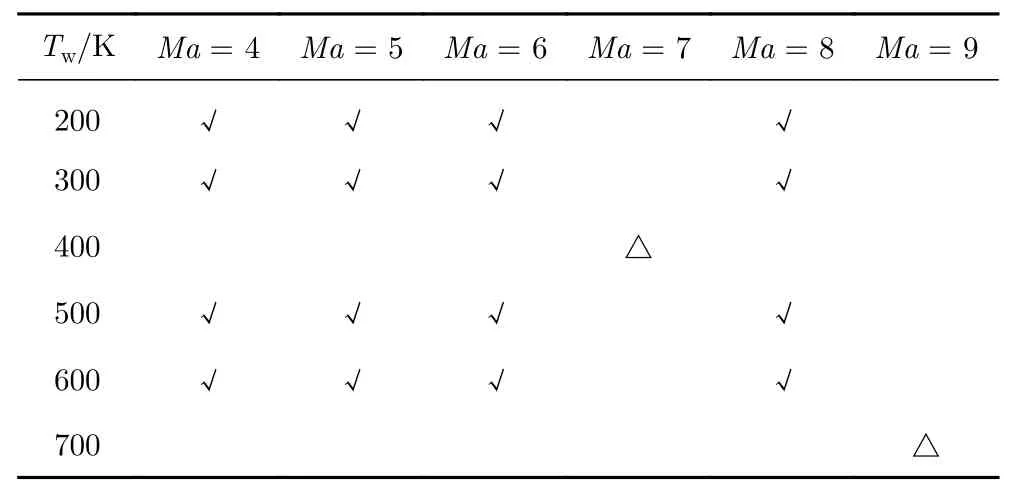
表3 训练和测试状态划分Table 3 Training and test states setting

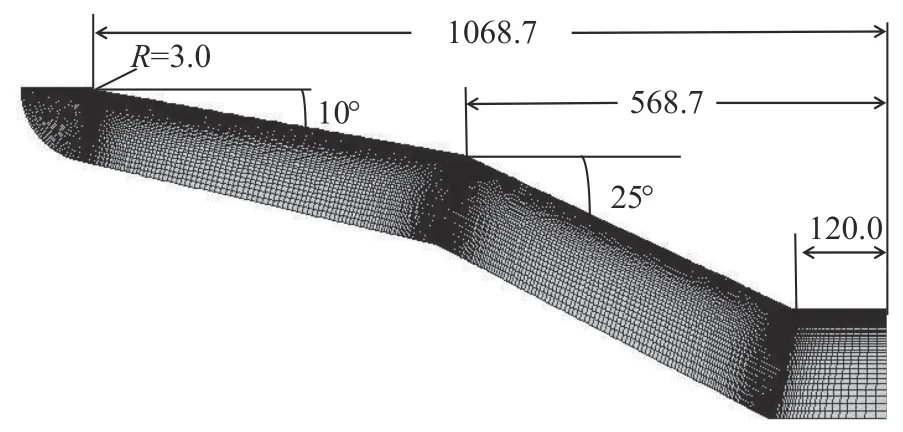
图9 二级压缩面几何尺寸和计算网格（单位：mm）Fig. 9 Geometry dimension and computational grid of the twostage compression surface (unit：mm)

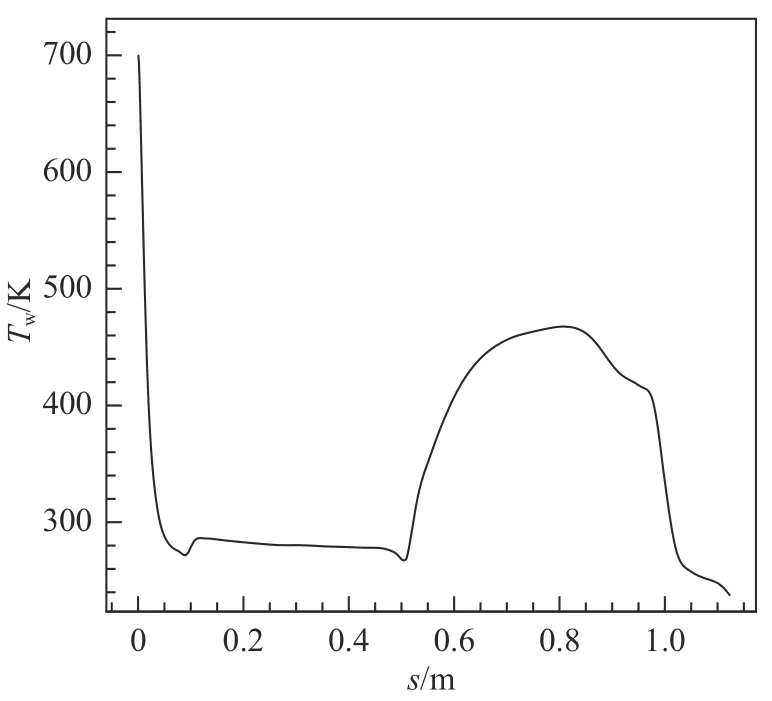
图10 二级压缩面壁面温度分布Fig. 10 Temperature distribution on the two-stage compression surface

在每个状态的二级压缩面上选择78 个点的热流数据和边界层外缘信息。构造候选特征，进行特征选择，得到特征组合完成模型构建，进行模型测试。二级压缩面热流预示结果和RANS 计算结果对比如图11 所示，可以看出，热流预示值和RANS 计算值基本吻合。二级压缩面上一些监测点的热流预示值与RANS 计算值的对比结果如表4 所示，相对误差均小于5%。由以上结果可知，BSLM 方法可以较为精确地进行气动热预示，适用于非均布壁面温度边界条件，且具备对来流马赫数和壁面温度的泛化性。BSLM 气动热预示模型对于非均布壁面温度边界条件的适用能力主要来自该模型的当地性。当地性模型能较为轻松地考虑非均布壁面温度等当地化边界条件，而POD 等方法建立的全局性模型对于当地化边界条件的处理则比较困难。

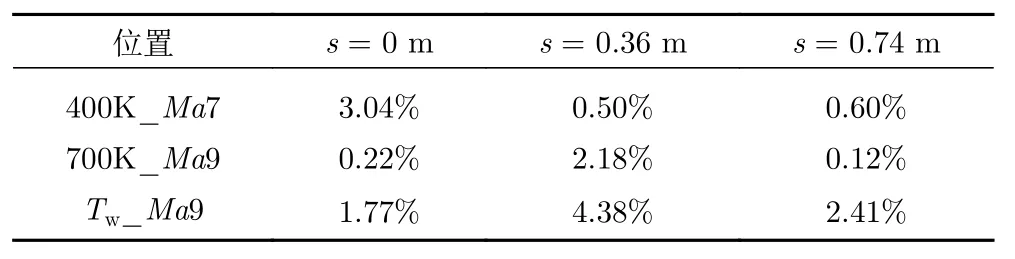
表4 典型位置热流预示值和RANS 计算值相对误差Table 4 Relative error of heat flux at typical locations of the two-stage compression surface between the BSLM prediction and the RANS calculation

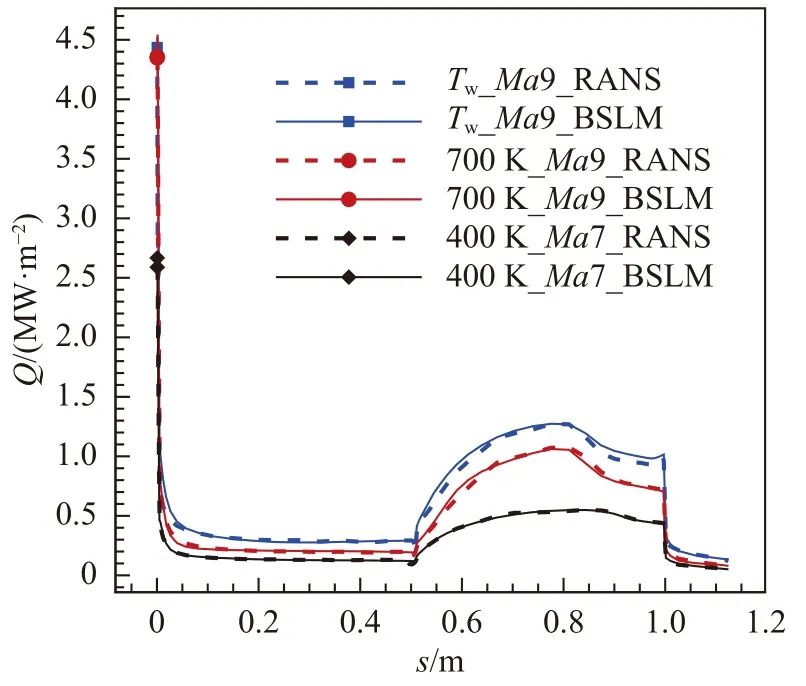
图11 热流预示结果和RANS 计算结果对比Fig. 11 Comparison of heat flux between the RANS calculation and the BSLM prediction

2.4 三维双椭球热流预示

本节使用三维双椭球算例测试BSLM 方法对三维构形的适用性。

以三维双椭球迎角0°、10°、20°和25°作为训练状态，迎角15°作为测试状态，选择双椭球表面的20441个数值模拟网格节点的热流数据和边界层外缘数据进行训练和预示。选择的特征组合为特征θ=tan−1(y/z)，x、y和z为空间坐标。预示结果如图12 所示，图12（a）为RANS 计算的三维双椭球热流分布云图，图12（b）为BSLM 气动热模型预示的三维双椭球热流分布云图。可以看出，气动热模型准确辨识了大椭球头部的高热流区和小椭球头部的次高热流区，并且热流分布与RANS 计算结果基本一致，而且RANS 计算和模型预示得到的驻点热流分别为396.95 kW/m2和401.50 kW/m2，相对误差仅为1.15%。由上述结果可以推断，本文提出的BSLM 气动热预示方法可以较为精确地实现三维构形的气动热预示。

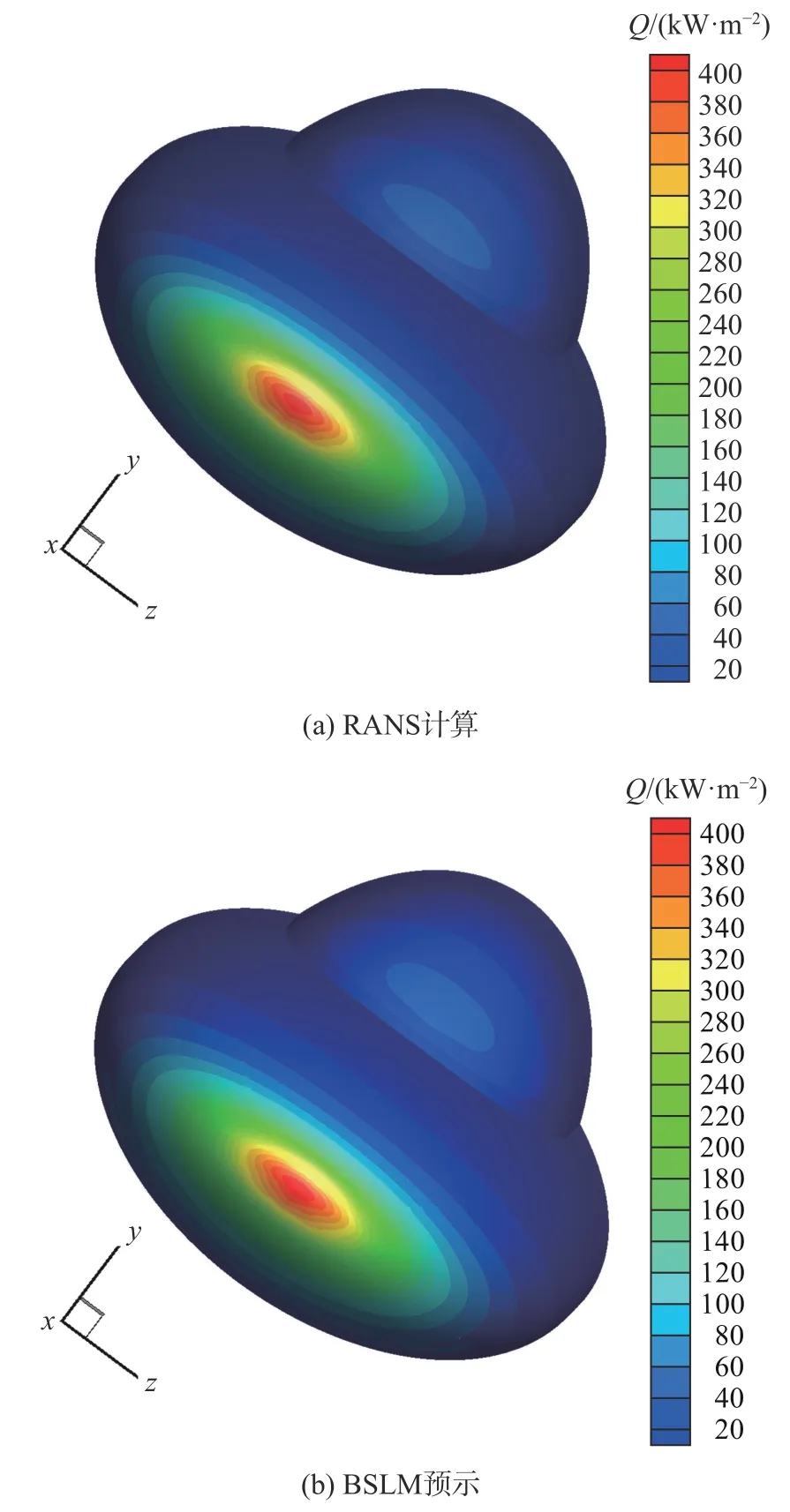
图12 RANS 计算和BSLM 预示的双椭球表面热流分布云图Fig. 12 Heat flux contours on the double ellipsoid surface compared between the RANS calculation and the BSLM prediction

3 结 论

本文针对气动热的高效、高精度预示问题，在Euler 方程计算的边界层外缘信息的基础上，结合少量RANS 结果，使用支持向量机算法发展了一种数据驱动的当地化气动热预示建模方法，实现了不同来流状态、壁面温度下二维及三维构型的气动热高效精准预示。通过双椭球上表面中心线热流预示、二级压缩面热流预示以及三维双椭球热流预示结果验证，可以得到以下结论：

1）气动热预示模型输入特征选择对气动热预示精度有很大的影响，需要事先进行合理的特征选择以保证模型性能。本文所提出的特征选择方法能够筛选出合适的特征组合，使得模型具备较高精度和较好的泛化能力。

2）论文所提出的BSLM 气动热预示方法具有较高的预示精度和良好的泛化性能，热流峰值及典型位置的热流预示结果和数值仿真结果的相对误差均小于5%。

3）BSLM 方法与传统POD 方法相比，可以充分利用边界层外缘信息，具备更高的预示精度，特别是针对热流峰值的预示精度可以提升4 倍以上。另外，由于采用当地化建模策略，实现非均匀壁面温度泛化方面，难度远低于POD 类全局性建模方法。