非结构网格通量重构算法下三种紧致WENO 限制器对比研究

石京昶，严 红，*

(1. 西北工业大学 长三角研究院，太仓 215400；2. 陕西省航空发动机内流动力学重点实验室，西安 710072)

0 引 言

高精度数值格式因日益强烈的工程需求被关注和研究。其中代表性的方法有加权本质无振荡（weighted essentially non-oscillatory, WENO）、间断伽辽金（discontinuous Galerkin methods, DG）、通量重构（flux reconstruction, FR）等。WENO 方法通过非线性重构保证了激波附近“本质无振荡”。DG 和FR 方法天然适用于非结构网格处理复杂几何外形，然而DG、FR 方法本身不能处理激波，所以需要引入限制器。

DG、FR 方法框架下激波捕捉方法的一般思路是：首先采用间断探测器找到需要进行重构的网格单元，然后对目标网格单元采用限制器重构出新的解多项式。如何检测间断有不同的思路，参见Qiu 等的对比研究[1]。其中KXRCF 间断检测器[2]被广泛用于高阶DG 格式的激波捕捉方法研究中。有限体积方法下发展出的TVD、TVB 限制器可以应用于高阶DG、FR 方法，但会丢失高阶方法的高阶特性。WENO 的思想可以用来构造适用于DG 和FR 方法的限制器。Qiu 等[3]和Luo 等[4]提出了Hermite WENO 限制器，但是并不紧致，目标单元解的重构需要用到相邻网格的相邻网格中的解。这种非紧致特性造成DG、FR 方法并行扩展性损失。Zhong 等[5]首先提出了紧致WENO 限制器用于DG 方法，核心思想是将相邻网格单元中的解插值到目标单元，并将单元平均替换为目标单元的单元平均，形成的新多项式与目标单元原本的多项式以WENO 的方式加权平均得到最终的重构多项式解。此WENO 限制器思路清晰，实现简单，故称为简单WENO 限制器（简称SWENO 限制器）。Zhu 等[6-7]在此基础上加以改进，将简单WENO 限制器中目标单元的相邻单元中的解直接插值到目标单元的方式改进为相邻单元中的解通过最小二乘法投影到目标单元。最近，Zhu 等[8-9]又进一步提出了新的多精度WENO 限制器（简称MWENO限制器），其相对于改进的简单WENO 限制器做出的核心改进是，目标单元中的原始高阶多项式分解成从一阶至高阶的多个不同阶次多项式，相邻单元中的解多项式经最小二乘法投影到目标单元，形成一阶多项式后，用于计算最低阶多项式的光滑因子，最终多个不同阶次多项式仍采用WENO 方式加权重构得到最终的解多项式。Li 等[10]也于最近提出了p阶加权WENO 限制器（简称PWENO 限制器）。核心思想与Zhu 等最新的多精度WENO 限制器类似，不过相邻网格单元中的解经最小二乘法投影到目标单元，形成一阶多项式，参与WENO 重构得到最终的解多项式，而不是只用于计算最低阶多项式的光滑因子。以上WENO 限制器在极端低密度低压的局部区域会重构出包含负密度负压的非物理解，因此需要使用保正限制器避免此情形出现。Zhang 等[11]提出的保正限制器能够保持原始高阶精度无损失，被广泛应用于高阶DG 格式激波捕捉方法研究中。但值得一提的是，此保正保精度限制器证明过程中假设单元解点必须是Gauss-Lobatto 点，相比于Gauss-Legendre 点精度较低。

高阶格式计算含有激波的稳态问题时较难收敛到机器零，WENO 格式存在此问题。Zhang 等[12]提出迎风型重构减弱激波后伪振荡。Zhu 等[13]构造了新的多精度WENO 格式。DG 方法结合WENO 限制器激波捕捉同样难以收敛到机器零。最近，Zhu 等[14]提出了一种新的间断探测器，结合其多精度WENO限制器能够在标准算例中获得良好的收敛特性。该间断探测器核心思想是将KXRCF 中基于单元面上解计算差值改为基于单元内解计算差值，本文称之为CKXRCF 间断探测器。

本文在FR 框架下，结合间断探测器和保正保精度限制器，对比研究简单WENO 限制器、p阶加权WENO 限制器和多精度WENO 限制器在多个经典算例中的性能，并讨论其高精度的优势和收敛性问题。常见文献中WENO 限制器验证测试算例集中在无黏Euler 方程，本文将其扩展到激波与层流边界层相互干扰的算例中，针对N-S 方程测试以上WENO 限制器的性能，为相关研究提供初步结果。

1 FR 方法简介

非定常可压缩Navier-Stokes 方程的微分形式可写成如下双曲型守恒律的形式：

式中，通量F(Q)=Fc(Q)−Fv(Q)，守恒变量Q、无黏通量和黏性通量分别如下所示：

本文简介FR 方法二维情形下的基本思想，详细阐述见Wang 等[15]和Huynh 等[16]的综述。计算域离散成N个网格单元{Vi}iN=1。方程（1）的加权弱形式可改写为以下形式：

式中，Qi是网格单元Vi上的近似解，且属于k阶多项式空间，即Qi∈Pk(Vi)。Π[∇·F(Qi)]是∇·F(Qi)在多项式空间Pk上的投影。δi∈Pk(Vi)是Vi上的修正项，由式（3）定义：

式中，W是权函数，[Fn]=Fcnom−Fn(Qi)是网格界面上黎曼通量与单元内部局部通量的差值。将自由度定义在网格单元内部的解点。为计算修正项，在单元界面处定义通量点，则解点上的修正项由式（4）计算：

式中，αj,f,l是独立于解的常数，Sf是单元界面面积，j是解点在当前网格单元内的编号，f是当前网格单元面的编号，l是通量点在当前面的编号。综上所述，FR 方法由以下离散方程近似求解原双曲律方程：

本文所有算例均使用自主开发的N-S 方程非结构网格并行求解器NFR，时间推进方法均采用三阶强稳定性显式SSP-RK3 方法，无黏通量采用Roe 通量或Lax–Friedrichs 通量，黏性通量均采用BR2 格式[17]。本文所有算例的结果均将原始网格单元多项式阶次均等剖分为子单元，如一个四边形网格单元的P2 剖分为4 个四边形子单元。

2 WENO 限制器简介

本文采用的WENO 限制器的基本思路是使用间断探测器找出需要限制解的问题网格单元，然后对其应用WENO 限制器重构得到新解。对于欧拉方程系统，为了更好地避免激波附近的振荡，使用通量雅可比矩阵将守恒变量转换为特征变量，经WENO 限制器重构得到新的特征变量，再经通量雅可比矩阵转换回守恒变量。下述3 种WENO 限制器均只简介其针对一维标量方程的限制过程。

2.1 简单WENO 限制器

简单WENO 限制器的核心是将问题网格单元Ij及其相邻网格单元的解多项式加权组合得到重构解，保证其与原始解有相同的单元平均和k阶精度。权重由解多项式的光滑因子确定。

记网格单元Ij−1、Ij、Ij+1的解为pL(x)、p0(x)、pR(x)，简单WENO 限制器重构的新解为：

式中，ωL、ωR是归一化的非线性权重，(x)、(x)是相邻网格单元内解多项式pL(x)、pR(x)投影到Ij中的新多项式。为保证守恒性，相邻网格单元内的解向Ij中的投影形式为：

式中，单元平均定义为：

注意以上积分均为目标单元Ij内的积分。

上述归一化非线性权重ωl计 算式如下：

式中，

其中，常数ε=1×10−6，r=2。线性权重γL=0.001，γ0=0.998,γR=0.001。光滑因子βl采用经典的WENO方式，定义如下：

2.2 p 阶加权WENO 限制器

记网格单元Ij−1、Ij、Ij+1的解为pL(x)、p0(x)、pR(x)。重构问题网格单元为Ij，其内各阶解多项式p0,s可通过将原始高阶解多项式p0转换为模态多项式获得。为保证守恒性且将相邻网格单元内的线性解多项式投影到问题网格单元，在问题网格单元上可定义来自相邻网格单元Ij−1的线性多项式如下：

来自相邻网格单元Ij+1的线性多项式可通过相似方式得到。

最终的WENO 重构解多项式定义为目标单元内的解与相邻网格单元解的加权组合，保证了和原始解p0有相同的单元平均和k阶精度。

上述归一化非线性权重ωl计算同公式（9），式中ωl计算式如下：

线性权重γl和参数εl与简单WENO 限制器中的不同，不再是常数，而是因为l对应的阶次不同而有区别，设定如下：

式中，参数Kε取0.01。

显然，线性权重γl和参数εl对 阶次的依赖关系弱化了相邻网格单元Ij±1内的解投影到目标网格单元Ij中的线性多项式，强化了Ij中的高阶模态。另外，当低阶模态的振荡程度比高阶模态更严重时，令低阶模态的线性权重为0，去掉振荡程度更严重的部分模态。按照如下平均方式比较两者的光滑因子：

式中，参数Ktrunc常取1，τs,r是多项式p0,s的光滑因子βs的分量，即因此，计算光滑因子βs时存储τs,r留待此处使用。方程（19）中右端高阶模态的光滑因子平均值对每个s阶模态是变化的。令s从最高阶k降序至2，对每个s检查；如果低阶模态的光滑因子平均值更大，则令高阶模态之外的模态多项式对应的线性权重为0。

2.3 多精度WENO 限制器

记网格单元Ij−1、Ij、Ij+1的解为pL(x)、p0(x)、pR(x)。重构问题网格单元为Ij，其内各阶解多项式p0,s可通过将原始高阶解多项式p0转换为模态多项式获得。基于各阶解多项式重构得到新的线性解多项式p和非线性解多项式p˜。

上述非线性权重ωl1,l2计算如下：

式中，光滑因子β0,1的计算并不依赖于零阶多项式p0,0，而是依赖相邻网格单元中重构得到的多项式：

式中，σL、σR为相邻网格单元重构解的光滑因子。为保证守恒性，且将相邻网格单元内的线性解多项式投影到目标单元，在目标单元上可定义来自相邻网格单元Ij−1的线性多项式如下：

来自相邻网格单元Ij+1的线性多项式用相似方式得到。

最终的WENO 重构解多项式定义为最高k阶非线性解多项式，保证了和原始解p0有相同的单元平均和k阶精度。

2.4 保正保精度限制器

尽管前述限制器抑制了FR 方法在激波附近的振荡，但无法完全避免出现负密度和压力，限制器对解多项式的重构并不考虑是否会重构出非物理的解。因此还需要保正保精度限制器配合激波捕捉方法。本文实现的保正保精度限制器[11]要求使用Legendre-Gauss-Lobatto 点，以保证采用显式RK 时间推进格式和一定的CFL（Courant-Friedrichs-Lewy）数下，可以从数学上证明该限制器保正保精度且守恒。记目标网格单元为Ij，k阶多项式解分布在N(k)个Legendre-Gauss-Lobatto 点上，记守恒标量qj,i、密度ρ j,i、压力pj,i，i∈[1,N(k)]，ε=1×10−15表征极小的正值。保正保精度限制器的算法流程如下：

1）限制密度。找出当前网格单元所有解点上密度ρ j,i的最小值，若该值小于允许的最小正值ε，则将该网格单元中所有解点上的密度ρ j,i等比例缩小。

本文所有算例均使用了保正保精度限制器。

3 间断探测器简介

3.1 KXRCF 间断探测器

记网格单元Ij−1、Ij、Ij+1的解为pL(x)、p0(x)、pR(x)。将网格单元Ij的所有面分为两组：流入面组∂I−j和流出面组∂I+j，则可由如下条件判断间断：

其中，m=1，Ck=1，hj是网格单元Ij的特征半径。公式（33）的物理含义是，如果该网格单元与相邻网格单元在“流入面组”上的间断差值占比超过了Ck值，就判定其为问题网格单元。

3.2 CKXRCF 间断探测器

记网格单元Ij−1、Ij、Ij+1的解为pL(x)、p0(x)、pR(x)。先计算目标网格单元及其相邻网格单元内解的积分，再由其差值判断间断。具体如下：

其中，Ck=1，hj是网格单元Ij的特征半径。CKXRCF间断探测器与KXRCF 间断探测器的不同在于前者使用了单元内解的积分，而非网格单元交界面通量点处解的积分。一般来说，流场中存在间断时，高阶解多项式在相邻网格单元中存在振荡，而且在网格单元内积分的振荡比网格单元界面处积分的振荡小，有利于保持稳定地探测包含间断的网格单元，有利于稳定收敛。这一特性也将在后续算例讨论中得到验证。

4 算例结果及讨论

4.1 双马赫反射

双马赫反射算例是验证高精度激波捕捉格式的经典算例[18]。控制方程为欧拉方程，计算域为[0,4]×[0,1]。初始条件为下表面x=1/6处一道右行激波Ma=10，与x轴夹角为60°。x=1/6之后下边界为滑移壁面，上边界变量随时间变化与右行激波匹配，右边界为超声速出流边界。计算时间为0～0.2。模拟采用三阶空间精度P2 和Roe 通量，基于均匀分布的四边形网格中Legendre-Gauss-Lobatto 积分点。

图1～图3 显示了SWENO、PWENO 和MWENO限制器P2 在三组网格上的密度云图结果，图中蓝色线是[1.75, 21.5]范围内均匀分布的30 条密度等值线，红色表示t= 0.2 时当地网格单元被KXRCF 间断探测器标记为问题网格单元。对比显示PWENO 限制器和MWENO 限制器均能在较细的网格上获得清晰的涡结构，SWENO 限制器则分辨率较差且数值噪声较大。SWENO 限制器从相邻网格单元中直接取多项式替换单元平均，这显然是其存在较强数值振荡的直接原因。PWENO 限制器与MWENO 限制器表现类似。PWENO 限制器对涡的分辨率更高，但在上游区域的数值噪声相对较大。PWENO 限制器与MWENO限制器的基本思路都是将目标网格单元内的高阶多项式与相邻网格单元的低阶多项式加权组合，所以表现相似。PWENO 限制器存在可调的参数用于控制数值耗散，而MWENO 限制器基本没有可调参数。PWENO 限制器在当前参数Ktrunc=1、Kε=0.01下，数值耗散较小，因此对涡的分辨率相对更高，但同时造成数值噪声更明显。

图1 SWENO 限制器P2 在三组网格上的密度云图Fig. 1 Contour of density on 3 grids using SWENO limiter P2

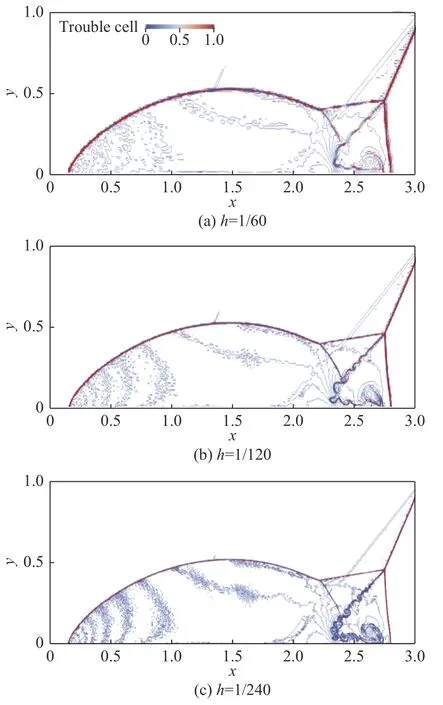
图2 PWENO 限制器P2 在三组网格上的密度云图Fig. 2 Contour of density on 3 grids using PWENO limiter P2

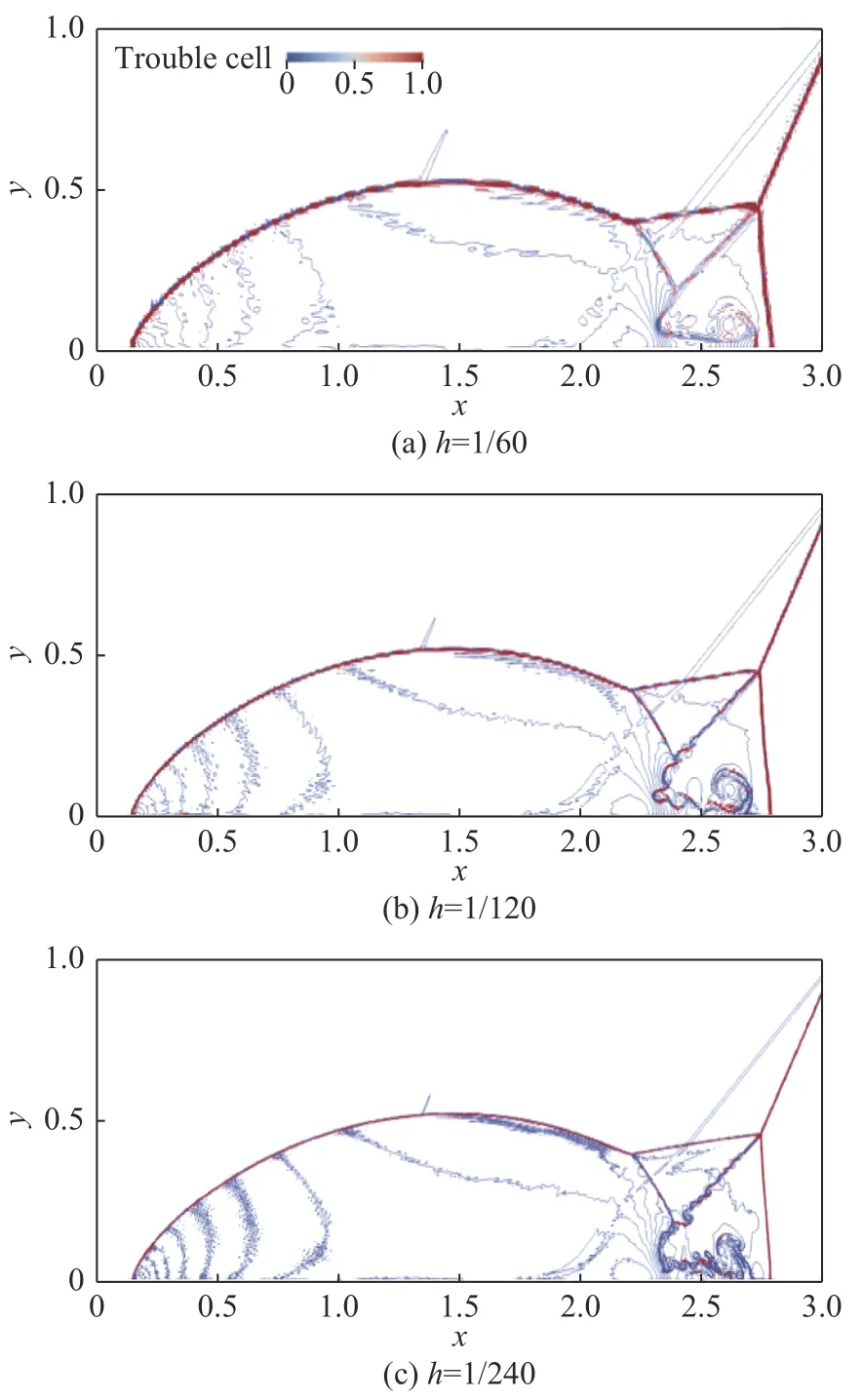
图3 MWENO 限制器P2 在三组网格上的密度云图Fig. 3 Contour of density on 3 grids using MWENO limiter P2

4.2 激波与涡相互作用

激波与涡相互作用算例在第五届高阶CFD 国际研讨会上用来检验高阶激波捕捉格式预测强涡与激波相互作用的复杂现象[19]。这是一个二维非定常无黏流内含激波造成的间断。涡传播过程中遇到激波后，激波结构会出现显著畸变，随之产生多道向下游传播的波。在这个过程中存在两种物理现象：第一个流动特征是初始的涡通过激波时由于压缩效应分裂成两个涡结构，激波下游的涡结构依赖于激波与涡的相对强度；第二个流动特征是激波下游的波结构反射传播。本文采用的计算域及设定来自第五届高阶CFD 国际研讨会，网格为研讨会提供的网格RQ300，细节见第五届高阶CFD 国际研讨会[19]。模拟采用四阶空间精度P3 和Roe 通量，基于均匀分布的四边形网格中的Legendre-Gauss-Lobatto 积分点，PWENO 限制器参数Ktrunc=10、Kε=0.01。

在这一算例中，SWENO 中途崩溃，故未显示结果。图4 显示了MWENO 和PWENO 限制器P3 的数值纹影云图。图4（a）中红色显示了KXRCF 间断探测器中的参数Ck=0.01时标记的问题网格单元，即KXRCF 间断探测器只标记了激波，没有标记激波下游存在数值伪振荡的区域为问题网格单元。对比图4（a、b）中的结果显示，对整个计算域应用PWENO限制器后，激波下游的数值伪振荡明显减弱，即PWENO 限制器抑制了FR 格式本身在激波附近的数值伪振荡。同时也应看到，如图5 所示，涡核分裂核心区域的流场结构没有受到数值伪振荡的明显影响。图4（c）显示了在所有网格单元应用MWENO 限制器后得到的数值纹影。对比图4（b、c）的结果显示，相比PWENO 限制器，MWENO 限制器在激波下游区域的数值伪振荡更加明显。

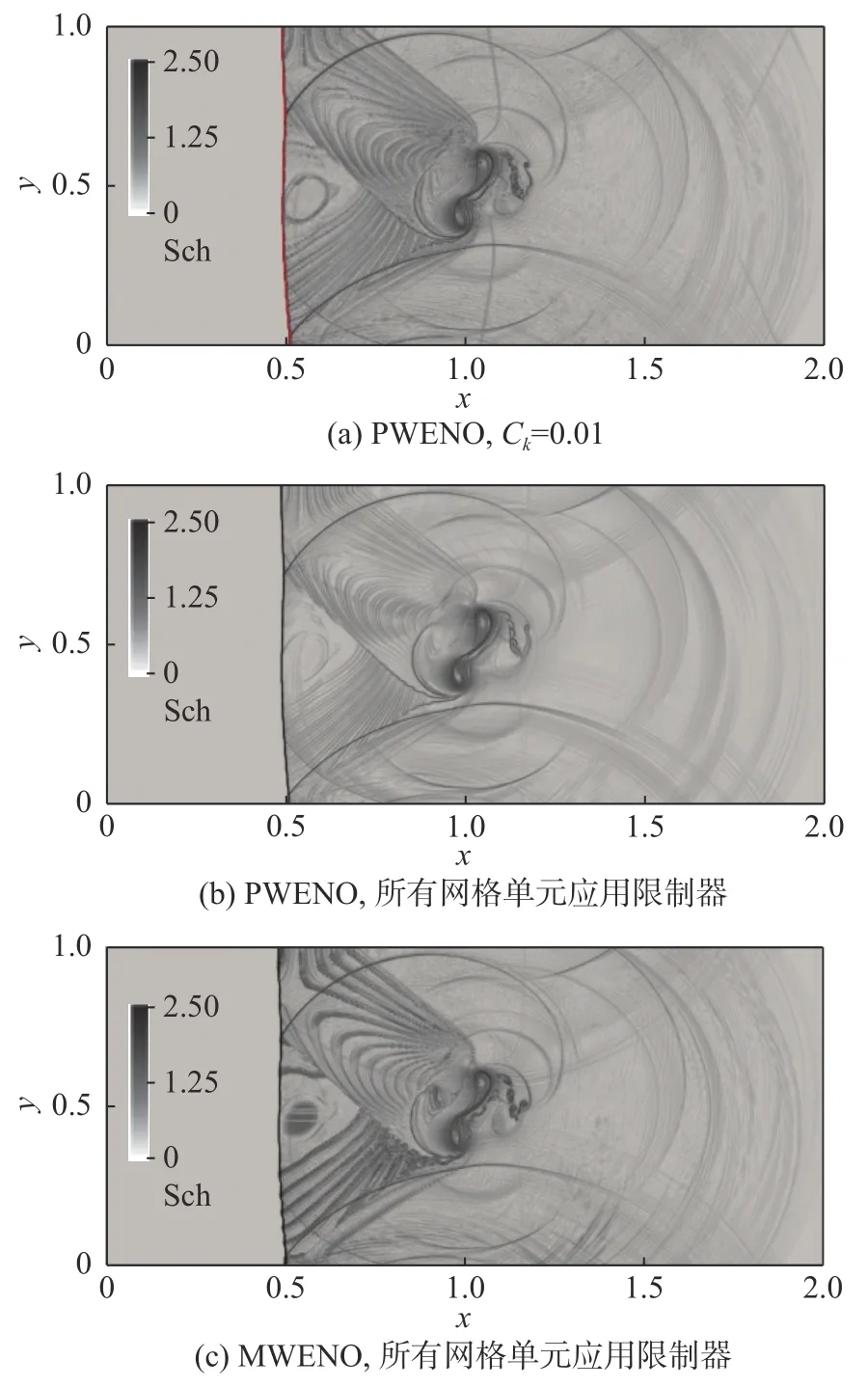
图4 PWENO 和MWENO 限制器P3 的数值纹影云图Fig. 4 Contour of numerical schlieren using PWENO and MWENO limiter P3

图5 核心涡核分裂区PWENO 限制器P3 数值纹影云图Fig. 5 Contour of numerical schlieren in the core region usingPWENO limiter P3

4.3 激波反射

激波反射算例[14]用来测试激波捕捉格式对稳态激波问题的收敛能力。该二维问题的计算域定义为[0,4]×[0,1]。初场设定为(ρ,u,v,p)=(1.0,2.9,0,1.0/1.4)。边界条件设定如下：计算域下边界为无黏壁面；右边界为超声速出流边界；左边界设为Dirichlet 边界条件，(ρ,u,v,p)=(1.0,2.9,0,1.0/1.4)；上边界设定为Dirichlet边界条件，有(ρ,u,v,p)=(1.699 97, 2.619 34, −0.506 32,1.528 19)。二维数值模拟到收敛，检查数值解与无黏激波关系式导出的解析解之间的误差。模拟基于三套连续加密的四边形网格，采用Lax–Friedrichs 通量；基于四边形网格中Legendre-Gauss-Lobatto 积分点；PWENO 限制器参数Ktrunc=10、Kε=0.01；时间推进从初场模拟到密度残差收敛到1×10−12。粗、中、细3 套网格单元数目依次为：120×30、240×60、480×120。

图6 （a）显示了细网格P2 采用PWENO 限制器得到的压力等值线和CKXRCF 间断探测器标记的红色问题网格单元，从中可以看到CKXRCF 间断探测器精准探测了激波所在的网格单元，没有标记非激波区域。密度残差收敛后，提取位于y= 0.5 上的压力。3 套连续加密网格上P2 的压力分布如图6（b）所示，精确解根据正激波关系式计算得到。对比连续加密网格上的压力分布发现，激波下游附近存在振荡，但随着网格加密，振荡迅速变弱，且激波下游存在明显振荡的网格数目明显减少。

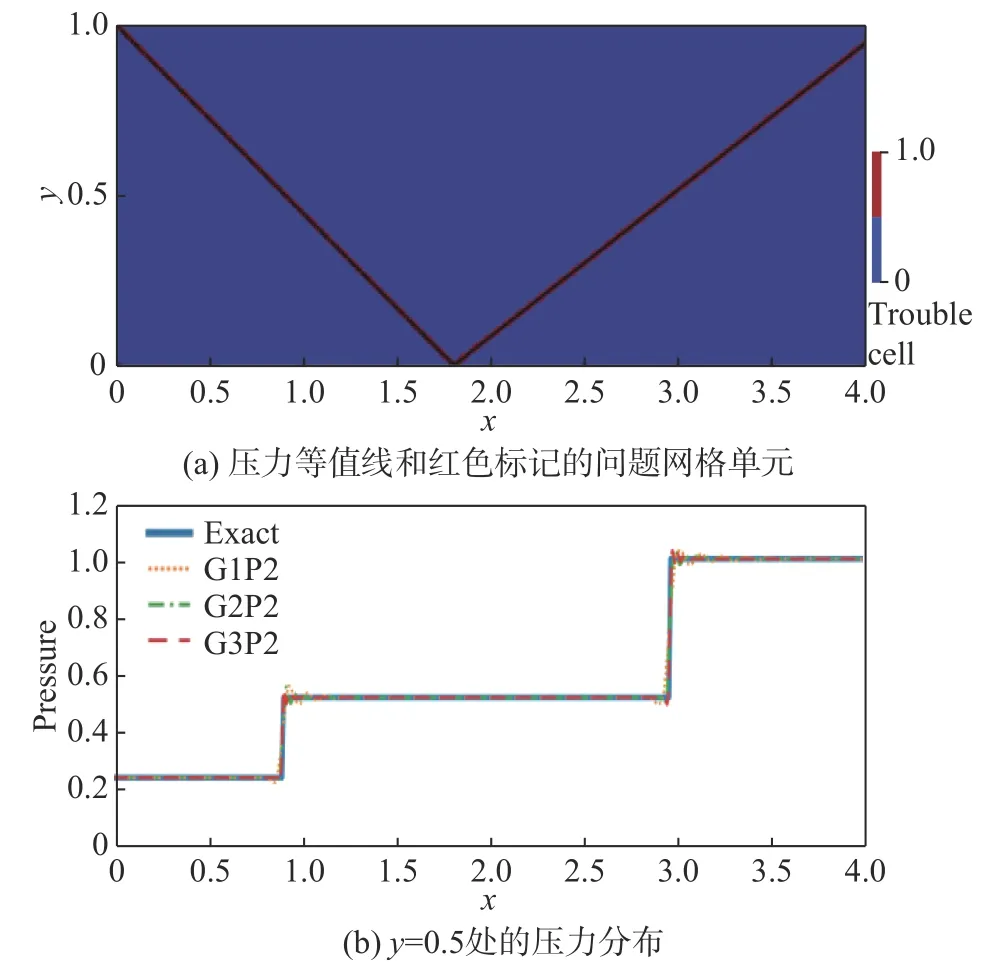
图6 PWENO 限制器P2 在细网格上的压力等值线图、y =0.5 处压力分布和CKXRCF 间断探测器标记的问题网格单元Fig. 6 Pressure contour and pressure distribution at y = 0.5 using PWENO limiter P2 with contour of troubled cell by CKXRCF shock sensor

图7 显示了SWENO、PWENO 和MWENO 限制器在CKXRCF 间断探测器下的收敛特性及其在y=0.5 处的压力分布。图7（a）中PWENO 限制器在不同的间断探测器下表现不同：采用的KXRCF 间断探测器无法收敛；采用的CKXRCF 间断探测器可以收敛；MWENO 限制器配合CKXRCF 限制器也可以收敛；但即使应用CKXRCF 限制器，SWENO 限制器也无法收敛。在定常激波反射这一算例中，图7（a）中无法收敛的特性没有对图7（b）中的y= 0.5 处压力分布造成明显影响。SWENO、PWENO、MWENO 限制器在激波附近均存在一定程度的数值振荡。

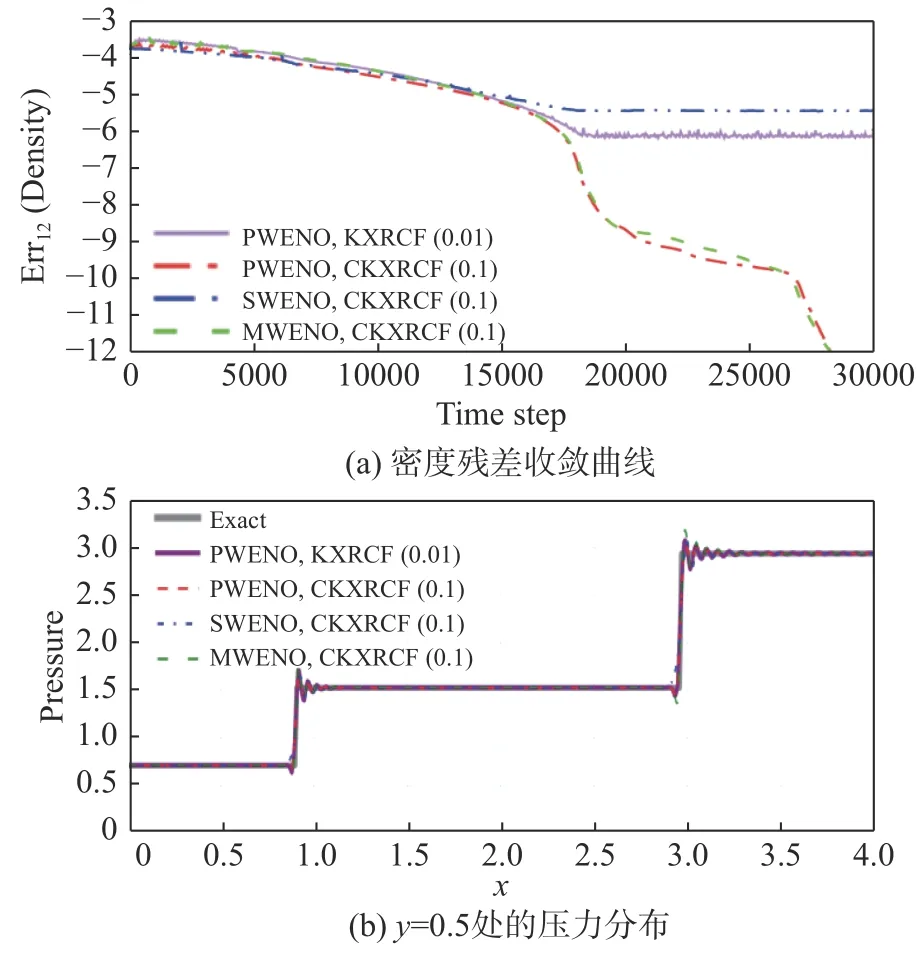
图7 SWENO、PWENO 和MWENO 限制器P2 在中网格上使用不同间断探测器的密度残差收敛曲线及y = 0.5 处压力分布Fig. 7 History of density residual and pressure distribution at y = 0.5 of SWENO, PWENO, MWENO limiter P2 on medium grid with different shock sensors

4.4 黏性弓形激波

弓形激波是验证激波捕捉格式的经典算例，脱体激波可以尽量隔绝边界条件的影响来验证激波捕捉格式, 同时稳态激波用来检验高阶激波捕捉格式的收敛特性。黏性弓形激波算例在检验激波捕捉格式的同时还对数值格式解析高超声速下很薄的边界层提出了较高要求。该问题中的几何构型是一个半圆柱，自由来流Ma=8.03，基于圆柱半径的雷诺数Re=1.835×105。虽然几何构型对称，但仍然保留整体构型以检验高阶格式是否会产生伪波动。计算域不包括钝体下游部分，避免出现非定常尾迹区。初场设定为自由来流。边界条件设定如下：来流边界为自由来流的 Dirichlet 边界条件，出流边界为外插边界条件，圆柱壁面为黏性绝热壁面。模拟基于3 套连续加密的四边形网格，采用三阶空间精度P2 和Lax-Friedrichs 通量，基于四边形网格中Legendre-Gauss-Lobatto 积分点，PWENO 限制器参数Ktrunc=10、Kε=0.01，时间推进从初场模拟到密度残差收敛到1×10−10。三套网格均设定为：沿壁面均匀分布，在壁面法向方向上自壁面向自由来流边界拉伸，靠近圆柱壁面附近的拉伸比为1.05，靠近自由来流边界附近的拉伸比为2。粗、中、细3 套网格单元数目依次为：34×45、68×65、136×95。

在这一算例中，SWENO 中途崩溃，故未显示结果。图8 显示了PWENO 限制器P2 的收敛结果。图8（a）显示了在细网格的所有网格单元中应用PWENO 限制器P2 的压力云图。压力进行了归一化处理：p/p02，其中p02是根据激波关系式计算得到的滞止点处的压力。3 套连续加密网格中，圆柱壁面上PWENO 限制器P2 的压力分布如图8（b）所示。实验数据提取自 Wieting[20]的实验，参考数值模拟结果提取自Jiang 等[18]的DG/FV 混合格式结果。结果表明，网格加密后PWENO 限制器P2 在圆柱壁面上的压力分布收敛到了参考的数值结果。

图8 PWENO 限制器P2 在细网格上的压力云图和3 套网格上的壁面压力分布Fig. 8 Pressure contour and the converged wall pressure distribution using PWENO limiter P2

图9 显示了PWENO 和MWENO 限制器的收敛特性及壁面压力分布。图9（a）中PWENO 限制器在不同的间断探测器下表现不同：采用的KXRCF 间断探测器和采用的CKXRCF 间断探测器均无法收敛；全场应用PWENO 限制器可以收敛；但即使全场应用限制器，MWENO 限制器也无法收敛。图9（a）中无法收敛的特征与图9（b）中的壁面压力分布是对应的。PWENO 限制器在KXRCF 和CKXRCF 间断探测器下无法收敛是中轴线处数值振荡导致的，MWENO 限制器无法收敛则是出口边界附近的数值振荡导致的。

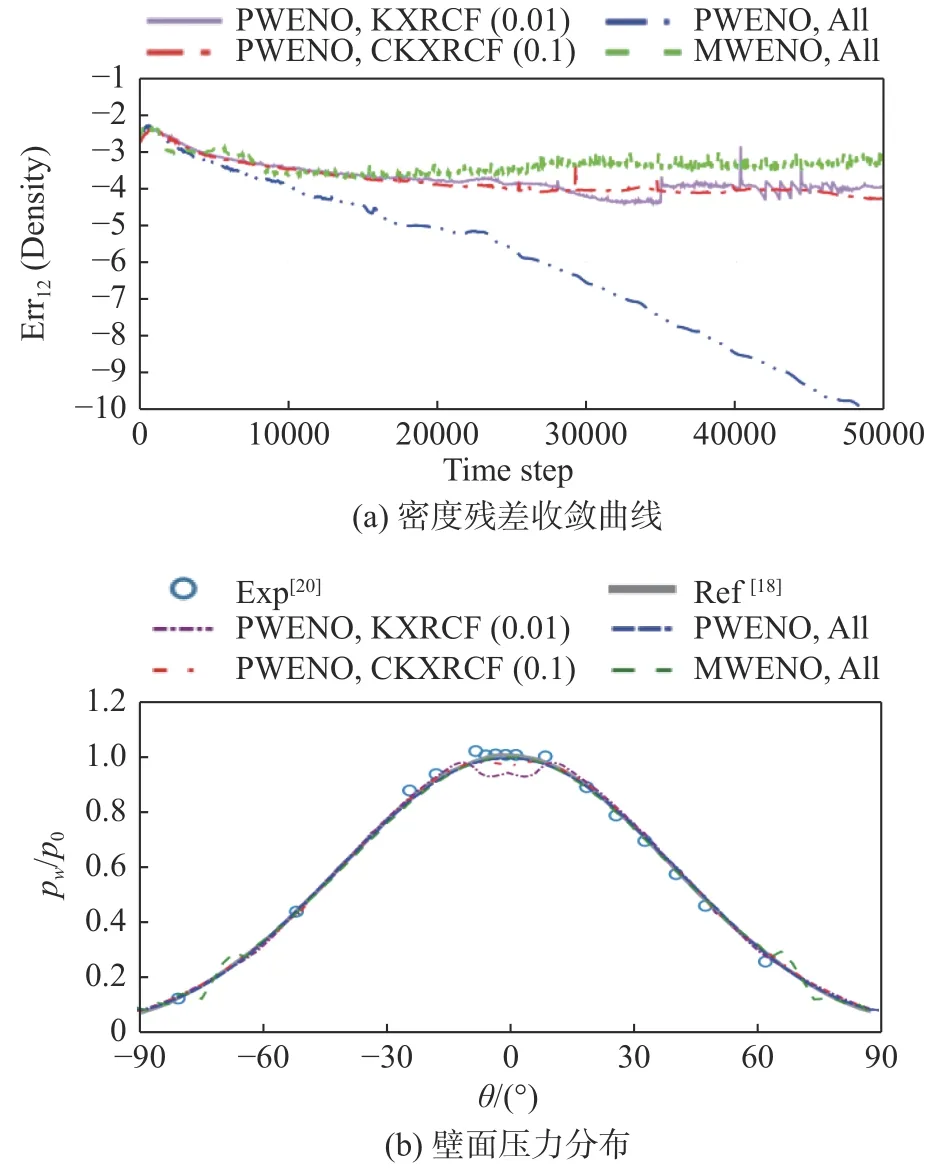
图9 PWENO 和MWENO 限制器P2 在粗网格上使用不同间断探测器的密度残差收敛曲线及壁面压力分布Fig. 9 History of density residual and wall pressure distribution of PWENO, MWENO limiter P2 on coarse grid with different shock sensors

4.5 激波与层流边界层相互作用

二维激波与层流边界层相互作用[21]用以检验激波捕捉格式模拟入射激波与平板层流边界层相互作用。入射激波与层流边界层相互作用，导致流动分离并产生分离泡。计算域为[−0.2,2]×[0,1]，对层流边界层的模拟包含前缘。自由来流Ma∞=2.15，基于激波入射点位置的雷诺数Re=ρ∞U∞xsh/µ∞=1×105，激波入射点位于xsh=1处。入射激波与x轴之间的夹角θ= 30.8°。激波入射通过设定边界条件实现。在y=1.2tanθ处将入口边界分为上、下两段。下段y＜1.2tanθ设定为无攻角的自由来流，Ma∞=2.15；上段y＞1.2tanθ设定为带攻角的来流，其流动参数与自由来流之间满足Rankine-Hugoniot 关系。其余边界条件设为：上边界为远场自由来流边界，参考状态同入口边界上段；右边界为外插边界条件；下边界上游x＜0部分为对称面，下游为平板无黏绝热壁面。初场设定为自由来流Ma∞=2.15的状态。模拟基于三套连续加密的四边形网格，采用三阶空间精度P2 和Lax–Friedrichs 通量，基于四边形网格中Legendre-Gauss-Lobatto 积分点，PWENO 限制器参数Ktrunc=10、Kε=0.01，时间推进从初场模拟到密度残差收敛到1×10−12。三套网格均设定为在壁面法向方向上自壁面向远场边界拉伸，靠近壁面附近的拉伸比为1.05，靠近远场边界附近的拉伸比为2；在壁面切向方向上自激波入射点向上下游拉伸。粗、中、细3 套网格单元数目依次为：76×32、130×47、154×54。

在这一算例中，SWENO 中途崩溃，故未显示结果。图10 显示了PWENO 限制器P2 的收敛结果。图10（a）显示了在细网格的所有网格单元中应用PWENO 限制器P2 的密度云图，密度进行了归一化处理：ρ/ρ∞，其中ρ∞是自由来流的密度。三套连续加密网格中，壁面上PWENO 限制器P2 的Cf分布如图10 （b）所示。参考数值模拟结果提取自第四届高阶CFD 国际研讨会上的总结报告[22]，其采用DG 在11041 个网格单元上进行P6 模拟得到收敛解。结果表明，网格加密后PWENO 限制器P2 在壁面上的Cf分布收敛到了参考的数值结果。

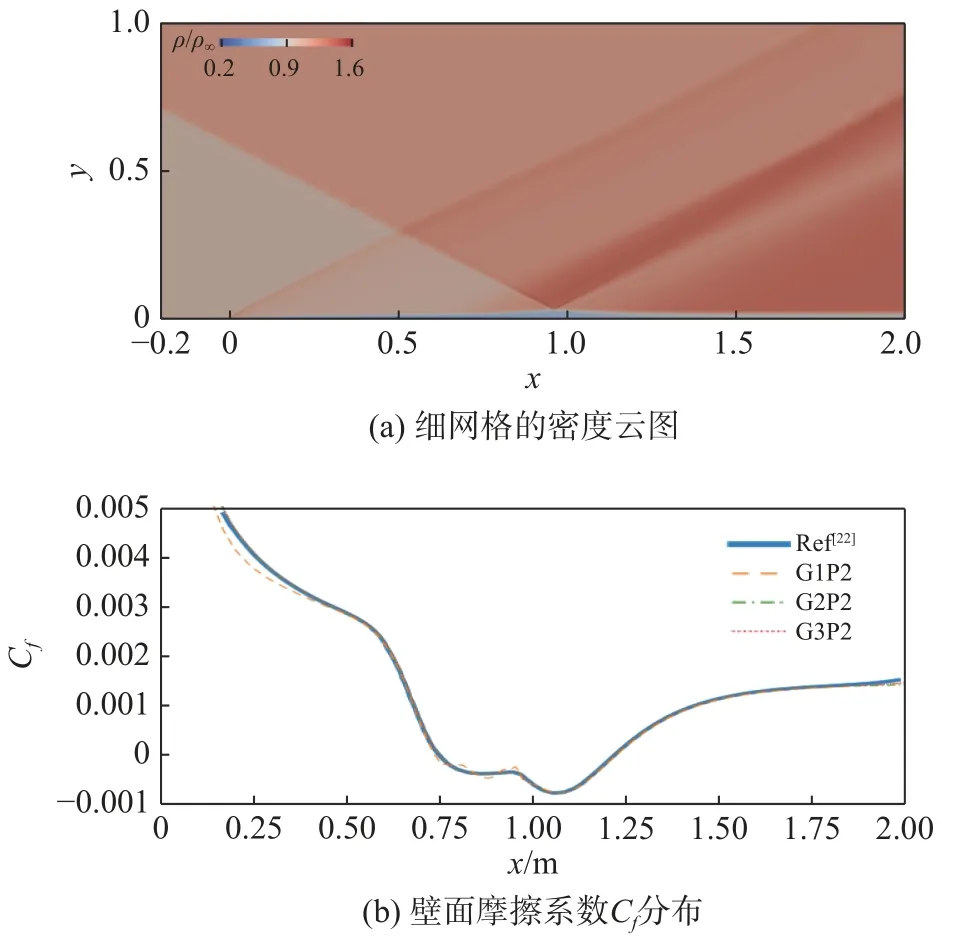
图10 PWENO 限制器P2 在细网格上的密度云图和3 个网格上的 Cf曲线Fig. 10 Density contour on grid 3 and Cf distribution of PWENO limiter P2 on refined grid

图11 显示了PWENO 和MWENO 限制器的收敛特性及其壁面分布。图11（a）中PWENO 限制器在不同的间断探测器下表现不同：采用的KXRCF 间断探测器无法收敛；采用的CKXRCF 间断探测器逐渐趋向收敛，但存在振荡；全场应用PWENO 限制器可以收敛；全场应用限制器，MWENO 限制器也可以收敛。图11（a）中无法收敛的特征对图11（b）中的壁面分布影响不大，只有CKXRCF 间断探测器的“振荡式”收敛对应壁面前半部分的较小偏差。

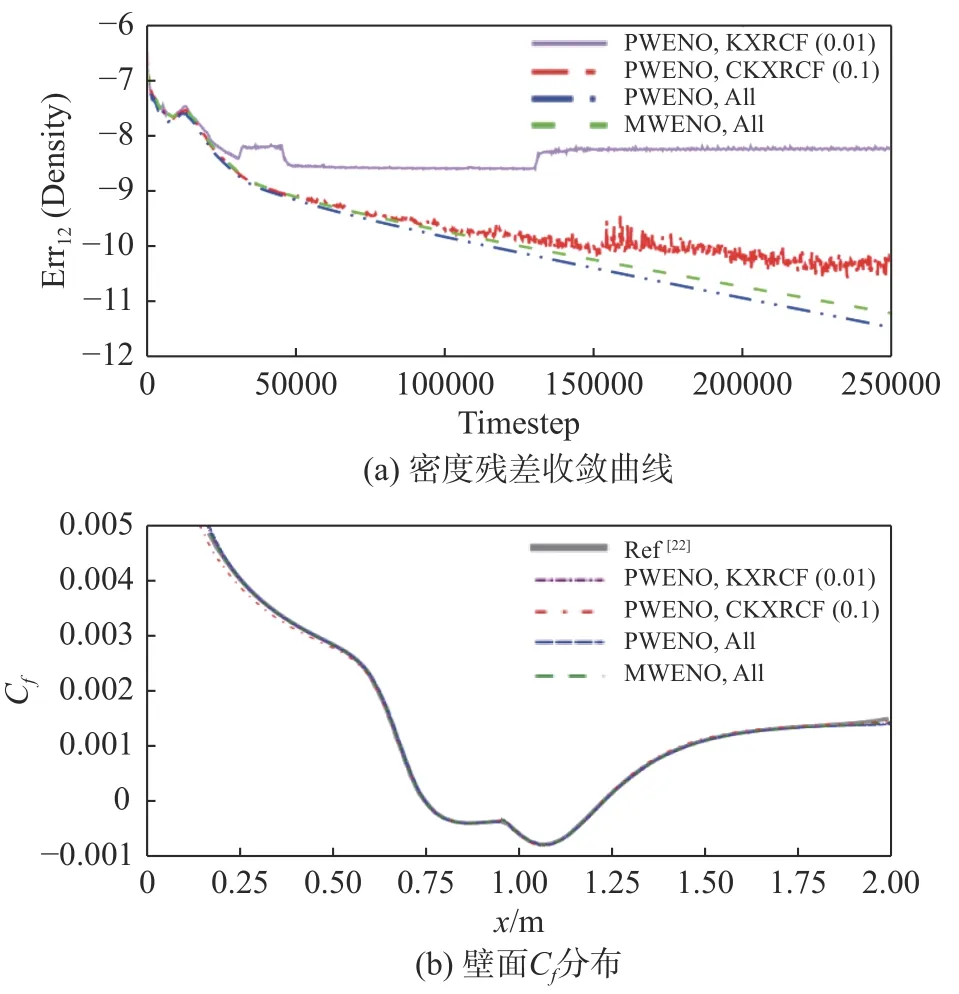
图11 PWENO 和MWENO 限制器P2 在中网格上使用不同间断探测器的密度残差收敛曲线及壁面压力分布Fig. 11 History of density residual and wall friction distribution of PWENO, MWENO limiter P2 on medium grid with different shock sensors

5 结 论

本文通过在FR 方法框架下对比研究简单WENO限制器、p阶加权WENO 限制器和多精度WENO 限制器在多个二维无黏及黏性算例中的性能表现。确认简单WENO 限制器性能较差，多精度WENO 限制器与p阶加权WENO 限制器性能相似，捕捉激波的解析精度较高，而且能够一定程度地抑制FR 格式本身在激波附近的数值伪振荡。与多精度WENO 限制器相比，p阶加权WENO 限制器的稳态收敛性相对更好。虽然本文研究的多个算例中全场应用WENO限制器可以得到收敛的结果，但多精度WENO 限制器和p 阶加权WENO 限制器均亟需设计新型的间断探测器避免限制光滑区域，以减少计算量并保证收敛。