WENO 格式的一种新型光滑因子及其应用
刘旭亮,武从海,李 虎,范召林
(1. 空气动力学国家重点实验室,绵阳 621000;2. 中国空气动力研究与发展中心,绵阳 621000)
0 引 言
双曲守恒方程是流体力学领域基本控制方程之一,在特定物理参数下,即使初始条件是光滑的,也可能出现激波和接触间断等不连续解,采用传统的线性格式进行数值求解会导致虚假振荡。准确模拟该类方程中的间断及精细结构需要开展非线性激波捕捉方法研究,为此,许多学者建立了一系列理论和方法。
为了消除间断处的数值振荡,Godunov[1]在1959 年首次提出迎风格式的思想,这是一个里程碑性的近似解方法。后来,Harten[2-3]建立了总变差递减(total variation diminishing, TVD)格式。Godunov 格式仅有一阶精度,TVD 格式在数学上已经被证明至多能达到二阶精度[4]。为了抑制数值解在激波上、下游的振荡,同时保证熵增条件,张涵信[5]提出了一种无波动、无自由参数的耗散差分算法,即二阶精度的NND 格式。 由于 NND 格式具有TVD 性质,物理概念明确且形式简洁,在工程领域得到了广泛的应用。随后,张涵信及其团队进一步发展了三阶精度的ENN 格式[6]。为了进一步提高精度,Harten 等[7-9]通过放宽TVD 条件,提出了有限体积框架的本质无振荡(essentially non-oscillatory, ENO)重构格式。ENO 格式采用Newton 差商作为光滑因子,其基本思想是选择Newton 差商较小的候选模板来进行重构,从而达到一致高阶精度,并且在间断和局部极值点附近具有本质无振荡的性质。之后,Shu 和Osher[10-11]将ENO 格式推广到了有限差分框架。
ENO 格式在重构过程中计算了多个候选模板的光滑因子,但最后只选择了最光滑的一个模板进行重构。在间断区域,ENO 格式的思想是十分成功的;但是在光滑区域,从多个光滑候选模板中只选择最光滑的模板则未充分利用其余候选模板的信息。为了把多个光滑模板都利用起来并且提高格式精度, Liu等[12]在1994 年基于ENO 格式发展了有限体积框架的加权ENO(weighted ENO, WENO)格式。WENO格式把所有候选模板以凸组合的方式进行非线性加权,从而实现了一致高阶精度,并且保持了间断附近的本质无振荡性质。非线性权值分配的基本策略是在光滑区域恢复到最优精度的迎风格式,在间断模板分配较小的权值,实现本质无振荡的性质。由于Liu 等[12]的WENO 格式采用Newton 差商的平方和作为光滑因子,导致WENO 格式在光滑区不能达到最优精度[13],例如五点WENO 格式在光滑区只能达到四阶精度。1996 年,Jiang 和Shu[14]将WENO 格式推广到了有限差分框架(简称为WENO-JS 格式),这项工作更重要的是通过所有候选模板的子重构多项式导数的归一化平方和(L2范数)构造了Jiang-Shu 光滑因子。由于该光滑因子的良好特性,使得五点WENO-JS 格式在光滑区能达到五阶最优精度。随后的研究者[15-17]基于Jiang-Shu 光滑因子得到了更高阶的WENO-JS 格式,并将其应用到求解间断和复杂流动问题。
Henrick 等[18]对五阶WENO-JS 格式进行研究,结果表明当存在高阶临界点(critical points)时,五阶WENO-JS 格式的收敛精度会降至三阶甚至更低。为了修正这一缺陷,Henrick 等[18]巧妙设计了一个映射函数,对WENO-JS 格式的非线性权进行映射,使得非线性权在光滑区尽可能接近线性权。该格式被称为映射WENO(mapped WENO)格式,简称WENOM 格式。相比于WENO-JS 格式,WENO-M 格式可以在光滑区域的临界点达到最优收敛精度,同时降低数值耗散。Borges 等[19]通过对子模板上的Jiang-Shu 光滑因子进行线性组合,提出了全局光滑因子,他们将全局光滑因子与局部光滑因子之比引入到非线性权的设计中,称为WENO-Z 格式。五阶WENO-Z 格式在一阶临界点处能达到最优收敛精度,并且由于WENO-Z 格式不需要计算映射函数,使得WENOZ 格式计算效率高于WENO-M 格式。随后,Castro等[20]发展了高阶WENO-Z 格式,给出了所有奇数阶精度的全局光滑因子的公式。WENO-M 和WENOZ 格式在子模板上依然采用的是Jiang-Shu 光滑因子,本质上都是导数项的L2范数。如果基于L1范数设计光滑因子,则可能会在光滑区域丢失精度[21]。为了克服这个缺陷,Ha 等[22]通过控制Taylor 展开余项来构造L1范数意义下的局部和全局光滑因子,然后采用WENO-Z 型非线性权得到满足最优精度的WENO 格式,简记为WENO-NS 格式。Ha 等[22]验证了存在一阶临界点时,五阶WENO-NS 格式依然能达到最优精度。然而,WENO-NS 格式的光滑因子存在不对称性,并且全局光滑因子的计算量比较大,随后的研究工作[23-25]针对这些问题进行了改进。WENO格式计算量最大的部分在于光滑因子,为了降低计算成本,Baeza 等[26]构造了一类高效计算的光滑因子,其形式比Jiang-Shu 光滑因子更简洁,计算效率更高。基于该光滑因子,通过WENO-Z 型非线性权得到了满足最优精度的快速WENO(fast WENO)格式,简称为WENO-F 格式。但是,七阶以上的WENO-F格式的计算稳定性略显不足[27]。
传统的光滑因子在光滑区被设计成尽量接近零的小量,最近Wu 等[27-28]认识到如果减小光滑区中候选模板的光滑因子之间的差异,不必满足光滑因子尽量接近零的条件,就能够减小WENO 格式的非线性权和线性权之间的差异。为了实现这一目标,Wu等[27-28]构造了一类光滑因子,使得各个候选模板上的光滑因子对于正弦函数为同一常数。基于该光滑因子通过WENO-Z 型非线性权得到了满足七阶直至十七阶精度的WENO 格式[27,28],简称为WENO-S 格式。然而,由于算子函数定义的限制,WENO-S 格式至少为七阶,不能得到在实际应用中需求更广泛的五阶及以下的WENO 格式。
对于WENO 格式,构造新的光滑因子至少需要满足以下两点要求:1)WENO 格式在光滑区域满足精度条件[18-19];2)在间断区保持本质无振荡的计算稳定性。
为了满足上述光滑因子的设计要求,本文基于WENO-S 格式光滑因子对于特定函数为常数的准则,设计了一种适用于五阶WENO 格式的新型光滑因子。数值实验表明新型WENO 格式不仅能够准确地捕捉强激波,而且能够模拟剪切层和声波等精细流场结构。
1 控制方程与数值方法
1.1 控制方程
本文的数值方法主要应用于Euler 方程和Navier-Stokes 方程。以二维可压缩守恒变量形式的无量纲Navier-Stokes 方程为例进行说明。
其中守恒变量为:
x、y方向的通量分别为:
其中总能为:
粘性应力项为:
传热项为:
其中,Re和Ma分别为参考雷诺数和参考马赫数,Pr=0.72,比热比γ=1.4,黏性系数由Sutherland 公式计算:
其中Tref为参考温度。
无量纲形式的完全气体状态方程和声速方程分别为:
1.2 数值方法
本文研究的数值格式主要用于离散Euler 或者Navier-Stokes 方程的对流项,下面以x方向的离散为例进行说明。
WENO 格式采用如下公式来离散导数项:
其中通过WENO 重构的方法来计算。对于系统方程,例如Euler 或者Navier-Stokes 方程,需要先把物理通量F投影到特征空间,然后对每一维的特征变量进行标量形式的WENO 重构过程。计算出标量形式的数值通量之后,再通过逆特征投影得到物理空间中的数值通量。详细计算步骤可参考文献[9,13]。
WENO 格式的本质是对标量形式的特征变量进行计算,因此下文重点以标量形式来说明五阶WENO 格式的详细计算过程。
首先对通量f进行分裂f(u)=f+(u)+f−(u),满足迎风性条件:常用的Lax-Friedrichs 分 裂 为其 中
WENO 格式需要对和分别进行计算,然后组合成数值通量
1.2.1 线性子重构格式和线性权
在三个候选子模板S0={xj−2,···,x j}、S1={xj−1,···,xj+1}和S2={xj,···,xj+2}上的子重构分别为:
从而可以计算出线性权值为:d0=1/10,d1=6/10,d2=3/10。
本文中所有的五阶WENO 格式的子重构和线性权取值都是一致的,下文不再赘述。
1.2.2 WENO-JS 格式的光滑因子和非线性权
五阶WENO-JS 格式[14]在三个候选子模板上的光滑因子为具体为如下形式:
对其Taylor 展开,可得:
根据线性权和光滑因子可以计算出非线性权:
其中,ε用于防止分母为零,一般取值为ε=1×10−6。归一化后的非线性权为:
根据非线性权和三个子重构式(12)可以得到五阶WENO-JS 格式:
1.2.3 WENO-Z 格式的光滑因子和非线性权
WENO-Z 格式[19,20]在三个候选子模板上的光滑因子与WENO-JS 格式保持一致,而WENO-Z 格式的重要创新之处是引入了全局光滑因子τ5,它表征了总模板的光滑性,其中五阶全局光滑因子为
WENO-Z 格式的非线性权取为如下形式:
其中,ε用于防止分母为零,一般取值为ε=1×10−40。归一化后的非线性权为:
Borges 等[19]推导出WENO-Z 型非线性权满足五阶精度的充分条件为:
根据非线性权和三个子重构式(12)可以得到五阶WENO-Z 格式:
1.2.4 WENO-NS 格式的光滑因子和非线性权
五阶WENO-NS 格式[22]在三个候选子模板上的光滑因子取为如下形式:
其中参数取为ξ=0.4。
五阶全局光滑因子为:
对其Taylor 展开,可得:
WENO-NS 格式的非线性权取为如下形式:
其中,ε用于防止分母为零,一般取值为ε=1×10−40。归一化后的非线性权为:
根据非线性权和三个子重构式(12)可以得到五阶WENO-NS 格式:
1.2.5 WENO-F 格式的光滑因子和非线性权
五阶WENO-F 格式[26]在三个候选子模板上的光滑因子取为如下形式:
五阶全局光滑因子为:
对其Taylor 展开,可得:
WENO-F 格式的非线性权取为如下形式:
其中,ε用于防止分母为零,一般取值为ε=1×10−40。归一化后的非线性权为:
根据非线性权和三个子重构式(12)可以得到五阶WENO-F 格式:
1.3 新型光滑因子和非线性权
Wu 等[27,28]针对描述波动属性的基本函数f(x)=sin(x),得到其导数关系:对于r≥4, (f(r−2))2−f(r−3)f(r−1)=1。由此发展了一类适用于多尺度流动问题的七阶及以上WENO 格式的光滑因子。通过简单的导数运算,可以发现当r= 3 时, (f′)2−f f′′=1也是成立的。本文以此为基础,发展了五阶WENO 格式的光滑因子。
首先将导数关系推广到更一般的正弦函数f(x)=Asin(ωx+φ),经过简单的导数运算可以得到(f′)2−f f′′=A2ω2是常数。然后将导数关系推广到更一般的情形(f′)2−µf f′′=C,其中μ和C为常数。求解该微分方程可以得到对应的函数形式。
以下举例说明。对于微分方程(f′)2−f f′′=1,还可以得到另一个特解为f(x)=sinh(x)。对于微分方程(f′)2−2f f′′=0,可以得到一个特解为f(x)=x2。对于微分方程(f′)2−µf f′′=C2,其中μ和C为任意常数,可以得到一个特解为f(x)=Cx。对于微分方程(f′)2−µf f′′=0,其中μ= 0.025,可以得到一个特解为
因此,当实际计算遇到的函数为这些特解时,对于特定的参数μ和C,就能满足导数关系(f′)2−µf f′′=C。
定义如下的算子函数[27,28]:
其中h是网格宽度。
通过Taylor 展开,可得:
因此,可以给出如下的算子函数关系:
其中μ为参数。
根据光滑因子设计的原理:当模板位于光滑区域,则光滑因子应该尽量接近零;当模板位于间断区域,则光滑因子应该尽量接近无穷大。因此符合光滑因子的设计原理,本文基于该函数来设计一类新型光滑因子。
由于光滑因子必须为正数才能保证计算的稳定性,而上式并不能满足该要求。经过数值试验,如果直接取上式的绝对值作为光滑因子会导致计算严重不稳定。借鉴WENO-NS 和WENO-S 格式的设计经验,我们取如下函数作为光滑因子:
其中,参数μ越大则格式的数值耗散越大;参数μ过小则会由于耗散不足而导致计算激波出现不稳定。经过大量的数值试验,本文中取µ=0.025,该参数能符合WENO 格式对激波捕捉和模拟精细结构的需求。由这种新型光滑因子构造的WENO 格式简记为WENO-XS 格式。
类似于三点模板的光滑因子推导过程,可以得到五点模板的新型五阶全局光滑因子:
WENO-XS 格式的非线性权取为如下形式:
其中,ε用于防止分母为零,本文取值为ε=1×10−40。归一化后的非线性权为:
根据非线性权和三个子重构式(12)可以得到新型五阶WENO-XS 格式:
2 精度分析和验证
2.1 新型光滑因子和非线性权的精度分析
对新型光滑因子式(39)进行Taylor 展开,可以得到如下的精度估计:
通过对比分析发现,如果忽略常数系数,WENO-JS、 WENO-Z、 WENO-NS 和 WENO-F 格式的光滑因子的Taylor 展开主项都是而新型光滑因子的Taylor 展开主项为可见新型光滑因子对候选模板的光滑性判断多出一项
以下从光滑函数问题和包含间断的问题两方面来分别说明:
1)光滑函数问题。
取f(x)=sin(πx),其计算域为−1 ≤x≤1,计算网格取为N= 20,网格宽度为h= 0.1。
图1 给出了WENO5-XS 格式光滑因子的两个分量在计算域内的分布,从图中可以发现在光滑函数的极值附近迅速减小,在其余区域的值则显著大于分量基本保持常数,这是由于对于函数满足导数关系式为常数,使得其中C为常数。 采用这两个分量作为光滑因子,分别计算得到的非线性权记为其分布如图2 所示。对于光滑函数,非线性权偏离线性权(d1=0.6)严重,显然是不符合设计要求的。总的非线性权ω1与线性权比较接近,是满足光滑问题的高精度计算需求的。
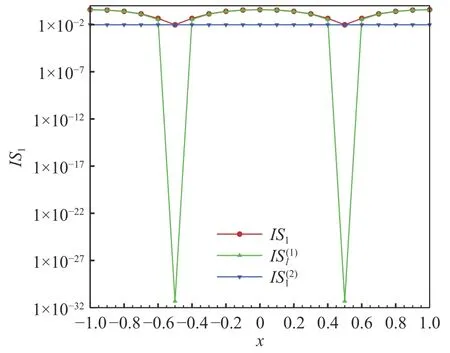
图1 对光滑函数WENO5-XS 格式光滑因子的两个分量Fig. 1 Smoothness indicator and its components of WENO5-XS scheme in smooth region
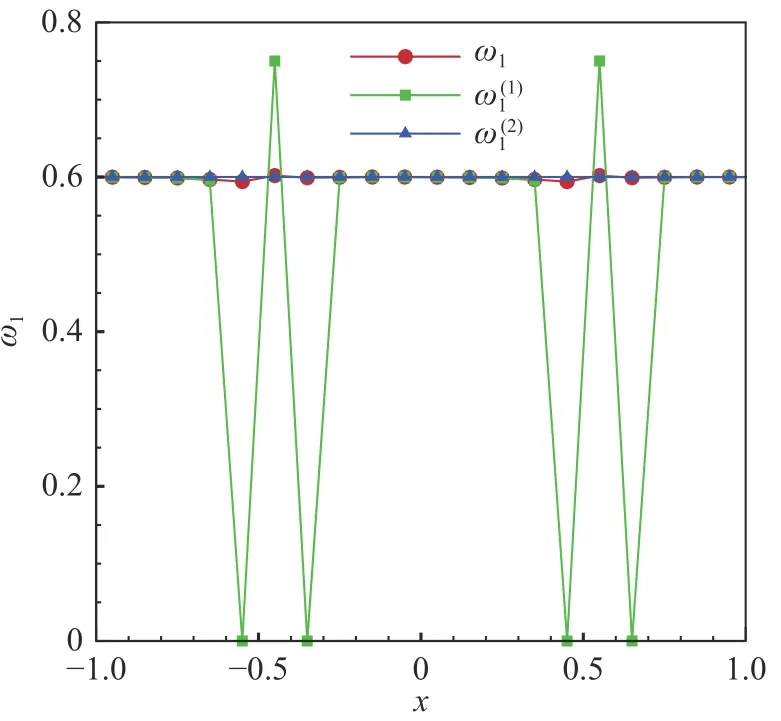
图2 对光滑函数WENO5-XS 格式光滑因子的两个分量计算的非线性权Fig. 2 Nonlinear weights of WENO5-XS scheme in smooth region
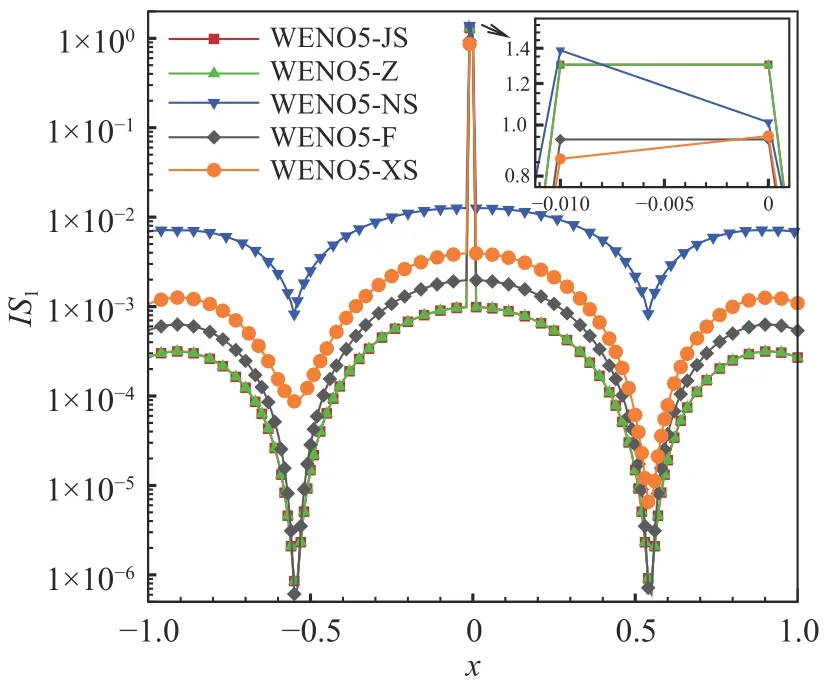
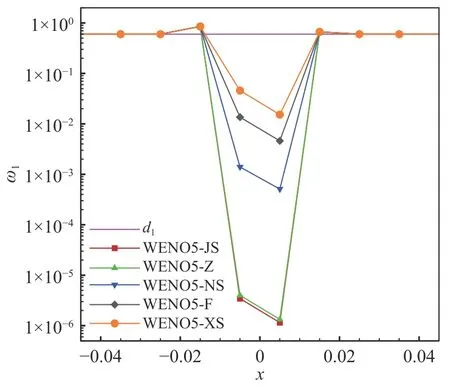
不同五阶WENO 格式的光滑因子和非线性权的比较如图3、图4 所示,可以发现WENO5-JS 格式的非线性权ω1与线性权d1的偏离较大,其余格式非线性权与线性权的差异较小。
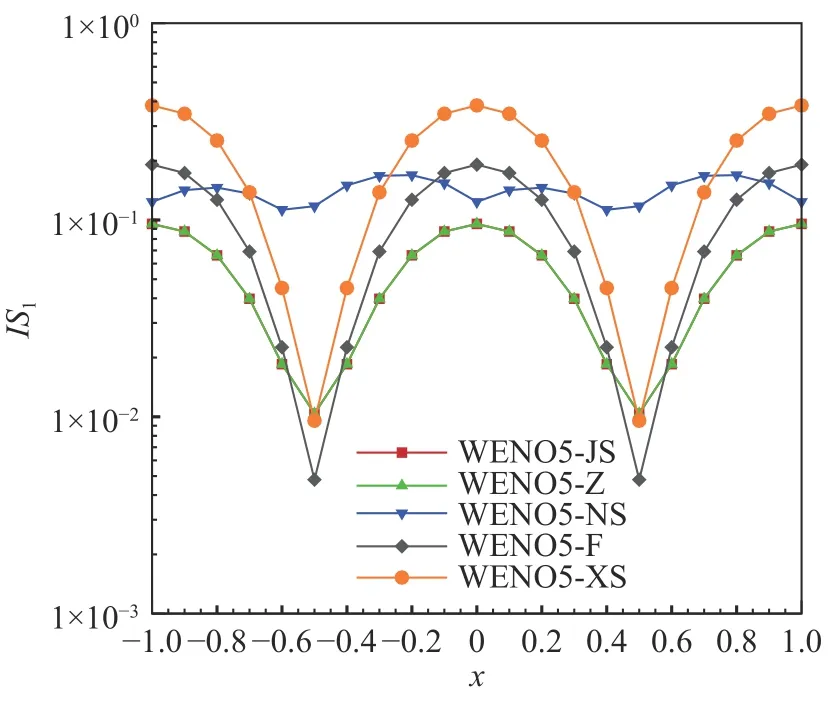
图3 对光滑函数不同五阶WENO 格式的光滑因子比较Fig. 3 Smoothness indicators of different WENO5 schemes in smooth region
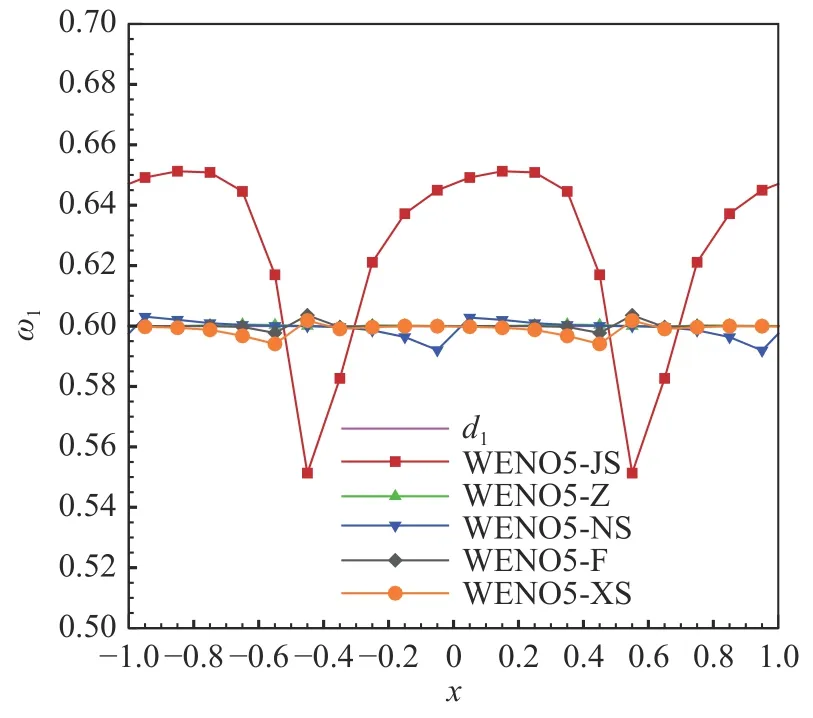
图4 对光滑函数不同五阶WENO 格式的非线性权比较Fig. 4 Nonlinear weights of different WENO5 schemes in smooth region
2)包含间断的问题。
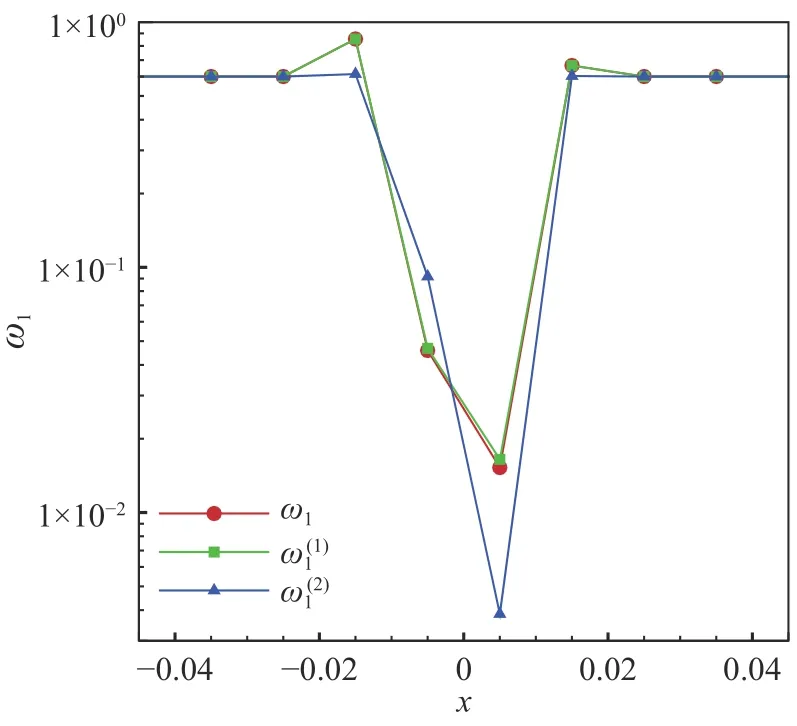
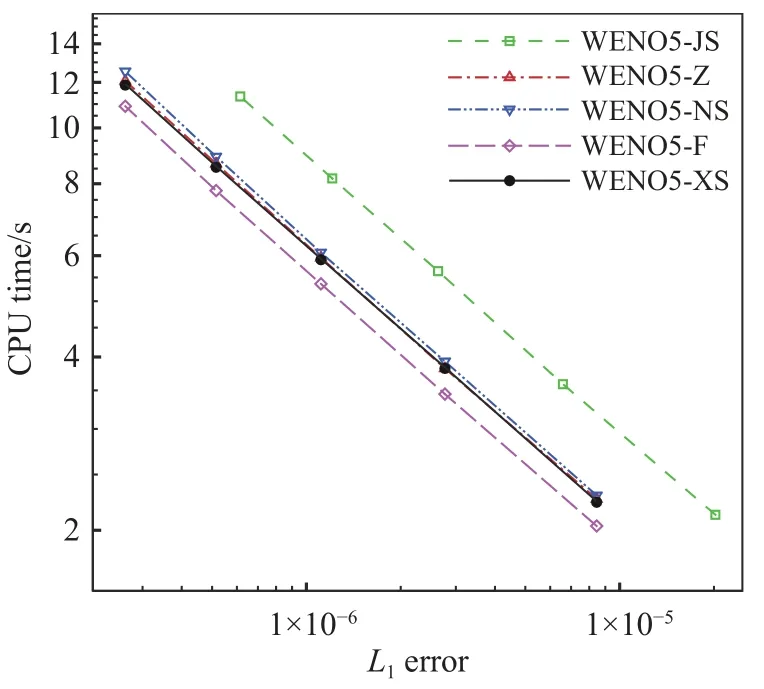
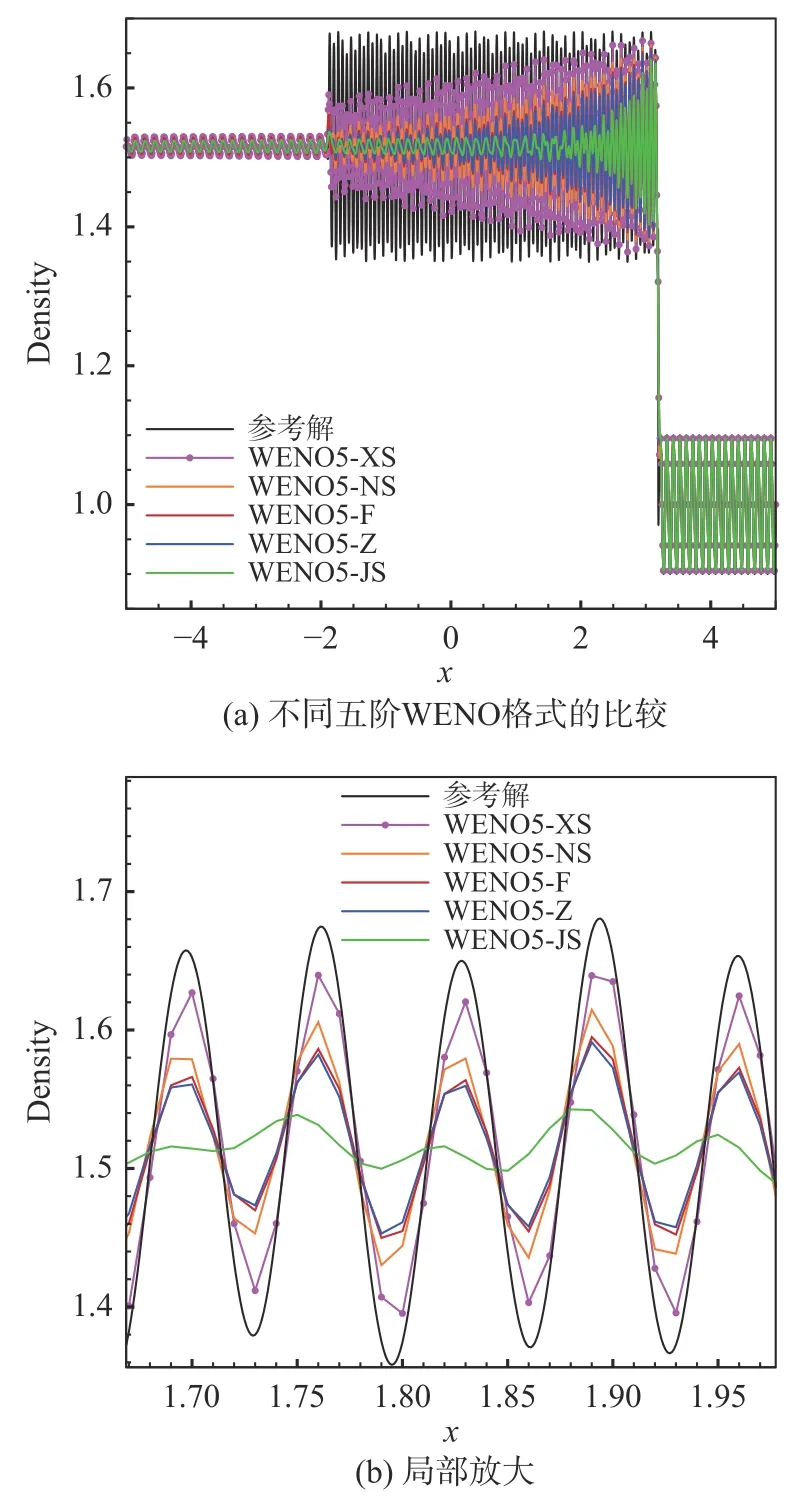
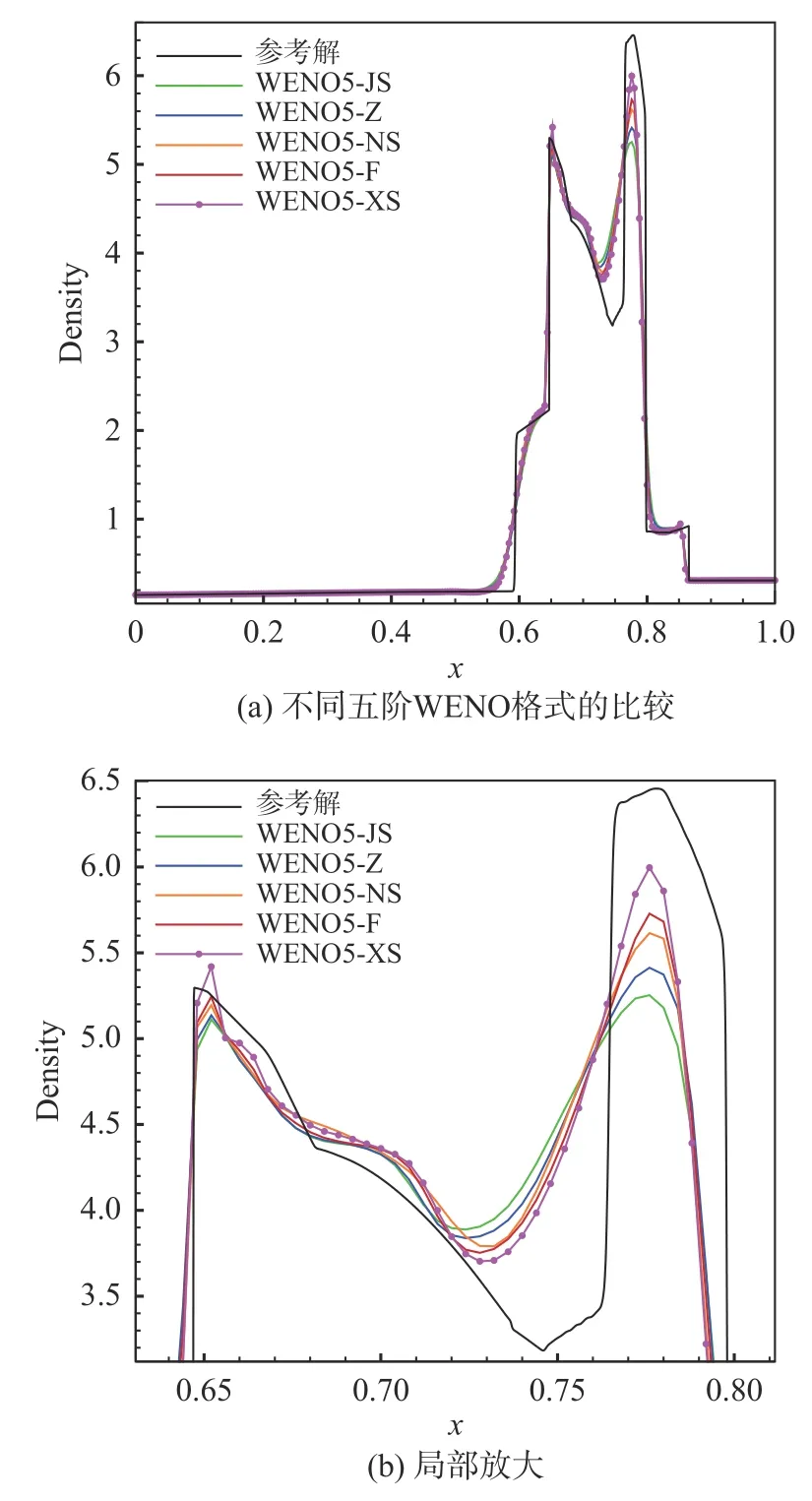
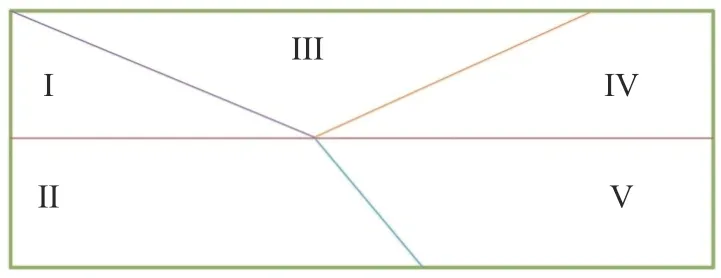
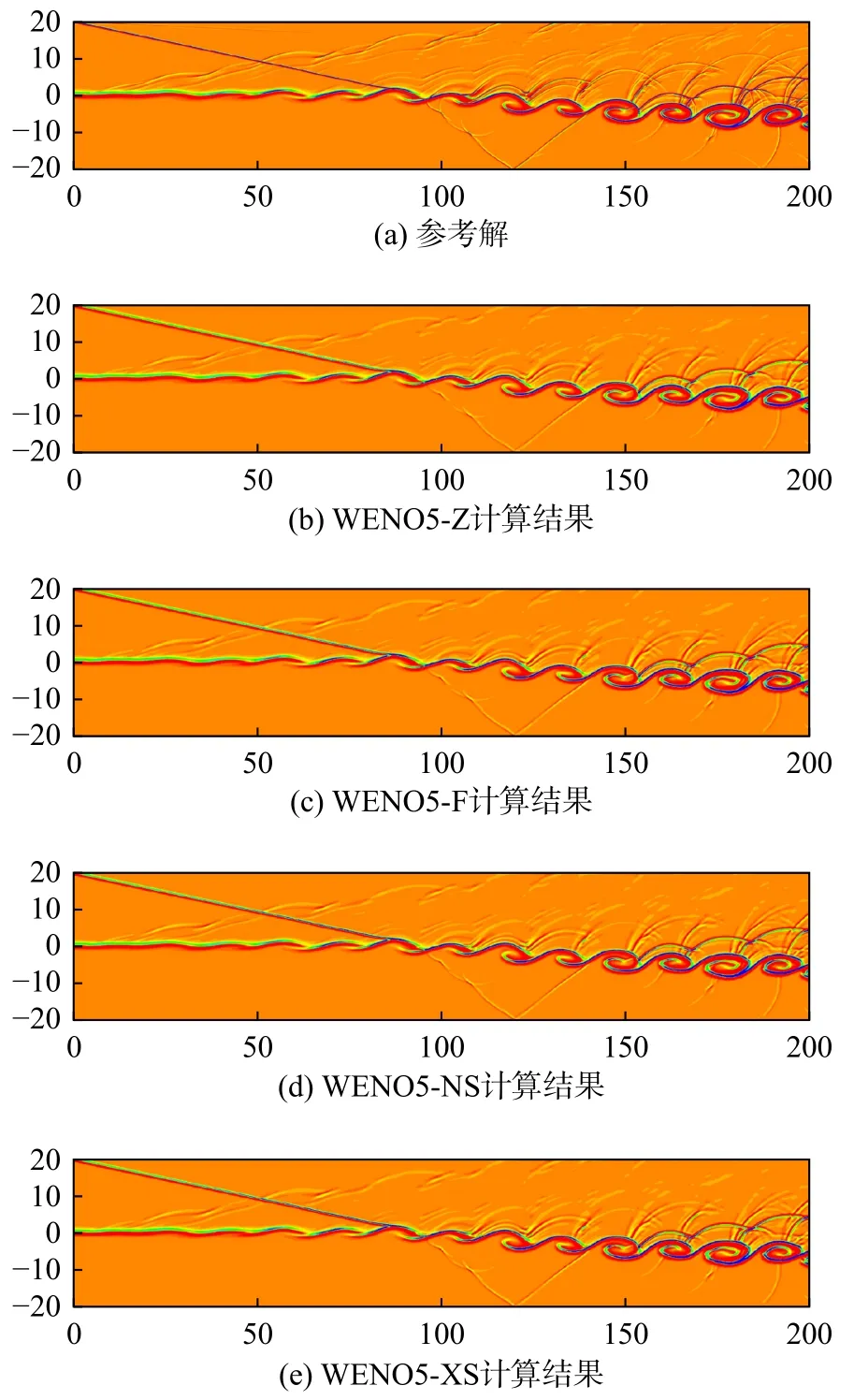
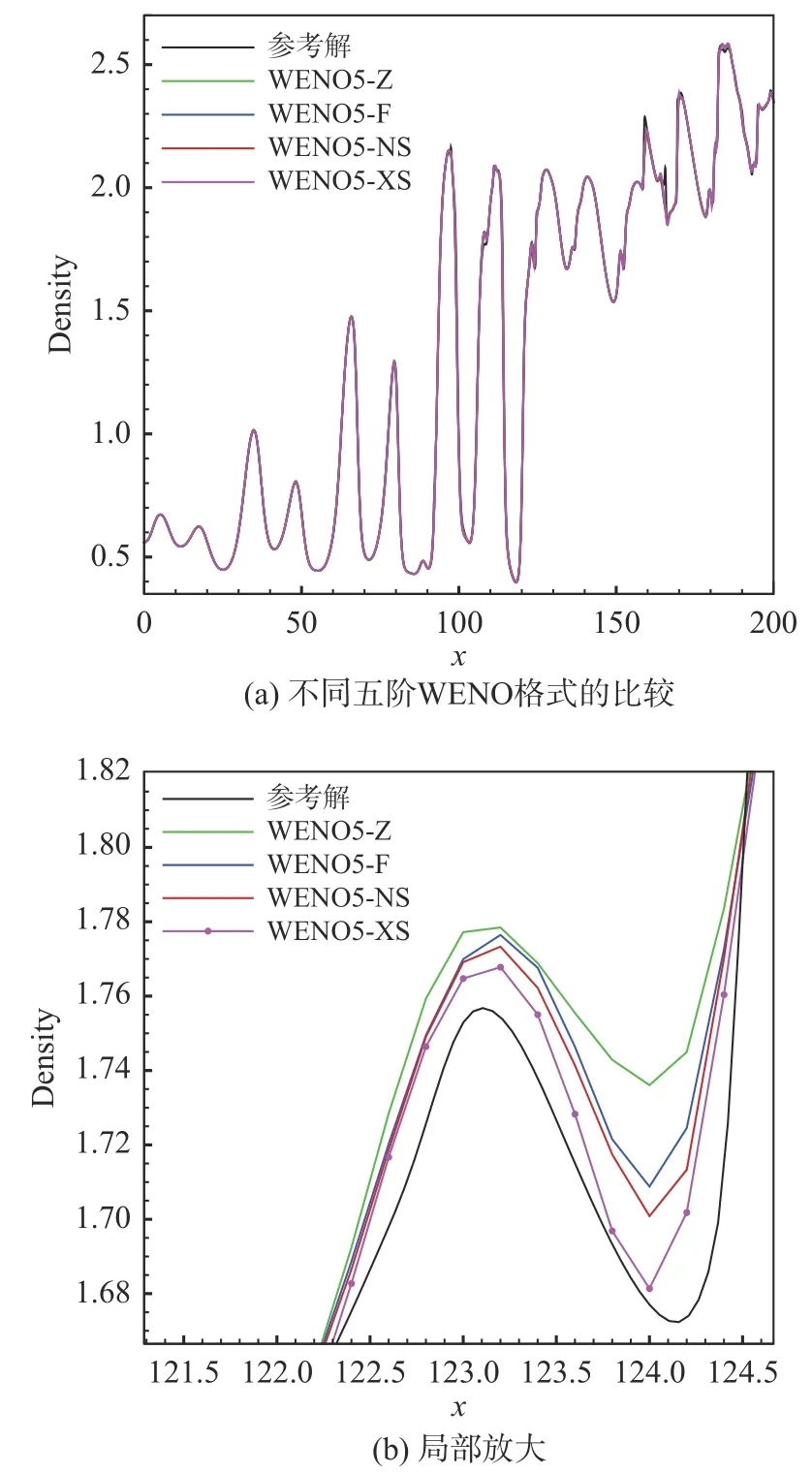
间断函数取为如下形式: 当−1 图5 给出了WENO5-XS 格式光滑因子的两个分量在计算域内的分布,从图中可以发现:对于光滑区域,IS1(1)在函数极值附近迅速减小,在其余光滑区域IS1(1)的值则显著大于IS1(2)。对于间断区域,IS1(1)和IS1(2)都能准确地识别间断点,并且IS1(1)的值比IS1(2)更大。采用IS1(1)和IS1(2)这两个分量作为光滑因子,分别计算得到非线性权记为ω1(1)和ω1(2),其分布如图6 所示。在间断处,非线性权ω1(2)的数值比ω(11)更小,说明IS1(2)对间断的识别起着重要作用,因此光滑因子两个分量之和IS1能更准确地识别间断。 图5 对间断函数WENO5-XS 格式光滑因子的两个分量Fig. 5 Smoothness indicator and its components of WENO5-XS scheme in discontinuous region 图6 对间断函数WENO5-XS 格式光滑因子的两个分量计算的非线性权Fig. 6 Nonlinear weights of WENO5-XS scheme in discontinuous region 不同五阶WENO 格式的光滑因子和非线性权的比较如图7、图8 所示,可以发现间断点处WENO5-JS 格式的非线性权值ω1相对较小,对间断的抹平最严重;在间断点处WENO5-XS 格式的非线性权值ω1相对较大,对间断的分辨率更好。 图7 对间断函数不同五阶WENO 格式的光滑因子比较Fig. 7 Smoothness indicators of different WENO5 schemes in discontinuous region 图8 对间断函数不同五阶WENO 格式的非线性权比较Fig. 8 Nonlinear weights of different WENO5 schemes in discontinuous region 对新型五阶全局光滑因子进行Taylor 展开,可以得到: 把以上的精度估计代入非线性权,可以得到如下的关系: 归一化后的非线性权为: 当不存在临界点,即当fj′≠0时,式(47)满足五阶精度的充分条件式(20),此时WENO-XS 格式达到五阶最优精度要求。 当存在一阶临界点,即当fj′=0时, 同样的推导方法可以得到:ωXrS=dr+Oh4,因此仍然满足五阶精度的充分条件式(20)。 为了验证数值方法的精度,我们选取如下的格式:时间离散采用三阶TVD Runge-Kutta 格式[10],通量分裂采用Lax-Friedrichs 分裂,空间离散采用五阶WENO-XS 差分格式。 以一维Euler 方程的对流密度波问题为验证标准[29],其精确解为: 计算域取为[0,2],边界取为周期性边界条件。计算的最终时刻取为100 个周期t=200,初始的计算网格为80 个点,CFL = 0.5。随着网格点数增大,CFL 数取为其中下标“1”表示上一个时间层的值,下标“2”表示下一个时间层的值,N表示网格点数,n= 5 表示空间离散精度。计算得到的数值结果如表1 所示。该问题包含一阶临界点,数值结果验证了WENO-XS 格式在一阶临界点处也达到了五阶的设计精度。 表1 五阶WENO-XS 格式的数值精度验证Table 1 Numerical accuracy of WENO5-XS scheme 采用CPU 计算时间和L1平均误差作为综合因素来评价数值格式的计算效率。计算结果如图9 所示,可以发现计算效率从高到低依次是 WENO5-F、WENO5-XS、WENO5-Z、WENO5-NS 和WENO5-JS 格式。其中WENO5-F 格式的计算效率最高,主要得益于WENO5-F 的光滑因子的形式最简洁。WENO5-JS 格式计算效率最低,主要是由于在相同网格下其计算误差较大。WENO5-XS 格式的计算效率比较高,这是因为其光滑因子的形式比WENO5-JS 和WENO5-NS 的形式更简洁,并且WENO5-XS 格式的三个光滑因子在计算时只需平移一个坐标点,此优点更利于编程和数值计算。 图9 不同五阶WENO 格式计算效率的比较Fig. 9 The comparison of computational efficiency for different fifth-order WENO schemes 为了验证新型WENO-XS 格式在双曲守恒方程中的计算准确度和稳定性,本文计算了一维Euler 方程、二维Euler 方程和二维Navier-Stokes 方程。时间离散采用三阶TVD Runge-Kutta 格式[10],通量分裂采用Lax-Friedrichs 分裂,空间离散采用多种不同的五阶WENO 格式用于比较计算结果。 本问题的控制方程是一维Euler 方程。Titarev–Toro 问题[30]流场中含有丰富的密度波结构,能够考察计算格式对流场细节的分辨能力,是验证数值格式的标准算例。该问题的初始条件为: 计算区域取为[−5, 5],初始间断位于x=−4.5处,最终计算时刻取为t= 5。边界处采用初始边界值。采用10000 个网格点的五阶WENO-JS 格式的计算结果来作为参考解。 本问题分别采用五阶WENO-JS 格式、WENOZ 格式、 WENO-F 格式、 WENO-NS 格式和新型WENO-XS 格式来进行计算,密度波的分布如图10所示。为了便于比较,计算网格采用1000 个点,使得密度波的一个周期内有10 个点。由于高频的密度波区域是光滑区域,非常适合考察格式的短波分辨率和耗散性。从计算结果可以看出,新型WENO-XS 格式在本问题中的计算结果与参考解最为接近,这说明WENO-XS 格式在光滑区的非线性权更接近线性权,分辨率更高,耗散更小。WENO-NS 格式的计算结果次之, WENO-F 格式比WENO-Z 格式计算结果略好,而WENO-JS 格式在本问题中对高频密度波的分辨率结果相对较差。 图10 不同五阶WENO 格式求解Titarev-Toro 问题Fig. 10 Solutions of the Titarev-Toro problem obtained by different fifth-order WENO schemes 本问题的控制方程是一维Euler 方程。双冲击波问题[31]包括了强激波、接触间断和膨胀波之间的相互作用,对计算格式的稳定性要求比较高。其初值为: 计算域两端采用反射边界条件,计算终止时间为t= 0.038,采用10000 个网格点的五阶WENOJS 格式的计算结果来作为该问题的参考解。 本问题分别采用五阶WENO-JS 格式、WENOZ 格式、 WENO-F 格式、 WENO-NS 格式和新型WENO-XS 格式来进行计算,密度的分布如图11 所示。计算网格采用250 个点。本问题中由双冲击波形成的间断区域非常适合考察格式的激波捕捉特性。从计算结果可以看出,新型WENO-XS 格式在本问题中的计算结果与参考解最为接近, 对间断的识别较为准确。WENO-F 格式比WENO-NS 格式计算结果略好,WENO-Z 格式计算结果比WENO-JS 格式好。 图11 不同五阶WENO 格式求解双冲击波问题Fig. 11 Solutions of two interacting blast waves obtained bydifferent fifth-order WENO schemes 由于WENO-Z 格式、WENO-F 格式、WENO-NS格式和新型WENO-XS 格式采用的都是WENO-Z 类型的非线性权,对于高频波的分辨率和激波捕捉优于传统的WENO-JS 类型的非线性权。因此,对于二维问题,不再给出WENO-JS 格式的计算结果。 本问题的控制方程是二维Euler 方程。双马赫反射问题[31]包含强激波和滑移线,非常适合于考察格式的激波捕捉能力和流场精细结构的分辨率。本问题描述的是马赫数为10 的强运动斜激波以与x轴方向呈60°角的方向入射,入射点在(1/6,0),计算区域取[0,4] × [0,1]。激波波前静止空气的密度为1.4,压力为1,波后按激波关系给定初始条件。初始物理参数为: 下边界在[1/6,4]的区域给定壁面反射边界条件,其它边界按照激波运动所在的位置分别给定波前或波后的值。本文采用1500×375 的均匀网格计算到无量纲时间t= 0.2。 本问题分别采用五阶WENO-Z 格式、WENOF 格式、WENO-NS 格式和新型WENO-XS 格式来进行计算,结果如图12 所示,取密度为1.6~21 共30 条等值线作图。本问题比较不同格式主要关注马赫杆和滑移线附近的分辨率,因此为了更好地比较不同的计算结果,在图中仅给出涡卷起区域(blow-up region)。从计算结果可以看出,新型WENO-XS 格式得到的旋涡结构是最丰富的,对流场精细结构的分辨率最高, WENO-NS 格式比WENO-F 格式计算结果略好,WENO-Z 格式的计算结果相对较差。 图12 不同五阶WENO 格式求解双马赫反射问题Fig. 12 Solutions of the double Mach reflection problem obtained by different fifth-order WENO schemes 本问题的计算结果可以验证新型WENO-XS 格式不仅能够模拟滑移线等精细结构,同时能够准确地捕捉激波。 本问题的控制方程是二维Euler 方程。前台阶问题[31]的初始条件为马赫数为3 的强运动激波沿着带有台阶的风洞向右传播。台阶高度为0.2,前缘位置在0.6,计算域为[0,3] × [0,1]。初始物理参数为: 左、右边界为开边界,其余边界取壁面反射条件。本文采用720×240 的均匀网格,计算截止到无量纲时间t= 4 的时刻。 本问题分别采用五阶WENO-Z 格式、WENOF 格式、WENO-NS 格式和新型WENO-XS 格式来进行计算,结果如图13 所示,取密度为0.2568~6.607共60 条等值线作图。本问题比较不同格式主要关注滑移线附近的分辨率。从计算结果可以看出,新型WENO-XS 格式识别的旋涡结构是最丰富的,对流场精细结构的分辨率最高,WENO-NS 格式的计算结果次之,WENO-F 格式与WENO-Z 格式的计算结果相当。 图13 不同五阶WENO 格式求解前台阶问题Fig. 13 Flow fields around a forward facing step obtained by different fifth-order WENO schemes 本问题的计算结果可以验证新型WENO-XS 格式能够准确地捕捉强激波,同时能够分辨出滑移线附近更多的旋涡精细结构,说明WENO-XS 格式的耗散是相对最小的。 本问题的控制方程是二维可压缩Navier-Stokes方程。本问题是典型的激波噪声问题,在论文[32,33]中有详细的描述和分析。以下简要说明计算的初始条件和边界条件。整个剪切层在初始时刻是等压的,并且总的焓值也处处相等。计算域取为[0,200]×[−20,20]。初始时刻可以把计算域分成如图14 所示的5 个部分,表2 给出了各个区域具体的流动参数。 表2 初始时刻流场的物理参数Table 2 Parameters of the initial flow field 图14 初始流场计算域的划分Fig. 14 Decomposition of the computational domain at the initial state 网格在x方向取均匀网格,在y方向取拉伸网格,拉伸变换关系为y方向的计算域长度为Ly=40,拉伸因子by=1,计算网格η∈[−1,1]为均匀网格。 上边界条件取激波波后的值,即取Ⅲ区的值。下边界条件取为滑移壁面边界条件。出口处用远场特征边界条件。 本问题采用1000×200 的网格规模,计算截止到无量纲时间t= 120 的时刻。 采用3800×900 网格点的五阶WENO-JS 格式的计算结果作为该问题的参考解。本问题分别采用五阶WENO-Z 格式、WENO-F 格式、WENO-NS 格式和新型WENO-XS 格式来进行计算,结果如图15 所示,取密度阴影为−3.5~0.5 共30 条等值线作图。本问题比较不同格式主要关注剪切层和声波的分辨率。新型WENO-XS 格式对超声速剪切层外部的小激波结构识别相对较为清晰,对声波的分辨率相对较好。为了能够更清晰地显示不同格式之间的差别,取t= 120 时刻横向中心线位置(y= 0)的密度剖面进行比较(图16)。从密度剖面的计算结果可以看出,新型WENO-XS 格式在本问题中的表现是最好的,其计算结果与参考解最为接近, WENONS 格式的计算结果比WENO-F 格式略好, WENOZ 格式的计算结果相对较差。 图15 不同五阶WENO 格式求解激波剪切层相互作用问题Fig. 15 The interaction of shock wave and shear layer obtained by different fifth-order WENO schemes 图16 不同五阶WENO 格式沿y = 0 的密度分布Fig. 16 The distribution of density along y = 0 obtained by different fifth-order WENO schemes 计算结果可以验证新型WENO-XS 格式不仅能精细模拟剪切层和声波,同时能准确捕捉强激波。 本文针对广泛应用的五阶WENO 格式,采用算子函数近似导数关系的方法,设计了一种新型光滑因子。在间断区域,与传统的光滑因子相比,新型光滑因子对模板的光滑性判断更好,对间断的识别更准确。在光滑区域,新型光滑因子使得新型WENO 格式的非线性权更接近线性权。 理论分析和数值验证表明新型WENO 格式具有五阶精度,即使在一阶临界点也能保持一致五阶精度。 对于一维激波管问题,通过与WENO-JS、WENOZ、WENO-F 和WENO-NS 格式的比较,从计算结果可以发现新型WENO-XS 格式与参考解最为接近,对短波的分辨率最高,格式的耗散性最小,同时对激波的间断识别最准确,具有良好的激波捕捉特性。 对于二维包含激波的流动问题,通过与其他WENO 格式的比较,计算结果表明新型WENO-XS 格式不仅能够准确地捕捉强激波,而且能够模拟剪切层和声波等精细流场结构,得到的旋涡结构是最丰富的,对旋涡和声波的分辨率最高。 本文提出的五阶WENO-XS 格式在求解包含激波的复杂流动问题中具有潜在的应用价值。提出的新型光滑因子构造思路不局限于五阶,可以推广到更高阶的WENO 格式,相关的工作还需进一步研究探索。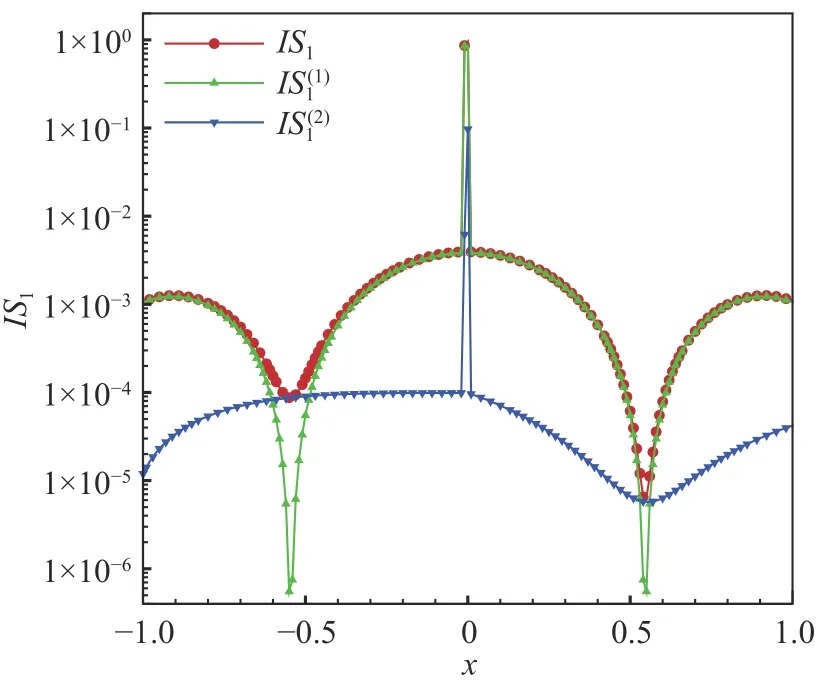
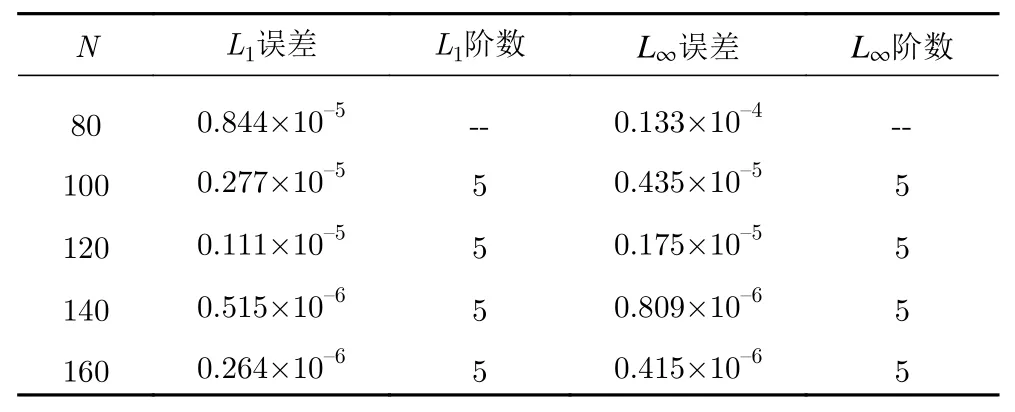
2.2 数值精度验证和计算效率
3 数值实验与分析
3.1 Titarev–Toro 问题
3.2 双冲击波问题
3.3 激波双马赫反射问题
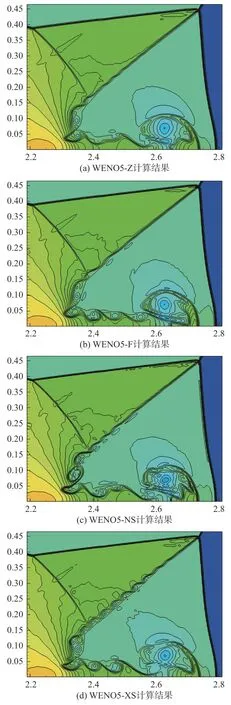
3.4 前台阶问题
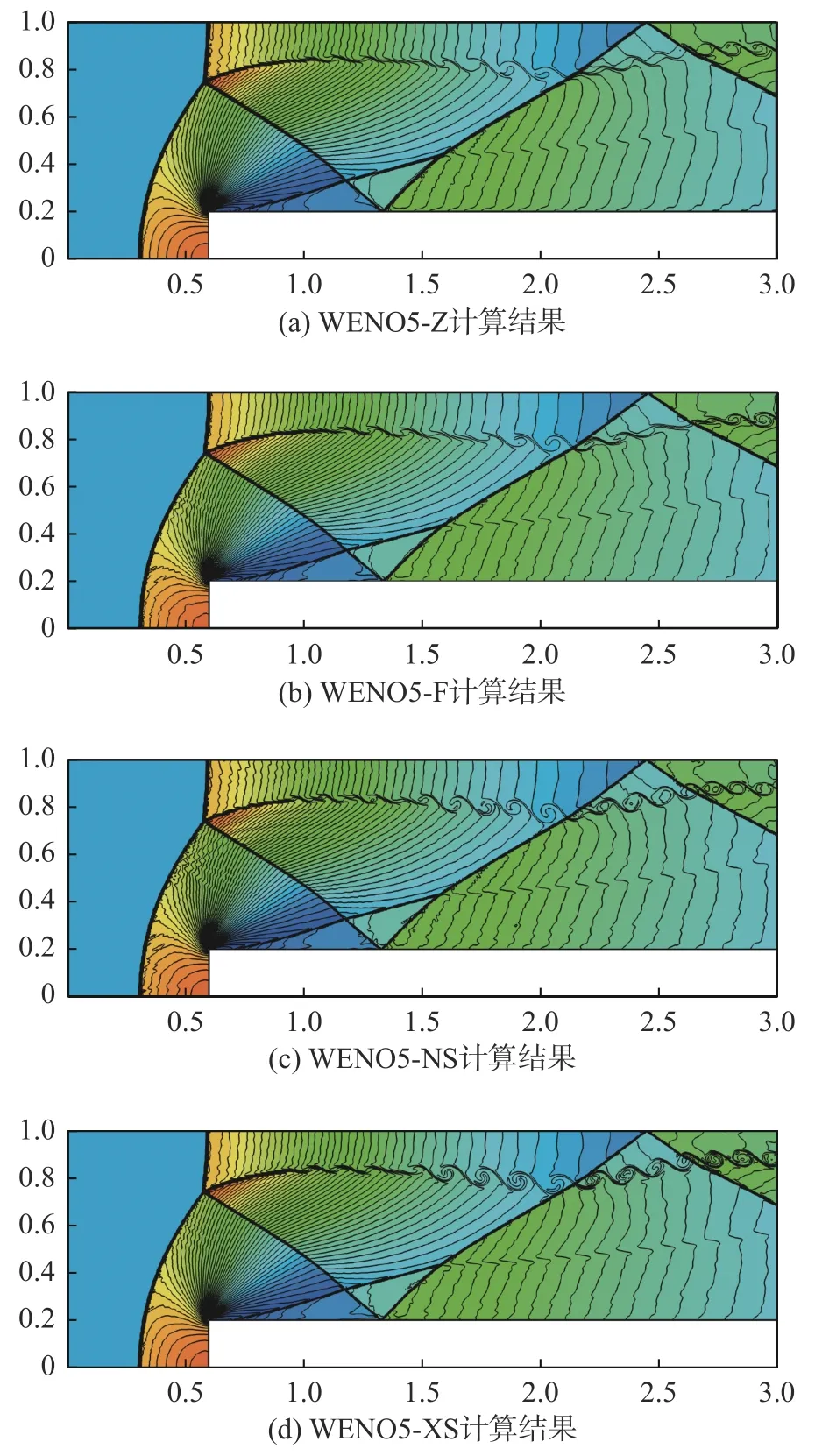
3.5 激波与剪切层相互作用
4 结 论

