基于DFT-SAMP算法的MIMO-VLC系统压缩感知信道估计
张峰,凌锦炜,刘叶楠,赵黎
(西安工业大学 电子信息工程学院, 西安 710021)
0 引言
VLC 是一种利用可见光波段作为通信载体,兼顾照明和数据传输的新型通信方式,具有无电磁干扰、频谱资源丰富等优点[1-3]。将MIMO 与VLC 系统结合,可以有效实现空间资源的复用,提高系统通信容量和速率[4-5]。但是MIMO-VLC 系统需要准确的信道估计来获取信道状态信息保证通信的可靠性。
信道估计常用的最小二乘(Least Squares,LS)算法,虽然复杂度低,但需要大量导频开销,导致频谱利用率降低[6-7],同时LS 算法估计的信道状态信息存在较大误差,导致系统整体可靠性不足。由于压缩感知(Compressed Sensing,CS)可实现低于奈奎斯特速率的方式采样信号,且具有较高的重构精度,因此被应用于信道估计当中,可利用少量的导频开销获取良好的信道估计性能[8-10]。文献[11]在MIMO-VLC 系统的信道估计中引入了正交匹配追踪(Orthogonal Match Pursuit,OMP)算法,证明了CS 算法在VLC 系统信道估计中的可行性,但需要预知信道的真实稀疏度,而信道的真实稀疏度通常是无法准确预知的,故在实际运用中存在局限性。文献[12]在MIMO-OFDM 系统中通过SAMP 算法在信道稀疏度未知情况下,自适应重构出信道特性,解决了OMP 算法需预知信道稀疏度的问题,但也增加了算法迭代次数,降低了效率。文献[13]提出了一种正则化稀疏度变步长自适应匹配追踪 (Regularized Sparsity Variable Step-size Adaptive Matching Pursuit, RSVssAMP)算法,在SAMP 算法的基础上加入了变步长的思想,通过大步长减少迭代次数,但存在过估计问题,算法稳定性降低。文献[14]提出一种基于有限等距性质(Restricted Isometry Property,RIP)的稀疏度预测自适应匹配追踪(RIP Based Prediction-sparsity Adaptive Matching Pursuit,RSAMP)算法,通过基于RIP 的稀疏度预测方法快速迭代完成信道估计,但其稀疏度预测的方法复杂度较高,不利于系统效率的提升。
为了以更高效的方式保证MIMO-VLC 系统通信的可靠性,本文提出一种DFT-SAMP 信道估计算法。通过基于DFT 的稀疏度预测方法,对信道稀疏度进行预估计,将估计出的稀疏度作为SAMP 算法初始步长,使其快速逼近信道的真实稀疏度,提高运行速率。
1 MIMO-VLC 信道特征及增益模型
MIMO-VLC 系统中有Nt个LED 光源和Nr个光电探测器PD,每个LED 光源发送的光信号可经过直射链路(Line of Sight,LOS)和非直射链路(No Line of Sight,NLOS)到达接收端,具体通信场景如图1。
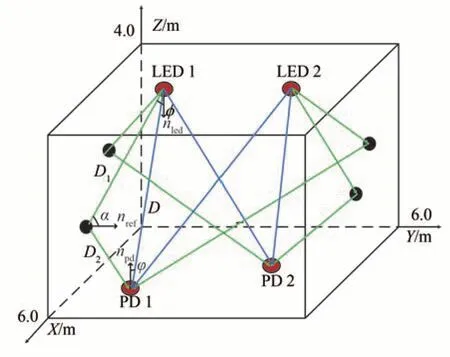
图1 MIMO-VLC 通信几何场景Fig.1 MIMO-VLC communication geometric scenario
LED 光源与光电探测器PD 间信道特征可由冲激响应h(t)表示为
式中,Rnt为发射端特征,Rnr为接收端特征;g为光反射次数,g=0 时,光信号经LOS 信道直射到达接收端;g=1 时,光信号经过NLOS 信道到达接收端。光信号经LOS 信道时的冲激响应[15]为
式中,Ar为光电探测器接收面积;φ为光入射角;D=|Rnt-Rnr|为发送端与接收端间的距离;c为光速。T(ϕ)为光源辐射强度,常用由式(3)表示的朗伯模型:
式中,m为朗伯模式指数;ϕ为光源出射角。光信号经过NLOS 信道时,冲激响应为
式中,in为反射单元个数,ΔA为反射单元面积;D1表示从光源到反射面的距离;D2为从反射面到接收端距离;α为光反射角。设采样间隔为T,则第nt个LED 到第nr个PD 间的多径信道增益[16]表示为
式中,τ0=D/c为LOS 信道PD 接收光信号时延;Lnt·nr-1 为路径数。设房间大小为6 m×6 m×4 m,取m=1,光电探测器接收面积Ar=1 cm2,反射单元面积ΔA=0.01 m2,采样间隔为T=5 ns,当LED 和PD中心坐标分别为(3,4.5,5)和(5,1.5,0)时,对应多径信道增益如图2。
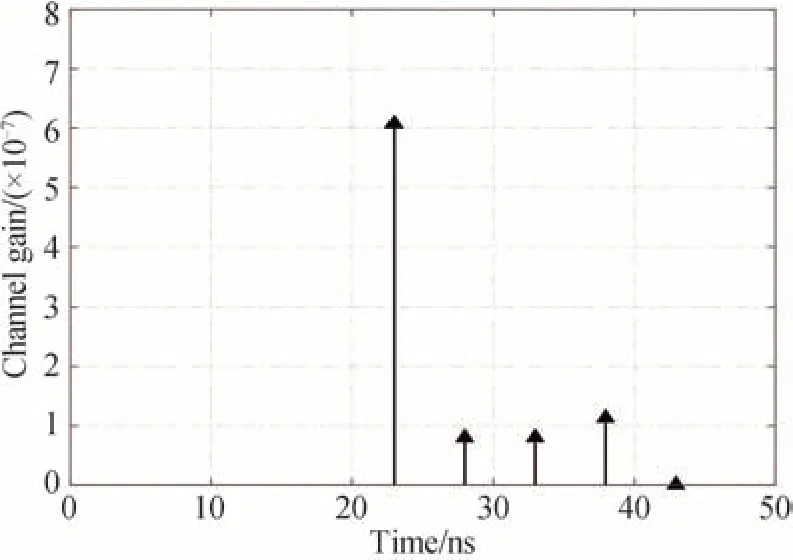
图2 多径信道增益Fig.2 Multipath channel gain
图中第一个路径的信道增益为LOS 信道的增益,且其值最大,而其余信道路径为光源经墙面反射到达PD 的信道增益,相对于较小。由于信道增益的符号长度与FFT 点数相同,均为256 点,而图2 中信道增益仅有5 个非零路径,具有明显稀疏性,因而MIMO-VLC 系统可以借助压缩感知的方式进行信道状态估计。
2 MIMO-VLC 系统及信道估计模型建立
2.1 MIMO-VLC 系统建模
在MIMO-VLC 系统中,数据信号经过正交振幅调制(Quadrature Amplitude Modulation,QAM)调制后进行空时块编码(Space Time Block Code,STBC),然后经过串并转换分为多个支路,每个支路分别进行正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)调制,最后经过直流偏置和D/A 转换后,由每个发送端的LED 发送信号,接收端的处理与发送端相对应,具体模型如图3。
设Nt个发送端的传输数据为X=[X0,X2,…,XNt-1],则接收数据Yj为
式中,Xi=diag{Xi(0),Xi(1),Xi(2),…Xi(N-1)}是N×N维方阵,hi·j为N×1 维信道冲激响应矩阵,Zj为N×1 维噪声向量,F为N×N维傅里叶变换矩阵,表示为
2.2 MIMO-VLC 信道估计模型
设发送端数据信号中插入导频符号数为P,选择矩阵为C,则接收导频符号YjP为
式中,XiP=CXiCT为P×P维导频信号;FP=CF 是P×N维对导频进行傅里叶变换的矩阵;ZjP=CZj为导频所受的噪声干扰。令,则式(8)可写为
忽略噪声影响,则通过式(9)可将MIMO-VLC 系统信道估计问题建模为压缩感知求解问题。
2.3 导频结构
采用非均匀梳状导频结构对MIMO-VLC 系统进行信道估计,具体结构如图4。

图4 导频结构示意Fig.4 Pilot structure diagram
图中,实心点表示导频信息,空白部分则为数据信息。每列代表一个OFDM 符号,每个OFDM 符号中导频位置相同,但由于接收端需要随机傅里叶矩阵作为压缩感知的观测矩阵,因此具体的导频位置采用随机选取的P个子载波位置。导频位置Dn由线性同余法获得,可表示为
式中,a为乘子,c为增量,均为正整数。选取不同a,c和初始值D0可递推获得随机导频位置,而接收端对导频进行傅里叶变换的矩阵即为部分随机傅里叶变换矩阵,构成压缩感知的观测矩阵。
3 基于DFT-SAMP 的压缩感知信道估计算法
3.1 压缩感知信道估计原理
设有N×1 维的信号B,表示为
式中,Ψ为N×N维正交基,Θ为N×1 维稀疏信号。若信号B可通过观测矩阵Φ压缩成M×1 维观测向量y,则y可表示为
式中,Φ为M×N维观测矩阵。若存在δk∈(0 , 1)使得观测矩阵Φ满足
则称观测矩阵Φ满足RIP 性质,观测向量y可通过重构算法精确重构信号B。而在MIMO-VLC 信道估计中,可将式(9)中的A作为压缩感知的观测矩阵Φ,YjP作为观测向量y,接收端即可通过压缩感知重构算法重构出信道冲激响应h。
3.2 基于SAMP 的信道估计算法
SAMP 算法通过确定稀疏度步长增量s,即可自适应迭代逼近重构目标,且引入回溯策略,将候选集中错误原子剔除以提高算法重构精度。具体步骤如下:
1)输入观测向量y=YjP,观测矩阵Φ=A,步长增量s。
2)初始化残差r0=y,步长Q=s,支撑集F0=∅。
3)从u=|ATrn-1|中选出内积值最大的前Q个原子,将原子位置索引Tn-1加入候选集Cn=(Tn-1∪Fn-1)。
4)计算x=(ΦTCnΦCn)ΦTCn y,选出|x|中最大的Q个原子,将原子位置索引存入支撑集Fn,并更新残差rFn=y-ΦFn(ΦTFnΦFn)ΦTFn y。
5)若‖rFn‖2≤ε,则进入步骤7)。
6)若‖rFn‖2≥‖rFn-1‖2,更新步长Q=Q+s;否则rn=rFn,Tn=Fn,返回步骤3)继续迭代。
7)输出信道冲激响应=(ΦTFnΦFn)ΦTFn y。
综上可知,步骤4)每次迭代将从候选集Cn中重新选取最匹配的Q个原子作为支撑集Fn,可以有效剔除上次迭代选取的错误原子。算法步长Q可通过步长增量s逐步递增达到真实稀疏度,而步长增量s的选择对算法性能有重要关系;若s取值小,则算法需多次迭代达到真实稀疏度,重构速率慢;若s取值大,则可能使算法的预测稀疏度存在过估计问题,导致重构精度降低。为获得较高的重构精度,通常采用小步长增量,因而算法需多次迭代才能完成信道估计,增加了运行时间。
3.3 基于DFT 的SAMP 信道估计算法效率优化
3.3.1 DFT 信道估计算法
DFT 算法在LS 算法基础上加入时域去噪处理,提高了估计性能,原理如下:
1)通过LS 算法估计导频位置处的信道特性频率响应
2)对进行N点IDFT 变换,得到信道冲激响应(n)
3)假设循环前缀长度为L,DFT 信道估计算法的去噪处理就是将估计的信道冲激响应(n)在L点之外的部分视为噪声,并置零,即
通步骤3)消除了(n)中的大量噪声干扰,降低了噪声对后续稀疏度预测的影响。
3.3.2 基于DFT 的稀疏度预测方法
采用求噪声阈值筛选初始候选集的方法,通过DFT 算法估计的冲激响应(n)获取能量阈值,进而筛选出能量较大的信道非零抽头,其对应的位置索引集合作为SAMP 算法的初始候选集,集合大小作为初始步长。具体步骤如下:
1)求(n)的平均能量e
2)通过加权系数λ确定阈值b
3)将能量大于阈值的位置索引作为初始化候选集Ω,其大小为先验稀疏度pre_k
3.3.3 DFT-SAMP 信道估计算法
通过基于DFT 的稀疏度预测方法对信道的稀疏度进行预估计,将预测的稀疏度作为SAMP 算法的初始步长,使算法步长从稀疏度预测值逐步递增达到真实信道稀疏度,减少算法迭代次数,提高算法运行速率。DFT-SAMP 算法具体实现步骤如下:
1)输入观测值y=YjP,观测矩阵Φ=A,步长增量s,初始候选集Ω,先验稀疏度pre_k。
2)初始化支撑集F0=Ω,步长Q=pre_k,残差r0=y-ΦCn(ΦTCnΦCn)ΦTCn y。
3)从u=|ATrn-1|中选出内积值最大的前Q个原子,将原子位置索引Tn-1加入候选集Cn=(Tn-1∪Fn-1)。
4)计算x=(ΦTCnΦCn)ΦTCn y,选出|x|中最大的Q个原子,将原子位置索引存入支撑集Fn,并更新残差rFn=y-ΦFn(ΦTFnΦFn)ΦTFn y。
5)若‖rFn‖2≤ε,则进入步骤7)。
6)若‖rFn‖2≥‖rFn-1‖2,更新步长Q=Q+s;否则rn=rFn,Tn=Fn,返回步骤3)继续迭代。
7)输出信道冲激响应=(ΦTFnΦFn)ΦTFn y。
4 实验与数据分析
4.1 实验平台及参数设置
基于实际室内环境进行MIMO-VLC 系统信道估计实验,实验系统结构如图5。
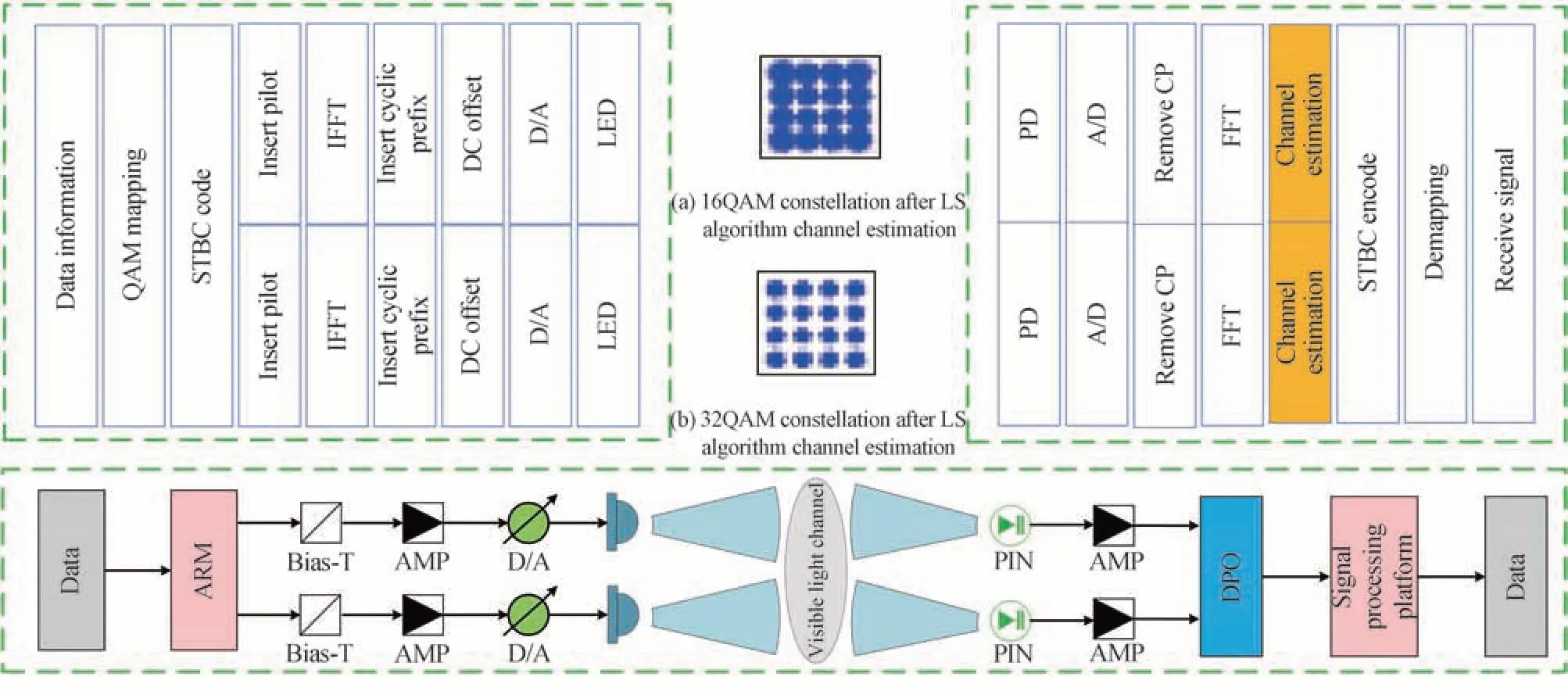
图5 实验系统结构图Fig.5 Experimental system structure
图中,发送端数据在ARM 处理器中进行调制后,输出的调制信号将依次经放大器(AMP-OPA657),直流偏置,最后通过LED 进行光信号传输;接收端,通过PIN 进行光信号转换,将接收信号发送到数字示波器(Tektronix 7354C)进行采集,最后将采集的信号发送到信号处理平台进行信号解调获得接收端数据。接收端经过LS 算法和所提算法信道估计的信号QAM 星座图如图5(a)和5(b)。图5(b)中的QAM 星座图比图5(a)的QAM 星座图更集中,定性地验证了所提算法信道估计性能优于LS 算法。实验场景为6 m×6 m×4 m 的LED 室内照明环境,压缩感知算法的精度实验参数如表1。

表1 系统仿真参数Table 1 System simulation parameters
4.2 算法的稀疏度预测可行性验证
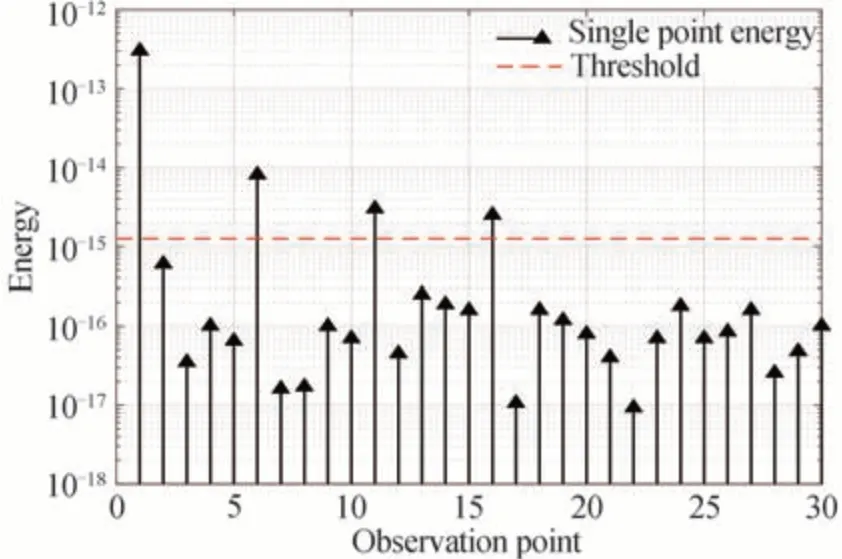
图6 能量与门限阈值分布情况Fig.6 Energy and threshold distribution
由图6 可知, DFT-SAMP 算法共筛选出4 个大于门限阈值的原子,故此时的初始步长为4,与真实信道稀疏度相差较小,可快速迭代完成信道估计,减少大量运行时间。此外尽管可能会选入少数错误原子,也可通过DFT-SAMP 算法的回溯策略去除。在同等条件下,将本次实验重复进行1 000 次得出的平均先验稀疏度为4.135,与真实信道稀疏度相差较小,表明基于DFT 的稀疏度预测方法的有效性。
4.3 算法稀疏度预测方法验证
通过对比真实信道频率响应H(k)与信道估计获得的频率响应之间的均方差分析算法信道估计性能,均方差定义为
均方差值越小,算法估计的信道特性越接近真实信道环境,估计性能越好。均方差曲线如图7。
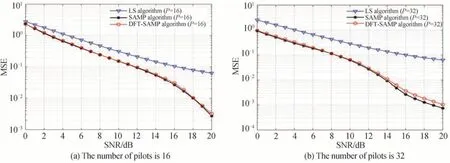
图7 算法的MSE 性能分析Fig.7 MSE performance analysis of the algorithm
图7 中的均方差性能曲线对比的是在16 个导频和32 个导频情况下,所提算法和LS 算法的信道估计均方差性能,由图7 可以看出,论文算法的MSE 性能明显优于LS 算法,且随着导频数的增加,性能增益更加明显。对于本文所提算法,利用DFT 稀疏度预测方法对信道稀疏度进行预测,实际的MSE 性能相较于SAMP算法略有下降,但并不明显。
4.4 算法可靠性分析
图8 是在调制阶数M=16 时,不同算法的误码率性能曲线。

图8 算法的BER 性能分析Fig.8 BER performance analysis of the algorithm
由图可知,在16 个导频情况下, 所提算法相较于LS 算法在满足前向纠错 (Forward Error Correction,FEC)误码率阈值(3.8×10−3)时的信噪比降低了2 dB;在32 个导频情况下,所提算法低于LS 算法4.5 dB,使误码率达到FEC 误码率阈值。所提算法在导频数为16 时的误码率性能就优于LS 算法导频数为32 时的误码率性能,如果使用论文算法代替LS 算法进行信道估计可减少50%的导频开销。同时DFT-SAMP 算法误码率性能与SAMP 算法误码率性能整体相当,说明基于DFT 的稀疏度预测方法在提高系统效率的同时,不会降低系统通信的可靠性。
图9 是4 种调制阶数情况下,导频个数P=32 时,算法的误码率性能曲线。

图9 不同调制阶数的BER 性能Fig.9 BER performance of different modulation orders
由图中可以看出,系统误码率随着调制阶数M的增大而增加,而本文算法相对于LS 算法的性能增益随着调制阶数的增大也更明显。在误码率达到FEC 阈值情况下,调制阶数M=8 时,本文算法相对于LS 算法性能有3.5 dB 提升,调制阶数M=16 时,性能则提升了4 dB,调制阶数M=32 时,性能提升6 dB,而调制阶数M=64 时,性能则有10 dB 的提升,该结果表明本文算法在调制阶数较高时对误码率的减低更为明显,有利于系统通信效率的提升。
4.5 算法效率分析
图10 是不同算法和导频数P的情况下,运行1 000 次的平均时间。

图10 算法平均运行时间Fig.10 Average running time of algorithm
从图中可以看出,LS 信道估计算法相对于CS 算法具有较短的运行时间,但通过图7 和图8 可知,LS 信道估计算法虽然运行速率较快,但整体信道估计性能相对差于CS 算法。对于CS 算法,基于DFT 的稀疏度预测的方法使所提DFT-SAMP 算法运行速率有明显的提升,在16 个导频时,算法效率相较于SAMP 算法提升约68%,在32 个导频时,提升约69%。
5 结论
针对可见光通信复杂的多径信道环境,引入压缩感知的方法进行MIMO-VLC 系统信道估计,并提出了DFT-SAMP 算法,通过基于DFT 的稀疏度预测方法提高了SAMP 算法运行速率,用更高效的方法保证系统通信质量。理论分析和实验结果表明:1)利用CS 算法进行MIMO-VLC 信道估计的性能明显优于LS 算法, 在导频数为16 时就具有优于LS 算法32 个导频时的性能,可降低50%的导频开销。2)DFT-SAMP 算法通过基于DFT 的稀疏度预测方法,在保证系统可靠性的同时减少了算法的运行时间,使DFT-SAMP 算法的运行速率相比SAMP 算法提升约69%。3)随着调制阶数M的增加,DFT-SAMP 算法相对于LS 算法的增益也越明显,在达到FEC 误码率阈值的情况下,调制阶数M=8 时,DFT-SAMP 算法相比LS 算法性能有3.5 dB 的提升,而在调制阶数M=64 时,则提升了10 dB,有利于系统通信效率的提升。

