FrFT-Bark 域特征提取与CNN 残差收缩网络心音分类算法
樊庆玲,杨宏波,郭 涛,张 伟,王威廉**
(1.云南大学 信息学院,云南 昆明 650500;2.云南省阜外心血管病医院,云南 昆明 650102)
据2020 年《中国心血管健康与疾病报告》显示,近年来中国心血管疾病患病率处于持续上升阶段,2018 年心血管疾病死亡率仍居首位[1].先天性心脏病(Congenital Heart Disease,CHD)简称先心病,是一种严重危害青少年身心健康的心血管疾病,心音的相关频谱内容是揭示CHD 的有用医学信息,因此研究心音包含的病理信息对于CHD 的早期诊断至关重要[2].用电子听诊器将心音的振动转变为电流,经放大后转化为心音图(phonocardiogram,PCG)[3],研究心音自动分类识别有助于提高CHD筛查的准确率和效率,使患儿及早得到医疗干预,降低其死亡风险.
心音分类算法重点在于特征提取和分类器的选择.目前从时域、频域和时频域角度提出了多种心音的特征提取方法.时域主要是提取信号的包络,然后根据包络分割定位,提取收缩期与舒张期时限和短时平均幅度差等时域特征[4];频域主要对信号进行某种变换,描述信号在频率方面的特性,频域图显示了一个频率范围每个给定频带的信号量,如小波变换[5]、傅里叶变换[6]等.无论从时域还是频域,提取特征都比较容易且方便进行量化分析,但是单独的时域或者频域特征不能充分反映心音信号的生理、病理信息,因此大多研究使用时频特征[7].由于心音本质上与语音信号相似,都为非线性非平稳信号[8],心音的分析常常借鉴语音处理的方法,语音特征提取方法包括短时傅里叶变换(Short-Time Fourier Transform,STFT)[9]、梅尔倒谱系数(Mel-Frequency Cepstrum Coefficient,MFCC)、梅尔频谱系数(Mel-Frequency Spectral Coefficient,MFSC)、Bark 倒谱系数(Bark-Frequency Cepstrum Coefficient,BFCC)、Bark 频谱系数(Bark-Frequency Spectral Coefficient,BFSC)等.
Milani 等[10]在150 例心音样本中分别提取时域、频域及时频域特征使用人工神经网络(Artificial Neural Network,ANN)对心音分类,分别得到0.9、0.833、0.933 的准确率.Chairisni 等[11]使用BFCC 特征和BP 神经网络对心音进行二分类达到0.791 6 的准确率.Kui 等[12]首先使用1 800 例心音样本用动态帧长方法,基于心动周期从心音信号中提取对数MFSC 特征,然后用卷积神经网络(Convolutional Neural Network,CNN)对MFSC 特征进行分类,最后采用多数投票算法得到最优分类结果,二分类准确率达到0.938 9,多分类问题准确率达到0.862 5.李伟等[13]未对心音进行分割,保留了心音更多的全局信息,准确率达到0.857.
以上研究都取得了较好的效果,但其心音样本的数量较少或未覆盖低龄儿童,这些算法的普适性及泛化性有待验证.文献[11]使用反向传播(Back Propagation,BP)神经网络进行分类识别,BP 神经网络存在局部极小化问题且算法收敛速度比较慢.文献[12]在特征提取前对心动周期进行分割,由于在噪声环境下很难准确分割出基本心音,给后续处理带来误差,同时也增大了算法的计算量.文献[13]虽保留了更多心音的全局信息,但其仅用CNN 和循环神经网络(Recurrent Neural Network,RNN)结合的网络直接对完整心音数据提取特征并做分类,准确率还有待提高.
为简化心音分类过程,充分挖掘心音信号所蕴含的生理、病理信息,进一步提升心音分类的准确率及算法的普适性,本文提出一种不依赖于去噪和分割的心音自动分类新算法:提取基于分数傅里叶变换Bark 域谱系数(Fractional Fourier Transform-Bark-Frequency Spectral Coefficients,FrFT-BFSC)的心音时频特征,同时在CNN 中引入深度残差收缩网络(Deep Residual Shrinkage Networks,DRSN)即CNN-DRSN 分类模型对特征进行验证.该模型通过软阈值算法自适应地保留与当前分类任务相关的特征信息,简化算法和计算量的同时提高了模型预测的准确率及稳定性.
1 方法分析
1.1 整体框架对PCG 信号分类识别的步骤一般包括预处理、特征提取和分类识别3 个部分,而预处理阶段一般是对心音进行去噪和分割.为简化心音分类流程并保留更多的生理信息,本文在不对心音进行去噪和分割的情况下,首先随机截取2 s 信号进行后续处理,2 s 中包含1~2 个完整的心动周期;然后提取心音的FrFT-BFSC 特征;最后在CNNDRSN 分类模型中训练和分类识别.实验结果表明该算法能达到较好的效果,算法框图如图1 所示.

图1 心音分类算法框图Fig.1 Block diagram of heart sound classification algorithm
1.2 实验数据本文研究所用心音数据集由课题组采集构建.课题组与云南省阜外心血管病医院合作,采集的异常心音样本来源于云南省阜外心血管病医院的临床患者,正常样本来源于云南省各地州开展CHD 免费筛查救治活动时的儿童.对于数据集的心音样本做以下说明:采集志愿者年龄分布在6 个月至18 岁;数据库中的所有样本都经心脏病专科医生确认,阳性病例均用超声心动图确诊;心音传感器使用的是The One 心音传感器(Thinklabs Medical LLC,美国),其采样频率为5 000 Hz,每一例心音样本采集时长均为20 s.
心音信号采集时,需在一个相对安静的环境(可有效减少环境噪声);志愿者需平躺且保持胸部裸露(减少传感器与衣服间的摩擦),将心音传感器放在临床心脏听诊的5 个部位采集信号.实验选取5 000 例心音样本,其中正常和异常(CHD)样本比例为1∶1.5 000 例样本按照0.65∶0.15∶0.2 的比例划分为训练集、验证集和测试集.
1.3 特征提取为挖掘更多PCG 的生理信息以获得最佳分类精度,本文提出一种FrFT-BFSC 特征,其能够充分提取PCG 的时频信息,是BFCC 特征的改进,特征提取示意图如图2 所示.

图2 特征提取示意图Fig.2 Schematic of feature extraction
特征提取的具体步骤如下:
步骤1预加重、分帧和加窗.预加重处理其实是将信号通过一个高通滤波器,可对因受到环境影响而抑制的心音信号高频分量进行补偿,使用预加重高通滤波器H(z),其计算公式如下:
式中预加重参数k取0.973 5,其能够有效抑制随机噪声,提高输出信噪比.
选用hamming 窗进行分帧加窗,窗长和窗移分别为512 和256 个采样点,得到38 帧信号.
PCG 的分量按在心动周期中出现的顺序可依次命名为S1、S2、S3、S4,通常情况下只能听到S1和S2,S3 和S4 一般听不到,表1 为心音各分量的持续时间[14].由于心音信号是非平稳信号,短时间内可将其视为平稳信号,且病理性杂音一般出现在收缩期[15],本文按照0.1 s 对预加重后的心音信号进行分帧,可最大限度捕获病理特征.因本文所用心音数据的采样率为5 000 Hz,故每一帧大小应为500 点,但500 个点不利于分数傅里叶变换(Fractional Fourier Transform,FrFT)的计算,因此确定帧长为512 点;为增强帧与帧之间的信号相关性,将帧移定为帧长的一半,故帧数为38 帧.

表1 心音分量的持续时间Tab.1 Duration time of heart sound component
步骤2计算FrFT.计算每帧信号的FrFT,以便获取更多的时频信息.
FrFT 是傅里叶变换的推广形式,若将信号的傅里叶变换看成信号在时间轴上逆时针旋转π/2到频率轴上,那么FrFT 可看成信号在时间轴上逆时针旋转任意角度后到u轴的分数阶Fourier 域上[16],即信号在时频面内以O为原点逆时针旋转任意角度α后构成的分数阶Fourier 域,如图3 所示.从信号的本质上来讲,FrFT 是一种时频分析方法,原因是其同时融合了信号的时域和频域信息.FrFT 能将信号转换到时间和频率之间的任何中间域,具有更灵活的时频表示.通过对帧级信号进行FrFT,此方法在处理非平稳信号中具有一定优势,其受噪声影响较小,抗干扰性能优于傅里叶变换[17].心音为非平稳信号,因此对心音帧级信号进行FrFT 能获得更多的有用时频信息.

图3 时频轴旋转α 角度的分数阶Fourier 域平面[19]Fig.3 Fractional Fourier domain plane with time-frequency axis rotated by α degree[19]
一维信号f(x)的a阶FrFT 从积分变换角度[18]的定义为:
式中:Fa是FrFT 算子,设α≠nπ,α=(aπ)/2,n为整数,则核函数K(ξ,x):
式中:α表示时频轴以O为原点逆时针旋转的角度.
式(2)可表述为信号f(x)的a阶FrFT,也可表述为信号f(x)在α角度下的FrFT.
根据FrFT 的性质,FrFT 的阶次a具有周期性,为了简化计算,一般取0.5≤a≤1.5,则可将(2)式改写为:
从公式(5)可以看出,FrFT 可通过信号先与一线性调频函数相乘,其次进行傅里叶变换,然后再与一线性调频函数相乘,最后乘以一复数因子得到.
不同的a值对应不同的时频特征,因此需要找到一个最优阶次a0,使信号经过FrFT 后能获得较多时频信息,在最优阶次a0下,FrFT 的幅值谱呈现能量集中特性,在ξmax处形成冲击,且该冲击峰值为各阶次变换下峰值的最大值,即
因此,可依据幅值谱峰值大小找到能量最集中的阶次.
为找到最优阶次a0,本文将阶次精度精确到0.001.首先计算在区间0.500≤a≤1.500 的幅值峰值,如图4(a)所示,可以看到它的峰值集中在阶次a=1.000 附近;接着在阶次a=1.000 附近分别计算区 间0.900≤a≤1.000 和区间1.000≤a≤1.100 阶次的峰值,如图4(b)和(c)所示,可以看出,在区间1.000≤a≤1.100 中,峰值呈下降趋势,而在区间0.900≤a≤1.000 中,阶次a=0.990 附近达到峰值;然后在区间0.990≤a≤1.000 中计算峰值,如图4(d)所示,当a=0.994 时,幅值达到最大,即最优阶次a0=0.994,故本文选用阶次a=0.994.

图4 不同阶次FrFT 幅值散点图Fig.4 Scatter plot of FrFT amplitudes for different orders
步骤3Bark 域尺度变换.通过Bark 滤波器组将得到的频谱映射到Bark 尺度,Bark 滤波器组中设置滤波器数为40.对于心音信号的频率,低频范围在3~5 Hz,高频范围在600~800 Hz,信号动态范围可达60~80 dB,而20 Hz 以下的频率人耳几乎听不见[20].人耳能接收到声音的高低和声音的频率是非线性的,Mel 频率尺度和Bark 频率尺度是比较常见的非线性频率尺度,后者比前者更适合人类心理听觉特性[21].图5 为24 个Bark 滤波器组成的频率响应分布图,Bark 域对低频具有放大作用、高频具有压缩作用,这一点从图中可以明显看出.不同中心频率的滤波器冲激响应幅度等高,在Bark 域中能够更加真实地反映人耳对信号产生的感觉.将分数傅里叶变换后的信号通过Bark 滤波器组,Bark 频率与实际频率存在反双曲正弦的关系[22],两者的转换关系式如下所示:

图5 Bark 滤波器组频率分布Fig.5 Distribution of Bark filter bank frequency
式中:FB(f)表示Bark 频率,f是实际频率.
步骤4取对数.计算每个滤波器输出的对数能量,得到特征维度为38×40 的FrFT-BFSC 特征值.
图6 为3 例正常和3 例异常样本的FrFT-BFSC特征图,纵坐标表示信号分帧后的信号帧数为时域,横坐标表示滤波器数为Bark 频域.其中异常信号的时频能量聚集,从图中可以看出两者有明显的差异,为提高分类精度提供了保证.
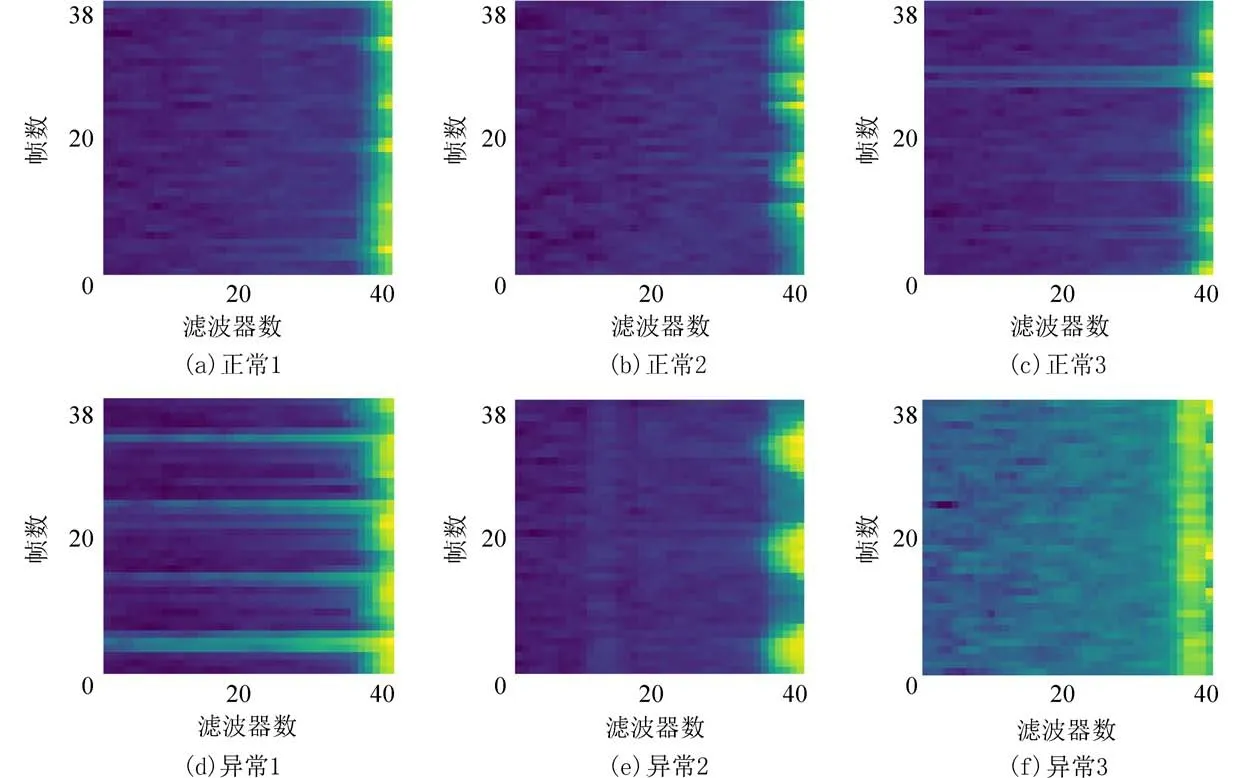
图6 FrFT-BFSC 特征图Fig.6 FrFT-BFSC feature map
1.4 分类模型随着深度学习的发展,大量研究考虑使用时频特征和深度神经网络架构相结合的分类模型[23].CNN 成为计算机视觉领域最常用的一种深度学习框架,它具有表征学习的能力,可以从输入信息中提取高阶特征.文献[10]、[12]、[23]等用CNN 对心音进行分类,都取得不错的效果.由于本文没有对数据进行去噪,而CNN 中卷积层主要是对输入数据提取特征,在处理含噪且有效信息不明显的数据时,卷积核提取特征可能存在由于噪声较大而特征信号较小无法检出的问题,这将导致输出层所具有的学习能力不够,以致无法正确区分样本的类型[24].DRSN 是2019 年Zhao 等[25]提出的一种改进的深度残差网络模型,用于处理含噪振动信号,是一种新的处理含噪数据的深度学习方法,在ResNet 中加入软阈值算法,使分类网络具有自适应对含噪数据设定阈值的能力,可有效对含噪数据进行区分.DRSN 模型结构如图7(a)所示,其组成基本要素残差收缩模块如图7(b)所示.残差收缩模块不仅有一个软阈值化函数作为非线性层,而且嵌入了一个子网络,对各个特征通道进行软阈值化.该模块所获得的阈值,并不是一个值而是一个向量,也就是特征图的每一个通道都对应着一个收缩阈值,即不同通道间阈值独立的深度残差收缩单元模块.
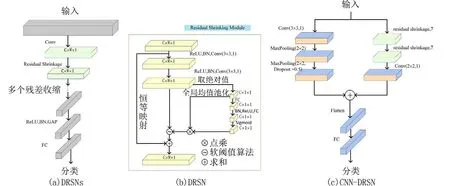
图7 CNN-DRSN 模型结构图Fig.7 Structure diagram of CNN-DRSN model
考虑到心音信号采集时也会引入一些环境噪声,为进一步有效利用特征信息,搭建CNN-DRSN分类模型如图7(c)所示,由CNN 分支和DSN 分支组成.该分类模型综合CNN 和DRSN 的优点,既可弥补CNN 学习能力不足以正确区分样本的缺点,又能保留与当前任务相关的特征信息,提高分类模型预测的准确率及模型的稳定性.为验证CNNDRSN 分类模型的可靠性,搭建CNN 进行对比,CNN 模型结构如图8 所示.

图8 CNN 模型结构图Fig.8 Structure diagram of CNN model
将1.3 节提取到维度为38×40 的FrFT-BFSC特征矩阵分别输入两种分类网络中,因所提特征维度较小,故不适合搭建深层网络,图7、8 中展示了CNN 和CNN-DRSN 结构图的详细参数.CNN 结构中含两个卷积层,选用线性整流函数(Rectified Linearunit,ReLU)作为激活函数;最大池化层在卷积层之后,其主要作用是选择保留池化核中最大的数值;在全连接层之前,需对特征进行展平(Flatten),主要是为了将参数过渡到全连接层;使用3 个全连接层,并用Dropout 和L1 权重正则化来防止模型过拟合;选用Adam 优化器和交叉熵损失函数(categorical_crossentropy)配置模型,初始学习率设置为0.001,并用softmax 作为最后一层的激活函数,它能将分类的结果以概率的形式展现出来,选取概率最大的结点作为最终输出.在CNNDRSN 模型结构中CNN 分支含一层卷积,DRSN分支含两层残差收缩层和一层卷积层,之后通过展平和全连接进行分类预测,同样选用Adam 优化器和交叉熵损失函数(categorical_crossentropy)来配置模型;输入网络的特征图经过取绝对值和全局均值池化之后变为一维向量,神经元的数量等于输入特征图的通道数量,便可让每个通道都具有独立的阈值,再输入两层全连接层,用softmax 作为最后一层的激活函数,初始学习率设置为0.000 5.阈值λc的计算公式如下:
式中:δc为第c层缩放到(0,1)之间的比例参数,i,j和c分别表示输入特征的宽度、高度和通道的索引,average 为平均值.
2 实验及结果
2.1 实验环境说明软件环境:编程软件为Pycharm 2021,编程语言为Python 3.7,所使用卷积神经网络和深度残差收缩网络均在TensorFlow 2.0框架中实现.硬件环境:中央处理器(AMD Ryzen7 5800H@3.2 GHz,RAM 为16 GB),独立显卡(NVIDIA GeForce RTX3060).所有实验均使用同一数据集且在同一台设备进行.
2.2 评估指标对于分类问题,常采用准确度(Accuracy,A)、灵敏度(Sensitivity,Se)、特异度(Specificity,Sp)、损失值(Loss,L)和F1 作为评价指标,前三者的定义式分别为式(9)~(11),使用的categorical_crossentropy 损失函数定义为式(12).
式中:TP表示异常心音样本被正确分类的数量,即真阳性;TN表示正常心音被正确分类的数量,即真阴性;FP表示正常心音被错误分类的数量,即假阳性;FN表示异常心音被错误分类的数量,即假阴性.式(12)中N表示测试样本数,yk表示第k个样本的真实值,yk'表示第k个样本的预测值.
F1 是精确率(Precision,P)和召回率(Recall,R)之间的调和平均数,常作为分类问题的一个综合性衡量指标,定义式如下:
2.3 结果分析为验证本文所提特征与改进网络模型的稳定性与泛化能力,将提取的不同特征分别放入CNN 和CNN-DRSN 分类模型中进行训练和测试.
首先探究滤波器组中滤波器数量对模型性能的影响,采用固定帧数、不同数量的Bark 滤波器的方式进行对比实验.Bark 滤波器的数量分别设置为24、32、40、64,得到的二维特征矩阵分别为38×24、38×32、38×40、38×64,在不同网络中的实验结果如表2 所示.由表2 可知,分类网络CNNDRSN 整体上比单独CNN 的效果更好.随着滤波器数量的增加,分类结果有一定的提升,但滤波器组数量增加到64 时,整体性能反而有所下降.原因可能是当滤波器数量逐渐增大时,能获得的有效信息逐渐增多,而当滤波器数量增加到一定数量后,滤波器组中心频率过于接近会影响滤波效果,导致模型整体性能下降.从表2 中可以看到,FrFT-BFSC(38×40)与CNN-DRSN 的组合模型整体效果最佳.

表2 不同参数下FrFT-BFSC 特征的心音分类结果对比Tab.2 Comparison of heart sound classification results with FrFT-BFSC features under different parameters
为验证本文所提FrFT-BFSC 特征的可靠性,与近几年常见的心音信号特征提取方法进行对比,如文献[11]、[12]、[23]的特征提取方法.其中所有特征维度均为38×40,并在两种不同的网络中训练和测试,对比实验结果如表3 所示.分析表3 可知,在不同的网络中,特征MFSC 和BFSC 比MFCC和BFCC 的效果更好,原因是后者在前者的基础上进行了离散余弦变换,使特征信息被压缩;而实验3-2 和3-4 验证了文献[21]所提Bark 频率尺度更适合人类心理听觉特性;FrFT-BFSC 特征是在BFSC特征上的改进,F1 作为分类问题的一个综合性衡量指标,由表2 和表3 可以看出,本文所提心音分类算法的F1 值最高,整体效果较其他特征好很多.实验3-10 是本文所提算法,其整体性能明显优于用CNN 作为分类器的模型.

表3 不同特征下心音分类的结果对比Tab.3 Comparison of heart sound classification results under different features
表4 为不同算法复杂情况对比,其中资源占比为GPU 显存占用率,运行时间为每一轮训练所需的时间.可以看出本文算法情况下显卡的性能得到充分的使用,GPU 资源占比越高,每轮运行的时间越少.

表4 不同文献算法复杂情况对比Tab.4 Comparison of complexity under different algorithms
设置训练迭代次数为70 次,该算法训练过程中准确率和损失值的变化曲线分别如图9(a)和9(b)所示,迭代次数在50 次左右时模型已经逐渐趋于稳定,其中验证集的准确率在0.88~0.90 附近摆动,验证集的损失值在0.3 左右.总体而言,FrFTBFSC 特征与CNN-DRSN 结合的模型性能更好.
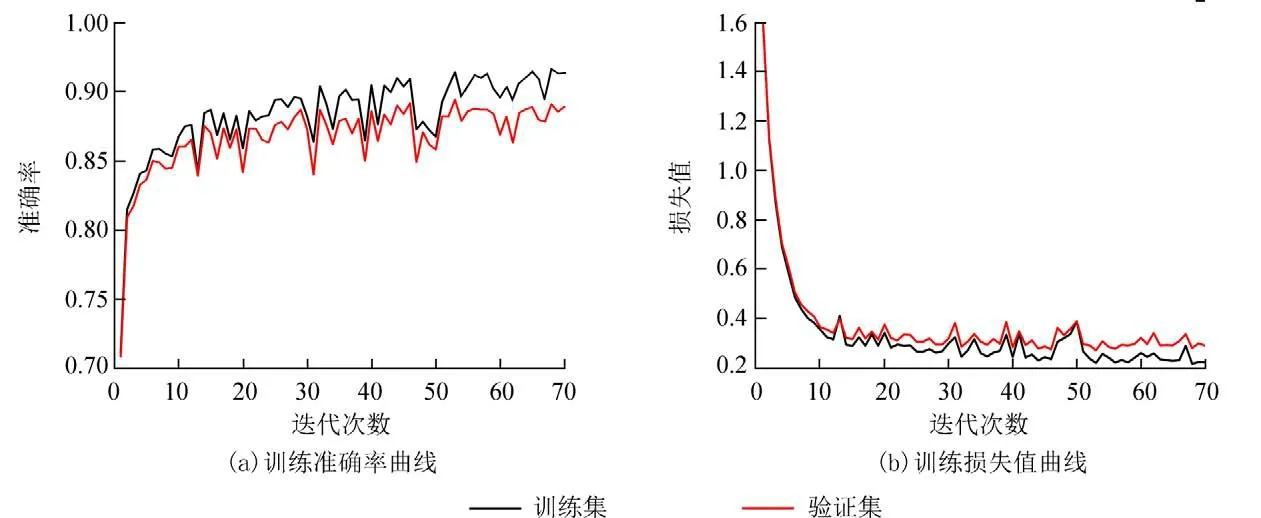
图9 模型训练准确率和损失值曲线图Fig.9 Curve of model training accuracy and loss value
通过以上实验结果分析,FrFT-BFSC(38×40)与CNN-DRSN 结合的算法综合性能优于其它算法,FrFT-BFSC 特征能充分提取心音信号的时频信息,CNN-DRSN 分类模型通过软阈值自动去除与当前任务无关的特征信息,从而达到较好的效果.本文所使用的数据样本更多且具有针对性,结果表明所提出的算法鲁棒性和泛化能力更强.
3 结束语
传统的听诊需依靠有经验的医生,而心音自动诊断能够在青少年CHD 筛查中帮助医生更加快速、准确地分辨出是否患CHD,从而更加高效地保障青少年身心健康.随着深度学习的发展,本文提出一种新的不依赖心音去噪和分割的FrFT-BFSC 特征提取方法,该特征更能反映PCG 的生理、病理特性;在改进的网络即CNN-DRSN 中进行训练及验证,并采用5 种常见的评估指标对模型进行评估.实验结果表明,该算法在较低复杂度、较少计算量的情况下得到0.925 的准确率,且不对PCG 进行去噪和分割能简化算法并提高算法可靠性.综合性能较以往的方法有明显提升,具有较强的鲁棒性和泛化能力,有望应用于先心病的临床初诊和筛查.本算法目前实现了对正常、异常心音进行二分类,尚未对何种病例进行多分类分析,这是今后研究的重点.

