基于钎焊残余应力的不锈钢芯板楼板性能研究*

舒兴平 李 珂 黄毅恒,2

(1.湖南大学土木工程学院,长沙 410082;2.南宁市建筑规划设计集团有限公司,南宁 530026)

0 引 言

不锈钢芯板是一种新型的建筑结构构件,它类似于航空航天领域中的蜂窝板结构[1]。不锈钢芯板是由上下两块不锈钢面板和一定数量的不锈钢芯管按特定的排列并用热风铜钎焊而成,如图1所示。它既具有传统钢结构轻质高强的特点,又具有不锈钢材料的抗腐蚀性和极佳的变形能力[2]。

不锈钢芯板的铜钎焊技术与传统的焊接工艺不同,在将板件送入热风钎焊炉前,先对芯管和面板进行点焊,确保在钎焊时面板和芯管的位置不会发生错动,再将装配好的不锈钢芯板整体送入钎焊炉中,经高温惰性保护气体加热,保证铜基钎料的充分融化,融化后的铜基钎料通过毛细作用会填充面板和芯管之间的间距。通过改变保护气体的温度,让炉中温度整体下降,使铜基钎焊处冷却凝固形成可靠的钎焊接头[3]。

对于钎焊接头而言,钎焊残余应力对其受力性能有着重要的影响[4]。目前,国内外对不锈钢芯板的钎焊残余应力的研究还很缺乏,故研究不锈钢芯板钎焊残余应力的大小及其分布形态对其工程应用和工业生产有着重要的指导意义。

本文拟采用钻孔法和X射线衍射法对25个不锈钢芯板单管试件(10个单管芯管试件和15个单管面板试件)进行钎焊残余应力的测定,并对试验数据进行整理归纳,提出钎焊残余应力建议简化分布模型。根据不锈钢芯板楼板三点弯曲试验[5]建立有限元模型,将所提出的建议简化模型应用至芯板楼板有限元模型中,对比考虑钎焊残余应力分布时芯板楼板的弯曲刚度与剪切刚度,验证钎焊残余应力简化分布模型的可靠性,并对芯板楼板剪切刚度的影响因素进行参数化分析,为不锈钢芯板楼板的结构设计与工程应用提供参考。

1 试验概况

1.1 材料力学性能

本试验中试件材料等级选用不锈钢S304L,且为同一批次生产。试验正式开始前,对不锈钢S304L进行材性试验,为后续钎焊残余应力值的计算提供参考。单调拉伸材性试验结果如表1所示,每组试验结果为3个相同尺寸试件的平均值。其中t为试件厚度;v为泊松比;E0为弹性模量;σ0.01、σ0.2分别为对应规定残余延伸率为0.01%和0.2%时的应力;σu为抗拉强度;εf为拉伸试验中测得的断后伸长率。4 mm试件的实测应力-应变曲线如图2所示,可以看出,不锈钢是一种典型的非线性材料[6]。

表1 单调拉伸试验实测结果Table 1 The measured results of tensile coupon test

图2 拉伸试验实测应力-应变曲线Fig.2 Measured stress-strain curve by tensile coupon test

1.2 试件设计

为便于不锈钢芯板的钎焊残余应力的测量,从不锈钢芯板整板中加工出一个单管试件作为测量试件。考虑到试验设备安装空间有限,在面板上芯管区域内部进行测量时,需先将芯管切割开仅留下面板。为了不破坏钎焊焊缝,线切割时需沿芯管长度方向从面板底部偏移5 mm左右处切割。试件的加工过程如图3所示。不锈钢芯板单元试件的基本几何尺寸符号见图4。其中,tp为面板厚度;bt为芯管外直径;tc为芯管壁厚;bp为面板宽度;hc为芯管高度。根据不锈钢芯板构件工业生产的常用尺寸,单管试件按其面板厚度分为5组,每组各5个试件,各组试件的具体几何尺寸参数见表2。

图3 试件加工过程Fig.3 Processing of test specimens

图4 试件基本几何尺寸符号示意Fig.4 Definition of the geometric dimensions of the specimen

表2 不锈钢芯板单管试件几何尺寸参数Table 2 The geometry parameters of the single-unit SSCP mm

1.3 残余应力测量方法

单管试件的面板残余应力采用钻孔法和X射线衍射法测量,因芯管壁厚较薄,采用钻孔法会造成额外的附加机械应变,影响测量结果的精度,故芯管部位仅用X射线衍射法进行测量。钻孔法试验设备型号为ZDL-Ⅲ型钻孔装置,X射线衍射法试验设备型号为IXRD残余应力分析仪。

钻孔法是基于测量试件钻孔前后应力差的一种半破坏性测定方法[7-8]。根据弹性力学知识可知,其计算式为：

(1c)

式中：σ1、σ2为主应力;A、B为应变释放系数;ε1、ε2、ε3分别为三向应变花所测得的三个方向的应变值。

X射线衍射法是依据Bragg衍射定律,通过检测金属晶体材料表面的衍射晶面间距来计算残余应力的一种非破坏性测定方法[9]。其计算式为：

(2)

2 建议简化分布模型的提出

2.1 钎焊残余应力试验结果

考虑到试验设备对测定环境和试件形状的要求,不锈钢芯板单管试件的钎焊残余应力测定包括芯管区域和面板区域两个部分。芯管区域的测点布置共分为3条测试路径,分别沿芯管圆周方向的0°(芯板整板长度方向)、90°和225°,每条测试路径上布置14个测点,各测点间隔为10 mm。面板区域的测点沿不锈钢芯板整板长度方向(纵向)进行布置,间隔为10 mm,单块面板上共计11个测点(由于钻孔法无法测量试件边缘的测点,则采用钻孔法时仅有9个测点),单管芯管试件和面板试件上的测点布置如图5所示。

a—芯管部位;b—面板部位。图5 单管试件的测点布置Fig.5 The layout of the measuring points

将试验所得数据进行归纳整理,按式(1)和式(2)计算获得钎焊残余应力值。其中,各组芯管试件的试验结果为2个平行试件的均值,各组面板试件的试验结果为3个平行试件的均值。各组试件的芯管区域和面板区域的钎焊残余应力大小及分布分别如图6和图7所示,图6中钎焊残余应力方向为沿芯管长度方向,图7中钎焊残余应力方向为沿芯板整板长度方向。从图中可知,单管的钎焊残余应力分布符合残余应力自平衡原则。

a—试件A1.5-0.3-150;b—试件A2.5-0.5-152;c—试件A4.0-0.5-155;d—试件A6.0-0.5-159;e—试件A8.0-0.5-163。图6 单管试件上芯管区域的钎焊残余应力分布 MPaFig.6 Brazing residual stress distribution in core tube of the specimen

a—面板厚度1.5 mm;b—面板厚度2.5 mm;c—面板厚度4.0 mm;d—面板厚度6.0 mm;e—面板厚度8.0 mm。图7 单管试件中面板上的钎焊残余应力分布 MPaFig.7 Brazing residual stress distribution in panels of the specimen

2.2 钎焊残余应力建议简化分布模型

为了进一步研究不锈钢芯板单元的钎焊残余应力,基于实测得到的芯板单管钎焊残余应力分布图,提出不锈钢芯板单管的钎焊残余应力的建议简化分布模型,如图8所示。

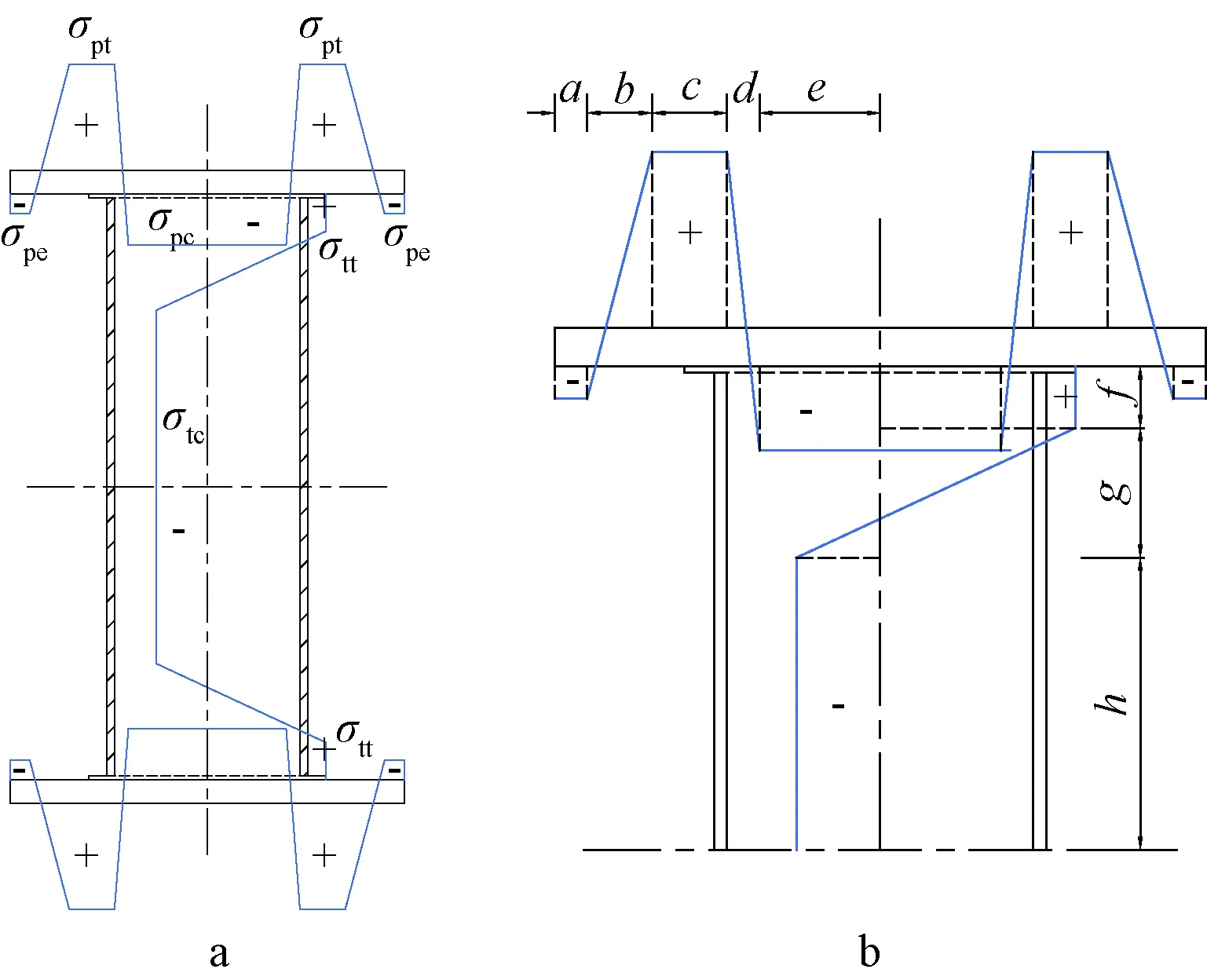
a—建议简化模型;b—钎焊残余应力分布范围。图8 简化钎焊残余应力分布模型Fig.8 Simplified brazing residual stress distribution model

根据实测的试验数据,简化分布模型假定芯管上下两底端的残余应力值同面板钎焊焊缝处的值相同,适当提升试件边缘的取值,并优化了钎焊残余拉、压应力的转换区宽度。不锈钢芯板单管的钎焊残余应力简化模型的取值如表3所示,结合图4的尺寸符号,建议简化模型的应力分布范围的取值如表4所示。

表3 不锈钢芯板单管的钎焊残余应力简化模型的建议取值Table 3 The recommended values of the simplified distribution model for the single-unit of SSCP

表4 简化分布模型的应力分布范围的建议取值Table 4 The recommended values of the stress distribution range for the simplified distribution model

3 钎焊残余应力简化分布模型拓展

3.1 建议简化分布模型与试验结果的比较

为了进一步研究所提出的建议简化模型,取面板和芯管区域的1/2结合试验测点的具体位置进行正则化,采用材料的名义屈服强度对钎焊残余应力值的平均值进行正则化,并将建议简化模型代入共同绘制成图9。

a—面板区域;b—芯管区域。图9 建议简化分布模型与试验数据对比Fig.9 Comparison between the proposed simplified distribution model and test data

从图9中可知,所提出的钎焊残余应力建议简化分布模型是连续的多段分布直线,其分布模型包络了试验结果的平均值,能较好地预测不锈钢芯板单元的钎焊残余应力分布形态,建议取值均偏安全。

3.2 建议简化分布模型的方向性

根据上述两种测定方法的基本原理可知,测得的钎焊残余应力具有方向性。不锈钢芯板单管试件的芯管为薄壁管状结构,且试件的钎焊焊缝也沿芯管周向分布,所以为了更加准确地描述不锈钢芯板的钎焊残余应力分布,需对简化分布模型进行方向性验证。

对芯管区域而言,同一试件上的三条测定路径上的钎焊残余应力分布形态基本相同。将芯管上钎焊残余拉应力与压应力峰值的最大值与最小值的差值汇总在表5中。可知：各试验分组的最大值与最小值误差均在14%以内,考虑到测量过程的敏感性与残余应力分布本身的离散性,可认为不锈钢芯板单管单元中,芯管上同一高度下沿其圆周方向分布的钎焊残余应力值相等。

为了进一步探究简化分布模型的方向性问题,对厚度为4 mm和6 mm的面板试件采用钻孔法进行测定,测定方向分为横向和斜向(与纵向成45°方向)。图10绘制了验证性测定试验结果与已有试验数据的对比。可知：不同方向的测定结果相互吻合良好,仅在残余拉、压应力转换区的应力值较为离散,由此可认为面板上的钎焊残余应力分布沿焊缝圆周方向相同。

a—4 mm厚试件横向对比;b—4 mm厚试件斜向对比;c—6 mm厚试件横向对比;d—6 mm厚试件斜向对比。图10 面板钎焊残余应力分布方向性对比 MPaFig.10 Comparison between the directions of the brazing residual stress in panels

4 不锈钢芯板楼板受力性能研究

黄毅恒对不锈钢芯板楼板进行了三点弯曲试验研究,如图11所示,并基于夹层板理论对不锈钢芯板楼板的受力性能作出了研究[5]。本文基于其试验结果,建立考虑钎焊残余应力简化分布的有限元模型,验证简化分布模型在芯板楼板中的适应性,并分析其对芯板楼板弯曲刚度与剪切刚度的影响。

图11 不锈钢芯板楼板三点弯曲试验Fig.11 The three-point bending test of SSCP

4.1 有限元模型的建立

采用有限元通用软件ABAQUS对不锈钢芯板楼板的三点弯曲试验的5组单向板试件进行建模,5组单向板试件的尺寸如表6所示。模型采用S4R壳单元缩减积分,模型的本构关系采用修正的Ramberg-Osgood模型,如图12所示。芯板楼板的单向板试件采用对边简支的边界条件,即固定铰支座(U1=U2=U3=UR1=UR3=0)、活动铰支座(U2=U3=UR1=UR3=0)。

表6 不锈钢芯板楼板三点弯曲试验试件尺寸Table 6 The size of SSCP floor three-point bending specimens mm

图12 修正后的Ramberg-Osgood材料本构模型Fig.12 The modified Ramberg-Osgood material model

钎焊残余应力可通过初始预应力场施加到芯板楼板有限元模型中[10],其残余应力分布输入按上述所提出的建议简化分布模型取值。由于简化分布模型基于不锈钢芯板单元,在有限元模型中需按照芯板单元的坐标逐步添加钎焊残余应力。钎焊残余应力的分量需要与部件的局部坐标系保持一致,确保输入正确方向的残余应力。由上述研究分析可知,芯板单管上芯管区域的钎焊残余应力以芯管圆心为轴,沿其圆周方向均匀分布,同一高度的残余应力值相同;面板区域的钎焊残余应力以面板几何中心向外辐射的多层次同心圆分布,相同半径区域的残余应力值相同,如图13所示。

a—单管钎焊;b—不锈钢芯板整板钎焊。图13 不锈钢芯板单元钎焊残余应力分布 MPaFig.13 The brazing residual stress distribution in stainless steel core plate

有限元模型采用位移控制的加载方式。加载压头采用解析刚体代替,在其上设置一个参考点,通过在参考点上施加竖向位移将荷载传递至试件上。在模型正式求解前需设置一个初始静力加载步,使引入的钎焊残余应力实现精确的自平衡。考虑钎焊残余应力分布的芯板楼板有限元模型的计算结果(变形缩放系数为2)如图14所示。

图14 有限元模型计算结果Fig.14 The calculation results of the finite element model

4.2 有限元结果与试验结果对比

将考虑钎焊残余应力的有限元计算结果与无钎焊残余应力的有限元计算结果同试验的荷载-位移曲线进行对比研究,结果如图15所示。其中,挠度指芯板楼板跨中的位移变形。可知：考虑钎焊残余应力的有限元模型能更准确地模拟三点弯曲试验中芯板试件的受荷载性能,验证了钎焊残余应力简化分布模型的可靠性,可为进一步研究其剪切刚度奠定基础。

a—试件PW1.5-1;b—试件PW1.5-2;c—试件PW2.5-1;d—试件PW2.5-2;e—试件PW4.0-1。 PW1.5-1-试验值; 有限元-考虑钎焊残余应力; 有限元-不考虑钎焊残余应力。图15 不锈钢芯板楼板三点弯曲试验与有限元荷载-位移曲线对比Fig.15 Comparison of the load-displacement curves of the test data of three-point bending and the finite element analysis of stainless steel core plate under vertical load

4.3 不锈钢芯板楼板刚度分析

基于夹层板理论[11],不锈钢芯板楼板的跨中最大挠度计算式和弯曲刚度计算式如下：

(3a)

D=E(hc+tp)2tp/[2(1-v2)]

(3b)

式中：wmax为跨中最大挠度;P为跨中集中荷载;a为支座跨径;b为芯板板宽;D为弯曲刚度;C为剪切刚度;E为杨氏模量;hc为芯管高度;tp为面板厚度;v为泊松比。

通过将两组不同支座跨径a1,a2的芯板的跨中挠度w1,w2代入式(3a)中,化简可得剪切刚度计算式为：

(4)

表7和表8中汇总了试验结果与有限元结果的对比,表中的弯曲刚度采用式(3b)计算,剪切刚度采用式(4)计算。由表中数据可知,考虑钎焊残余应力分布的有限元模型较不考虑钎焊残余应力分布的有限元模型计算结果误差更小,且误差均在5%以内,符合工程精度要求,进一步验证了简化分布模型的可靠性。考虑到试验试件的变形对诸多因素的敏感性和不确定性,总体上可认为考虑钎焊残余应力分布的有限元模型能更加准确地模拟芯板楼板的受力性能。

表7 弯曲刚度公式计算值与有限元结果计算值对比Table 7 Comparison between the calculated values of bending stiffness formula and finite element results

表8 剪切刚度公式计算值与有限元结果计算值对比Table 8 Comparison between the calculated values of shear stiffness formula and finite element results

5 参数分析

(5b)

图16 芯板楼板外伸三点弯曲计算模型Fig.16 The overhanging three-point bending model of SSCP floor plate

5.1 面板厚度tp

为进一步研究面板厚度对芯板剪切刚度的影响,建立面板厚度分别为1.5,2,2.5,3,3.5,4 mm的有限元模型,面板厚度tp对剪切刚度的影响如图17所示。可知：面板厚度tp对芯板楼板的剪切刚度影响较大,剪切刚度随面板厚度tp的增大而增大,考虑钎焊残余应力分布的有限元模型的剪切刚度略大于无钎焊残余应力分布有限元模型的计算结果。

图17 面板厚度tp对芯板楼板剪切刚度的影响Fig.17 The influence of panel thickness on shear stiffness of SSCP floor

5.2 芯管壁厚tc

为研究芯管壁厚变化对芯板楼板剪切刚度的影响,选取PW2.5-1有限元模型,建立芯管壁厚分别为0.5,0.6,0.7,0.8,0.9,1.0 mm的有限元模型进行计算,不同芯管壁厚tc的有限元计算结果如图18所示。可知：随着芯管壁厚的增大,芯板的剪切刚度呈上升趋势,在芯管壁厚不大时,剪切刚度几乎无差别;芯管壁厚从0.7 mm开始增加时,考虑钎焊残余应力的剪切刚度大于无钎焊残余应力的剪切刚度。

图18 芯管壁厚tc对剪切刚度的影响Fig.18 The influence of the wall thickness of core tube on shear stiffness of SSCP floor

5.3 芯管高度hc

芯管高度取100,125,147,175,200 mm,基于PW2.5-1模型对芯管高度建立有限元模型,有限元模型计算结果如图19所示。可知：不考虑钎焊残余应力的有限元模型的剪切刚度随芯管高度的变化不大,考虑钎焊残余应力的有限元模型的剪切刚度随芯管高度变化呈上升趋势,但在芯管高度为200 mm时,剪切刚度略微下降。主要原因是芯管高度的变化影响了芯管区域钎焊残余应力的分布,导致了剪切刚度的变化。

图19 芯管高度hc对剪切刚度的影响Fig.19 The influence of the height of core tube on shear stiffness of SSCP floor

5.4 芯管外径d

选PW2.5-1有限元模型为基准,芯管外径选取31,41,51,61 mm,建立新的芯板楼板有限元模型进行计算,计算结果如图20所示。可知,芯管外径对剪切刚度的影响较大,主要原因是芯管外径的增加会缩小芯管之间的面板净距,面板上的这部分净距主要影响剪力作用下芯板单元的位移变形,所以剪切刚度会提高;考虑钎焊残余应力的计算结果大于无钎焊残余应力的计算结果。

图20 芯管外径d对剪切刚度的影响Fig.20 The influence of the diameter of core tube on shear stiffness of SSCP floor

综上可知,考虑钎焊残余应力分布时模型的计算剪切刚度通常大于不考虑钎焊残余应力分布时的计算剪切刚度,其主要原因是芯板楼板受跨中集中荷载时,芯管端部靠集中力一侧主要受压,而芯管端部的钎焊残余拉应力会抵抗外荷载作用下的压应力,此时芯管的变形量会减少,从而导致了芯板跨中总挠度减少,进而提高了计算剪切刚度。

6 结束语

对25个不锈钢芯板单管试件采用钻孔法和X射线衍射法进行钎焊残余应力的测定,提出其钎焊残余应力建议简化分布模型,并在不锈钢芯板楼板三点弯曲试验的有限元模型中考虑钎焊残余应力的分布,得到如下结论：

1)实测的不锈钢芯板单管的钎焊残余应力分布呈双轴对称的特点,简化分布模型中的钎焊残余应力峰值均低于材料的名义屈服强度,钎焊残余拉应力和压应力的建议峰值分别为0.6σ0.2和0.3σ0.2,钎焊残余拉、压应力转换区的范围较窄。

2)不锈钢芯板单管上芯管区域的钎焊残余应力分布以芯管中心为轴,同一高度下的残余应力值相等,面板区域的钎焊残余应力以面板几何中心向外呈辐射状分布。不锈钢芯板整板的钎焊残余应力分布由各单管单元的钎焊残余应力按其生产工艺排列组合而成。

3)考虑钎焊残余应力分布的有限元模型能够更准确地模拟不锈钢芯板楼板的受力性能,证明了所提出的建议简化分布模型的可靠性。

4)考虑钎焊残余应力的分布能够更加精确地计算出芯板楼板的剪切刚度,面板厚度、芯管壁厚和芯管外径是影响芯板楼板剪切刚度的主要因素。不考虑钎焊残余应力时,芯管高度对芯板楼板的剪切刚度几乎没有影响,但考虑钎焊残余应力分布时,芯板的剪切刚度会发生变化。