三种泥沙扩散系数模型对双吸离心泵内固液两相流流场计算的影响

张自超，李延频，张兰金，陈德新

三种泥沙扩散系数模型对双吸离心泵内固液两相流流场计算的影响

张自超，李延频※，张兰金，陈德新

（1. 华北水利水电大学能源与动力工程学院，郑州 450045；2.华北水利水电大学河南省流体机械工程技术研究中心，郑州 450045）

作为模拟双吸离心泵内固液两相流的一种常用方法，欧拉-欧拉法中的泥沙扩散系数常通过多种模型进行计算。为选择适宜的泥沙扩散系数模型进而提高固液两相流数值计算的精度，该研究采用3种常见泥沙扩散系数模型Non-diffusion coefficient model（NON-DC）；Diffusion-in-volume of fluid model（Diffusion-in-VOF）；Diffusion coefficient affected by particle diameter and particle concentration model （DC-PDPC），在25、100和200 μm 3种含沙粒径和不同流量（0.6和1.0倍额定流量）条件下，对双吸离心泵内固液两相流场进行数值模拟，分析其对泵内固相浓度和固相速度的定常和非定常结果的影响。结果表明：1）当颗粒粒径不大于100 μm时，3种模型计算得到的双吸离心泵内固液两相流的固相浓度和速度定常结果基本相同；当颗粒粒径大于100 μm时，定常结果有所差异，随着颗粒粒径的增大，差异逐渐增大，差别最大可达60%。2）在不同颗粒粒径的条件下，采用3种模型得到的固液两相流场的固相浓度和速度非定常结果差异较大，且随着颗粒粒径的增大，差异逐渐增大，差别最大可达30%。含沙颗粒粒径不大于100 μm时，3种模型得到的定常结果基本相同；而大于100 μm时，定常结果差异较大；同样地，在不同含沙粒径条件下的非定常计算结果也差异较大，需要选择合适的泥沙扩散系数模型。3）定常计算时，当颗粒粒径不大于100 μm时，推荐NON-DC模型；随着颗粒粒径的增大，推荐使用DC-PDPC模型；当非定常计算时，推荐使用DC-PDPC模型。研究为准确地进行离心泵内固液两相流数值计算提供参考。

泥沙；数值分析；模型；双吸离心泵；扩散系数模型；定常；非定常

0 引 言

双吸离心泵广泛应用于黄河沿岸的灌溉泵站中[1]，过泵黄河水泥沙含量较高[2-3]，主要以悬移质小颗粒为主[4-5]，水泵的过流部件普遍存在磨损问题[6]，严重影响水泵的安全稳定运行。因此，准确计算双吸离心泵内的固液两相流场对研究双吸离心泵的磨损规律具有重要的意义。

针对悬移质小颗粒的试验不易开展[7]，目前试验主要针对大粒径颗粒[8]。数值模拟是研究固液两相流的重要方法[9-11]，而欧拉-欧拉方法是一种常用的两相流数值计算方法[12-13]。该方法中，表达两相间相互作用的项是通过模化得到的，进而产生了阻力模型和泥沙扩散系数模型。研究表明[14-18]，不同阻力模型的适用条件不同。泥沙扩散系数模型也是一个表达两相间相互作用的重要模化量。泥沙扩散系数用于描述泥沙扩散速度，相当于浓度梯度为1 mol/L时的泥沙扩散通量[19]，是影响固相体积浓度分布和输移的重要因素[20]。目前，基于不同理论的泥沙扩散系数计算模型包括3类[21-25]：1）类比水流涡黏性系数的半经验模型；2）基于颗粒扩散的半经验半理论模型；3）基于两相流理论的扩散模型。其中，基于类比水流涡黏性系数的半经验模型形式简单、应用较多，可以用于三维流场的数值模拟和计算[26]。前人在应用这类模型时基于不同的方法考虑了颗粒粒径的影响，构建了以下4种泥沙扩散系数模型：NON-DC模型（non-diffusion coefficient model）、Diffusion-in-VOF模型（diffusion-in- volume of fluid model）[27]、DC-PDPC模型（diffusion coefficient affected by particle diameter and particle concentration model）[28]和2DSF-DC模型（diffusion coefficient for two- dimensional surface flow model）[20]。其中，NON-DC模型不考虑浓度梯度的影响[28]；Diffusion-in-VOF模型认为含沙体积和颗粒粒径对流体湍流结构的影响是恒定的[27]；DC-PDPC模型考虑了颗粒动态尺度对湍流强度的影响[28]；2DSF-DC模型是针对含沙体积浓度较高时的二维明槽流动提出的[29]，因使用时无法确定三维问题的混参长度[20,26]，因此不能有效用于三维两相流数值计算，在本文中排除对该模型的研究。

前人研究了泥沙扩散系数对固液两相流流场的影响。谭泽宇等[30]针对振荡流层移输沙条件下的悬移层泥沙计算，汇总了已有的试验数据，采用曲线拟合方法得到相应的泥沙扩散系数，并得到泥沙在垂向的分布。ABDELALI等[31]提出了一种预测明渠流中悬移质泥沙浓度垂直分布的泥沙扩散系数模型，发现该模型的计算值与试验数据吻合较好。DEBASISH等[32]研究了颗粒浓度对泥沙和湍流扩散系数的影响，并通过二者之比定义的湍流施密特数来反映该影响，进而提出了改进模型，结果表明改进模型与前人提出的模型相比，误差较小。张自超等[28]研究了NON-DC模型、Diffusion-in-VOF模型和DC-PDPC模型对圆管内固液两相流数值计算结果的影响，发现3种模型对固相浓度分布有明显的影响，而DC-PDPC模型具有较高的计算精度。刘涛等[33]采用经验泥沙扩散系数对波浪条件下悬移质泥沙分布特性开展数值模拟，较好地解决了泥沙扩散系数难确定的问题。左利钦等[34]针对波浪边界层高含沙层特性，提出了不同床面波浪作用下的时均泥沙扩散系数表达式，预期可应用于二维和三维泥沙数值模拟。郭玉臣等[35]通过现场试验研究了倾倒区倾倒过程泥沙输运过程，建立了倾倒过程二维泥沙输运扩散数值模型，并对一些主要参数进行了计算和率定，结果发现模型参数率定后得到的计算结果更准确，为海洋倾倒区选划泥沙扩散系数模型参数的选择提供了参考。

综上，选择不同的泥沙扩散系数模型对固液两相流的数值计算结果具有一定的影响，而现有研究多关注于圆管流、明渠流和振荡流层移输沙条件下的固液两相流动。与双吸离心泵内的固液两相流对比，这些流动较简单、流动单一、脉动较小。由于叶轮的高速旋转，双吸离心泵内的流动速度大，流场复杂，脉动强烈，这与圆管、明渠流以及层移输沙条件下的流场明显不同。而泥沙扩散系数模型对双吸离心泵内固液两相流的影响研究未见报道。

因此，为选择适宜的泥沙扩散系数模型进而提高固液两相流数值计算的精度，本文选择3种模型（NON-DC模型、Diffusion-in-VOF模型和DC-PDPC模型），研究其对双吸离心泵内固相浓度和固相速度的定常和非定常结果的影响，以期为准确地进行双吸离心泵内固液两相流数值模拟提供参考。

１ 欧拉-欧拉两相数值模拟方法

1.1 控制方程

经过雷诺时均化处理的欧拉-欧拉两相流数值模拟方法中出现了时均的两相体积分数与两相速度脉动关联项。通过引入泥沙扩散系数，建立关联项与浓度梯度的关系[28]，代入时均化的固液两相连续方程中，最终得到连续方程和动量方程如下：

式中α为相的体积浓度，其下标=时为液相，=时为固相，且α+α=1；ρ为相的密度，kg/m3；为时间，s；v为相方向的时均速度，m/s；x,x,为、、2个坐标分量；为泥沙扩散系数；v为相方向的时均速度，m/s；为压强，Pa；μ为相动力黏度，Pa·s；μ为相时的湍动黏度，Pa·s；λ为相的雷诺应力，Pa；g为体积力，N；F为相间作用力，N。

1.2 泥沙扩散系数模型

式（1）中值采用类比水流涡黏性系数的半经验模型得到[26]：

1）NON-DC模型

忽略泥沙扩散系数的影响，认为泥沙的扩散不是由浓度梯度引起的[28]：

2）Diffusion-in-VOF模型

认为颗粒的脉动小于液相的脉动[27]，流体湍流结构对泥沙扩散系数的影响是恒定的[13]。根据Hinze-Tchen公式得到系数，系数取常数。

式中τ为颗粒弛豫时间，s；τ为液相的湍动时间尺度；为液相湍动能，m2/s2；ε为液相湍动能的耗散率；R是固相颗粒雷诺数；C为经验常数；d是固相颗粒粒径，m。

3）DC-PDPC模型

2 计算对象和设置

2.1 计算对象

本文的研究对象为山东双轮泵业生产的GS160-Ⅰ双吸离心泵，运行在山西尊村二级提灌泵站，其实际的几何参数、运行参数及过泵泥沙参数如表1所示。经调研，黄河沿岸离心泵运行中过泵泥沙颗粒具有以下特点：全年平均颗粒粒径为5～50 μm，汛期平均颗粒粒径可达200 μm。因此，本文设置25、100和200 μm 3种粒径开展不同粒径泵两相流数值计算。

表1 双吸离心泵几何参数及过泵泥沙参数

2.2 网格及边界条件

对研究对象计算网格进行网格无关性检查，网格无关性检查如图1a所示，得到各部分的网格单元数分别为：叶轮60万；吸水室56万；压水室40万；叶轮前后腔水体6.5万；进口延长段4.5万；出口延长段5.5万；总计172.5万。双吸离心泵计算域及网格划分情况如图1b所示。

图1 双吸离心泵网格无关性检查及网格

计算模型为欧拉模型，采用RNG-湍流模型（renormalization group-model）[36]。采用Dispersed turbulence model湍流多相流模型[28,37]。相间阻力模型采用Wen-Yu模型，该模型通常用于固相体积分数小于20%的情况[38]。泥沙扩散系数模型分别采用NON-DC模型、Diffusion-in-VOF模型和DC-PDPC模型。

计算域采用速度进口，分别设定固液两相速度和固相体积分数；出口采用自由出流；过流部件内壁面，不考虑粗糙度，设为光滑壁面，对液相采用无滑移壁面边界条件，对固相采用自由滑移壁面边界条件，近壁区采用标准壁面函数。

现有对离心泵非定常特性的数值研究表明[39-41]，非定常计算的时间步长为/120（为旋转周期，s）时，可以计算得到较准确的非定常结果。本研究为122.448×10-3s，因此，非定常计算时间步长为10.204×10-4s，总共计算时间为10。

2.3 监测点布置

为了研究固相参数的非定常特性，分别在叶片和蜗壳壁面上设置监测点。根据本课题组前期对双吸离心泵叶轮内泥沙磨损非定常特性的研究[39]，叶片吸力面、叶片压力面和蜗壳内的固相颗粒非定常特性分别具有相似的脉动特性。因此，在叶片吸力面和压力面中间位置各设置1个监测点，分别用于研究叶片吸力面和压力面的固液两相流场非定常特性。蜗壳隔舌处的动静干涉较强烈，需设置1个监测点，并在与隔舌呈180°的位置设置1个监测点。各监测点位置分别如图2和图3所示。分别在叶片吸力面和压力面壁面上各设置1个监测点，S1和P1分别位于叶片吸力面和压力面的中间位置，叶片上的监测点随叶片一起旋转。分别在蜗壳隔舌和螺旋角180°的壁面上设置监测点V1和V2。

图2 叶片上监测点S1和P1设置示意图

图3 蜗壳上监测点V1和V2设置示意图

各监测点监测的固相参数为固相速度和固相浓度，由于固相浓度是标量，而固相速度大小是影响磨损的主要因素，因此，各监测值只记录参数的大小，不监测方向。

3 数值模拟验证

3.1 验证方法

3.1.1 双吸离心泵外特性试验

试验时过泵泥沙的平均固相颗粒粒径为25 μm，在该含沙工况下验证双吸离心泵的扬程、效率的计算值和试验值，在尊村二级站进行水泵外特性现场试验。试验时，在水泵进出口布置压力脉动传感器，用于采集进出口的压力；在出口布置电磁流量计，用于采集流量；功率由布置在轴上的扭矩测速仪测量得到。通过控制出口阀门来获得不同的流量，进行了3种流量工况的试验。由于本文进行数值模拟研究，因此，数值计算时，采用DC-PDPC泥沙扩散系数模型进行了5种流量工况的计算，分别为0.4Q、0.6Q、0.8Q、1.0Q、1.2Q，其中Q为额定流量，m3/s。

3.1.2 固液两相流计算验证试验

由于固液两相流的流场计算较复杂，关系到固液两相的计算结果，因此需要对固液两相流的流场进行验证。双吸离心泵的结构复杂，固液两相流试验不易开展，因此本文选用文献[42]中具有固相浓度试验值的一个圆管对固液两相流的计算结果进行验证，计算对象如图4所示，图中线1为距离圆管进口3/4的竖直线，用于验证固相浓度分布。计算模型、设置等与本文双吸离心泵数值计算的相同，也采用DC-PDPC泥沙扩散系数模型进行数值计算。圆管参数和固相参数分别为：管径D=0.15 m，管长=3 m，进口速度v=3 m/s，进口固相体积浓度α=15%。固相颗粒粒径d=90 μm，固相颗粒密度ρ=2 650 kg/m3。

纵轴为线1的竖直方向位置=/D，为线1上点的坐标值与管径D的比值；横轴为固相体积浓度相对值α，根据式（11）计算固相浓度相对值。

式中α为固相浓度相对值；α为固相体积浓度，%；α为进口固相体积浓度，%。

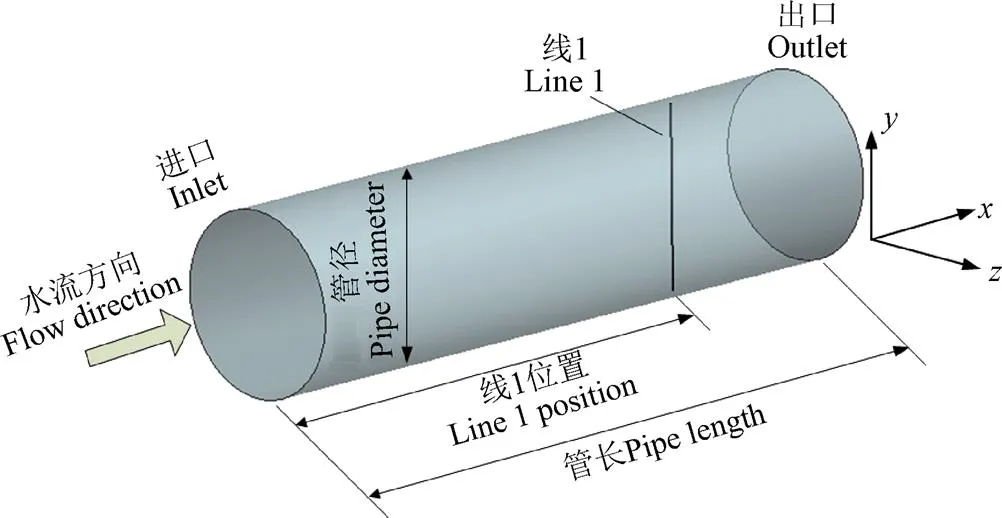
图4 水平圆管示意图

此外，为了便于对比分析固相速度分布的计算结果，根据式（12）进行固相速度的计算和分析。

式中v为固相速度相对值；v为固相速度，m/s；2为叶轮出口圆周速度，m/s。

3.2 结果与分析

3.2.1 外特性验证

过泵泥沙平均固相颗粒粒径为25 μm时双吸离心泵的扬程、效率的计算值和试验值，如图5所示。由图可知，扬程计算值与试验值的最小相对误差为1.9%，最大相对误差为3.6%；而效率计算值与试验值的最小相对误差为2.1%，最大相对误差为2.1%。由此可知，虽然外特性计算值与试验值存在一定的误差，但整体分布比较接近，具有可接受的误差范围，计算结果较可靠。

注：Q为流量，m3·s-1；Qn为额定流量，m3·s-1。

3.2.2 固液两相流计算的验证

图6给出了线1上的固相浓度计算值与试验值的对比。由图可知，固相浓度分布的计算值和试验值分布基本一致，整体趋势较吻合，相差不大，最大相对误差为9.5%，最小相对误差为0.1%，在可接受的范围内。由此可知，本文采用的固液两相流计算模型和设置均是合理的，计算得到的固液两相流场是准确、可靠的，可以用于进一步分析和研究。

注：竖直方向位置为y*=y/Dp，为坐标y值与管径Dp的比值。

4 数值模拟方法与结果分析

4.1 数值模拟方法

固相浓度和固相速度是固液两相流数值计算中2个非常重要的参数，因此，对这2个参数进行分析。根据黄河沿岸双吸离心泵的运行规律，选用0.6Q和1.0Q2个典型工况进行分析。为了研究不同颗粒粒径对计算结果的影响，对过泵泥沙中含沙粒径25、100和200 μm 3种颗粒的流场特性进行对比分析。

本部分需要分析3种泥沙扩散系数模型对叶轮内固相浓度和固相速度的定常计算结果的影响。为了便于分析，分别在叶轮内选取2个环线，以分析环线上的固相浓度和固相速度分布，2条环线的位置如图7所示。

注：θ为环线上点与隔舌之间的角度，(°)。

图7中，环线1和环线2分别位于叶轮内直径和/2处，2条环线均位于前后盖板之间的中间位置。环线的起始位置为隔舌位置，环线上点与隔舌位置之间的角度记为，从隔舌开始沿着水流方向分析环线上点的参数分布。

为了对比分析3种泥沙扩散系数模型对双吸离心泵内固相浓度和固相速度的非定常计算结果的影响，选取图2中叶片吸力面和压力面上的S1和P1点以及图3中蜗壳内V1和V2点4个监测点上固相速度和固相浓度的非定常数据进行分析。

4.2 结果与分析

4.2.1 1.0Q额定流量工况

1）固相浓度定常和非定常计算结果

图8给出了额定工况下，3种颗粒粒径时基于不同泥沙扩散系数模型得到的环线上固相浓度定常结果对比。由图可知，额定工况下，在同一颗粒粒径时，3种泥沙扩散系数模型在叶轮内计算得到的固相浓度分布的定常结果相对偏差小于2‰，基本重合。这说明，额定工况下，3种泥沙扩散系数模型对双吸离心泵内固液两相流的固相浓度分布的定常计算结果影响不大。

注Note：NON-DC, Non-diffusion coefficient model; Diffusion-in-VOF, Diffusion-in-volume of fluid model; DC-PDPC, Diffusion coefficient affected by particle diameter and particle concentration model.

图9给出了额定工况下，不同粒径时，3种泥沙扩散系数模型计算得到的各监测点上固相浓度非定常结果对比。由图可知，相比于定常计算结果，在同一颗粒粒径时，不同监测点上，3种泥沙扩散系数模型计算得到的固相浓度非定常结果有所不同。在同一监测点上，随着颗粒粒径的增大，3种泥沙扩散系数模型计算得到的固相浓度非定常结果差别增大，相差最大达1.5%。这说明，额定工况下，不同的泥沙扩散系数模型计算得到的双吸离心泵内固液两相流的固相浓度分布的非定常计算结果差异较大，而且随着颗粒粒径的增大，差异逐渐增大。

2）固相速度定常和非定常计算结果

图10给出了额定工况下，3种颗粒粒径时不同泥沙扩散系数模型得到的环线上固相速度定常结果对比。由图可知，额定工况下，在同一固相颗粒粒径时，3种泥沙扩散系数模型在叶轮内计算得到的固相速度分布的定常结果相差不大，相差最大为3‰，基本重合。这说明，额定工况下，3种泥沙扩散系数模型对双吸离心泵内固液两相流的固相速度分布的定常计算结果影响不大。

注：t为时间，s；T为叶轮旋转周期，s。

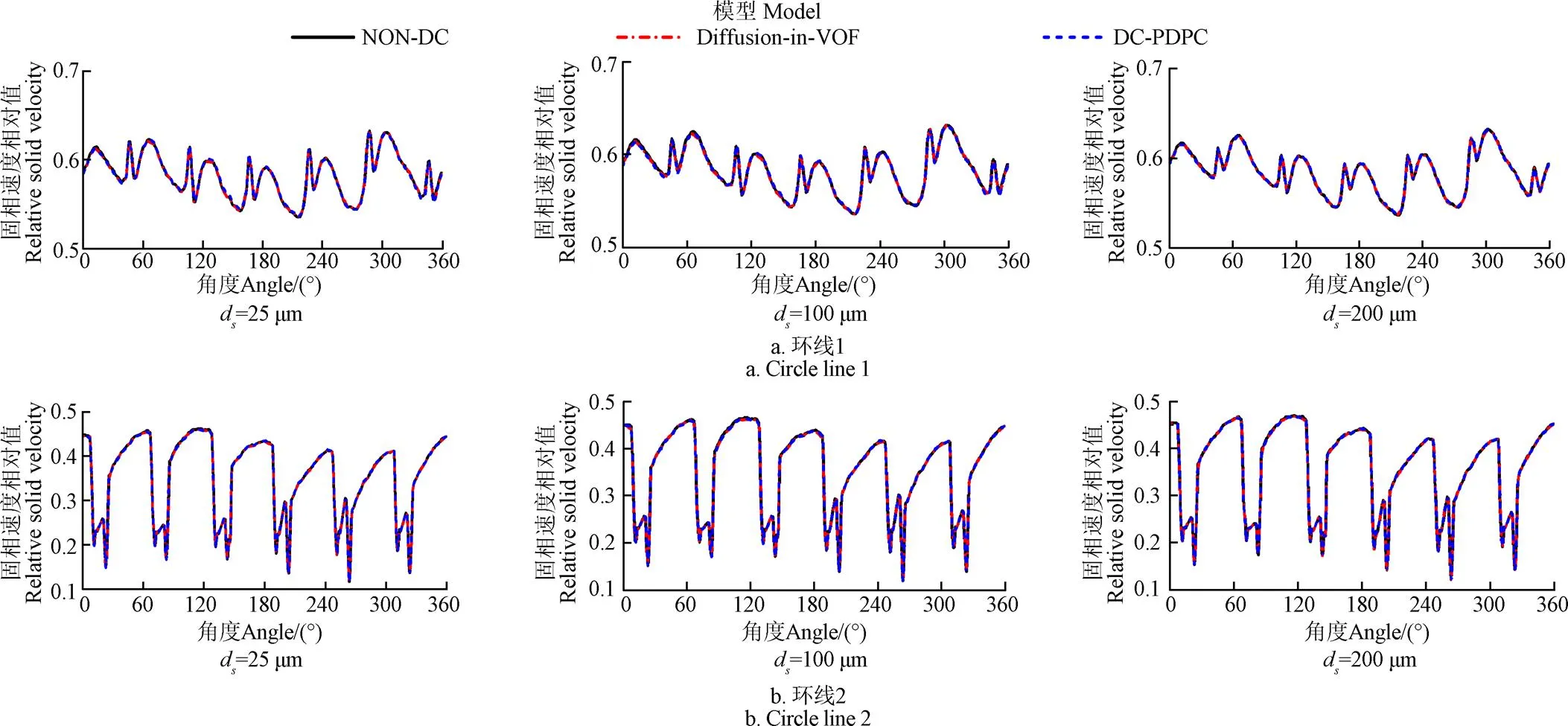
图10 额定工况下，不同粒径（ds）时不同泥沙扩散系数模型得到的环线上固相速度相对值定常结果对比

图11给出了额定工况下，不同粒径时，3种泥沙扩散系数模型计算得到的各监测点上固相速度非定常结果对比。由图可知，额定工况下，在同一固相颗粒粒径时，3种泥沙扩散系数模型在不同监测点上计算得到的固相速度的非定常结果相差不大，差别最大为1.3‰，基本重合。这说明，额定工况下，3种泥沙扩散系数模型对双吸离心泵内固液两相流的固相速度分布的非定常计算结果影响不大。

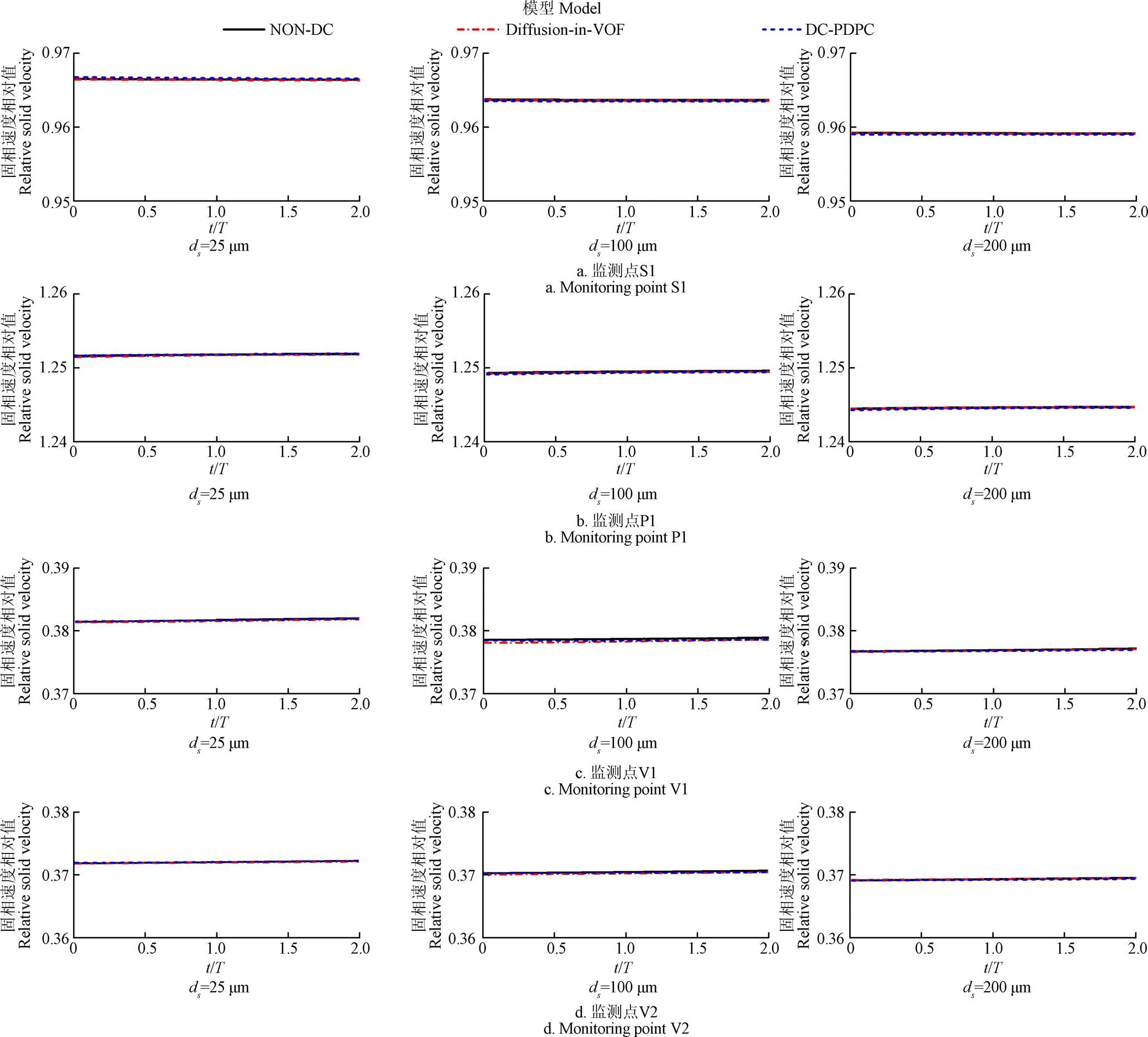
图11 额定工况下不同粒径（ds）时不同泥沙扩散系数模型得到的各监测点上固相速度相对值非定常结果对比

综上所述，额定工况下，在不同粒径颗粒条件下，不同的泥沙扩散系数模型计算得到的双吸离心泵内固液两相流的定常计算结果均基本相同，泥沙扩散系数模型对固液两相流的定常计算结果影响不大，NON-DC模型结构简单，推荐使用；但是，不同的泥沙扩散系数模型得到的固相浓度分布非定常结果差异较大，而且随着颗粒粒径的增大，差异逐渐增大，推荐使用DC-PDPC模型，该模型考虑了颗粒粒径对固相浓度的影响。

4.2.2 0.6Q额定流量工况

1）固相浓度定常和非定常计算结果

图12给出了小流量工况下，3种颗粒粒径时不同泥沙扩散系数模型得到的环线上固相浓度定常结果对比。由图可知，小流量工况下，3种泥沙扩散系数模型计算得到的叶轮内固相浓度分布的定常结果在不同固相颗粒粒径时表现出不同的特性。由图可知，当颗粒粒径分别为d=25 μm和d=100 μm时，同一颗粒粒径条件下，3种泥沙扩散系数模型计算得到的叶轮内固相浓度分布的定常结果有所差别，但整体上比较吻合。当d=200 μm时，3种泥沙扩散系数模型计算得到的叶轮内固相浓度分布的定常结果差异较大，差别最大可达60%。这说明，小流量工况下，不同的泥沙扩散系数模型计算得到的双吸离心泵内固液两相流的固相浓度分布的定常结果在小粒径颗粒时，差别不大，随着颗粒粒径的增大，差异逐渐增大。

图13给出了小流量工况下，不同粒径时，3种泥沙扩散系数模型计算得到的各监测点上固相浓度非定常结果对比。由图可知，相比于定常计算结果，在同一颗粒粒径时，3种泥沙扩散系数模型计算得到的固相浓度非定常结果差别较大，相差最大可达30%。在同一监测点，随着颗粒粒径的增大，3种泥沙扩散系数模型计算得到的固相浓度非定常结果差别逐渐增大。这说明，小流量工况下，不同的泥沙扩散系数模型对双吸离心泵内固液两相流的固相浓度分布的非定常计算结果影响较大，而且随着颗粒粒径的增大，固相浓度计算结果的差异逐渐增大。

图12 小流量工况下不同粒径（ds）时不同泥沙扩散系数模型得到的环线上固相浓度相对值定常结果对比

图13 小流量工况下不同粒径（ds）时不同泥沙扩散系数模型得到的各监测点上固相浓度非定常相对值结果对比

2）固相速度定常和非定常计算结果

图14给出了小流量工况下，3种颗粒粒径时不同泥沙扩散系数模型得到的环线上固相速度定常结果对比。图15给出了小流量工况下，不同粒径时，3种泥沙扩散系数模型计算得到的各监测点上固相速度非定常结果对比。

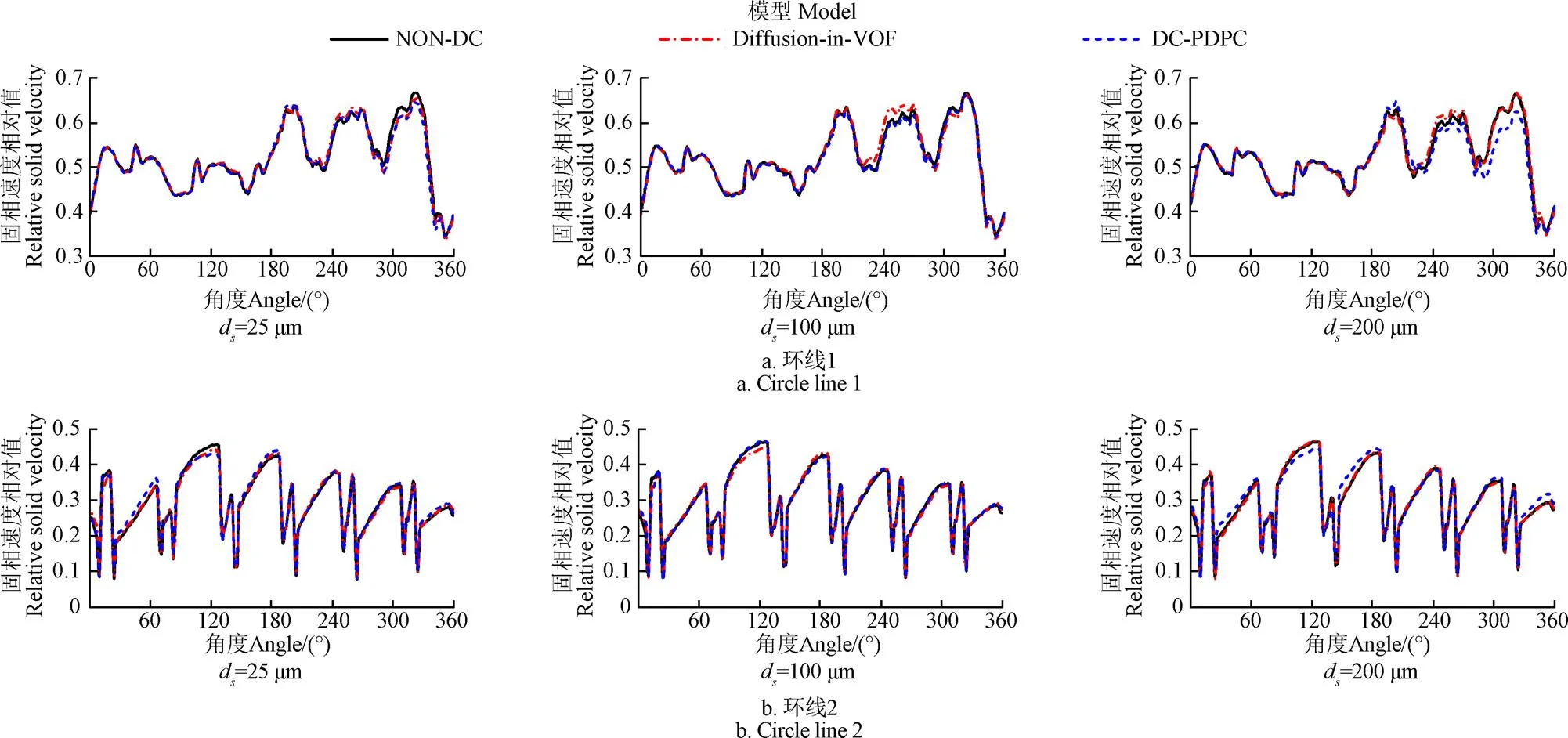
图14 小流量工况下不同粒径（ds）时不同泥沙扩散系数模型得到的环线上固相速度相对值定常结果对比

图15 小流量工况下，不同粒径（ds）时不同泥沙扩散系数模型得到的各监测点上固相速度相对值非定常结果对比

由图14可知，小流量工况下，3种泥沙扩散系数模型计算得到的叶轮内固相速度分布的定常结果在不同固相颗粒粒径时表现出不同的特性。当颗粒粒径分别为d=25 μm和d=100 μm时，同一颗粒粒径条件下，3种泥沙扩散系数模型计算得到的叶轮内固相速度分布整体分布较吻合，相差不大，相差最大为2%。当d=200 μm时，3种泥沙扩散系数模型计算得到的叶轮内固相速度分布的定常结果有所差异，但差异较小，相差最大为3%，整体上较吻合。这说明，小流量工况下，不同的泥沙扩散系数模型计算得到的双吸离心泵内固液两相流的固相速度分布的定常结果整体上差异不大，基本相同。小流量工况时，不同泥沙扩散系数模型对双吸离心泵内固相速度分布的定常结果影响不大。

由图15可知，小流量工况下，在同一固相颗粒粒径时，3种泥沙扩散系数模型在不同监测点上计算得到的固相速度的非定常结果差别较大，而且随着颗粒粒径的增大，3种泥沙扩散系数模型得到的固相速度非定常结果的差别逐渐增大，相差最大可达8%。这说明，小流量工况下，不同的泥沙扩散系数模型对双吸离心泵内固液两相流的固相速度分布的非定常计算结果影响较大；而且随着颗粒粒径的增大，3种泥沙扩散系数模型得到的固相速度分布非定常结果的差异逐渐增大。

综上所述，小流量工况下，不同的泥沙扩散系数模型计算得到的双吸离心泵内固液两相流的固相浓度分布的定常结果在小粒径颗粒时差别不大，随着颗粒粒径的增大，差异逐渐增大。因此，不同泥沙扩散系数模型对小粒径颗粒的固液两相流定常结果影响不大，NON-DC模型结构简单，推荐使用；但对大粒径颗粒的结果影响较大。

小流量工况下，不同的泥沙扩散系数模型对双吸离心泵内固液两相流的非定常计算结果影响较大；而且随着颗粒粒径的增大，不同泥沙扩散系数模型得到的非定常结果的差异逐渐增大，推荐使用DC-PDPC模型，该模型考虑了颗粒粒径对固相浓度的影响。

5 结 论

为了研究不同泥沙扩散系数模型用于双吸离心泵内固液两相流数值计算时对结果的影响，采用3种泥沙扩散系数模型对不同颗粒粒径时，不同工况下，双吸离心泵内的固液两相流进行定常和非定常数值计算。得到的主要结论为：

1）1.0Q（Q为额定流量，m3/s）工况下，在不同粒径颗粒条件下，不同的泥沙扩散系数模型计算得到的双吸离心泵内固液两相流的定常计算结果均基本相同，泥沙扩散系数模型对固液两相流的定常计算结果影响不大；但是，固相浓度分布非定常结果差异较大，而且随着颗粒粒径的增大，差异逐渐增大，固相浓度计算值相差最大达1.5%。

2）0.6Q工况下，不同的泥沙扩散系数模型计算得到的双吸离心泵内固液两相流的固相浓度分布的定常结果在小粒径颗粒（不大于100 μm）时，差别不大，随着颗粒粒径的增大，差异逐渐增大，固相浓度计算值相差最大可达60%。因此，不同泥沙扩散系数模型对小粒径颗粒（不大于100 μm）时的固液两相流定常结果影响不大，但对大粒径颗粒（大于100 μm）的结果影响较大。

3）0.6Q工况下，不同的泥沙扩散系数模型得到的双吸离心泵内固液两相流的非定常计算结果差异较大；而且随着颗粒粒径的增大，差异逐渐增大，固相浓度和速度计算值相差最大可达30%。

4）整体上来说，将3种泥沙扩散系数模型用于双吸离心泵内固液两相流数值计算时，当颗粒粒径不大于100 μm时，3种泥沙扩散系数模型得到的固液两相流场定常结果基本相同；当颗粒粒径大于100 μm时，定常结果有所差异，而且随着颗粒粒径的增大，差异逐渐增大。而对于不同颗粒粒径的条件，3种泥沙扩散系数模型得到的固液两相流场非定常结果均差异较大，而且随着颗粒粒径的增大，差异逐渐增大。

5）针对含沙颗粒粒径不大于100 μm时的定常计算，3种模型得到的结果基本相同，推荐NON-DC模型；随着颗粒粒径的增大，推荐使用DC-PDPC模型，可以使计算结果更精确。当非定常计算时，推荐使用DC-PDPC模型。

[1] 王福军. 水泵与水泵站（第二版）[M]. 北京：中国农业出版社，2011.

[2] 王志高，陈星，何成连. 水泵磨蚀及减阻节能[M]. 北京：中国水利水电出版社，2013.

[3] 资丹，王本宏，王福军，等. 开机组合对泵站进水系统泥沙浓度分布的影响[J]. 农业工程学报，2022，38(7)：59-68. ZI Dan, WANG Benhong, WANG Fujun, et al. Influences of start-up pump units on the sediment concentration for the intake system of a pumping station[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(7): 59-68. (in Chinese with English abstract)

[4] 侯建邦. 影响尊村引黄提水泵站效益的原因及主要技改措施[J]. 中国农村水利水电，2002(6)：52-53.

[5] 刘贤娟. 黄河尊村灌区泥沙问题研究[J]. 广东水利电力职业技术学院学报，2007，5(3)：55-58.

LIU Xianjuan. Study on sediment problem of irrigation district of zuncun yellow river diversion project[J]. Journal of Guangdong Technical College of Water Resources and Electric Engineering, 2007, 5(3): 55-58. (in Chinese with English abstract)

[6] 钱忠东，王焱，郜元勇. 双吸式离心泵叶轮泥沙磨损数值模拟[J]. 水力发电学报，2012，31(3)：223-229.

QIAN Zhongdong, WANG Yan, GAO Yuanyong. Numerical simulation of sediment erosion in double-suctions centrifugal pump[J]. Journal of Hydroelectric Engineering, 2012, 31(3): 223-229. (in Chinese with English abstract)

[7] 王福军. 计算流体动力学分析[M]. 北京：清华大学出版社, 2004.

[8] 谈明高，张可可，吴贤芳，等. 泵内大颗粒固液两相流流动试验[J]. 农业工程学报，2021，37(8)：62-67.

TAN Minggao, ZHANG Keke, WU Xianfang, et al. Experimental study on large particle solid-liquid two-phase flow in a centrifugal pump[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(8):62-67. (in Chinese with English abstract)

[9] BELT L, COUSOT T. Semi-spiral casing and runner Navier-Stokes simulation for a refurbishment project[C]// Proceeding of the 19th IAHR Symposium on Hydraulic Machinery and Systems, Singapore, 1998: 258-267.

[10] BLANCO M. Numerical flow simulation in a centrifugal pump with impeller-volute interaction[C]. ASME 2000 Fluid Engineering Division Summer Meeting. Boston: ASME, 2000: 11-15.

[11] SHUKLA S N, KSHIRSAGAR J T. Numerical experiments on a centrifugal pump[J]. American Society of Mechanical Engineers-Fluids Engineering Division, 2002, 257(2B): 709-720.

[12] TU J T, FLETCHER C A. An improved model for particulate turbulence modulation in confined two phase flows[J]. International Communications in Heat and Mass Transfer, 1994, 21(6): 775-783.

[13] 唐学林，余欣，任松长，等. 固-液两相流体动力学及其在水力机械中的应用[M]. 郑州：黄河水利出版社，2006.

[14] ESMAILI E, MAHINPEY N. Adjustment of drag coefficient correlations in three dimensional CFD simulation of gas-solid bubbling fluidized bed[J]. Advances in Engineering Software, 2011, 42: 375-386.

[15] ASKARIPOUR H, DEHKORDI M. Simulation of 3D freely bubbling gas-solid fluidized beds using various drag models: TFM approach[J]. Chemical Engineering Research and Design, 2015, 100: 377-390.

[16] 汪家琼，蒋万明，孔繁余，等. 固液两相流离心泵内部流场数值模拟与磨损特性[J]. 农业机械学报，2013，44(11)： 53-60.

WANG Jiaqiong, JIANG Wanming, KONG Fanyu, et al. Numerical simulation of solid-liquid two-phase turbulent flow and wear characteristics of centrifugal pump[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(11): 53-60. (in Chinese with English abstract)

[17] 吕友军，董旭斌，张天宁. 曳力和湍流对超临界水流化床传热特性的影响[J]. 工程热物理学报，2014，35(12)： 2437-2441.

LÜ Youjun, DONG Xubin, ZHANG Tianning. Effects of the turbulence and drag force on heat transfer characteristics in supercritical water fluidized bed[J]. Journal of Engineering Thermophysics, 2014, 35(12): 2437-2441. (in Chinese with English abstract)

[18] 张自超，王福军，陈鑫，等. 低浓度固液两相流相间阻力修正模型研究[J]. 农业机械学报，2016，47(12)：92-98.

ZHANG Zichao, WANG Fujun, CHEN Xin, et al. Modified interphase drag model for diluted solid-liquid two-phase flow[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(12):92-98. (in Chinese with English abstract)

[19] 章梓雄，董曾南. 粘性流体力学[M]. 北京：清华大学出版社，1998.

[20] LIU H J, SATO S. Modeling sediment movement under sheetflow conditions using a two-phase flow approach[J]. Coastal Engineering Journal, 2005, 47(4):255-284.

[21] NADAOKA K, YAGI H. Single phase fluid modeling of sheet-flow toward the development of “numerical mobile bed”[J]. Coastal Engineering, ASCE, 1990(1): 2346-2359.

[22] DONG P, ZHANG K F. Two-phase flow modeling of sediment motions in oscillatory sheet flow[J]. Coastal Engineering, 1999, 36(2): 87-109.

[23] DONG P, ZHANG K F. Intense near-bed sediment motions in waves and currents[J]. Coastal Engineering, 2002, 45(2): 75-87.

[24] 傅旭东，王光谦. 低浓度固液两相流的颗粒相动理学模型[J]. 力学学报，2003，35(6)：650-659.

FU Xudong, WANG Guangqian. Kinetic model of particulate phase in dilute solid-liquid two-phase flows[J]. Acta Mechanica Sinica, 2003, 35(6): 650-659. (in Chinese with English abstract)

[25] FU X D, WANG G Q, SHAO X J. Vertical dispersion of fine and coarse sediments in turbulent open-channel flow[J]. Journal of Hydraulic Engineering, 2005, 131(10): 877-888.

[26] VAN R. Sediment transport, part Ⅱ: Suspended load transport[J]. Journal of Hydraulic Engineering, 1984, 110(11): 1626-1638.

[27] SOKOLICHIN A, EIGENBERGER G. Simulation of buoyancy driven bubbly flow: Established simplifications and open questions[J]. Fluid Mechanics and Transport Phenomena, 2004, 50(1): 24-45.

[28] 张自超，陈鑫，王福军，等. 考虑颗粒动态尺度影响的泥沙扩散系数模型建立及应用[J]. 农业工程学报，2016，32(22)：129-137.

ZHANG Zichao, CHEN Xin, WANG Fujun, et al. Sediment diffusion coefficient model used in Eulerian algorithm for solid-liquid two-phase flow[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2016, 32(22): 129-137. (in Chinese with English abstract)

[29] 倪晋仁，王光谦. 泥沙悬浮的特征长度和悬移质浓度垂线分布[J]. 水动力学研究与进展，1992，7(2)：167-175.

NI Jinren, WANG Guangqian. Characteristic length and vertical concentration distribution of suspended sediment[J]. Journal of Hydrodynamics, 1992, 7(2): 167-175. (in Chinese with English abstract)

[30] 谭泽宇，刘海江. 振荡流层移输沙条件下悬沙层泥沙扩散系数垂向分布特征研究[J]. 海洋工程，2019，37(4)：35-44.

TAN Zeyu, LIU Haijiang. Study of vertical distribution of sediment diffusion coefficient in suspended layer under oscillatory sheet flow condition[J]. The Ocean Engineering, 2019, 37(4): 35-44. (in Chinese with English abstract)

[31] ABDELALI T, MIRA S, ABDELLAH G. Sediment diffusion coefficient model for predicting the vertical distribution of suspended sediment concentration in uniform open-channel flows[J]. Arabian Journal of Geosciences, 2020, 13: 1169.

[32] DEBASISH P, KOELI G. Effect of particle concentration on sediment and turbulent diffusion coefficients in open-channel turbulent flow[J]. Environ Earth Science, 2016, 75: 1245.

[33] 刘涛，韩迅，邓振辰. 波浪条件下悬移质泥沙分布特性的数值模拟研究[J]. 科学技术创新，2023(2)：50-53.

LIU Tao, HAN Xun, DENG Zhenchen. Numerical simulation of suspended load distribution under wave conditions[J]. Science and Technology Innovation, 2023(2): 50-53. (in Chinese with English abstract)

[34] 左利钦，陆永军，朱昊. 波流边界层水沙运动数值模拟—Ⅲ.底部高含沙层模拟[J]. 水科学进展，2019，30(6)：810-822.

ZUO Liqin, LU Yongjun, ZHU Hao. Numerical simulation of flow-sediment dynamics in wave-current bottom boundary layer: Ⅲ: Simulation of high concentration near the bottom[J]. Advances in Water Science, 2019, 30(6): 810-822. (in Chinese with English abstract)

[35] 郭玉臣，石志洲，王庆业，等. 基于现场实验结果对倾倒泥沙扩散数值模型参数率定研究[J]. 海洋通报，2016，35(2)：170-177.

GUO Yuchen, SHI Zhizhou, WANG Qingye, et al. Parameter determination of the numerical model for dumping sediment transport based on the field experimental results[J]. Marine Science Bulletin, 2016, 35(2):170-177. (in Chinese with English abstract)

[36] 王福军. 流体机械旋转湍流计算模型研究进展[J]. 农业机械学报，2016，47(2)：1-14.

WANG Fujun. Research progress of computational model for rotating turbulent flow in fluid machinery[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(2): 1-14. (in Chinese with English abstract)

[37] LUO G, LI R X, ZHOU L X. Numerical simulation of gas-particle flows with different swirl numbers in a swirl burner[J]. Tsinghua Science and Technology, 2000, 5(1): 96-99.

[38] DURST F, MILOJEVIC D, SCHONUNG B. Eulerian and Lagrangian prediction of particulate two-phase flows: A numerical study[J]. Applied Mathenatical Modelling, 1984, 8(2): 101-115.

[39] 张自超，李延频，陈德新. 双吸离心泵叶轮内泥沙磨损非定常特性研究[J]. 农业机械学报，2022，53(4)：140-148，191.

ZHANG Zichao, LI Yanpin, CHEN Dexin. Investigation on unsteady erosion characteristics in impeller of double suction centrifugal pump[J]. Transactions of the Chinese Society for Agricultural Machinery, 2022, 53(4): 140-148, 191. (in Chinese with English abstract)

[40] 卢金玲，郭蕾，王李科，等. 半开叶轮离心泵叶顶间隙非定常流动特性研究[J]. 农业机械学报，2019，50(6)：163-172.

LU Jinling, GUO Lei, WANG Like, et al. Unsteady flow characteristics of tip clearance in semi-open impeller centrifugal pump[J]. Transactions of the Chinese Society for Agricultural Machinery, 2019, 50(6):163-172. (in Chinese with English abstract)

[41] 吴贤芳，冯进升，刘厚林，等. 单流道离心泵定常非定常性能预测及湍流模型工况适用性[J]. 农业工程学报，2017，33(增刊1)：85-91.

WU Xianfang, FENG Jinsheng, LIU Houlin, et al. Performance prediction of single-channel centrifugal pump with steady and unsteady calculation and working condition adaptability for turbulence model[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(Suppl.1):85-91. (in Chinese with English abstract)

[42] EKAMBARA K, SANDERS S, NANDAKUMAR K, et al. Hydrodynamic simulation of horizontal slurry pipeline flow using ANSYS-CFX[J]. Industrial & Engineering Chemistry Research, 2009, 48(17): 8159-8171.

Influences of three types of sediment diffusion coefficient model on the calculation of solid-liquid two-phase flow in double suction centrifugal pump

ZHANG Zichao, LI Yanpin※, ZHANG Lanjin, CHEN Dexin

(1450045; 2450045)

Euler-Euler models can be used to describe the fluid and particulate phase suitable for the two-phase flow in a double-suction centrifugal pump. The sediment diffusion coefficient is one of the most important moduli to express the interaction between the solid-liquid phases. There are the commonly-used three models of the semi-empirical sediment diffusion coefficient. In this study, the NON-DC, Diffusion-in-VOF, and DC-PDPC models were used separately to numerically simulate the solid-liquid two-phase flow field in the double suction centrifugal pump. A systematic analysis was also made to clarify the effects of the three models of sediment diffusion coefficient on the steady and unsteady solid phase concentration and velocity at different flow rates under three particle sizes of 25, 100, and 200 μm. The results show that there was a similar steady calculation of solid-liquid two-phase flow in the double-suction centrifugal pump using different models of sediment diffusion coefficient under different particle sizes and rated operating conditions. However, there was a greatly different unsteady distribution in the solid phase concentration using different models of sediment diffusion coefficient. Specifically, the difference increased gradually under low flow conditions with the increase of particle size. Different models of sediment diffusion coefficient shared little influence on the steady solid-liquid two-phase flow for the small diameter particle no more than 100 μm, but there was a great influence on the large diameter particle greater than 100 μm under low flow conditions. Meanwhile, the steady solid-liquid two-phase flow was basically the same, when the particle sizedwas less than or equal to 100 μm. Once the particle size was more than 100 μm, the difference of steady increased gradually with the increase of particle size. The greatly different unsteady solid-liquid two-phase flow field was found under the conditions of different particle sizes, where the difference increased gradually with the increase of particle size. Therefore, the basic same was observed for the steady calculation of solid-liquid two-phase flow with the small diameter particle no more than 100 μm. However, there was quite difference both between the steady calculation with a large diameter particle greater than 100 μm and the unsteady calculation under different sediment conditions. Therefore, it is necessary to optimize the suitable model of sediment diffusion coefficient for these conditions.

sediments; numerical analysis; models; double suction centrifugal pump; diffusion coefficient model; steady; unsteady

2022-11-30

2023-01-01

国家自然科学基金项目（51909094）；华北水利水电大学高层次人才科研启动项目（201705010）

张自超，博士，讲师，研究方向为流体机械两相流体动力学。Email：zhangzichaozzc@126.com

李延频，博士，教授，研究方向为流体机械优化设计。Email：liyanpin@ncwu.edu.cn

10.11975/j.issn.1002-6819.202211252

TH311; S224

A

1002-6819(2023)-07-0077-12

张自超，李延频，张兰金，等. 三种泥沙扩散系数模型对双吸离心泵内固液两相流流场计算的影响[J]. 农业工程学报，2023，39(7)：77-88. doi：10.11975/j.issn.1002-6819.202211252 http://www.tcsae.org

ZHANG Zichao, LI Yanpin, ZHANG Lanjin, et al. Influences of three types of sediment diffusion coefficient model on the calculation of solid-liquid two-phase flow in double suction centrifugal pump[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2023, 39(7): 77-88. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.202211252 http://www.tcsae.org