数字半球摄影法获取植被表观聚集指数（ACI）采样尺度效应研究

佟一冬，焦子锑，尹思阳，张小宁，崔磊，谢蕊，郭静，李思杰，朱子栋

1.北京师范大学 地理科学学部 遥感科学与工程研究院,北京 100875;

2.北京师范大学 遥感科学国家重点实验室,北京 100875

1 引言

自然条件下，叶片在植被冠层中的分布往往不是随机的，它会因空间、植被结构等约束表现为不同尺度上的聚集状态。植被聚集指数CI（Clumping Index）是一个重要的植被冠层结构参数，表征了植被冠层中叶片非随机分布的程度（阎广建 等，2016），可量化为有效叶面积指数LAIeff（effective Leaf Area Index）与真实叶面积指数LAItrue（true Leaf Area Index）之比（Nilson，1971；Chen 和Black，1991，1992；Chen 等，2003）。据此定义可知，当叶片随机分布时，CI 值等于1.0；当叶片聚集分布时，CI 值则小于1.0，且叶片越聚集，CI 值会越小。植被聚集效应会影响太阳辐射在冠层中的分布，从而影响植被的光合作用和植被生产力（Chen等，2003，2005）。此外，CI在降水截获，蒸散发等生态过程研究中都发挥着重要作用。目前，CI 已作为一些地表模型LSM（Land Surface Model）的输入参数，是陆表水文、气候以及生态模型中重要的输入参数之一（Chen 等，2003；Baldocchi 和Wilson，2001）。因此，植被聚集效应的研究对生态学、水文学、碳循环以及全球变化等研究领域有重要的研究意义。

CI 的地面测量为CI 遥感产品的验证提供重要的数据支撑。CI 的地面测量方法主要分为直接测量和间接测量两大类。直接测量方法通过测量LAIeff和LAItrue，按照定义直接获得CI，准确度高、可靠性强，因此常被用来验证间接测量法（Fang，2021）。但直接测量法通常对植物具有破坏性，且成本高昂，会耗费大量人力物力。间接测量方法通常借助光学仪器，如叶面积测量仪LAI−2200、DHP、跟踪辐射与冠层结构测量仪TRAC（Tracing Radiation of Canopy and Architecture）、多波段植被成像仪MVI（Multiband Vegetation Image）、多光谱冠层成像仪MCI（Multispectral Canopy Imager）等。应用光学仪器间接测量的方法，原理上基于Beer−Lambert 定律，描述冠层对光辐射的传输和截获。间接测量方法具有效率高、成本低，且对冠层无破坏性等优点，因而得到了更为广泛的应用。目前，基于间接测量仪器估算CI 的算法大体上分为3 种：Chen 和Cihlar（1995）最早提出以模拟随机分布状态的孔隙累计分布函数与实际孔隙测量值进行对比的方法，简称CC 法，并率先将其应用于TRAC 仪器的地面测量；Lang 和Xiang（1986）基于统计学原理提出了有限长度平均法，简称LX法，随后Van Gardingen 等（1999）将LX 法应用于半球图像上的每个天顶环中；Leblanc 等（2005）结合上述CC 和LX 两种方法，提出了CLX 方法，CLX方法针对上述两种方法存在的问题进行了修正，在一定程度上提高了CI 估算的准确度。但目前，应用地面间接测量方法定量估算CI 还存在一些问题，如：应用不同仪器结合不同估算方法得到的CI存在较大不一致性。Ryu 等（2010）基于5 种地面间接测量仪器（LAI−2000、TRAC、DHP、数字冠层摄影测量DCP（Digital Cover Photography）、穿越辐射系统TRS（Traversing Radiometer System）对草原生态系统CI 的地面测量实验中，发现5 种仪器得到的CI 结果存在较为显著的差异，并且由于各仪器观测形式和设定方法的不同，测量结果之间常常很难进行直接比较；Leblanc 等（2005）将CC、LX 和CLX 等3 种方法应用于29个北部森林实验点，结果显示，在各实验点应用3种方法获取的CI 值表现出明显差异。因此，为了更准确的估算LAI，Ryu 等（2010）以LAI−2000 为例提出植被表观聚集指数（ACI）的定义，Fang 等（2018a）随后将ACI的概念拓展至多种地面间接测量仪器。综上，不同仪器和方法的CI 地面测量结果的不一致性和不确定性在一定程度上会造成CI 遥感产品验证的难度，从而可能进一步影响定量遥感的后续应用。

在几种常用的间接测量方法中，DHP 方法通常被认为具有易操作、成本低、效率高等优点，被广泛应用于地面CI 测量（Ryu 等，2010；Fang等，2018b）。此外，DHP 法提供了比其他光学仪器更精确的冠层孔隙采样空间，它可以从各个天顶角和方位角中提取孔隙率，从而结合LX 方法可以基于更精细的尺度和方向测量植被的表观聚集程度（Garrigues 等，2008），从而获得多采样尺度下的ACI。即，ACI 会因所选取的角度采样尺度的不同而不同，这在一定程度上给地面CI 测量结果带来了较大不确定性及不一致性。因此，结合DHP 方法和LX 方法估算ACI 时，角度采样尺度和方向选取对地面CI 测量结果的影响不可忽视。近年来，众多学者应用DHP 方法做了许多实践，但研究人员在结合DHP 和LX 方法时，对于角度采样尺度的选取大多是随机的（Fang，2021）。如：Leblanc 等（2005）以北美白桦、欧洲山杨以及西伯利亚云杉为研究对象，在DHP 图像中选取9°作为天顶方向的角度采样尺度，即划分10个天顶环；Pisek 等（2011）以欧洲白桦、榛树和苏格兰松树为研究对象，分别选取2.5°和5°作为观测天顶角和方位角的采样尺度；Zou 等（2020）以华北落叶松为研究对象，选取5°作为观测天顶角和方位角的采样尺度；Demarez 等（2008）以行播种的玉米作物为研究对象，选取的观测天顶角和方位角的采样尺度分别为2.5×4°、5×8°和10×16°，并将其测量结果分别与直接测量方法的结果进行比较，认为最适合玉米作物的角度采样尺度为10×16°；Fang等（2018b）以行播种的大豆、玉米和高粱作物为研究对象，在天顶方向和方位方向上对3种农作物均选取2.5×2.5°的采样尺度；Fang 等（2014，2018a）以行播种的水稻作物为研究对象，选取天顶角和方位角采样尺度均为10°。这些研究为结合DHP 方法和LX 方法估算ACI 提供了重要数据、方法和文献参考。

目前，应用DHP 方法测量ACI 的角度采样尺度及方向性的研究受到越来越多的重视。Fang 采取DHP 方法在中国东北的稻田研究区开展地面测量实验，基于LX 估算法（Lang 和Xiang，1986）分别在4 个几何单元尺度上估算ACI（Fang 等，2018a）：最小特定方向单元Ω（θ，φ）、同心圆环单元Ω（θ）、方位扇环单元Ω（φ）和立体角单元Ω（ν）。结果表明，水稻田的ACI 在4 个采样几何单元上一般表现为Ωapp（θ，φ）<Ωapp（θ），Ωapp（φ）<Ωapp（ν），即，随着几何单元尺度的增大，叶片的随机性增大，ACI 增大。Gonsomo 等（2010）同样基于DHP 和LX 方法评估了DHP 图像角度采样分辨率对LAI 和ACI的估算影响。结果表明，角度采样尺度的大小会显著影响LAI 和ACI 的估算结果。此外，ACI 随方向变化的特性也已被研究学者所认识，ACI与观测天顶角和方位角密切相关。已有研究表明，北方针叶林、温带森林以及草地的ACI值随观测天顶角的增大而增大（Chen，1996；Kucharik等，1999；Leblanc 等，2005）；而对于行列播种的农作物而言，ACI 随方向的变化更为复杂（Fang，2021）。综上所述，应用DHP 和LX 方法估算ACI 时，角度采样尺度选取的不同会引起ACI 估算结果的不一致，因此，选取角度采样尺度是至关重要的步骤之一。目前，研究人员在应用DHP 和LX 方法估算ACI时，虽然认识到角度采样尺度的选取会在很大程度上影响估算结果，但是，针对角度采样尺度对ACI的影响规律，及其与不同植被类型的关系等问题仍有待进一步研究。

针对上述问题，本研究基于DHP 测量数据，在0°—90°的观测天顶方向（θ）和0°—360°观测方位方向（φ）上，围绕角度采样尺度展开，分别以一系列逐级增大的角度采样尺度∆θ和∆φ对DHP图像进行划分，共可得到30 种不同的DHP 图像采样方法；并将划分出的天顶环数与方位扇数的乘积定义为DHP 图像的角度采样分辨率，理论上便可得到30 个等级的角度采样分辨率，然而，由于存在天顶和方位两个不同的采样方向上的采样乘积结果对应同种角度采样分辨率的情况，因此，综合角度采样分辨率相等的情况后，共可得到17 个等级由高到低的角度采样分辨率。本文首先分别探究在观测天顶方向和方位方向上角度采样尺度∆θ和∆φ的递增对ACI 估算的影响，以及在17 个等级的角度采样分辨率下ACI 估算结果的变化规律；同时，分别以林、灌、草和农作物为研究对象，探究角度采样尺度的方向依赖性在四种不同植被类型下的表现；此外，将农作物的生长阶段、植被在空间中的分布形态以及DHP 的观测方向作为影响因素，进一步探究不同影响因素下，角度采样分辨率对ACI估算结果的影响。

本研究针对CI 地面测量通常所采用的方法展开研究，试图揭示ACI角度采样尺度效应的方向依赖性规律，并总结不同植被类型下角度采样尺度对ACI 估算结果影响的统一性和差异性，同时为CI 遥感产品验证的不确定性分析提供更为精细有效的地面测量数据分析支撑。

2 数 据

2.1 研究区和采样设计

本研究的地面实测数据来源于两个研究区。第一研究区位于河北省张家口市蔚县，地处张家口市境内最南端，太行山西北麓，地理坐标为39°34'N—40°10'N，114°13'E—115°04'E。面积约3220 km2，海拔高度在900—2880 m，属暖温带大陆性季风气候。此研究区地类以草地、林地为主，耕地为辅。其中，林地资源内包括松树、柏树、白桦、落叶松等树种；耕地内主要为白菜作物。第二研究区位于黑龙江省海伦市附近的农田区域，地理坐标为47°24'N，126°50'E。该地区属以东亚季风为主的寒温带大陆性气候，年平均气温为2 ℃，极端气温为−39.5—37 ℃（Liu 等，2013）。年平均降水量为500—600 mm，6—8 月降水率为60%—70%。该研究区以玉米和大豆等农作物为主。

在第一研究区内，综合考虑其地形、地类分布以及可到达性等特征，选取了地类相对均一、地形较为平坦的11 个500 m×500 m 的样方，在每个样方内，选取具有代表性的3—4 个30 m×30 m的基本采样单元ESU（Elementary Sampling Unit）。在每个ESU 内，利用配备好的数码相机和鱼眼镜头等设备，以6 m 为采样间隔，行列为采样单位，共获取25 张DHP 图像。在25 张DHP 图像中优先选取图像清晰、无遮挡物、无曝光且色调一致的8—12张图像，分别进行数据处理和CI估算。

在第二研究区内共选取2个相对平坦且均匀的样方，样方内为大豆作物，样方尺寸均大于100 m×500 m。作物南北朝向，整齐地按行播种，行间距约为0.63 m，作物密度约为24.6 株/m2。每个样方内选取3 个具有代表性的ESU，约为20 m×20 m，ESU 距农田边界距离至少为5 m。数据测量时间为2016 年6 月20 日至9 月22 日，每个星期对各个样方进行测量一次，测量时间覆盖大豆作物整个生长季。

2.2 数据获取

本研究选取CI 地面间接测量法中的DHP 方法。测量设备为Nikon D3500 数码相机，有效像素约为2416万；搭配SIGMA 4.5 mm F2.8 EX DC 半画幅鱼眼镜头，视角范围为180°，其采用SLD 低色散镜片，以达到出色的色差以及像差校正。拍摄时设定光圈优先，最大光圈F2.8，由相机自动设定最佳曝光时间，以避免测量时出现方向转换过程中不恰当的过度曝光。

在第一研究区中，当观测对象为草地时，相机置于冠层上方1.5 m 处保持水平下视观测；当观测对象为灌从时，相机置于地面正上方1 m处保持水平上视观测；当观测对象为森林时，相机置于1.7 m 处保持水平上视观测。在第二研究区中，当大豆作物高度<30 cm 时，相机置于距离其表面以上至少50 cm 处下视观测；当大豆作物高度>30 cm时，相机置于距地面<30 cm 处上视观测。所有图像保存为分辨率为6000×4000个像元的JPEG 格式。本研究所有观测均在接近日落或阴天条件下进行，以尽量减小太阳直射下可能产生的观测误差。

2.3 数据预处理

DHP 图像的预处理包括蓝光波段提取、有效成像区域提取和图像分类3 个主要步骤。研究表明，叶绿素对光谱中的蓝光波段具有更低的反射率和透射率，因此，叶子在蓝光波段中的表现相较红光和绿光波段而言更暗（Leblanc 等，2005），故首先在彩色图像中提取出蓝光波段。其次，在整幅DHP 图像上提取有效成像区域是进一步提取冠层结构参数的前提。本研究采取扫描线逼近法提取有效成像区域，即在设定好一个经验阈值条件下，图像上、下、左、右4条扫描线向中心逐行逼近，根据极限亮度差阈值，逐渐构成有效成像区域的外接正方形，以此正方形来计算有效圆形成像区域的圆心坐标及半径值。在理想情况下，在扫描线停止扫描后，4 条边界所围成的矩形区域为正方形，但由于采集设备不可避免会出现某些特殊情况，可能会导致最终结果出现微小偏差。若出现偏差，选取两个半径值中的较小值。其中，经验亮度阈值的设定，依据实际相机和设备的实际情况可以灵活选取（宋佳音，2017）。本研究根据多个场景实测图像的测试结果显示，选取经验亮度阈值为70 时提取结果较好，故选取经验阈值为70。如图1 所示为第一研究区林、灌、草的DHP实测数据。

图1 林、灌、草地面ACI实测数据Fig.1 Three scenarios regarding ACI field measurement of fores，shrub and grass

DHP 图像预处理的最后一步为图像分类，即将图像中的植被像元与天空（土壤）像元划分为两类。本研究针对上视和下视图像采取不同的图像分类方法。在上视图像中，植被像元与天空像元的灰度值差异明显，因此，采取直方图选取阈值法对图像进行二值化处理。所选阈值为输出直方图中植被像元波峰与天空像元波峰间波谷的最低值；在下视图像中，由于植被像元与土壤像元灰度值相似会导致较大的分类误差，因此，在ENVI 软件中选择基于感兴趣区域的支持向量机分类法SVM（Support Vector Machine），将植被与土壤分离有效分离。

3 方 法

3.1 Lang 和 Xiang CI估算方法

聚集效应最初由NILSON 在1971 年首次提出并定义，该定义使用参数Ω描述了非随机叶片空间分布对植被冠层辐射传输的影响（Nilson，1971）：

式中，P（θ）为观测天顶角θ下的孔隙率；G（θ）为叶片投影函数，对于叶倾角随机分布的植被冠层，通常取0.5；LAIeff为有效LAI，LAItrue为真实LAI。植被冠层结构中的聚集现象会造成叶子比随机分布状态下在垂直或其他方向上更多的重叠，因此增加了辐射透过冠层的可能性，CI 和LAI 的乘积有效地决定了通过冠层的辐射传输（LAIeff=LAItrue× CI）。

Miller提出了一个无需G(θ)先验知识的方法来估算LAIeff（Miller，1967）：

Ryu首次定义由式（3）与式（4）之比为植被表观聚集指数（Ωapp）（Ryu等，2010）：

式（5）通过测量的LAIeff与近似的LAItrue之比遵循了Ω一直以来的定义（Leblanc 等，2005；van Gardingen 等，1999）。同时，式（5）为Lang 和Xiang 基于统计学原理提出的有限长度平均法的基本形式，简称LX 法（Lang 和Xiang，1986），可简单表示为

式中，θ为观测天顶角；P(θ)为θ下有限长度子样线内的孔隙率。当存在多个观测天顶角时，需对各天顶角下的孔隙率求取平均值。式中，分子为对各有限长度子样线上孔隙率的平均值求对数，分母为对各个有限长度子样线上孔隙率的对数求平均值。

Lang 和Xiang（1986）的研究表明，在聚集冠层有限长度的子样线上求对数平均法可以获取更准确的估算结果。但此方法存在两个前提假设：（1）在有限长度的子样线内，叶片近似随机分布；（2）有限长度子样线内存在孔隙，即孔隙率不为0，因为0 的对数在数学上无意义。因此，应用此方法时，选取的子样线大小应该足够小，满足假设（1）；同时，子样线大小应该足够大，使孔隙率的统计有意义，满足假设（2）。已有研究表明，所选取的子样线的大小会在极大程度上影响ACI的估算结果（Gonsamo 等，2010）。因此，选取适当的子样线的大小是至关重要的，而选取能够同时满足两个假设的子样线的大小是较为困难的。目前，针对子样线的大小对ACI的影响规律，以及如何选取适用于不同植被类型的子样线大小等问题仍待解决。因此，为了满足上述两个前提假设，在更宽范围的采样尺度上探究上述问题，本研究基于DHP 图像，提出以一系列角度采样尺度分别对观测天顶角和观测方位角划分，而后将两个方向上的角度采样尺度依次一一结合，便可得到对于整幅图像30 种不同的子样线划分方法，即采样方法。基于30 种不同子样线应用LX 方法估算ACI，从而可以进一步分析ACI 估算结果的统一性和差异性。详见3.2节所述。

3.2 角度采样分辨率划分

基于DHP 观测数据，应用LX 方法进行ACI 估算时，上述子样线的大小由两个要素共同决定：观测天顶角采样尺度∆θ和观测方位角采样尺度∆φ（如 图2（a）所 示∆θ=∆φ=5°、（b）所 示∆θ=∆φ=15°）。以一定的∆θ对0°—90°的观测天顶角划分，可得到天顶圆环N=90°/∆θ个；以一定的∆φ对0°—360°观测方位角划分，可得到方位扇环M=360°/∆φ个。

图2 子样线大小划分Fig.2 Sampling segment divided

本研究在0°—90°的观测天顶角上制定∆θ=5°、6°、7.5°、10°和15°共5 个角度采样尺度，其对应的天顶圆环个数（N）分别为12、10、8、6、4（如图3（a）、（b）所示）；在0°—360°的观测方位角上制定∆φ=5°、6°、7.5°、10°、12°和15°共6 个角度采样尺度，其对应的方位扇数（M）分别为72、60、48、36、30、24（如图3（c）、（d）所示）。基于DHP 图像，将观测天顶方向上的5 个采样尺度与观测方位方向上的6个采样尺度依次一一结合，便可得到对于整幅图像的30 种不同的子样线划分方法。根据式（6）可知，不同的子样线划分方法决定了孔隙率的大小，而孔隙率的大小决定了ACI的估算值（ΩLX），因此，通过上述一系列采样单元的划分，共可得到在30 种大小不同的子样线下ACI的估算结果及其统一性和差异性。

图3 DHP图像角度采样分辨率划分案例，观测天顶角定义为θ，观测方位角定义为φFig.3 Examples of the angular sampling resolution division of DHP in terms of view zenith angle（VZA，θ）and view azimuth angle（VAA，φ）

在本研究中，定义天顶圆环数（N）与方位扇环数（M）的乘积为DHP 图像的角度采样分辨率（R）（式（7）），据此，将上述观测天顶方向上划分得到的5个等级的N与观测方位方向上划分得到的6个等级的M一一相乘后，理论上共可得到DHP图像30 个等级的R。然而，由于以不同的∆θ和∆φ划分子样线时，其对应的N和M在相乘后可能会得到相同的R，例如，分别以∆θ=5°（N=12）、∆φ=6°（M=60）和∆θ=6°（N=10）、∆φ=5°（M=72）划分子样线后，得到的R均为720。因此，综合R值相等的情况后，共可得到17 个等级由高到底的R（表1）。通过分析ACI 在17 个等级的R上的变化，可以进一步探究ACI随角度采样尺度逐渐增大的变化规律。

表1 角度采样分辨率划分Table 1 Angular Sampling Resolution Division

3.3 孔隙率提取

由式（6）可知，获取冠层孔隙率P(θ)是计算ΩLX的基础。孔隙率为任意特定位置投影到像平面内天空（土壤）组分像元占单元内总像元数量之比。在数据预处理阶段已将DHP 图像进行二值化处理，将图像内像元划分为天空（土壤）组分和植被组分两大类，以W（S）代表天空（土壤）组分，像素值为1（0），B代表植被组分，像素值为0（1）。

按照3.2 节中以不同尺度等级划分子样线的方法，对二值化后的DHP 图像进行子样线划分。划分后得到若干子样线单元，单元个数与其角度采样分辨率相对应。在每一个单元内，Pw(s)为天空（土壤）组分出现的个数，PB为植被组分出现的个数，则每一个单元的孔隙率可由下式计算：

利用式（8）可以提取0°—90°观测天顶角和0°—360°观测方位角范围内的孔隙率。

当子样线单元内不存在孔隙时需要进行修正。目前主要有两种修正方法（Walter 等，2003），一种应用广泛的方法是由Van Gardingen 等（1999）提出，当子样线内孔隙为0时，为其分配一个像元的孔隙，使其可以正常进行对数运算，并依据先验知识赋予此子样线的孔隙率一个边界值；另一种方法是忽略无孔隙的子样线（Walter等，2003）。而实际上，无孔隙的子样线区域叶片密集，若直接删除必然会带来较大估算误差。本研究选择Van Gardingen 等（1999）的方法作为处理无孔隙子样线的备用算法。

4 结果与分析

4.1 林、灌、草ACI测量的变化规律

根据3.2 节所述，分别以5 个等级的∆θ和6 个等级的∆φ对观测天顶角和观测方位角划分，每次控制一个方向的角度采样尺度不变，另一个方向的角度采样尺度依次增大。如图4所示为在林、灌、草3种地类下，ACI分别随观测天顶角（VZA）、观测方位角（VAA）采样尺度增大的变化规律。

图4 3种地类下VZA、VAA采样尺度对ACI估算影响Fig.4 The influence of VZA、VAA sampling interval scale on ACI estimation of three types of vegetation

从整体上来看，3种地类下ACI随VZA 和VAA采样尺度的增大均呈现增大趋势。其中，随VAA采样尺度的增大，ACI整体趋于线性增长，并且在各采样尺度间增长幅度较小，均匀平缓；而随VZA采样尺度的增大，ACI在各采样尺度间增长幅度较大，但整体也呈现出线性增长趋势。此外，随VZA 采样尺度的增大，ACI 始终保持正增长；而随VAA 采样尺度的增大，ACI 在大部分采样尺度中均呈现正增长，但在林地和草地两种地类中，ACI 在VAA 采样尺度由10°增长至12°的过程中出现下降趋势。经定量分析，在林、灌、草3种地类下，ACI 在VZA 采样尺度由5°增大至15°的过程中，总体平均增幅分别为15.8%、16%和7.92%；ACI 在VAA 采样尺度由5°增大至15°过程中，总体平均增幅分别为10%、11.5%和5.25%。

以灌丛为例，图5（b）—（f）为VAA 采样尺度保持5°不变的情况下，VZA 采样尺度分别为5°、6°、7.5°、10°和15°时，ACI 的彩色环状图。图5更形象地展示了在0°—60°观测天顶方向上VZA 采样尺度增大时，每个天顶环内ACI值的变化及其变化的整体趋势。

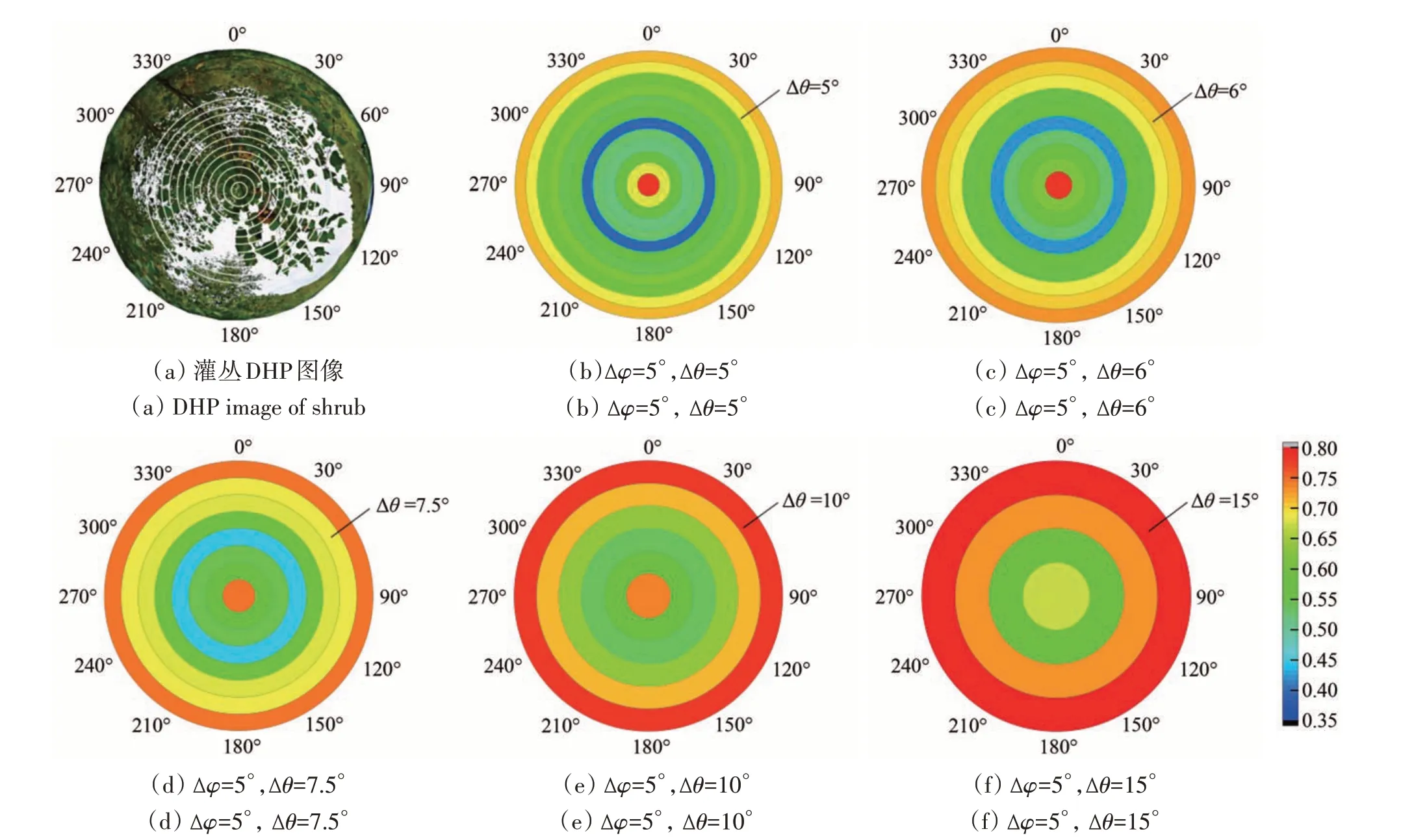
图5 VZA采样尺度对ACI估算影响。以灌丛为例，展示各天顶环内ACI的变化情况；其中（b）—（f）中VZA采样尺度分别为5°、6°、7.5°、10°和15°；VAA采样尺度保持5°不变Fig.5 The influence of VZA sampling interval on ACI estimation.Taking shrubs for example，the ACI changes in each zenith ring were shown；the sampling scale of VZA in（b）—（f）were 5°、6°、7.5°、10° and 15°，respectively；the VAA sampling scale remains unchanged at 5°

总括上述分析，我们可以看出，观测天顶方向和观测方位方向上采样尺度的变化对ACI估算值均有一定的影响，影响值最大可达16%，最小达5.25%。其中，相较观测方位方向，ACI 对观测天顶方向上采样尺度的变化更为敏感。

如图6 所示为在30 种不同子样线、17 个等级的角度采样分辨率下ACI值的增长情况。从整体上来看，林、灌、草3种地类下，随角度采样分辨率的降低，ACI 均表现出较好的线性增长趋势，ACI总体变化幅度分别为［0.53，0.67］，［0.55，0.70］和［0.74，0.84］，平均增幅分别达到26%、27.5%和13.5%。其中，灌丛地类下ACI 增长的线性趋势优于林地和草地，对其进行线性回归分析，3 种地类的R2分别为0.92、0.973 和0.956。在灌丛地类下，ACI随角度采样分辨率的降低而增大的线性趋势和涨幅均最为显著；相对于草地来说，林地ACI随角度采样分辨率的降低而增大的涨幅也较为显著。

图6 林、灌、草地类下角度采样分辨率对ACI估算影响Fig.6 The influence of angular sampling resolution on ACI estimation for forest，shrub and grass

在角度采样分辨率降低的过程中，ACI总体呈线性趋势，但其线性拟合程度与特定分辨率下对应的多个ACI值之间的离散程度有关。即由于角度采样分辨率同时受VZA 和VAA 双向决定，因此在角度采样分辨率相同时，可以划分出不同子样线的情况，而不同的子样线对应着多个ACI 值。如表1 中下划线处所示，当角度采样分辨率为288 时，对应的4 种子样线划分标准分别为∆θ=5°，∆φ=15°；∆θ=15°，∆φ=5°；∆θ=7.5°，∆φ=10°；∆θ=10°，∆φ=7.5°，即同一角度采样分辨率可以最多对应4 个ACI 值（0.618，0.622，0.629，0.647，即，图6 中的垂直虚线所示）。由图6 所示，相较林地和草地而言，灌丛地类中在同等角度采样分辨率下，ACI 值对于划分子样线方式的敏感度较低，因此线性趋势的拟合程度较高；但其对于角度采样尺度增大的敏感度较高，因此总体涨幅最为显著。

此外，如前文所述，3 种地类下，ACI 在VZA采样尺度由5°增大至15°的过程中，总体平均增幅分别为15.8%、16%和7.92%；在VAA 采样尺度由5°增大至15°过程中，总体平均增幅为10%、11.5%和5.25%；而随角度采样分辨率的降低，ACI 总体平均增幅分别达到约26%、27.5%和13.5%。即，各地类在角度采样分辨率逐级降低的过程中，ACI总体平均增幅为ACI分别在观测天顶方向总平均增幅与观测方位方向总平均增幅之和。由此再次证明，由于DHP 图像的角度采样分辨率是由观测天顶和观测方位两个方向上的角度采样尺度构成的，因此，角度采样分辨率对ACI的影响会综合两个方向上角度采样尺度对ACI造成的影响，从而导致在应用LX 方法时，角度采样分辨率的选取对ACI 产生加倍的影响。

4.2 行播作物大豆的ACI测量的变化规律

4.2.1 下视观测

如图7（a）—（c）所示为2016 年6 月26 日（DOY 178）、7 月3 日（DOY 185）、7 月8 日（DOY 190）分别在同一样方、同一ESU 内，大豆作物在3个生长阶段下视拍摄的DHP图像。

图7 下视大豆作物DHP图像数据Fig.7 The DHP images of downward observation of soybean crops

从DHP图像来看，3个生长阶段的差异主要在于垄间距离的逐渐减小和叶片数量的增多与浓密，使大豆冠层逐渐从行播垄状作物成长为连续植被。在生长初期（图7（a）），叶片较为稀疏，垄间距离较大，视场角内的垄沟清晰可见；随着大豆生长状态趋于旺盛（图7（b）），叶片逐渐繁茂，视场角内垄间距离明显减小，垄沟若隐若现；在大豆生长到极其繁茂阶段（图7（c）），叶片几乎覆盖了原本的垄沟，视场角内垄间距离几乎只剩缝隙。

分别对3 个生长阶段的DHP 图像应用LX 方法进行ACI 估算，如图8（a）—（c）所示，分别为在大豆作物3 个生长阶段下，ACI 随VZA、VAA 采样尺度增大的变化规律。

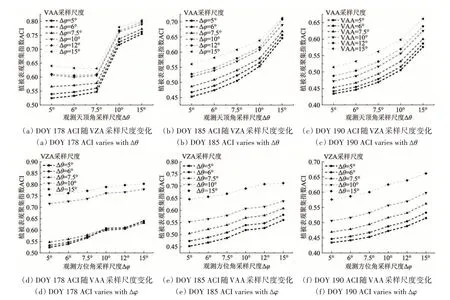
图8 DHP下视：VZA、VAA尺度对ACI估算影响Fig.8 The influence of VZA and VAA interval on ACI estimation for DHP downward observation

从整体上来看，3 个生长阶段下ACI 随VZA 和VAA采样尺度的增大均呈现增大趋势。其中，ACI随VAA 采样尺度的增大整体仍趋于线性增长，并且在VAA各采样尺度间增长幅度较小，与林、灌、草3 种地类基本一致；而随VZA 采样尺度的增大，ACI 在生长初期阶段表现出了明显的阶跃增长（图8（a）），与之后的生长阶段有显著差异，这与林、灌、草3种地类也有明显不同。

在3 个生长阶段下，ACI在VZA 采样尺度由5°增大至15°过程中，平均增幅分别为34.59%、35.79%和31.61%；ACI 在VAA 采样尺度由5°增大至15°过程中，总体平均增幅分别为14.2%、18.5%和18.14%。由此可见，对于下视大豆作物而言，ACI 在VZA 和VAA 两个方向上随采样尺度增大的平均增幅明显高于林、灌、草地类下的平均增幅。

从总体上来看，观测天顶方向和观测方位方向上角度采样尺度的变化对ACI估算值均有一定的影响，影响最大值可达35.79%，最小值达14.2%。其中，观测天顶方向上的影响尤为显著，且和垄状作物的行播方式有关。

如图9（a）—（c）所示，为在30 种不同子样线、17 个等级的角度采样分辨率下ACI 值的增长情况。从整体上来看，在大豆作物生长的3个阶段下，随角度采样分辨率的降低，ACI的表现大不相同，与林、灌、草3 种地类下的表现也有很大差异。首先，可以明显看出，在大豆生长初期和中期，ACI随角度采样分辨率的降低呈现明显的分层阶跃现象，并且分层前后都呈现出线性趋势；在生长茂盛阶段，这种分层程度大大减小，ACI整体趋于线性增长趋势。

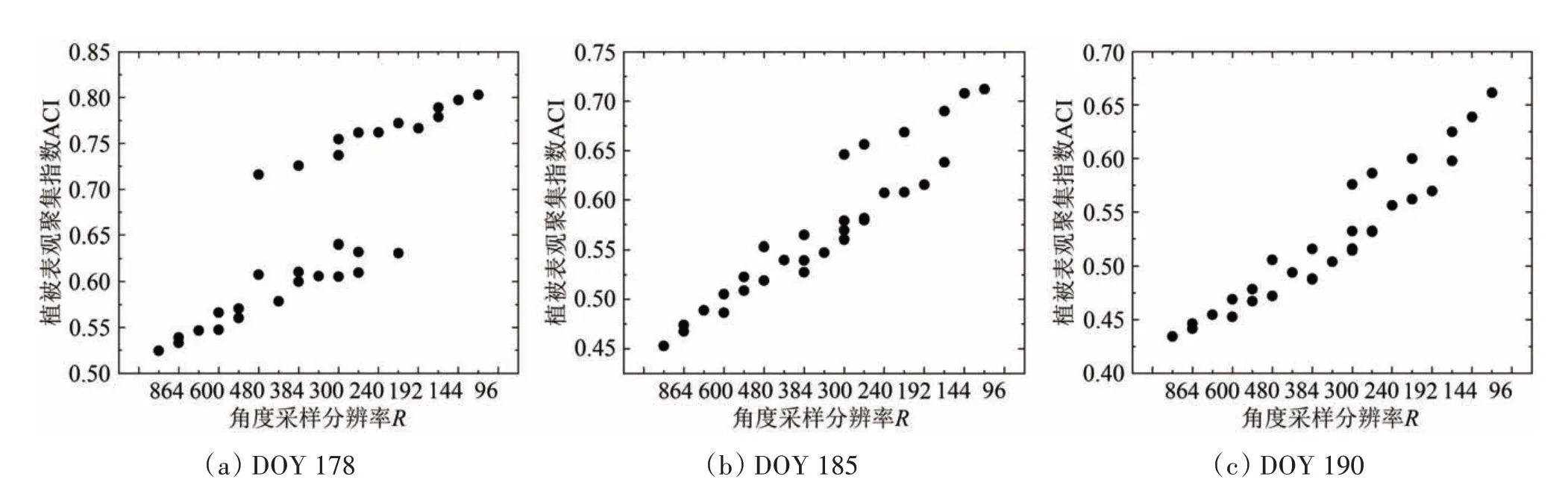
图9 农作物类型下角度采样分辨率对ACI估算影响Fig.9 The influence of angular sampling resolution on ACI estimation for crop

结合大豆作物在3 个阶段下的DHP 图像（图7）、观测天顶方向上角度采样尺度的增大对ACI 的影响（图8（a）），以及角度采样分辨率降低对ACI 的影响（图9（a）），可以判断，产生此种阶跃现象的原因是行播作物在生长过程中，不同生长阶段垄间距离不断减小导致的。即阶跃现象随垄间距离的增大而显著，随垄间距离的减小而逐渐消失。这种阶跃现象在林、灌、草3种地类下均未表现，而在行播作物中才有所表现，这清楚表明垄状作物的行播方式对ACI测量结果影响明显，且随作物生长过程的生长状态而变化。由此说明，ACI随角度采样分辨率降低的变化与植被冠层的空间分布形态密切相关。

4.2.2 上视观测

为了进一步探索垄状结构对ACI测量结果的影响，本研究选取了行播大豆的9个生长节点，采用上视观测方式进行研究，如图10（a）—（i）所示。自2016 年7 月16 日 起（DOY 198）至9 月16 日（DOY 260），以6 天为间隔，在同一样方、同一ESU 内，上视拍摄了大豆作物的DHP 图像，包含了大豆作物从幼苗生长末期、花芽分化期、开花结荚期、鼓粒期直至成熟期的各生长阶段。

图10 大豆作物生长节点Fig.10 The growth process of soybean crop

从DHP 图像来看，大豆在上述生长阶段的差异主要在于叶片数量的变化、垄间距离的变化以及叶片空间分布形态的变化。在幼苗生长末期（DOY 198，图10（a）），叶片生长状态尚未达到繁茂阶段，叶片明显地分布在左右两列，垄间距离较为清晰，但与下视观测的3 个阶段（DOY 178、185、190）相比，已更接近封垄状态；随着生长逐渐旺盛，作物开始进入花芽分化期（DOY 204、213、220，图10（b）—（d）），叶片数量明显增加，直至达到顶峰，垄间间隙逐渐收缩，叶片几乎覆盖了整个视场；随后，作物开始进入开花结荚期和鼓粒期（DOY 226、239、248，图10（e）—（g）），视场内的叶片分布形态开始出现转变，视场内的大孔隙转化为更多的小孔隙，叶片在前一阶段的两列分布形态逐渐消失，叶片数量也开始呈现负增长；最后，大豆进入成熟期（DOY 254、260，图10（h）—（i）），叶片大量凋落枯萎，大孔隙再次出现。

分别对上述各生长阶段的DHP 图像应用LX 方法进行ACI 估算，如图11（a）—（i）所示，为30 种不同子样线、17 个等级角度采样分辨率下ACI值的大小增长情况。在大豆作物由幼苗生长末期至成熟期的系列生长阶段中，ACI随角度采样分辨率的降低表现出了较为复杂的变化规律。

图11 角度采样分辨率对ACI估算影响Fig.11 The influence of angular sampling resolution on ACI estimation

从整体上看，在大豆作物上述9 个生长节点下，ACI随角度采样分辨率的降低由开始较为发散的指数增长趋势（图11（a）—（b）），逐渐转换为愈发清晰的指数增长趋势（图11（c）—（d））；而后又由指数增长趋势逐渐转化为显著的线性增长趋势（图11（e）—（g））；最后，由显著的线性增长趋势逐渐转化为拟合程度和斜率降低的线性增长趋势（图11（h）—（i））。其中，由指数增长趋势转换为线性增长趋势的过程中，发挥起承转合作用的生长节点为图11（e）所示，即完成封垄状态后，叶片在视场内分布形态开始发生变化的生长阶段。此后，直到作物开始进入到成熟期阶段，视场内大孔隙的再次出现，ACI随角度采样分辨率降低的线性增长趋势再次开始转变。由此再次证明，ACI随角度采样分辨率降低的表现与植被冠层的空间分布形态密切相关，而对于农作物来说，植被冠层的空间分布形态与作物的生长阶段密切相关。

5 结论

ACI与角度采样尺度密切相关，同时也与观测方向密切相关，角度采样尺度和方向选取的不同均会引起ACI 估算结果的不一致。近年来，DHP间接测量法应用较为广泛，将其与LX 方法结合起来，可以基于更精细的尺度和方向估算ACI。然而，在地面测量中，由于角度采样尺度和方向选取的不同给CI测量结果带来的影响可能是巨大的。因此，为保证地面CI 测量结果的一致性，结合此两种方法时的关键步骤之一即是选取角度采样分辨率。而DHP 图像的角度采样分辨率是由角度采样尺度和采样方向共同决定的，因此，本文以探究ACI对角度采样尺度和方向的依赖性，以及所选取的角度采样分辨率对ACI 估算结果的影响为目的，从而系统展开了ACI采样尺度效应的研究。

本研究以林、灌、草和大豆作物4种地类作为研究对象，选取DHP 间接测量法，应用LX 估算ACI 法，基于ACI 的方向性变化，进一步探究了ACI随角度采样尺度的变化在方向上的依赖性。同时，以非规则分布与规则分布的场景为观测对象，结合DHP 上视与下视两种观测方向，分析了（1）在林、灌、草3 种非规则分布的地类下，ACI随角度采样尺度的变化与观测天顶方向和观测方位方向的依赖关系，以及ACI随总体角度采样分辨率变化的变化规律；（2）大豆作物在不同的生长阶段，ACI随角度采样分辨率变化而变化的规律与观测对象空间分布形态的关系。

研究结果表明，ACI随角度采样尺度的变化具有方向依赖性，并且这种特性会受到观测对象空间分布形态的影响。当观测对象为非规则分布时（林、灌、草地类），随VZA和VAA采样尺度增大，ACI总体表现出线性增长趋势，增长趋势可能会受植被类型影响略有不同；当观测对象为规则分布时（大豆作物），ACI 仍受VZA 和VAA 采样尺度的影响，其中VZA 采样尺度对ACI 影响非常显著。经分析发现，引起这种显著影响的原因主要在于行播规则分布的场景中行播间隔的影响，即，在行播作物生长过程中，行播间隔越明显，ACI随VZA采样尺度的增大则会产生越显著的阶跃式增长。此外，大豆作物在一系列生长阶段中，ACI随角度采样分辨率的降低依次表现出了由指数增长转化为线性增长，再由线性增长转化为趋于分层增长的复杂变化。经分析认为，这种复杂的变化与行播作物生长过程中在空间中的分布形态有关。针对这一复杂变化产生的原因，后续还需进一步探究。

综上所述，本研究结果表明，ACI会随着角度采样尺度的增大而增大，即随着角度采样尺度增大，植被聚集程度减弱，逐渐趋于随机分布。这一研究结果在一定程度上与Fang（2018a）、Gonsamo等（2010）的研究结果相符合。此外，本研究在此基础上展开了进一步探索，揭示了ACI对角度采样尺度变化而变化的方向依赖性，以及在不同植被类型下，角度采样尺度对ACI估算结果影响的统一性和差异性。综上，在实地中应用DHP法结合LX 方法进行CI地面测量时，应考虑角度采样尺度对CI 的影响，本文的研究结果可以为CI 地面测量的不确定性提供一定的范围参考。此外，针对不同植被类型，如何选取最优角度采样尺度的问题将是下一步研究的重点。

对ACI地面测量进行精细分析，以及测量过程中可能存在的不确定性问题的深入探讨是展开CI遥感产品真实性检验的前提研究，对于提高CI 估算精度和CI 产品验证精度均具有一定意义，因此这也是目前遥感地表关键参数测量和反演研究的一个重要方向。

志 谢此次野外实验的数据获取得到了中国科学院地理科学与资源研究所资源环境信息系统国家重点实验室的支持，在此表示衷心的感谢！（http：//www.lreis.ac.cn/kfjl/zlxz/）