用旋转变换求线段最值

夏明

大连市第七十一中学曹天水老师的直播课“利用旋转变换求解线段最值问题”，选自辽宁教育学院“學到汇”公众服务平台“辽宁省初中数学学科周末名师公益课堂”，旨在贯彻落实国家“双减”政策，帮助广大师生自主学习和个性化提升.

旋转变换是各地中考数学试卷中常见的几何变换形式. 旋转中心、旋转角度、旋转方向是旋转变换的三大要素. 当两条线段有公共端点且不在同一条直线上时，常用旋转变换来解决问题. 相关的点在变换过程中形成运动轨迹，根据点的位置变化可明确线段最值的存在. 因此，遇到求线段最大值和最小值的问题，可利用旋转变换添加辅助线. 这在曹天水老师的直播课中体现得很充分.

题型1：结合垂线段最短求最值

例1  如图1，在Rt△ABC中，∠ACB = 90°，∠B = 30°，AC = 4，D为线段BC上一动点，∠DAE = 60°，AE = AD，连接CE，求线段CE的最小值.

分析：因为点D为线段BC上一动点，AE = AD，∠DAE固定不变，所以点D运动时，点E也随着运动. 已知点D在BC上运动，若能确定点E在哪条线上运动，则过点C作这条线的垂线段，这条垂线段就是CE的最小值.

由已知条件可知CE和CD是相等且共端点的两条线段，这就具备了旋转变换的条件. 如图2，结合∠1 = ∠2，把△ADB绕点A顺时针旋转得到△AEF. 把△ADC绕点A逆时针旋转得到△AEM. 点D在BC上运动，点E就在MF上运动. 因此，过点C作CH⊥EF，当点E运动到点H处时，CE最短.

解法1：如图2，延长AC到F，使AF = AB，连接 FE.

∵△ABC是直角三角形，AC = 4，∠B = 30°，

∴∠CAB = 60°，AB = 2AC = 8，∴AF = AB = 8.

∵∠DAE = ∠CAB = 60°，

∴∠DAE - ∠3 = ∠CAB - ∠3， 即∠1 = ∠2.

∵AE = AD，∴△AEF ≌ △ADB，

∴∠F = ∠B = 30°.

∵点 E在 FM上， ∴当CE⊥FM时，CE最短.

不妨作CH⊥FE，在Rt△CHF中，∠F = 30°，

∵CF = AF - AC = 4，∴在 Rt△CHF中，2CH = CF，

∴CH = 2，即CE最小值为2.

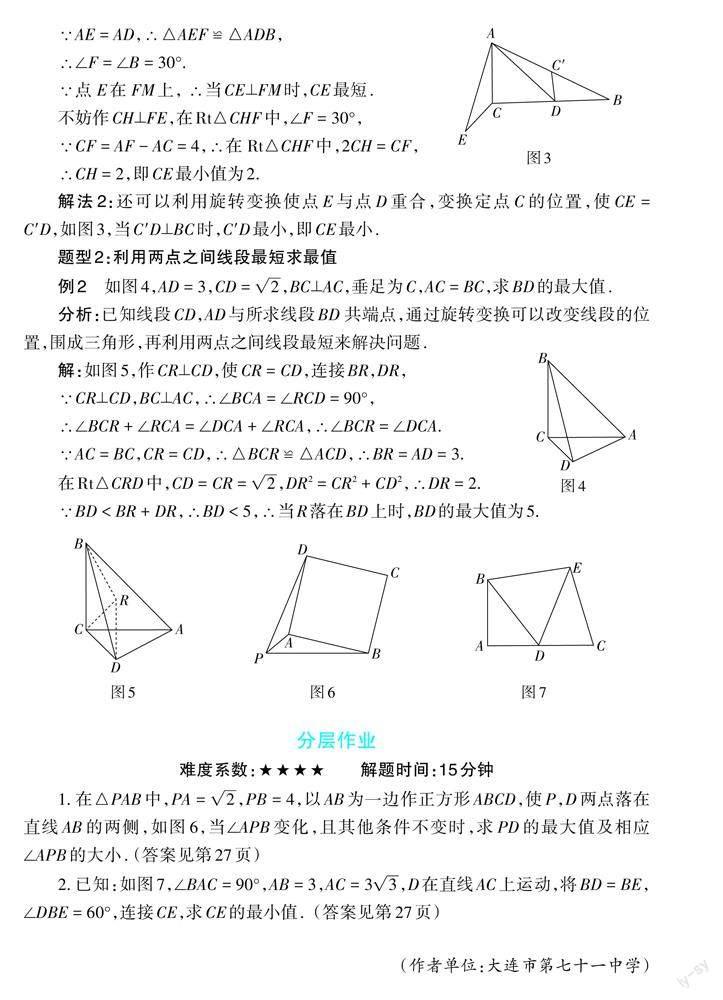
解法2：还可以利用旋转变换使点E与点D重合，变换定点C的位置，使CE = C'D，如图3，当C'D⊥BC时，C'D最小，即CE最小.

题型2：利用两点之间线段最短求最值

分析：已知线段CD，AD与所求线段BD 共端点，通过旋转变换可以改变线段的位置，围成三角形，再利用两点之间线段最短来解决问题.

解：如图5，作CR⊥CD，使CR = CD，连接BR，DR，

∵BD < BR + DR，∴BD < 5，∴当R落在BD上时，BD的最大值为5.

分层作业

难度系数：★★★★解题时间：15分钟

（作者单位：大连市第七十一中学）