高动态场景下的极化空时零陷展宽算法

李润，王垚，*，郝放，张明程

(1.中国电子科技集团公司第五十四研究所，石家庄 050081；2.哈尔滨工程大学 智能科学与工程学院，哈尔滨 150001)

卫星导航已经成为当今世界经济、社会、军事等领域的重要基础设施，卫星导航抗干扰技术广泛应用于飞行器、机载、弹载等高动态平台[1]。探索高动态场景下抗干扰算法优化对于提升卫星导航抗干扰的稳健性具有重要的理论和应用价值[2]。

面对干扰信号短时间快速变化的高动态场景，零陷展宽算法可以通过扩展波束零陷范围，确保快速移动的干扰不会移出零陷，保证抗干扰的稳健性[3-5]。同时，极化阵列具有自由度高、极化分址的优点，有助于克服干扰信号和导航信号来向接近时无法有效抑制的问题[6]。因此，多维域联合的零陷展宽算法成为高动态场景下抗干扰研究重要方向之一[7-9]。

目前，零陷展宽算法研究主要包括微分约束法、干扰加噪声协方差（interference-plus-noise covariance,INC）矩阵重构算法和协方差矩阵锥化（covariance matrix taper，CMT）算法3 种类型[10-11]。微分约束法通过对干扰导向矢量或者最优权值施加微分约束进行零陷展宽，但需知道干扰来向的先验信息，且约束增多会占据空间自由度[12]。INC 矩阵重构算法利用信号来向区域空间谱估计值重构INC 矩阵改变零陷宽度，但空间谱搜索会增加计算量，不能灵活控制零陷宽度[13]。CMT 算法通过构造锥化矩阵对接收信号采样协方差矩阵处理来实现零陷展宽，无需确定干扰信号来向信息，计算量较小、工程实现简单，使得CMT 算法成为零陷展宽算法研究的重要内容[14]。

20 世纪90 年代，Mailloux 首先提出空域下的CMT 零陷展宽算法，并进行了工程应用[15]。Mailloux提出在真实干扰信号附近设置多个虚拟干扰信号，通过虚拟协方差矩阵与真实协方差矩阵关系计算锥化矩阵，重构采样协方差矩阵实现零陷展宽，提高了应对干扰信号来向快速变化的能力[15]；Zatman通过增大干扰源带宽对协方差矩阵进行重构拓宽干扰零陷，具有不改变协方差矩阵中噪声项的优势[16]。21 世纪以来，国内学者引入了CMT 零陷展宽算法，围绕多维域和干扰来向统计模型进行了延伸研究。卢丹等[17]Xia 等[18]将零陷展宽算法从空域拓展到空时域、极化空时域，增加了抗干扰自由度，提高了干扰抑制的稳健性。李荣峰等从干扰来向统计模型角度出发，进行了CMT 零陷展宽算法优化研究，并证明了统计模型为高斯分布时的零陷展宽[19]。国内一些学者等分别提出了统计模型为伯努利分布[20]、Laplace 分布[17]和三角分布[21]时的CMT 零陷展宽算法，丰富了干扰来向统计模型的谱系，其中，Laplace 分布统计模型更能有效描述干扰来向运动状态[22]，适合高动态运动场景。概括而言，多维域联合的CMT 零陷展宽算法可以保证干扰和导航信号来波方向接近时，抗干扰性能的稳健性[23]。但目前对于多维域联合的CMT 零陷展宽算法研究主要基于均匀分布干扰来向扰动模型，对于基于Laplace分布的多维域零陷展宽算法研究尚不充分。

基于此，本文提出了一种用于高动态场景的极化空时多维域零陷展宽抗干扰算法。利用干扰信号来向扰动特点建立Laplace 分布模型，据此构造锥化矩阵，通过锥化矩阵与原始协方差矩阵重构采样协方差矩阵实现零陷展宽，从波束方向图、输出性能和卫星捕获结果3 方面进行仿真分析。算法有助于提升抗干扰性能稳健性，保障高动态场景下抗干扰算法的工程应用。

1 极化空时信号模型

极化空时多维域联合抗干扰技术是通过将一维的时域、频域或空域滤波拓展到时间、空间与极化三维域中，形成极化空时三维结构。极化阵元通道加入相同时间延迟等效为FIR 滤波器，可以在时域抑制干扰[24]；干扰信号和导航信号的极化参数差异及阵元位置的相位差可以在极化域、空域进行干扰抑制，故极化空时具备在三维域上抗干扰的能力。

本文首先建立极化空时信号模型，设阵元数为M，每个阵元级联K个时域抽头，时间延迟均为T。阵列由电偶极子对构成，可同时接收水平极化（H）和垂直极化（V）电磁波。布阵形式为均匀线阵，阵元间距为半波长。极化空时滤波结构如图1 所示。

图1 极化空时滤波结构Fig.1 Polarized space-time filtering structure

假设导航信号为L个，干扰信号为Q个，并且以平面波形式从远场入射，信号的方位角为θ，极化参量为 (γ,η)，那么阵列天线接收信号模型为

式中：fl和fq分别为导航信号和干扰信号的中心频率；sl(t)和sq(t)分别为导航信号和干扰信号的复包络；z(t)为 高 斯 白 噪 声 信 号 向 量；a(fl,θl,γl,ηl)和a(fq,θq,γq,ηq)分别为导航信号和干扰信号的极化空时导向矢量，推导过程如下。

定义均匀线阵的极化域、空域和时域导向矢量表达式分别为

式中：f为接收信号中心频率；F为采样频率。得到极化空时导向矢量表达式为

式中：“⊗”为Kronecker 乘积。

然后，根据最小方差无失真响应（minimum variance distortionless response，MVDR）波束形成准则，兼顾有用信号增益和系统输出功率最小化，得到极值函数：

式中：权值w=[w1,w2,···,w2M]T；R≜E{x(t)x(t)H}为接收信号协方差矩阵。构造拉格朗日乘子函数，得到最优权值向量为

2 极化空时CMT 零陷展宽算法

在极化空时信号模型框架下，优化CMT 零陷展宽抗干扰算法。首先，假设干扰信号来向变化服从Laplace 分布，通过假设的干扰加噪声协方差矩阵计算锥化矩阵，并对真实采样协方差矩阵进行锥化处理，进而结合MVDR 波束形成算法求取最优权值，实现极化空时零陷展宽。

假设第q个真实干扰的方位角、极化角、极化相位

由于导航信号功率相对于噪声、干扰很小，计算协方差矩阵时可忽略[25]，并且不同干扰之间、干扰与噪声之间相互独立，阵列接收信号采样协方差矩阵可近似为

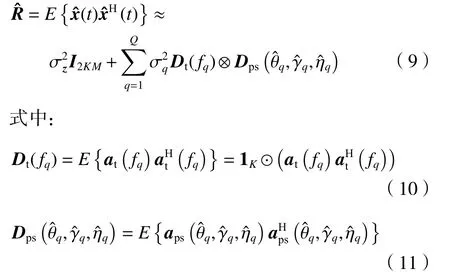
经公式推导得到

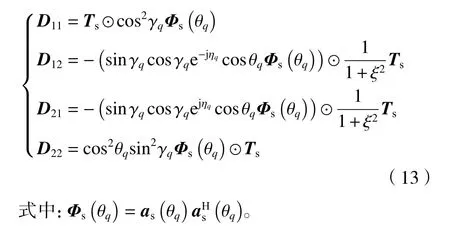
在式（13）中，空域CMT 矩阵Ts的（m,n）位置的元素为

将式（13）代入式（12），得到极化空域锥化矩阵为

最后得到极化空时联合锥化矩阵为

根据式（16），构造新的接收信号的采样协方差矩阵Rˆ ≈Ttsp⊙R，完成锥化处理。将采样协方差矩阵Rˆ替 换式（7）中理论协方差矩阵R，得到最优权值向量。

3 仿真分析

为验证本文算法的有效性，设计波束方向图、输出性能和卫星捕获结果3 个实验进行仿真分析。设置平台仿真参数：阵列分布为11 阵元极化等距线阵，抽头数为15 个，阵元间距为半波长，信号为1 个北斗B3 频点BPSK 信号和2 个覆盖全频点的宽带干扰信号。以下实验均采用此组仿真数据。

1 ）实验1：波束方向图仿真

设定导航信号来波方向为0°，极化相角、相位差为（20°, 25°），信噪比（signal to noise ratio，SNR）为−20 dB；干扰信号来波方向为−50°和50°，极化相角和 极 化 相 位 差 为（30°, 30°）、（60°, 65°），干 噪 比（interference to noise ratio，INR）为70 dB；输入噪声为高斯白噪声；展宽参数 λmax为0.5。仿真对比常规MVDR 算法和本文算法的自适应波束方向图，以观察干扰信号来向上形成的零陷深度和宽度。仿真结果如图2 和图3 所示。

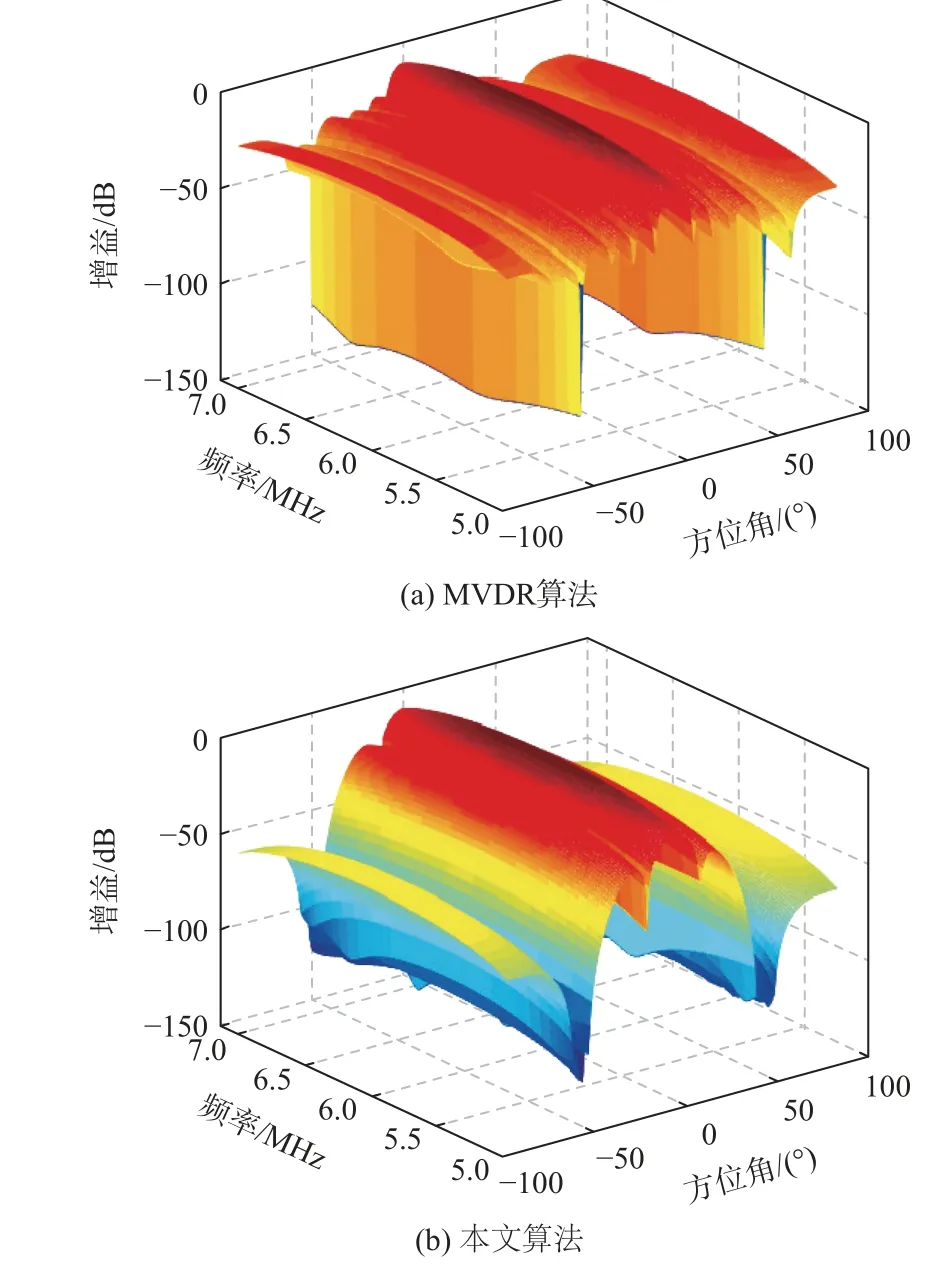
图2 空域波束方向图Fig.2 Beam pattern with spatial domain

图3 极化域波束方向图Fig.3 Beam pattern with polarization domain

由图2 可见，MVDR 算法空域波束方向图在干扰来向−50°和50°形成较窄的零陷，适用于干扰角度位置不变的干扰，而本文算法在干扰来向形成宽零陷，并且在信号来波0°方向增益明显。由图3 可见，MVDR 算法极化域波束方向图在极化相角和极化相位差（30°, 30°）、（60°, 65°）方向形成窄零陷，而本文算法可以形成10°以上的宽零陷。可以观察到，零陷展宽后的零陷深度低于MVDR 算法，这是由于CMT 算法通过多个虚拟干扰代替单个干扰，将单个干扰的功率均分，导致零陷展宽的同时深度变浅。结果表明，本文算法在干扰信号来向上零陷展宽效果显著，提高了权值与动态干扰的匹配度，能够满足高动态下的干扰抑制需求。

2 ）实验2：算法输出性能仿真

输 出 信 干 噪 比（signal to interference plus noise ratio，SINR）是指输出信号与干扰和噪声之和的比值，数值越大抗干扰性能越好[26]。本实验仿真分析输入SNR、快拍数及干扰和导航信号方位角来向差值对输出SINR 的影响。

为模拟高动态仿真环境，依据文献[27]对高动态的定义，假设抗干扰天线距离干扰源1 km，以6 km/s 的速度作高速直线运动，在5 ms 权值计算期间，干扰源相对天线角度偏移最大为2°，故设定2°的动态干扰，2 个干扰分别从−50°～−48°、50°～52°变化，即批处理权值作用于变化2°后的接收数据。

① 输入SNR 对输出SINR 的影响。设定输入SNR 在−30～0 dB 变化，蒙特卡罗次数为200 次，仿真得到MVDR 算法和本文算法阵列输出SINR 随输入SNR 变化曲线，如图4 所示。

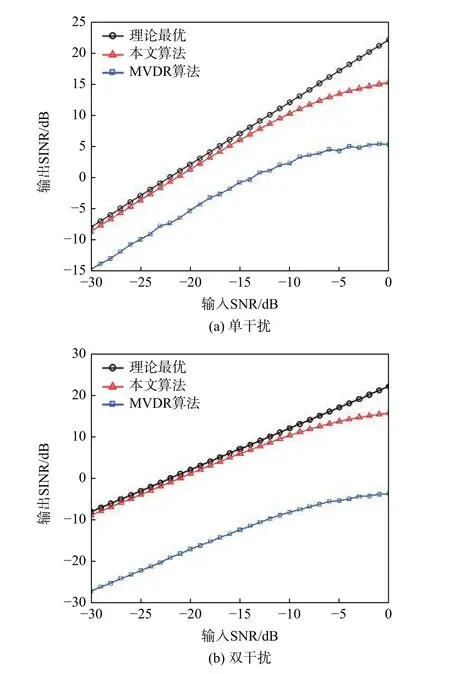
图4 单干扰与双干扰下输出SINR 随输入SNR 变化关系Fig.4 Output SINR versus input SNR under single interference and two interferences

2 种算法均随输入SNR 增大而逐步提升，当输入SNR>−10 dB 时，导航信号功率增大，会将导航信号当作干扰信号进行抑制，形成小零陷，导致输出SINR 相对于最优曲线变差的程度加剧。在动态干扰条件下，本文算法相比于MVDR 算法，单干扰时高10 dB 左右，双干扰时高20 dB 左右。这是由于MVDR 算法权值计算速率滞后于干扰信号来向变化速率，导致干扰移出零陷，输出SINR 大幅降低。结果表明，本文算法相比MVDR 算法，提高了信号的输出SINR，抗干扰性能优越。

② 快拍数对输出SINR 的影响。在工程应用中，接收数据的统计特性是不易求解的，故使用采样协方差矩阵替代统计协方差矩阵，快拍次数的选择会直接影响协方差矩阵的可靠性。动态干扰状态下，设定快拍数在10～1 500 变化，蒙特卡罗次数为200 次，得到随快拍数变化输出SINR 见图5。

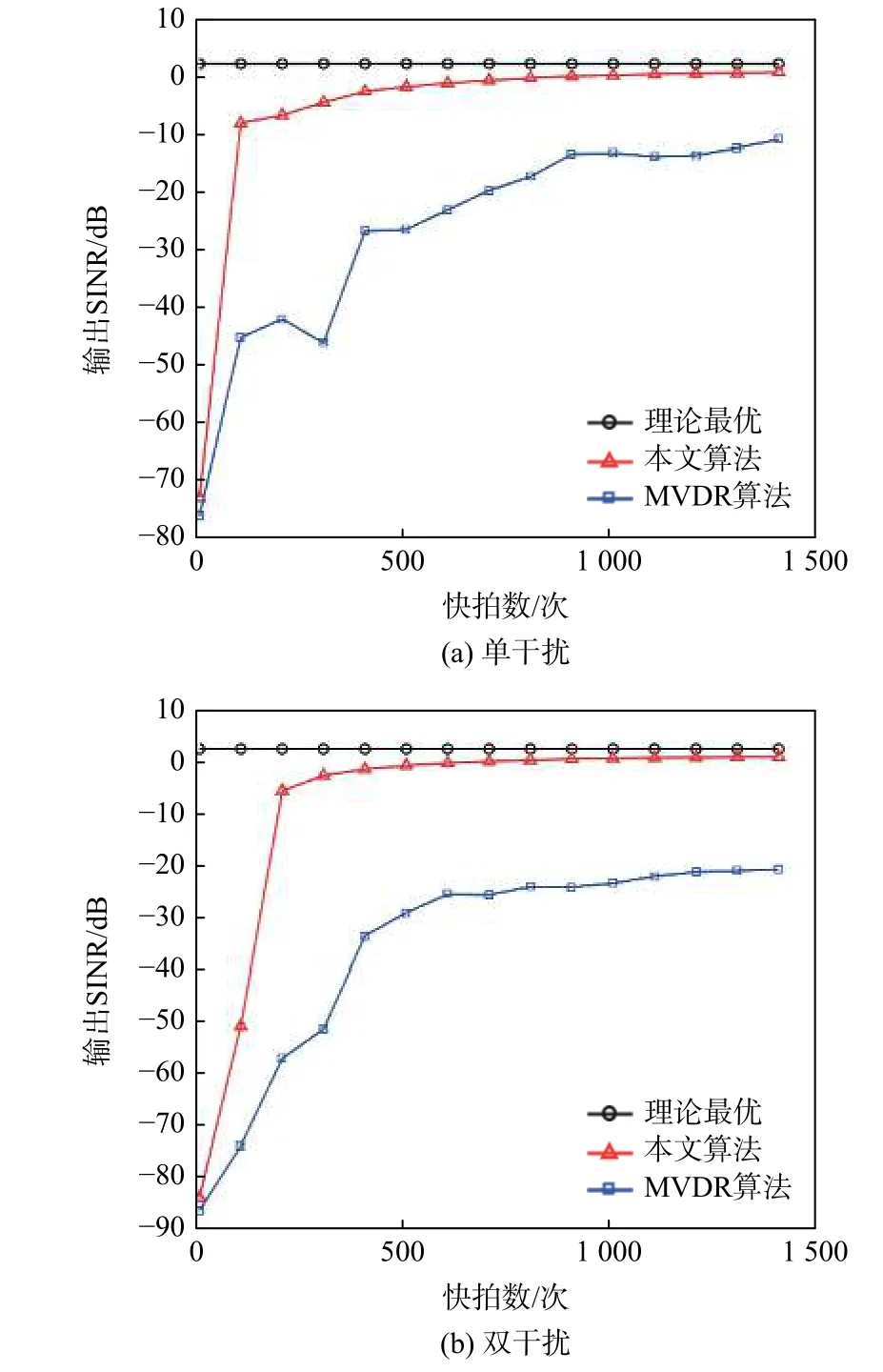
图5 单干扰与双干扰下输出SINR 随快拍数变化关系Fig.5 Output SINR versus number of snapshot under single interference and two interferences

2 种算法均随快拍数增加而逐步收敛，当快拍数到500 时本文算法达到收敛，而MVDR 算法由于角度失配的原因，达到收敛需要更多的快拍数。在动态干扰条件下，本文算法相比于MVDR 算法，单干扰时高10 dB 左右，双干扰时高20 dB 左右。这是由于MVDR 算法无法抑制动态干扰导致干扰信号功率增大，输出SINR 较低。结果表明，本文算法收敛速度较快，输出SINR 接近于理想状态，可以有效解决零陷与采样数据中干扰来波方向不匹配的问题。

③ 干扰和导航信号来向方位角接近时对输出SINR 的影响。设定导航信号方位角来向0°不变，干扰信号来向在−10°～10°变化，蒙特卡罗次数200 次。当干扰和导航信号方位角差值接近时，仿真得到空时算法和极化空时算法的输出SINR，如图6 所示。结果表明，随着干扰和导航信号方位角差值变小，空时算法输出SINR 大幅降低，差值为0 时急剧下降，而极化空时算法能够保持稳定的输出SINR。验证了来向接近的信号可以根据极化域特征差异进行区分的优势。

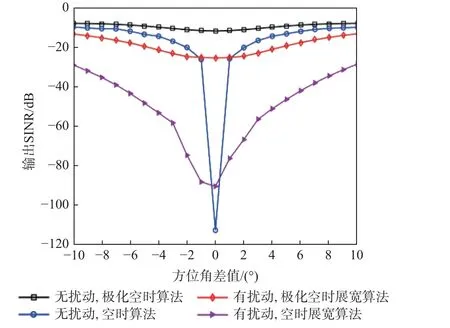
图6 输出SINR 随干扰和导航信号方位角差值的关系Fig.6 Output SINR versus azimuth difference of jamming signal and navigation signal

3 ）实验3：卫星捕获结果仿真分析

卫星捕获结果可以直接表征抗干扰算法的可行性。设定导航信号SNR 为−20 dB，INR 为70 dB。通过并行码相位捕获，MVDR 算法和本文算法捕获结果如图7 所示。结果表明，MVDR 算法无法捕获卫星信号，而本文算法卫星捕获结果出现了明显的峰值，说明卫星信号捕获成功，能够有效抑制高动态下的干扰信号，验证了算法的可行性。

图7 卫星捕获结果Fig.7 Results of satellite capture

4 结 论

高动态场景下，针对干扰源快速运动导致抗干扰性能失效的问题，本文提出了一种极化空时多维域零陷展宽抗干扰算法，有助于推动工程应用，主要结论如下：

1）构建了极化空时多维域抗干扰模型，解决了干扰和导航信号来向相同时空域滤波无法抑制的问题。

2）将零陷展宽算法从空时域拓展到极化空时域，构建了基于Laplace 分布的极化空时CMT 算法，实现了多维域下零陷展宽优化。

3）通过对波束方向图、输出性能和卫星捕获结果进行仿真分析，验证了与传统的MVDR 算法相比，本文算法干扰零陷范围灵活可控，阵列输出SINR 单干扰提高了10 dB 左右，双干扰提高了20 dB左右，并且卫星信号捕获成功。