基于自适应神经网络鲁棒观测器的EHA故障诊断与容错控制

赵杰彦，胡健，*，姚建勇，周海波，王俊龙，曹萌萌

(1.南京理工大学 机械工程学院，南京 210094；2.中南大学 高性能复杂制造国家重点实验室，长沙 410012)

电静液作动器(electro-hydrostatic actuator，EHA)是一种功率电传作动器，其优势在于：能源系统和液压用户集成在一起，减少了液压管路质量和液压油泄漏污染[1]。EHA 高度集成了功率放大电路、电机、柱塞泵、单向阀、溢流阀、液压油缸等器件于一体，因而其故障种类更多，包括控制器故障（如DSP 程序异常）、电机电路故障（如斩波、逆变电路短路或断路、电机绕组短路或断路、传感器故障）、液压管路故障（如油液污染引起的管路或阀芯堵塞、管路严重泄漏、泵输出流量或压力异常）。由于安装各类型传感器需要额外附加一部分质量同时占用机舱体积，在航空航天等应用场景下，不能盲目地增加传感器的数量，这就需要在有限传感器的基础上，设计可靠、有效的故障检测策略，来实现EHA 各类型故障的检测[2-5]。

故障诊断可以分为基于信号的故障诊断和基于模型的故障诊断。基于信号的故障诊断依赖于信号测量及数据处理技术，提取故障特征以评估系统是否异常。2019 年，浙江理工大学陈换过团队建立基于自组织特征映射神经网络（self-organizing feature map, SOM）的 EHA 故障诊断模型，并以神经元反馈分布作为故障标识，进行故障诊断[6]；2020 年，该团队在原有SOM 神经网络的基础上，引入 主 成 分 分 析 法（Principal Component Analysis,PCA）对输入数据降维，并设置竞争域值贡献率，提出基于PCA 的自组织特征映射神经网络（PCASOM）算法，对EHA的油滤堵塞故障进行诊断[7]，对故障状态的识别率可达90%。

一般而言，基于信号的故障诊断较准确、虚警率较低，但数据处理量较大，对硬件设施要求较高。基于模型的故障诊断则利用冗余的系统解析模型输出与系统真实输出产生残差，进而判别系统故障与否[8-9]，易于在线实现，但需要建立较精准的数学模型。哈尔滨工业大学沈毅团队较早地开展了液压系统在线故障检测研究，2018 年该团队提出了一种基于H−/L∞观测器的故障检测方法，利用有限频域H−性能指标来度量残差的故障敏感度, 并且针对峰值有界的干扰信号, 通过L∞范数来分析干扰对残差的影响，由于模型存在不确定性，带来的误差大于故障引起的残差，在故障幅值特别小时效果并不理想[10]。

上述团队的主要研究成果体现在获取故障信息，但在工程实践中仅获取故障信息还不够，为达到更好的跟踪精度和鲁棒性，需要进一步设计容错控制器。按照实现原理，容错控制可以分为被动容错控制和主动容错控制[11-12]。其中，被动容错控制将系统故障看作干扰，本质是一个鲁棒控制器，结构较简单、易于工程实现，Kim 等使用反演法设计了自适应鲁棒控制器实现对故障的被动容错，但该方法缺乏针对性，因而系统的整体控制性能一般[13]。而主动容错控制则利用在线故障检测结果做出针对性的补偿，以使系统性能不受故障的影响或将故障引起的影响降至最低，因此在故障发生后仍能保持很好的跟踪精度[14-15]。戴邵武等在应用自适应卡尔曼滤波进行系统状态和故障同步估计的基础上，通过故障信息和状态估计进行状态反馈，对闭环系统进行极点配置，从而修正执行器故障造成的系统误差，实现了容错控制，但是没有考虑参数不确定性、参数时变等因素，因而还有改进空间[16]。

针对上述分析中EHA 的特点及不同故障诊断方法、容错控制方法的优缺点，采用基于模型的主动容错控制方法，降低硬件开支的同时利用径向基函数（radial basis function，RBF）神经网络逼近系统中的非线性项，利用鲁棒观测器获取系统真实状态与故障值，利用参数自适应率来获取真实参数供控制器使用，同时控制器还将观测到的故障值、非线性等予以补偿，实现了复杂工况下的高跟踪精度和对故障的良好鲁棒性。

1 系统建模

EHA 基本工作原理如图1 所示。伺服电机驱动双向液压泵旋转，产生高压油经过液压阀后流入作动筒，活塞杆在压差的作用下克服负载，推动飞机舵面偏转；通过传感器反馈作动器的位移，控制电机的转速和方向，实现舵面偏转的动态控制。

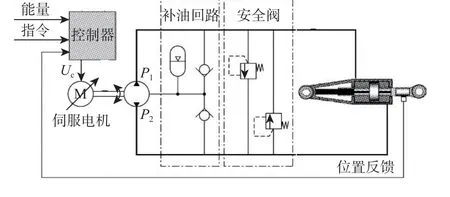
图1 EHA 系统结构Fig.1 Structure of EHA system

根据牛顿运动定律，EHA 的数学模型表示为

式中：P1、P2分 别为油缸进油口、出油口压强；Ac为液压缸活塞面积；M为液压缸活塞和负载总质量；B为黏滞阻尼系数；k为刚度系数；x为活塞杆位移；x˙ 为 活塞杆速度；x¨ 为活塞杆加速度；Ff为故障引 起的负载变化，Fd为非线性引起的负载变化，且|Ff|≤σ1，|Fd|≤σ2。

式中：Q1和Q2分别为进油口和出油口液压油流量；Dp为 泵排量；ωp为 泵转速，即实际控制量；Lp为液压泵外泄漏系数；Pa、Pb分别为液压泵出油口、回油口压力；P0为液压泵的内泄漏口压力。

根据流量、压力关系可得

式中：Qi和Qo分 别为油缸进油和回油流量；Va为液压管路和油缸平均容积；βe为等效弹性模量；Lep为泄漏系数。假设油缸、管路密封良好，不向系统外部泄漏液压油，即Qi=Q1，Qo=Q2，La=Lep+Lp。

整理式(1)～式(3)：

式中：f、d分别为故障状态和扰动状态。按如下规则选取系统状态：

2 观测器设计

将系统状态方程进一步整理得

式中：X=[x1x2x3f]T。

式中：g(X,U)=d+θ3∗U为系统中存在的非线性项。

由于RBF 具有全局逼近能力，避免了误差反向传播（back propagation，BP）神经网络的局部最优问题，而且拓扑结构紧凑，收敛速度快，本文采用如图2 所示的RBF 神经网络对g(X,U)逼近。

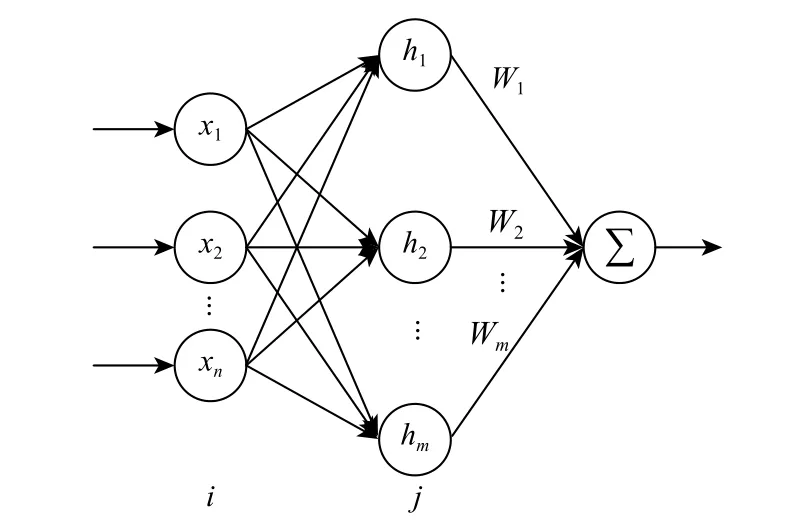
图2 RBF 神经网络结构Fig.2 Structure of RBF neural network

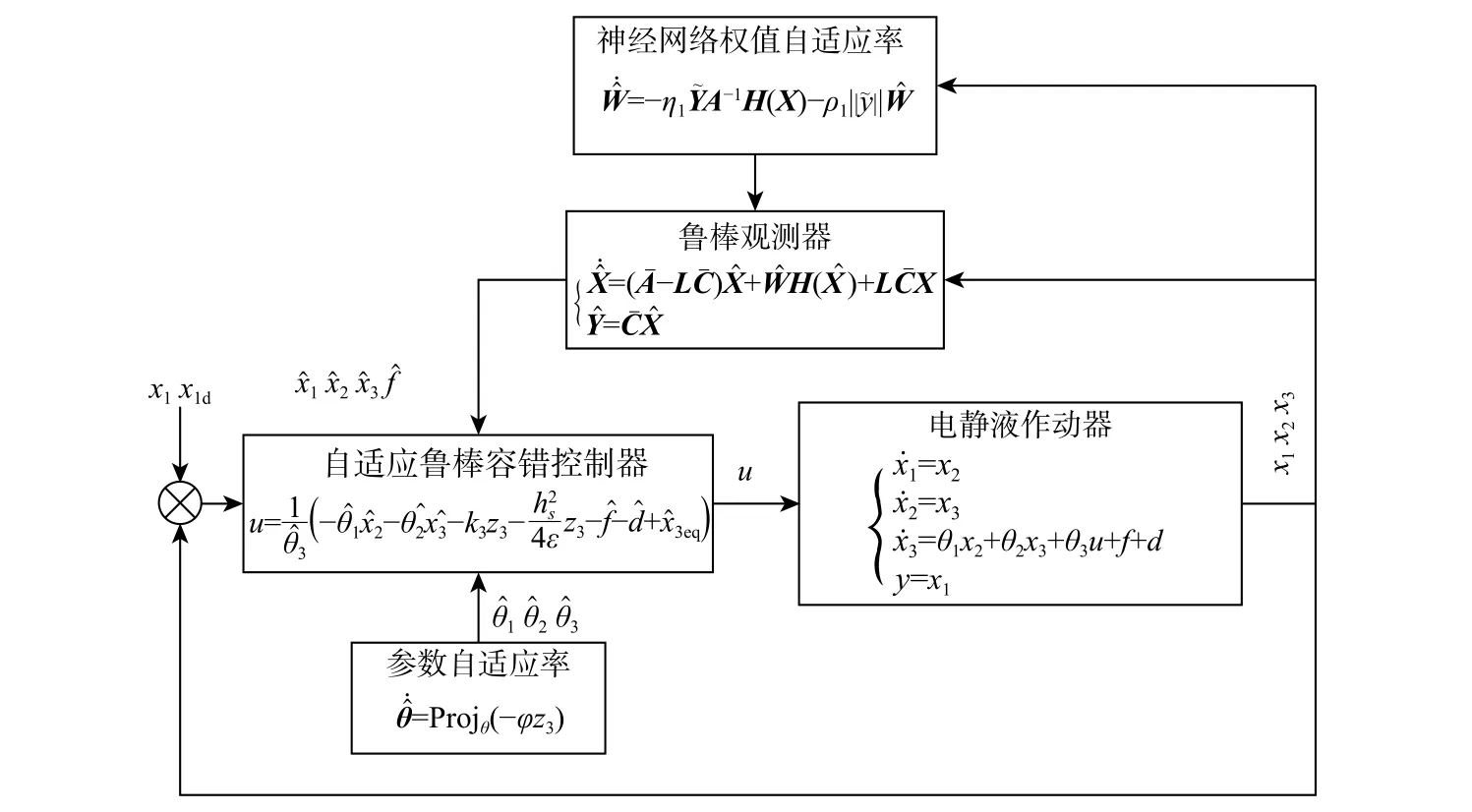
图3 控制器结构Fig.3 Structure of controller

令X˜=X−Xˆ表示观测器的估计误差，两边同时求导有

3 控制器设计

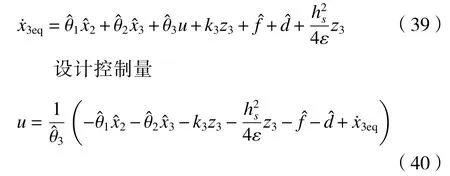
步骤 4 设计参数自适应律。为使参数不确定性对控制性能的影响尽可能降低，设计一个参数不连续映射，用以估计系统参数。在已知系统的不确定性有界的前提下，设计参数自适应率为

式中：Projθ(.i) 为变量i的映射。

上述设计满足如下性质：

步骤 5 设计故障检测策略。由状态观测器的观测误差，定义如下残差 用于故障检测：

当传感器发生故障时，残差ex(t)将变大，一旦超过一定阈值，则可判定系统存在故障。当传感器工作正常而执行器发生故障时，ex(t)不会发生明显变化，但fˆ可以检测出系统中的故障，此时可以通过检测fˆ的值是否超过一定阈值来判断系统是否发生故障。这样，通过综合ex(t)和fˆ 的检测结果判断系统中是否发生了故障，从而提高系统故障的识别准确率。

4 稳定性证明

定理3 当故障f对系统造成的影响不可忽略时，系统可以按照规定的状态对速度和位置进行跟踪，跟踪误差被限制在一个已知函数内，系统处于有界稳定状态，保证了系统稳定性[21-23]。

证明 定义如下Lyapunov 函数：

由以上证明过程可以得出，控制器具有以 λ为指数收敛速率的瞬态表现，能够实现有界稳定。

5 仿真结果

3）基于BP 神经网络的自适应容错鲁棒控制器（BP-FTARC）。采用参考文献[20]提出的观测器，在此基础上结合本文设计的自适应容错鲁棒控制器，并选取K1= 400，K2= 600，K3= 350，观测器增益L=600。

4）本文提出的基于自适应神经网络鲁棒观测器的容错控制器（RBF-FTARC）。为了更好逼近未知参数，观测器中融合了RBF 神经网络，前馈项、线性反馈项、鲁棒项等均按照第3 节所述设计，并选取K1= 400，K2= 600，K3= 350，观测器增益L=600。

选用以下3 个性能指标用于衡量每种控制算法的质量，即跟踪误差的最大值、平均值和标准差，分别定义如下[24]：

给定期望位置曲线为正弦信号时，各控制器跟踪误差如图4 所示。

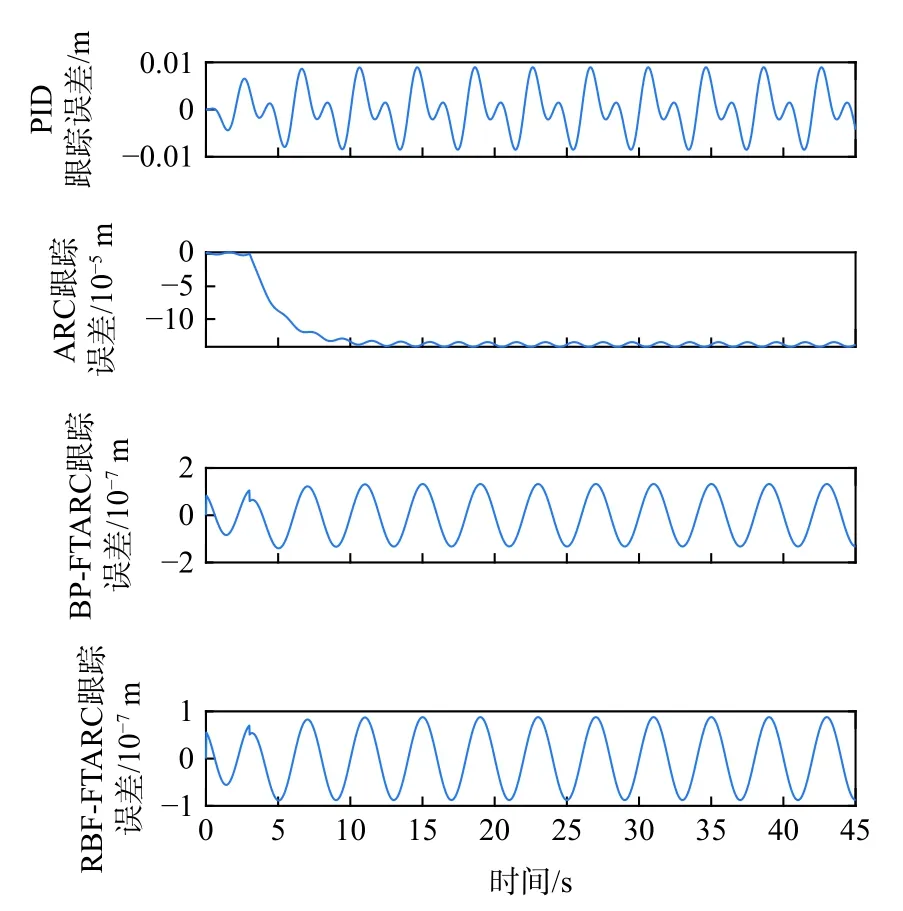
图4 各控制器跟踪误差曲线Fig.4 Tracking error curves of each controller

由图4 可见，在跟踪正弦曲线时，PID 控制器跟踪精度最低，跟踪误差可达0.01 m；ARC控制器在没有故障时精度较高，约为2×10−6m，故障发生后跟踪精度显著变差，达到1.4×10−4m；尽管BP-FTARC控制器对故障有较好鲁棒性，但是由于RBF 收敛速度比BP 显著提高，运算量显著降低，且不容易陷入局部最优，更容易得到最优解，在本文设计的RBFFTARC 控制器中予以补偿后，能实现更高的跟踪精度，在无故障时误差约为5×10−8m，在故障发生后跟踪误差仍旧小于1×10−7m，显著优于BP-FTARC控制器。

给定期望位置曲线为正弦信号时，3 种控制器性能指标比较如表1 所示。

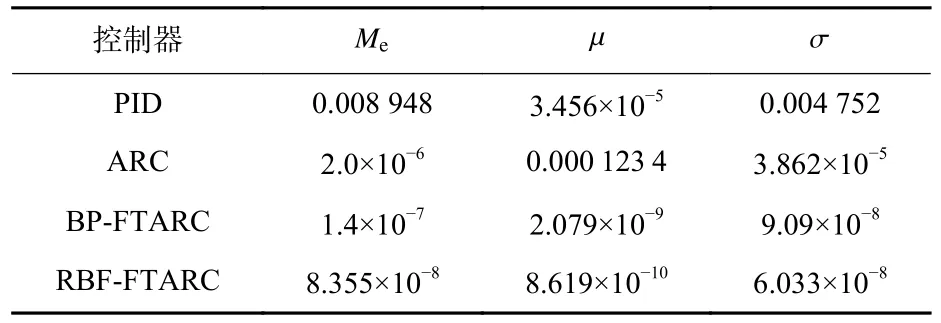
表1 正弦信号工况下的性能指标Table 1 Performance index under sinusoidal signal condition

由表1 可见，在跟踪正弦曲线时，3 个控制器各自跟踪误差的最大值、平均值、标准差3 项指标，FTARC 控制器都明显优于PID 和ARC 控制器3～5 个数量级。由此可见，本文所设计自适应容错鲁棒控制器在精准观测了系统内部各状态的基础上，能够及时准确观测故障信号并予以补偿，且同时考虑了参数不确定性，因而其性能指标也最优。

图5～图7 为跟踪正弦曲线时内部状态x1、x2、x3及其观测误差曲线。可见，各状态的观测误差约为其真实幅值的1‰，跟踪精度较高且能够及时修正故障（t=3 s 处）引起的误差，表明非线性观测器对模型内部状态观测效果良好。

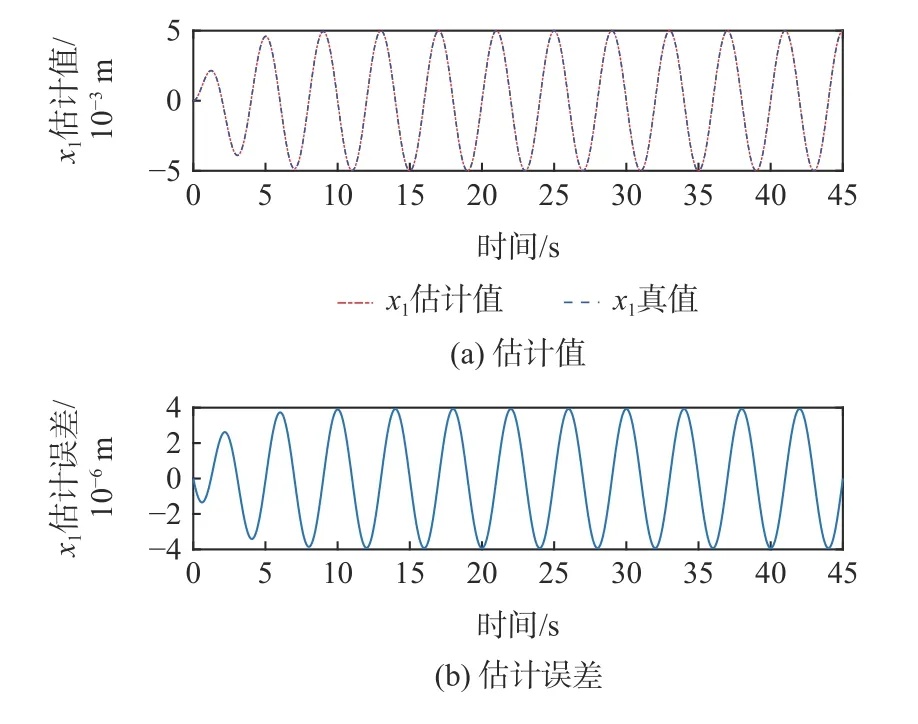
图5 状态x1 估计值及估计误差Fig.5 Estimation value and error of state x1

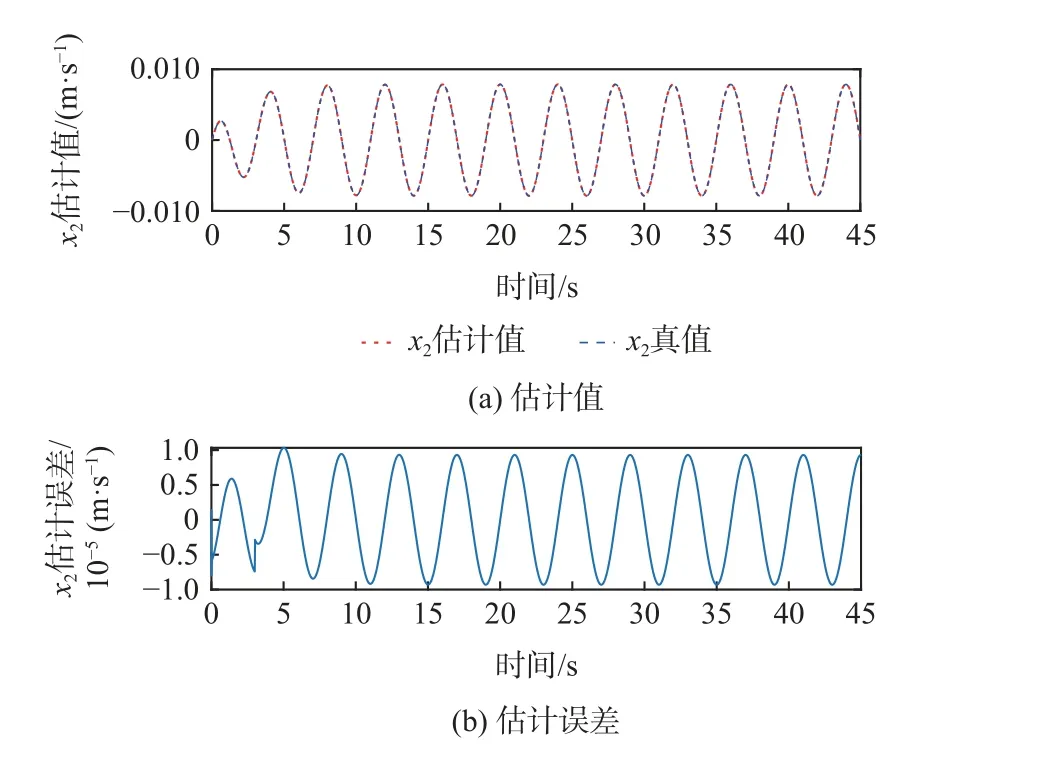
图6 状态x2 估计值及估计误差Fig.6 Estimation value and error of state x2

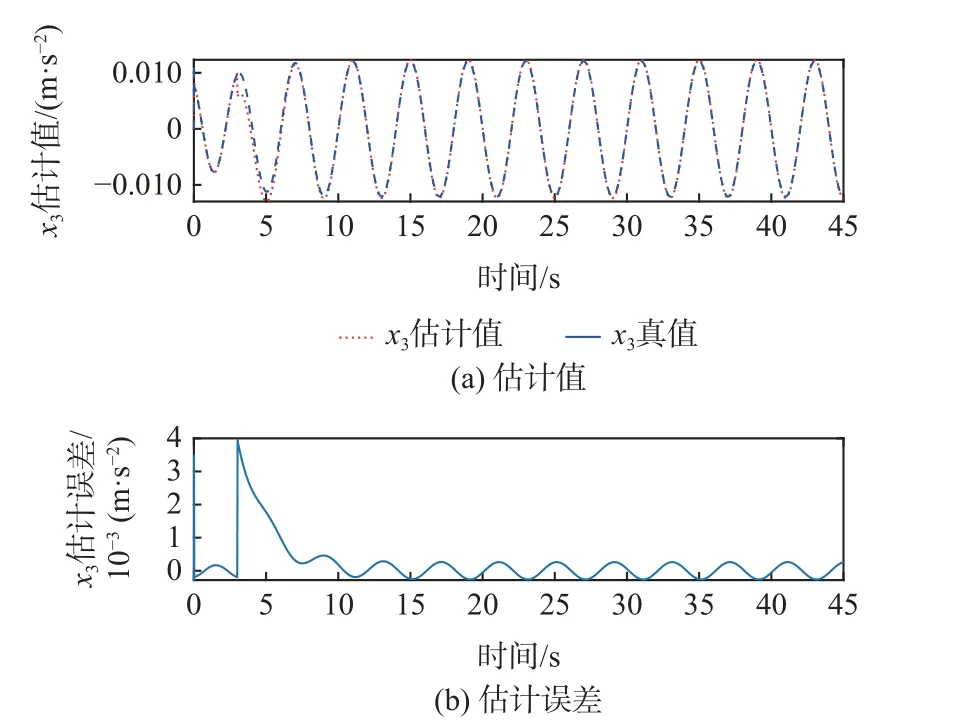
图7 状态x3 估计值及估计误差Fig.7 Estimation value and error of state x3

图8 中，t=3 s 时，残差显著增大，并超过设定的阈值，因而判定系统存在故障，对照仿真时注入的故障函数，能够发现残差突变的时刻与故障注入时刻一致，证明故障诊断方法有效。在整个仿真过程中，对故障的估计误差最大约3×10−4，显著低于故障幅值，表明本文设计的观测器具有良好的精度与鲁棒性。

图8 故障fx 估计值及估计误差、残差Fig.8 Estimation value, and error and residual of fault fx

图9 为正弦工况下的参数与非线性项估计曲线。模型中的3 个参数均能从估计值逐渐回归到真值，说明所设计的参数自适应律能够很好的发挥作用，所设计的RBF 神经网络也较精确的逼近了模型中的非线性项，说明了所设计的方法有效且性能良好。

图9 参数与非线性项估计曲线Fig.9 Estimation of parameter and nonlinear term

6 联合仿真验证

在MATLAB/Simulink 环境下完成控制器验证后，为进一步检验真实工况中本文控制器的使用效果，采用AMESim 与MATLAB/Simulink 联合仿真。

LMS Imagine.Lab AMESim 为多学科领域复杂系统建模仿真平台，本文主要使用该平台的液压库、液压元件设计库来搭建如图10 所示的EHA 仿真模型[25]。模型经AMESim 编译后生成.ame 文件，再链接至Simulink，生成如图11 所示的.slx 文件，并在此基础上按照设定的时间、步长等参数进行仿真，实现AMESim 和Simulink 的实时数据交互，同时将仿真数据存入.data 文件，最终导入MATLAB脚本程序完成数据分析与图形绘制。

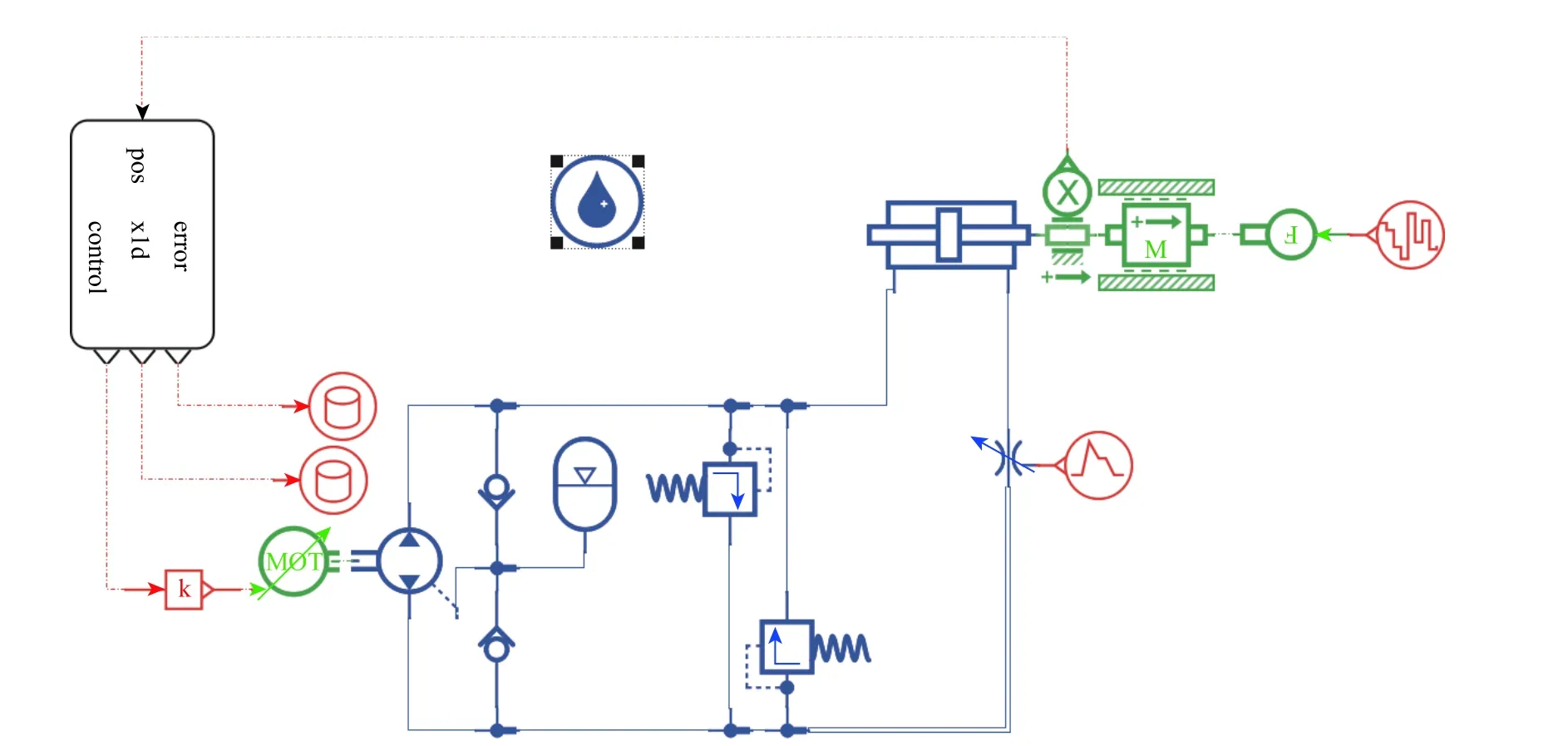
图10 AMESim 仿真平台搭建的EHA 模型[25]Fig.10 EHA model based on AMESim simulation platform[25]

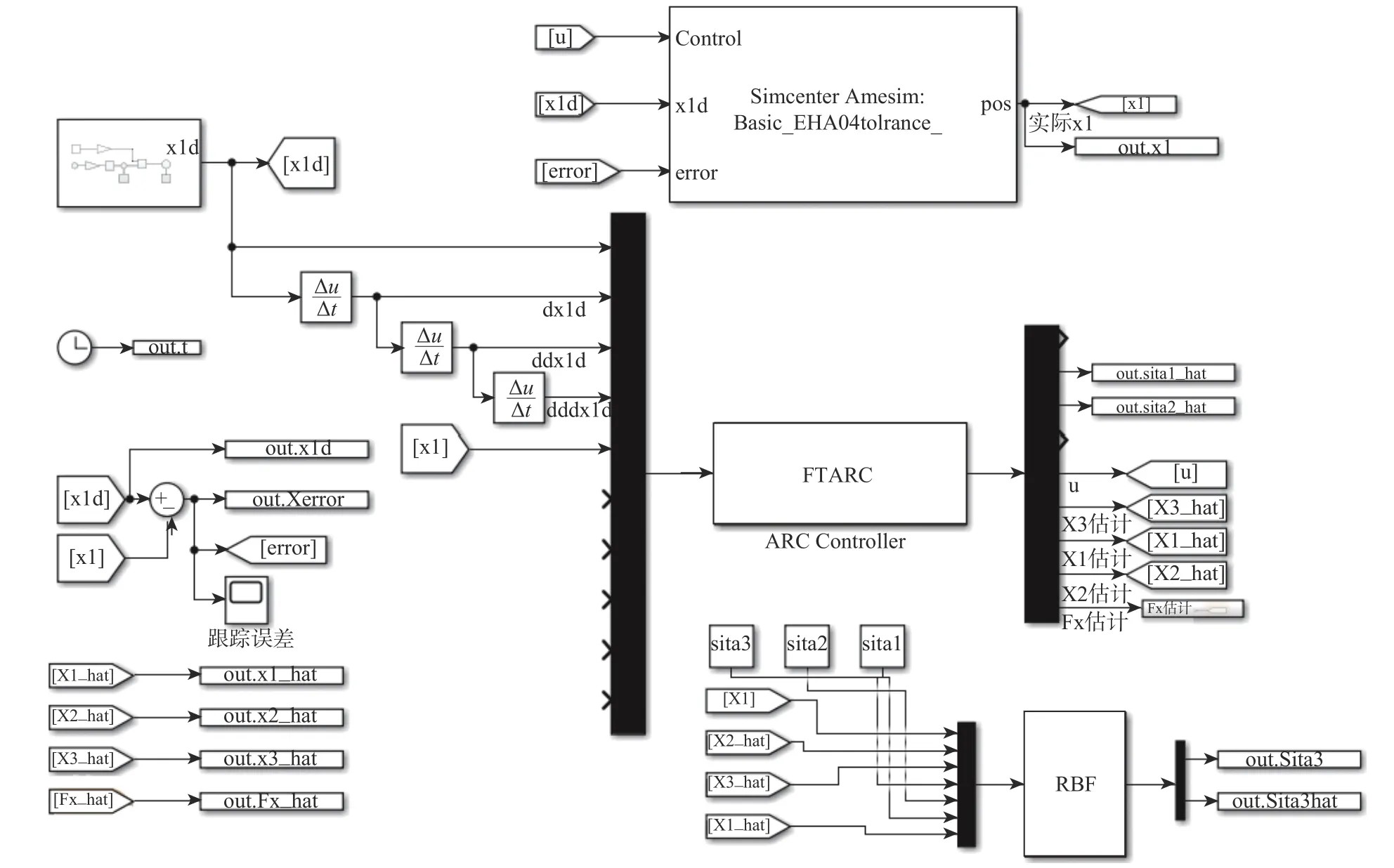
图11 AMESim/Simulink 联合仿真模型框图Fig.11 Block diagram of AMESim/Simulink co-simulation model

联合仿真所选取的参数及其取值如表2 所示。

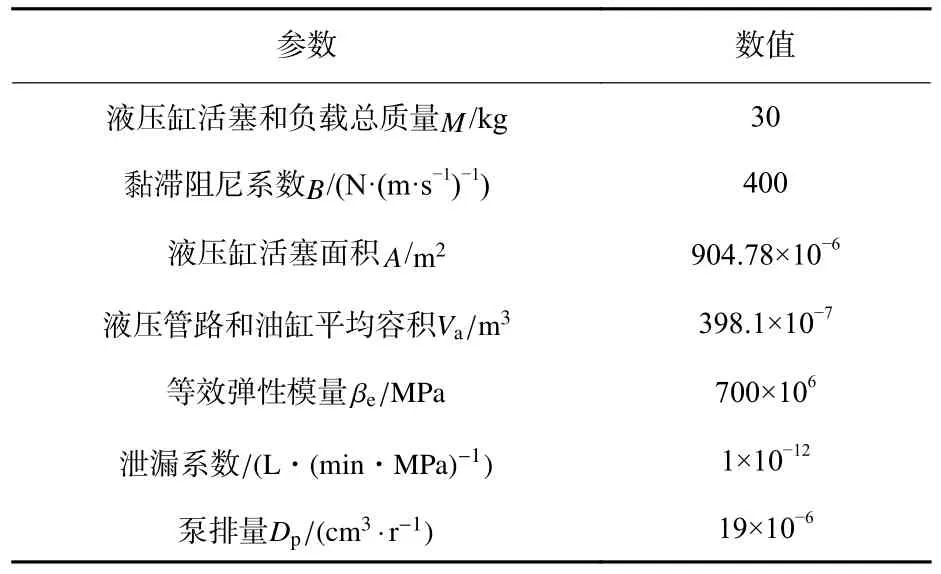
表2 联合仿真系统参数Table 2 Parameter of co-simulation system

为进一步验证本文所提控制策略的有效性，联合仿真环节继续采用PID、ARC、BP-FTARC 和本文设计的RBF-FTARC 四种控制器来对比跟踪性能。

3）BP-FTARC。采用参考文献[20]提出的观测器，在此基础上结合本文设计的自适应容错鲁棒控制器，并选取K1= 653，K2= 230，K3=230，观测器增益L=69。

4）RBF-FTARC。即本文提出的基于观测器的自适应容错鲁棒控制器，为了更好逼近未知参数，观测器中融合了RBF 神经网络，前馈项、线性反馈项、鲁棒项等均按照前文所述设计，并选取K1=653，K2= 230，K3= 230，观测器增益L=69。

给定曲线及各控制器跟踪误差如图12 所示，各控制器性能指标如表3 所示。

表3 工况1 下各控制器性能指标Table 3 Performance index of each controller under condition 1

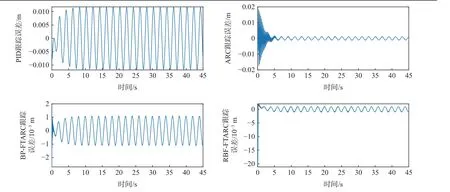
图12 工况1 下各控制器跟踪误差Fig.12 Tracking error of each controller under ideal working condition

由图12 和表3 可见，在理想工况1 时，4 种控制器跟踪精度都比较高，但由于本文设计的RBFFTARC 采用了状态观测器、故障补偿项、鲁棒项等措施，性能指标为4 种控制器中最优，跟踪精度比ARC 控制器提高50%。

2）工况2。液压系统在运行过程中如混入金属碎屑、颗粒粉尘等，容易引起管路或阀芯堵塞。设计工况2 对此类故障进行仿真，跟踪正弦位置曲线x1d=0.05+0.02sin(0.5πt)(1−e−0.5t)。t=5～10 s 发生液压管路堵塞故障。

给定曲线及各控制器跟踪误差如图13 所示，各控制器性能指标如表4 所示。

表4 工况2 下各控制器性能指标Table 4 Performance index of each controller under condition 2

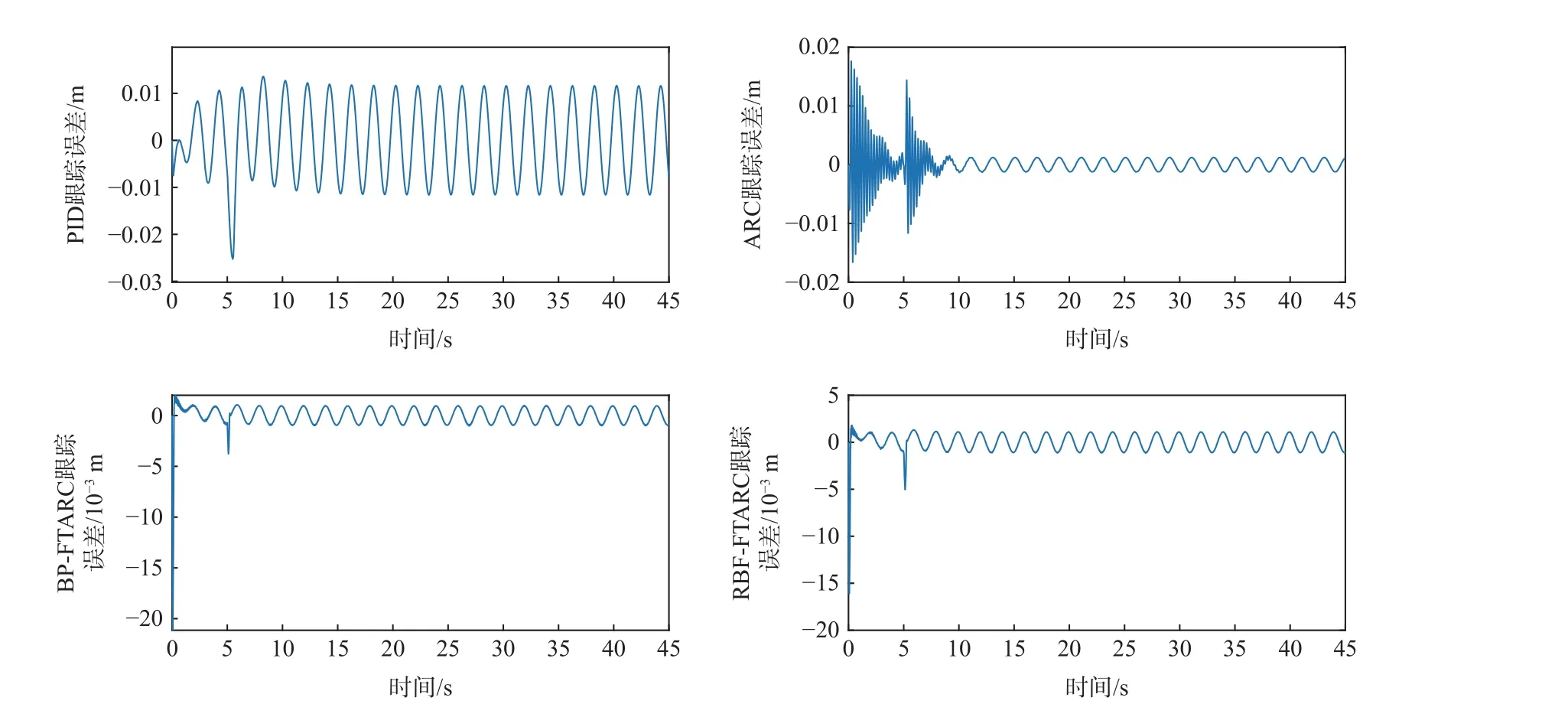
图13 工况2 下各控制器跟踪误差Fig.13 Tracking error of each controller under pipeline blockage condition

对比图13、表4 和图12、表3 可见，在工况2 下，系统受管路堵塞故障的影响，工作条件比理想工况1 明显恶劣，此时4 种控制器的平均跟踪误差均比理想工况1 条件下有所增大；尽管工况2 更为恶劣，4 种控制器性能指标均有下降，但是由于本文设计的RBF-FTARC 在设计时采用了状态观测器、故障补偿项、鲁棒项等措施，性能指标为4 种控制器中最优，跟踪精度比ARC 控制器提高约50%，比PID 提高约60%。

3）工况3。由于液压系统的工作环境比较恶劣，载荷重，冲击力大，液压系统油缸、活塞的损坏可能导致内泄漏的发生，针对内泄漏问题，设计工况3，跟踪高频的正弦位置曲线x1d=0.05+0.02sin(0.5πt)·(1−e−0.5t)。其中，包含泄漏故障，泄漏系数La=5 L /(min·MPa)。

给定曲线及各控制器跟踪误差如图14 所示，各控制器性能指标如表5 所示。

表5 工况3 下各控制器性能指标Table 5 Performance index of each controller under condition 3

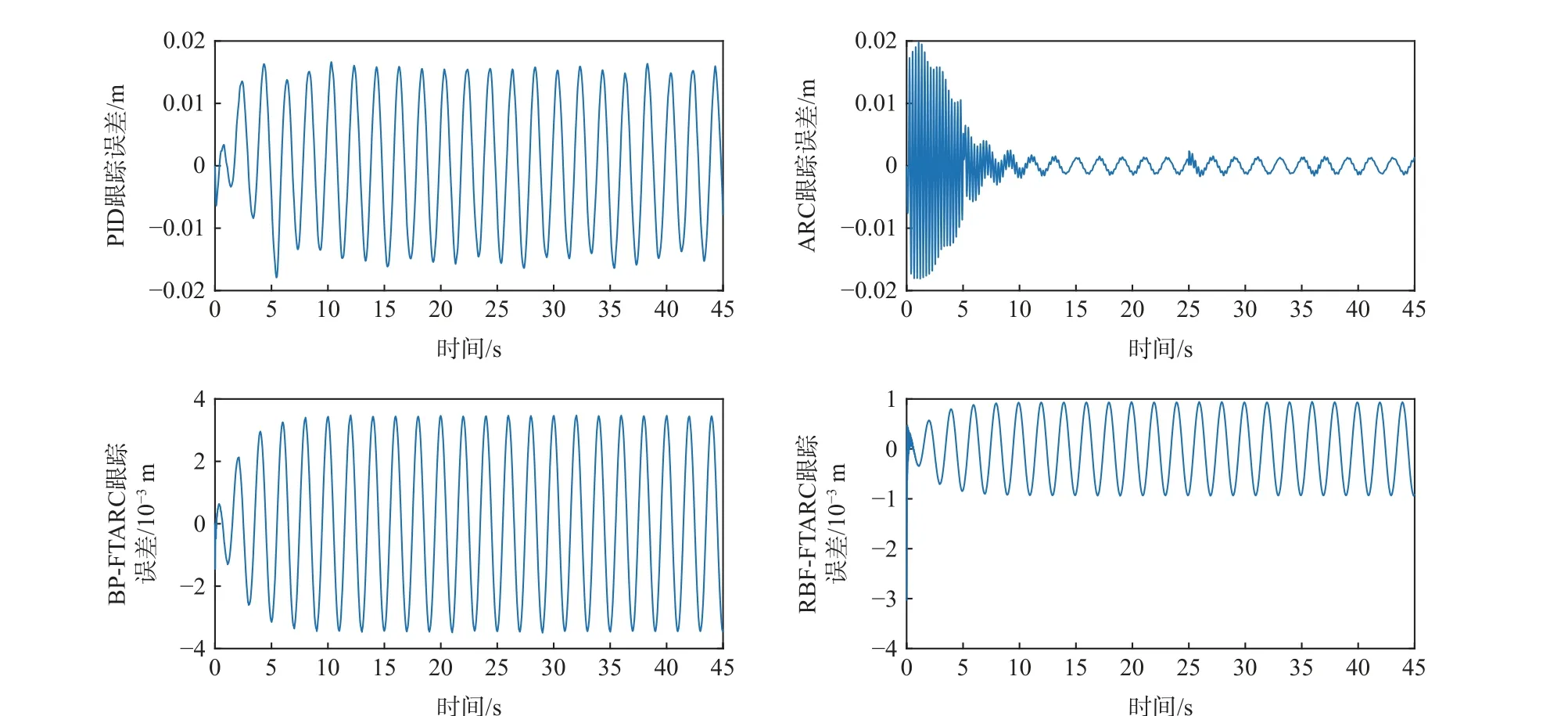
图14 工况3 下各控制器跟踪误差Fig.14 Tracking error of each controller under internal leakage condition

对比图14、表5 和图12、表3 可见，在工况3 下，系统受内泄漏故障的影响，工作条件比理想工况1 明显恶劣，此时4 种控制器的平均跟踪误差均比理想工况1 条件下有所增大；尽管工况3 更为恶劣，4 种控制器性能指标均有下降，但是由于本文设计的RBF-FTARC 在设计采用了状态观测器、故障补偿项、鲁棒项等措施，性能指标为4 种控制器中最优，跟踪精度比ARC 控制器提高一个数量级。

4）工况4。液压油的弹性模量受环境中的温度、湿度变化及油液污染的影响较大，特别是系统中混入空气造成油液污染之后，会引起油液弹性模量的异常变化。针对油液弹性模量异常变化的问题，设计工况4，跟踪高频的正弦位置曲线x1d=0.05+0.02sin(0.5πt)(1−e−0.5t)。其中，包含油液污染故障，受污染油液的弹性模量减小为1 200 MPa。

给定曲线及各控制器跟踪误差如图15 所示，各控制器性能指标如表6 所示。

表6 工况4 下各控制器性能指标Table 6 Performance index of each controller under condition 3

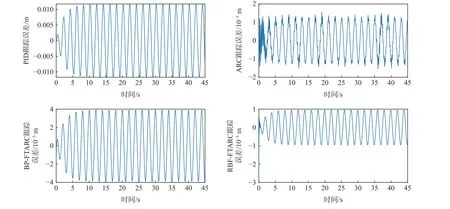
图15 工况4 下各控制器跟踪误差Fig.15 Tracking error of each controller under oil contamination condition

对比图15、表6 和图12、表3 可见，在工况4下，系统受油液污染故障的影响，工作条件比理想工况1 明显恶劣，此时4 种控制器的平均跟踪误差均比理想工况1 条件下有所增大；尽管工况4 更为恶劣，4 种控制器性能指标均有下降，但是由于本文设计的RBF-FTARC 在设计采用了状态观测器、故障补偿项、鲁棒项等措施，性能指标为4 种控制器中最优，跟踪精度比ARC 控制器提高约20%，比PID 提高约一个数量级。

7 结 论

1）针对系统中存在的非线性项，本文所设计的RBF 神经网络能够予以逼近。

2）针对系统中存在的和参数不确定性，所设计的参数自适应率能够逼近真实参数。

3）设计的鲁棒观测器能够获得系统内部状态和故障状态信息。

4）在控制器设计时对上述项予以补偿，李雅普诺夫函数证明所设计控制器有界稳定。

5）联合仿真结果表明，本文提出的RBF-FTARC与PID、ARC、BP-FTARC 相比，跟踪精度更高，且恶劣工况下对油液污染、油缸内泄漏、管路堵塞等故障有更好的鲁棒性。