锚定板位移-荷载关系近似解析算法

马 越，刘 杰

（湖南工业大学 土木工程学院，湖南 株洲 412007）

1 研究背景

锚定板结构是我国铁路部门首创的一种新型支挡结构形式。它发展于20 世纪70 年代初期，因具有较大的抗拔力而被广泛应用于立交桥台、边坡支挡、坡脚防护等工程中。具有造价低、形式简单、适用性广，适应能力强等优点。同时，很容易与其它挡土结构组合而创新出新的支挡结构形式。

锚定板按设置方向可分为水平、竖向及倾斜锚定板。本研究中将以竖向锚定板为例进行研究，它常被应用在挡土结构中，其工作机理是利用竖向锚定板提供的水平抗拔承载力，抵抗作用于支挡结构上的主动土压力，从而保持墙后土体平衡及稳定[1]。国内外大多数学者主要围绕锚定板抗拔承载力展开理论及试验研究。而锚定板的抗拔承载力及位移是这类支挡结构中必须确定的两个重要指标，但抗拔承载力及位移关系的研究却少有报道。

A．Ghaly 等[2]采用小比例室内模型试验研究了锚定板的抗拔机理及抗拔承载力影响因素。E. A.Dickin[3]采用离心机试验研究了锚定板的抗拔机理及抗拔承载力影响因素。丁佩民等[4]对砂土中模型锚板的抗拔试验数据、相关现场和模型试验结果进行了统计分析，阐明了模型试验和现场试验的锚板抗拔性能差异。朱碧堂等[5]基于砂土中锚锭板试验结果、黏土中锚锭板有限单元上下限解结果和试验资料的整理及统计分析，提出了锚锭板极限拉拔荷载表达式及相应参数的取值范围。刘建起[6]基于弹性地基梁法理论探讨了锚定板位移及相关参数计算的确定方法。何思明等[7]基于Mindlin 应力解，提出了采用修正分层总和法计算埋深锚板变形的新方法。

综上所述，前人的研究大多注重于锚定板的极限抗拔承载力，而对锚定板位移-荷载关系的分析方法及位移特性研究不系统和深入。而锚定板位移-荷载关系的数学表达式是有效而全面反映锚定板承载变形特性的主要形式，且较易被一般工程技术人员接受和掌握。目前，在工程实践中，板桩式挡土结构的设计大多采用竖向弹性地基梁法进行设计计算[8]，理论分析及工程实践结果表明：锚定板位移对挡土结构内力影响明显， 特别是对于刚度较大的支挡结构。然而在工程实际中，锚定板产生20～50 mm 的位移是十分正常的。因此，锚定板位移-荷载关系及位移特性研究就显得十分重要了。

本文拟以竖向埋设的锚定板水平抗拔力-位移关系为研究对象，建立锚定板与土相互作用的力学模型，提出锚定板位移-荷载关系的理论分析方法。然后，将理论分析结果与锚定板水平抗拔力-位移关系的Flac3D 数值模拟结果进行拟合分析，获得锚定板位移-荷载关系近似解析算式中的两个拟合参数。最后，将锚定板位移-荷载关系的理论分析结果与锚定板现场抗拔力试验结果进行对比，以验证本文所提出分析方法的可行性及合理性。

2 锚定板荷载-位移关系理论分析

2.1 基本假定

1）不考虑拉杆与土之间的黏着力和摩擦阻力，假定锚定板绝对刚性。

2）将锚定板视为竖向设置的弹性地基梁，设基床系数在地面处为0，且沿深度成线性增加。土体抗力采用“m”法计算，则锚定板前方土体基床系数为

式中：m为锚定板前方土体基床系数的比例系数，kN/m4；y为计算点的深度，m。

3）课题组对本地区典型的粉质黏土进行系列室内试验发现，锚定板前方土基床系数的比例系数m不是常数，而是与锚定板水平位移近似成幂函数关系。为此，根据《建筑基坑支护技术规程》中建议土的基床系数比例系数m与土的黏聚力及内摩擦角关系式[9]，并考虑锚定板水平位移对基床系数的比例系数m的影响，假定锚定板前方土体基床系数的比例系数与锚定板水平位移的关系为

式中：x为锚定板水平位移，m；φ为土的内摩擦角，°；c为土的黏聚力，kPa；k1、n为回归参数。

2.2 理论分析方法

锚定板在拉力P1作用下其力学模型及所建坐标系如图1 所示。

图1 锚定板力学模型Fig. 1 Mechanical model of anchor plates

假设锚定板的水平位移为x（m），转角为φ（°），则地面以下深度y处，锚定板前方土体对锚定板单位面积抗力为

式中：H为锚定板埋深，m；h为锚定板高度，m。

由水平方向力的平衡条件及以坐标原点O为矩心的力矩平衡条件可得：

联立式（2）与（4），整理可得锚定板荷载与位移的关系式为

式中：b为锚定板宽度，m；P1为钢拉杆所受的轴向拉力，kN；其中

由轴向拉伸与压缩的胡克定律，可得如图1 所示锚头处的位移为

式中：L1为钢拉杆有效长度，m；E为钢拉杆的弹性模量，MPa；S为钢拉杆横截面面积，m2。

在回归参数k1、n及相关计算参数均已确定的条件下，联立式（5）和（7），可求得锚定板锚头处的位移和拉力，从而获得锚定板所受拉力与锚头位移的关系曲线。

3 数值模拟及回归参数k1、n 确定

3.1 数值模拟

为确定前面已获得的锚定板抗拔力-位移关系式（5）中的两个参数，同时，探讨锚定板尺寸对m值的影响，采用有限差分软件Flac3D 对6 块不同尺寸的锚定板抗拔力-位移关系式进行数值模拟。为便于对比，且确保数值模拟结果与后期室内模型试验结果相对应，设定数值模拟模型尺寸为长×宽×高=5.0 m×5.0 m×3.0 m。锚板绝对刚性，采用shell单元模拟；锚杆表面绝对光滑，考虑到锚杆仅为传力构件，在数值模拟时，将作用在拉杆上的荷载直接施加在锚板中心点，如图2 所示。

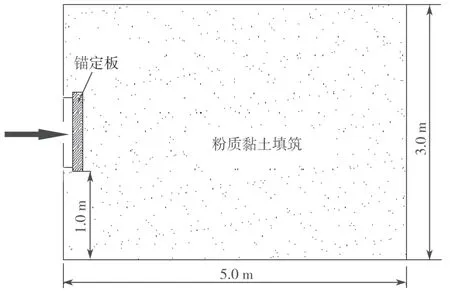
图2 数值模拟示意图Fig. 2 Numerical simulation schematic diagram

深埋在2.0 m 处1# ～ 6#的6 块正方形锚定板的边长分别0.5, 0.6, 0.7, 0.8, 0.9, 1.0 m。数值模拟相关参数如表1 所示。

表1 数值模拟参数Table 1 Numerical simulation parameters

6 个锚定板抗拔力-位移关系的数值模拟结果如图3 所示。

图3 1# ～ 6#锚板抗拔力-位移曲线图Fig. 3 Pulling force-displacement curves of 1# ～ 6# anchor plates

3.2 回归参数k1、n 确定

为确定锚定板抗拔力-位移关系式（5）中两个参数。将式（5）作为拟合公式对1# ～ 6#锚定板的数值模拟结果进行拟合分析。拟合曲线及两个参数的拟合结果如图4 a～f 及表2 所示。

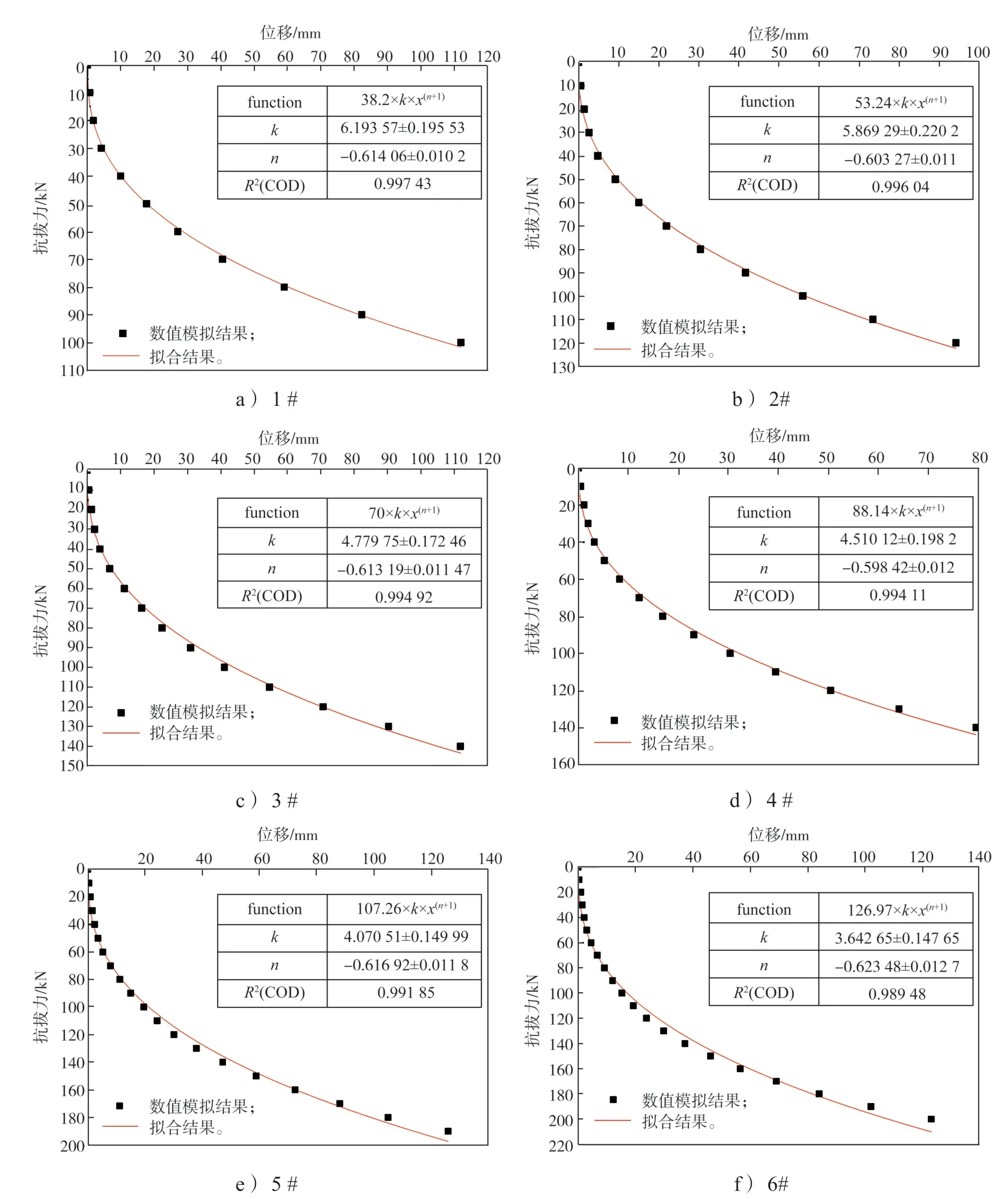
图4 不同型号锚板数值模拟与拟合结果对比曲线Fig. 4 Numerical simulation and fitting comparison curves of different types of anchor plates

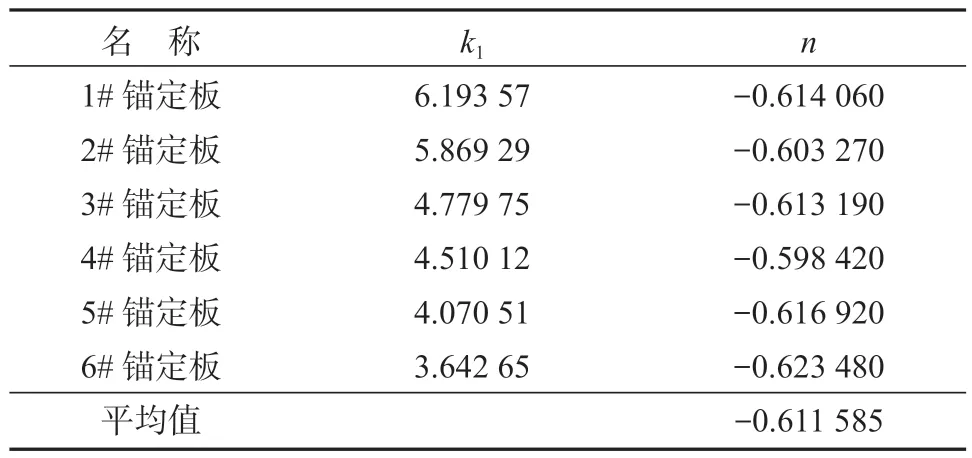
表2 回归参数k1、nTable 2 Regression parameters k1、n

图4a～f 中，R2是回归值与观测值的拟合程度，称为拟合集优度，其最大值为1，R2的值越接近1，说明回归值与观测值的拟合度越好；反之，R2的值越小，说明回归值与观测值的拟合度越差。

图4a～f 分别为1# ～ 6#锚定板位移-荷载关系拟合对比曲线。由图可看出，拟合集优度R2均在0.99左右。这说明拟合结果与数值模拟结果非常吻合，因此，对于尺寸不同的锚定板采用式（5）来分析锚定板抗拔力-位移关系是可行和合理的。

由表2 可知， 6 个模型试验结果获得的回归参数n相差不大，但另一个回归参数k1有较大差异。这说明锚定板尺寸对回归参数n的影响非常微小，而对回归参数k1的影响较大。因此，回归参数n可不考虑锚板尺寸的影响，而采用6 个模型试验结果获得的回归参数的平均值可作为理论分析的计算参数。

将数值模拟中的1#锚定板为基准板，其回归系数k1用ks的函数表示。参照文献[10]中的地基基床系数与基准板及承载板尺寸的关系式，假设回归参数k1与基准板回归系数ks及锚板尺寸的关系式为

式中ks=6.193 57。

基于表1 中2# ～ 6#锚定板的参数k1，通过式（8）进行拟合分析，获得拟合参数λ=1.63 拟合曲线如图5 所示。

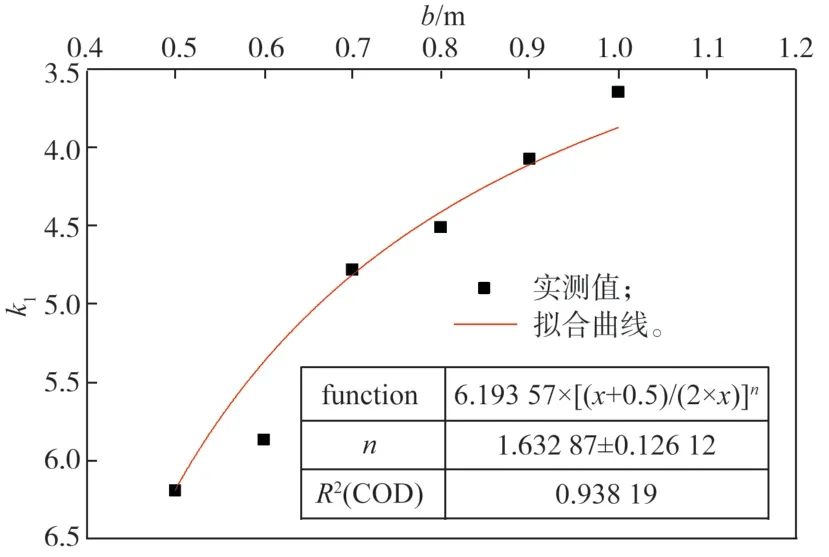
图5 k1 拟合对比曲线Fig. 5 k1 fitting comparison curve

由图5 可看出：拟合集优度R2为0.94。这说明拟合结果较好。因此，通过基准板的参数ks，采用式（8）确定其它尺寸锚定板抗拔力-位移关系式（5）中的参数k1是可行的。

4 土的黏聚力及内摩擦角对锚定板承载性状的影响

假设一锚定板尺寸为 1.0 m×1.0 m，埋设深度为5.0 m，土的重度γ=19.7 kN/m3。图6a 为土的内摩擦角φ=20°，土的黏聚力c从10 kPa 增加至40 kPa 时，锚定板抗拔力-位移关系曲线。图6b 为土的黏聚力c=20 kPa，土的内摩擦角φ从20°增加至40°时，锚定板抗拔力-位移关系曲线。由图6a、图6b 中可以看出，锚板的抗拔力随土的内摩擦角或土的黏聚力的增加而增加，但锚板抗拔力随土的内摩擦角增加而增加的幅度比随土的黏聚力增加而增加的幅度明显要大。因此，提高土的内摩擦角比提高土的黏聚力对提高锚定板抗拔承载力更有效。

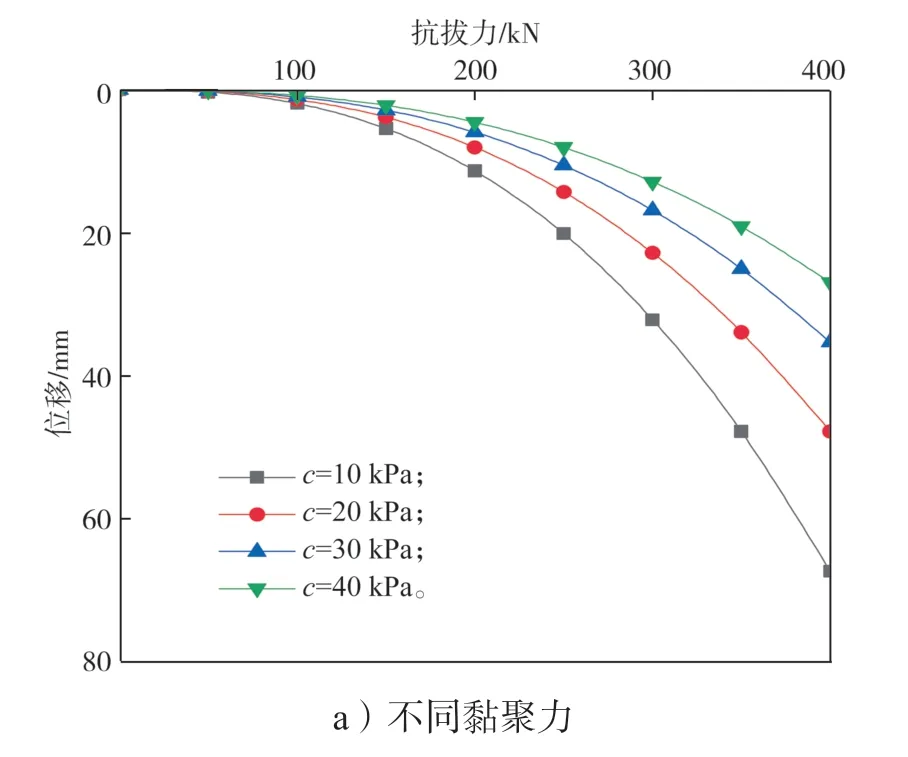
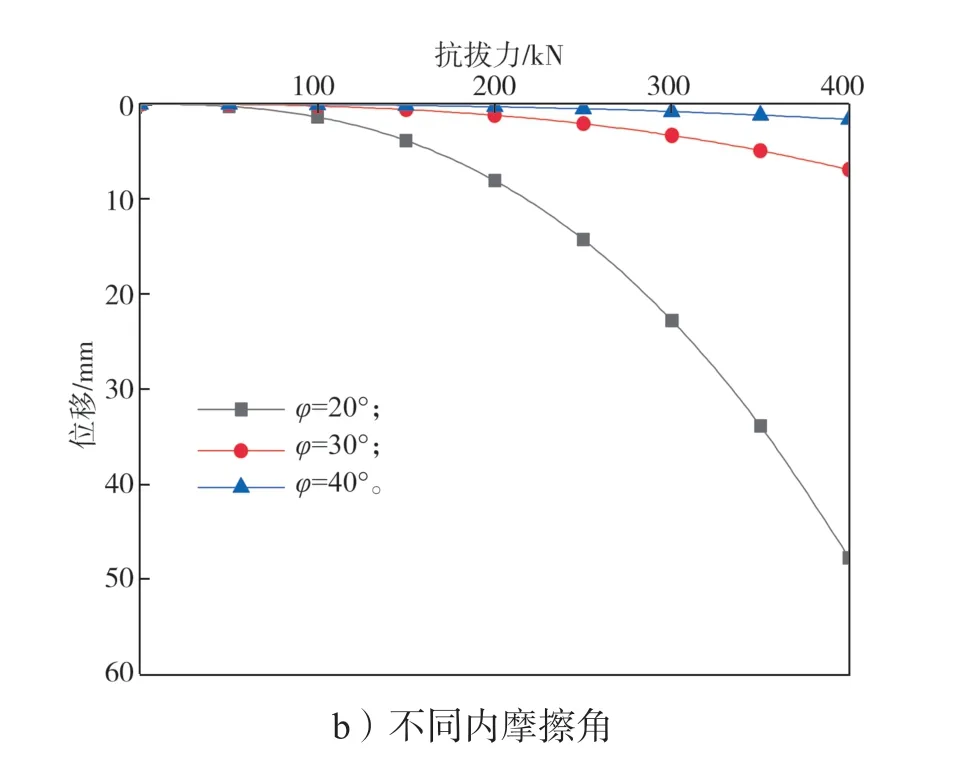
图6 不同黏聚力与内摩擦角的P-S 曲线Fig. 6 P-S curves of different cohesion and internal friction angles

5 算例验证

为了验证本研究中所提出的锚定板位移与荷载关系的理论分析方法的可行性，进行算例验证，并将理论分析结果与现场试验结果[11]进行对比。一块承受水平抗拔力的方形钢筋混凝土锚定板，埋设在压实粉质黏土中，锚定板几何尺寸为1.0 m×1.0 m，埋设深度为4.9 m，拉杆为3Φ25 螺纹钢筋，拉杆长度为14 m。锚定板抗拔承载力现场试验张拉设备为600 kN 油压张拉千斤顶。文献[11]给出的压实粉质黏土的内摩擦角φ=22.36°，黏聚力c=10 kPa，天然重度γ=19.8 kN/m3。采用上述土工参数，由式（5）获得的锚定板位移与荷载关系的理论计算结果与文献[11]给出的现场试验结果的对比曲线如图7 所示。由图7 可看出，采用本文建立的理论分析方法获得的计算结果与文献[11]给出的现场试验结果较为接近。这说明采用本文所建立的理论分析方法来分析锚定板位移与荷载关系是可行的。

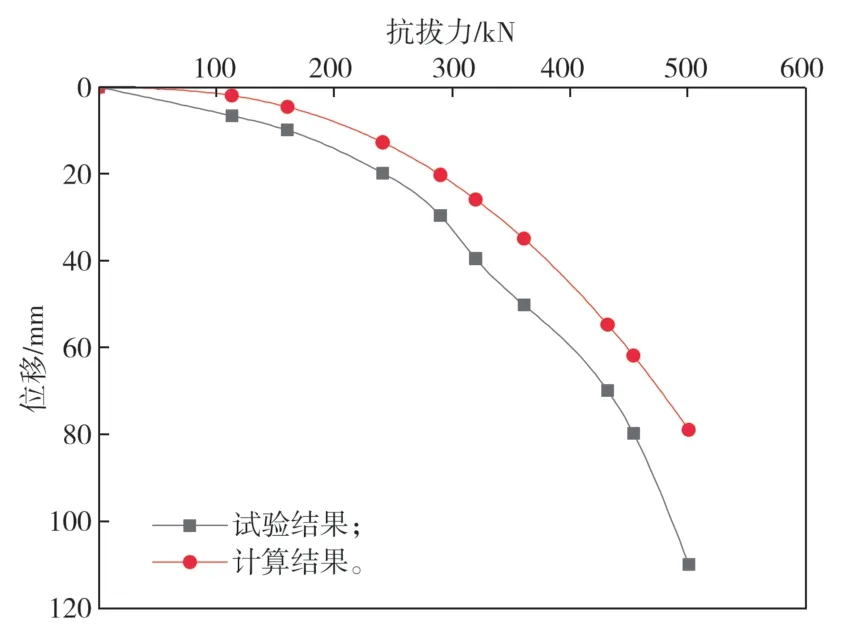
图7 锚定板位移-荷载关系曲线Fig. 7 Displacement-load relationship of anchor plates

6 结语

本文以竖向设置的锚定板为研究对象，首先基于弹性地基梁理论，建立锚定板位移-荷载关系及土体水平向基床系数的比例系数与锚定板水平位移关系的近似解析算式。然后，将理论分析结果与锚定板水平抗拔力-位移关系的Flac3D 数值模拟结果进行拟合分析，获得锚定板位移-荷载关系近似解析算式中的两个拟合参数。锚定板位移-荷载关系的现场抗拔力试验结果与理论分析结果验证了本文所提出的分析方法的可行性及合理性。

本文方法一方面为锚定板设计实现位移及承载力双重控制奠定了理论基础。另一方面，针对工程实践中锚定板的常规埋设深度，无须再人为区分深埋和浅埋来确定锚定板极限抗拔承载力，也不涉及机动场渐进发挥的特征，较容易被一般工程技术人员理解和接受。对实现锚定板支挡结构的初步设计有重要的指导意义。

本文对锚定板前方土体抗力沿深度的变化完全采用了“m”法。对锚定板埋设在某一深度范围内，水平变形系数和土体抗力随深度线性增加，可以认为是合理的。但当埋深超过一定深度后，土体抗力线性增加的假定显然不成立。目前仍不清楚这个深度的范围，以及当超过此深度后，土体抗力如何变化等问题，还有待于进一步研究。