非等温平行流下吹吸式通风系统流场的数值模拟

王 寅，赵福云, ，唐宇飞，文雅冰

（1. 武汉大学 动力与机械学院，湖北 武汉 430072；2. 湖南工业大学 土木工程学院，湖南 株洲 412007）

0 引言

21 世纪来，随着“中国制造2025”与德国“工业4.0”[1]概念的提出，我国工业建筑数量不断增加，而工业场所会排放出各种污染物，包括有毒有害气态污染物和颗粒物等。因此工业建筑室内环境问题也引发研究者的关注，如何有效控制污染物扩散成为学者研究重点[2-3]。吹吸式通风系统作为常用的局部通风方式，主要结合吹吸气流实现污染处理目标，是一种高效通风方式，对室内污染物清除有很大优势。

目前有关室内有障碍物吹吸式通风的讨论较多，在理论与模拟方面，孙一坚[4]对气流罩合成理论进行分析，得出了不同参数设置下吹吸气流特性。于航等[5]通过微积分进行分析，确定吹吸气流动量变化情况，所得结果对明确吹吸气流流场特性有重要意义。林爱晖[6]应用CFD（computational fluid dynamics）模拟了卸料斗中气相及气固两相流场，总结含尘气流流动特性，指出双侧吹吸通风能有效控制粉尘扩散。马骏驰[7]研究了非等温条件下吹吸式通风系统中流场和污染物的分布规律。实验研究中，付海明等[8]建立了缩比例模型，分析模拟烟雾发生器污染气流对粉尘等颗粒污染物的影响，通过调整风量、模型尺寸讨论吹吸气流对流场结构影响的最佳参数。Ojima J.等[9]在吹吸式通风系统流场内设置了人体模型，分析得出捕集效率不会发生显著变化。Zhou Y.等[10]研究发现人体对该系统吸收污染物影响较小。对比文献[9-10]和美国政府工业卫生家协会（ACGIH）的实验可知，对该系统吸收污染物影响显著的是风口尺寸。同时障碍物后形成的涡流区与污染物扩散有较大影响。R. T. Hughes[11]发现障碍物在射流区域2/3 后，相应影响明显降低，通风系统清除性能也受到影响。

上述研究表明，在内有障碍物的吹吸式系统中，送风射流特性对流场有着显著影响。本文拟基于非等温射流情形下，分析吹吸式通风系统内存在障碍物的流场以及清除污染物性能的情况，以期为吹吸式通风系统优化设计提供参考。

1 数值计算模型

1.1 物理模型

本文模型为一个简化的三维单体房间，参照文献[12]建立物理模型，如图1 所示。

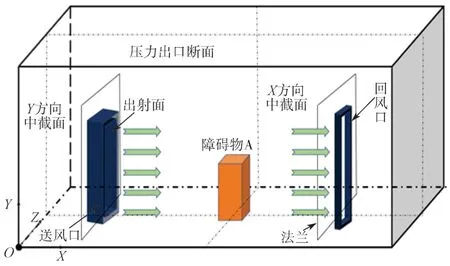
图1 三维吹吸式通风系统示意图Fig.1 Schematic diagram of the three-dimensional blow-suction ventilation system

实验室尺寸为长5.64 m、宽14.01 m、高3.27 m。按照通风系统数值模拟方式，通风系统设置在离墙面（Y=0）3 m 处，为进行补风，在距离通风系统5.64 m 处的外墙上设置单独一个窗口，尺寸为0.75 m×1 m。整个房间门窗全部保持关闭状态。在模拟时由于小窗补风气流比较微弱，故简化处理时忽略其影响。设置坐标原点为顶点的O点。吹风口、排风口上下均设置了挡板，其宽度为2.0 m、长度为1.5 m，吹风口尺寸和排风口尺寸均为0.50 m×0.96 m×0.96 m。吹排风口间距3.8 m。吹排风口沿X轴间距3.8 m。同时，在吹排风口轴线中心的位置有一障碍物A，模型尺寸为0.64 m×0.64 m×0.64 m。

1.2 数学模型

吹吸式通风气流流场为三维湍流场，基于三大守恒方程确定控制方程。研究过程中，为更好地满足量化分析要求，需对流体进行如下计算分析：

RNGk–ε模型的湍流动能k和耗散率ε的方程为

式（4）～（5）中：v为运动黏度系数；vt为湍流动力扩散系数；σk和σε为湍流普朗特数；Pk和Gb分别为由惯性风作用和热浮升力引起的湍流动能源项；C1ε、C2ε、C3ε为经验常数，其中，C1ε=1.42，C2ε=1.68，C3ε=1.0。

用阿基米德数Ar[13]衡量温度差对流体的影响，其计算公式如下：

式中：g为重力加速度，m/s2；do为当量直径，m；Ts为射流出口温度，K；Te为环境空气温度，K；u1为射流出口速度，m/s。

1.3 计算域与网格划分

计算域整体尺寸为0.64 m×7.00 m×3.27 m，送风口出射断面设为入口速度边界（inlet），出风口设置为出口边界（outlet），与Y轴垂直的两个面设置为压力边界其余面边界，设置为无滑移固体壁面边界且设为定壁温。考虑模拟对颗粒轨迹的计算将受湍流的随机性影响，本模拟设置的颗粒性质为MgCO3，粒径为1.5×10-5m，颗粒受湍流的影响较小。运动速度和入口风速一致。对于网格划分，将三维吹吸式通风系统划分为规则四边形网格，而排风口周边形状不规则。选择单元网格Tex/Hybird，运用此类型网格对整个计算区域进行划分，分别为40 万、50 万、60万和70 万。为了验证网格无关性，检验其独立性，在非等温工况下对比吹吸式流场轴心速度曲线，轴心速度在不同网格数下的变化趋势如图2 所示。

图2 各网格数下的无量纲速度分布图Fig. 2 Non-dimensional velocity distribution diagram for each grid number

由图2 的对比结果可知，40 万、50 万、60 万网格的无量纲速度趋势基本一样，而70 万偏差较大，考虑计算准确可靠性和计算时间成本，将网格数量设置为60 万最佳。

2 模型验证

为了验证非等温工况下本通风系统数值模拟的准确性和可靠性，将RNGk-ε湍流模型的模拟计算结果与文献[14]的实验结果进行比较，其比较具体的测点分布如图3 所示。

图3 实验测点分布图Fig. 3 Distribution map of experimental points

实验室规模大小为11.3 m×7.1 m×3.3 m，吹风口尺寸为0.5 m×0.5 m，风口与墙体间隔1 m。轴心测点沿着X轴方向，设置测点间隔0.4 m，测量轴心流速；Z轴上设置监测点，用于测量X截面上系统运行的最大速度。实验通过送风口控制送风温度为305.76 K，与室内空气温度293 K 形成温差。在吹风口前端布置3 kW 的电热丝加热升温，实际温度可达32.6 ℃，阿基米德数为0.024。实验工况具体参数如表1 所示。

表1 实验工况参数表Table 1 Test condition parameter table

将模拟结果与实验数值进行拟合，结果如图4 所示。A1为送风口尺寸，V为测点速度，V1为送风口速度，V2为排风口速度，Vmax为X截面上显示的最大速度，H为最大速度所对应的高度，x为横坐标，D为入风口到回风口距离，Tm为轴心温度，To为室内环境温度，T1为风口射流温度，无量纲温度。显然，数值模拟结果与实验结果变化趋势基本吻合，故本文采用的数值模型在非等温工况气流流动的模拟计算是可行的。

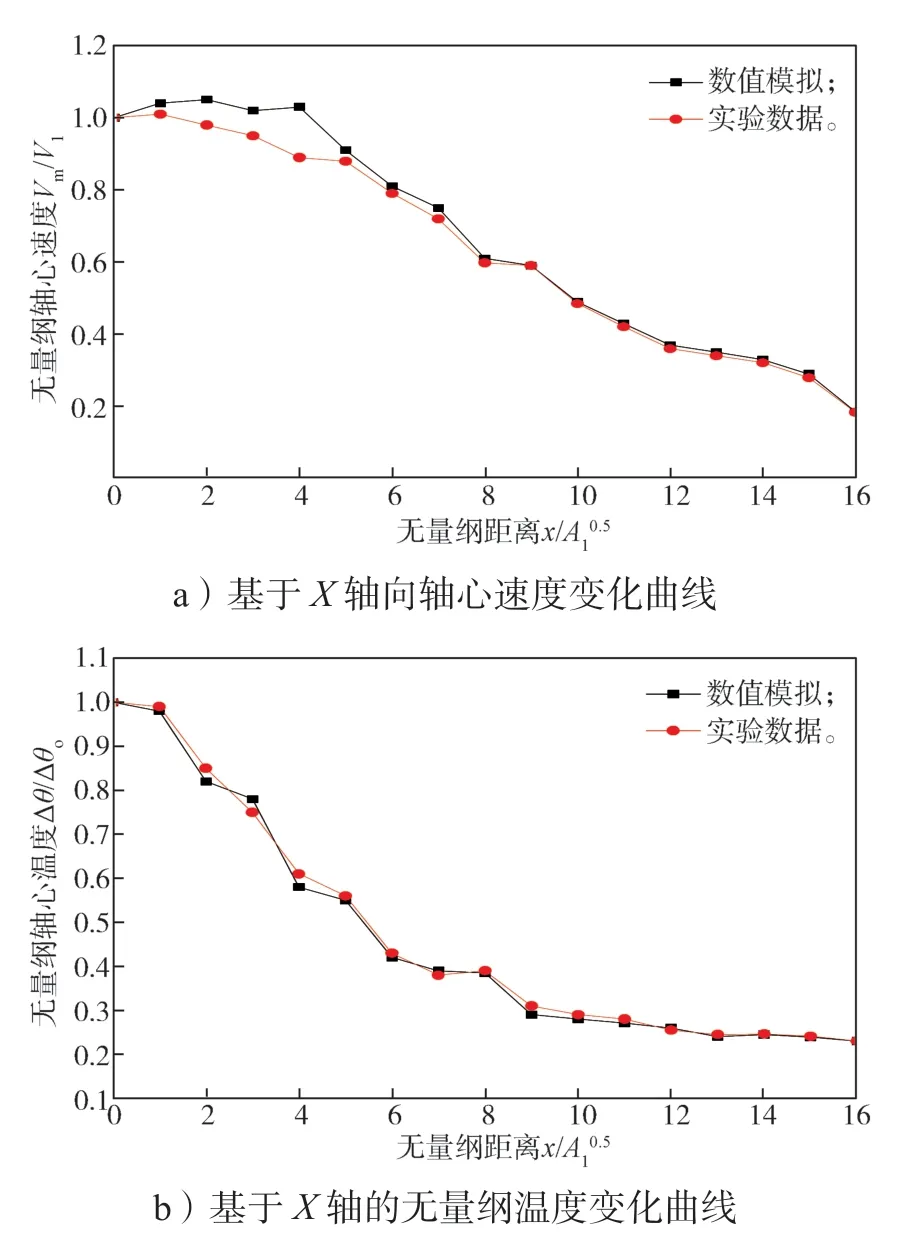
图4 数值模拟与实验结果对比Fig. 4 Comparison between numerical simulation and experimental results

3 结果与讨论

本文分析了吹吸式通风流场的基本特性，讨论两方面（一是不同送风温度，二是不同送风速度）条件下，对流场的轴心速度、温度分布、示踪粒子捕获效率以及涡流中心高度变化的基本规律。

3.1 不同送风温度下的吹吸式通风流场特性

3.1.1 送风温差工况设置

本文参考了文献[14]实验设置条件，设置送风速度为0.606 m/s，排风速度为2.07 m/s，以保持模拟与实验条件的一致性。而环境温度设置为293 K,轴心速度为Vm，送风温差采取等梯度（3 K）设置，分别设置为0, 3, -3, 6, -6, 9, -9, 12, -12, 15, 18 K 等11种工况，具体工况参数设置如表2 所示。

表2 变送风温差工况表Table 2 Working condition table of variable supply air temperature differences

3.1.2 轴心速度变化规律

由前面模型验证结果可知，在障碍物条件下，Case 5-0 轴心速度沿X方向是逐步递减的。当送风口之间间隔4.7 m，由于汇流场的影响，轴心速度加快。当射流温度高于室内环境温度时，从图5 可以发现，在送风温差在6 K 内，障碍物前侧速度变化放缓。然而当送风温差大于6 K 时，轴心速度缓缓增加，之后下降。当靠近排风口时，速度会先增大后减小，之后速度急剧增大至接近排风速度。在上升期，随着送风温度增大，轴心速度也增大。

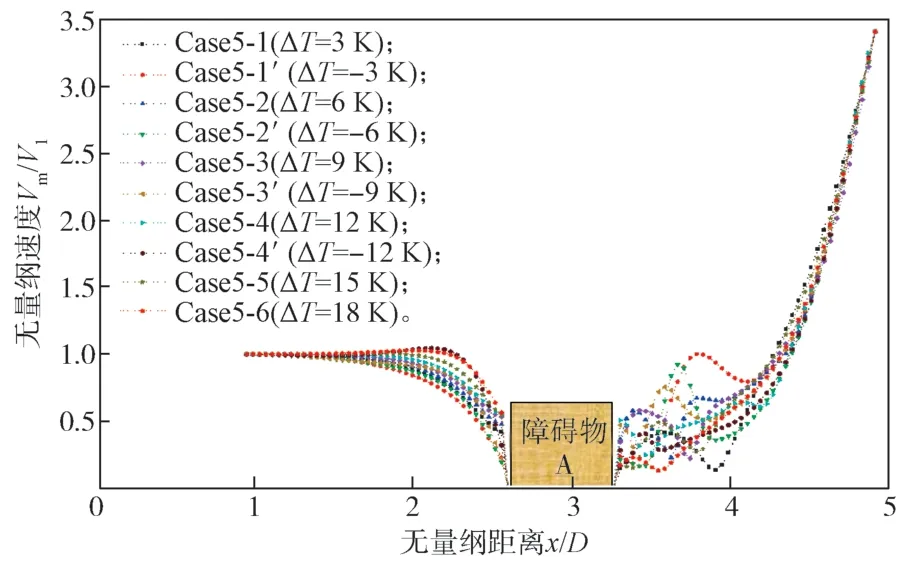
图5 各送风温差下的轴心速度-距离变化曲线Fig. 5 Axial velocity distance change curves with a temperature difference of variable air supply

3.1.3 轴心温度变化规律

本文为了更清晰反映变化趋势，将轴心温度无量纲化，在多种送风温度下，轴心温度变化曲线见图6。

图6 各送风温差下的无量纲轴心温度-距离变化曲线Fig. 6 Non-dimensional axis temperature distance change curves under variable air supply temperature differences

从图6 中可看出，送风温度增大情形下，轴心无量纲温度会加快递减。当温差为3 K 时，无量纲温度在x/D=3.67 处开始递减，当温差达9 K 时，在x/D=3.47 处开始递减；温差增大到18 K 时，其衰减点提前到x/D=3.2。递减起点实质上和送风口的距离同时减小，轴心温度沿着吹吸流场方向加快下降。

3.1.4 回流区涡流中心高度变化规律

为了研究回流区涡流中心向上偏移程度随送风温度的变化情形，对污染物累积的程度进行分析，主要讨论Y=3.5 m 截面上的流体分离，涡流中心不同温差条件下的偏移高度如图7 所示。可以看出，在吹吸式流场内，当送风温度增大，涡流中心偏移高度呈现类似周期性的先增大再减小，虽然涡流中心不断升高，但基本维持1.1 m 左右。

图7 各温度差下的回流区涡流中心偏移高度Fig. 7 Vortex center offset height in the recirculation zone under different temperature differences

3.1.5 捕集效率

本文在进行模拟时，假设对应的颗粒物为示踪粒子，这种粒子的跟随性高，计算分析并确定出排风口粒子数及比值，并计算出捕集效率η。

定义捕集效率η的表达式如下：

式中：m为排风口捕获到的粒子数；n为吹风口释放的粒子数。

即在吹风口加入的示踪粒子，在不断流动过程中，其中一部分进入排气罩，有的则逃逸，然后模拟分析确定出排出的粒子数与释放的粒子数之比，就可实现计算效率的目的。

引入示踪粒子捕集效率这一指标，对比送风温差扩大对示踪粒子实际进入排风罩所占比例。如图8所示，在非等温射流情形下，送风温差改变对示踪粒子捕集效率有着显著影响。在工况5-0（ΔT=0 K）下，示踪粒子捕集效率达91.07%。温差增大到3 K时，捕集效率增大到95.09%，当送风温差继续增大，捕集效率反而降低。随着温差继续加大，捕集效率持续降低。这是由于送风温度增大，阿基米德数Ar增大，热浮升力加强，射流整体向上偏移。而过高的温度导致偏移过大，流体不能被排风口流场引导，引起示踪粒子逃逸。然而，当降温送风时，阿基米德数Ar减小，气流汇聚在障碍物之前，从而减小示踪粒子的捕集效率。因此，适当调整送风温度或者与环境温度趋于一致时，污染物的捕集效率会较高，降低污染物逃逸能力。

图8 不同送风温差下的示踪粒子捕集效率Fig. 8 Tracing efficiency of tracer particles under different supply air temperature differences

3.2 不同送风速度下的吹吸式通风流场特性

3.2.1 送风速度工况设置

在升温送风状态下阿基米德数对污染物捕集效率影响显著。在上述讨论中，保持送风温差为9 K，排风速度V2为2.07 m/s 时，污染物捕集效率仅为38.84%，具有较大余量可供优化分析。送风速度采用等梯度（0.3 m/s）设置，改变送风速度V1，设置6种等区间工况进行模拟。环境温度保持To=293 K，不同送风速度工况如表3 所示。

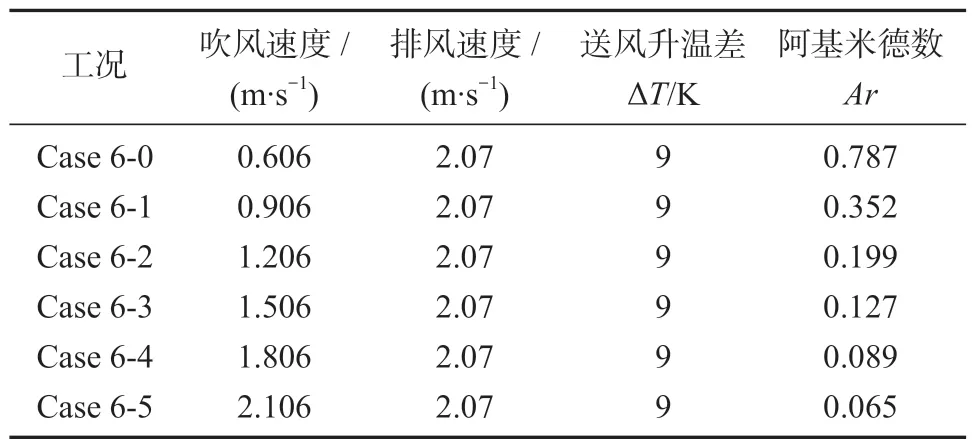
表3 各送风速度下的工况Table 3 Working conditions under variable air supply speeds

3.2.2 轴心速度变化规律

图9 为各送风速度之下轴心速度变化曲线。如图9 所示，射流速度的改变对轴心速度影响显著，对于工况6-0（V1=0.606 m/s）来说，风速较低，流体受热浮升力与惯性力双重影响，随着距离x增大，轴心速度先增大后减小。当增大送风起始速度，降低热浮升力与惯性力比例，随着距离增大，轴心速度下降缓慢。随着送风速度继续增大，在射流范围内轴心速度下降得更加显著，也就是说送风速度增大，射流控制的区域范围将会增加。当达到障碍物之后，距离的增大轴心速度受排风口射流速度的影响更加显著。

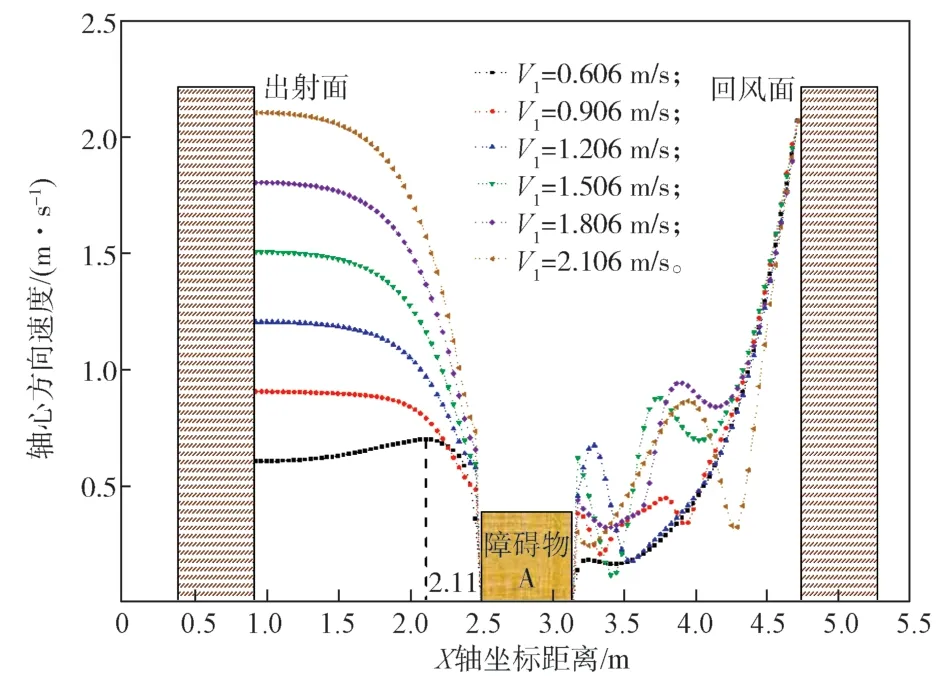
图9 各送风速度下的轴心速度变化曲线Fig. 9 Axis speed change curves under variable air supply speeds

3.2.3 轴心温度变化规律

图10 为各初速度下轴心温度变化曲线。从图10的变化曲线中可以看出，在送风速度较低时，空气受热浮升力的影响较大，障碍物A 后的空气受扰动较小，轴心温度更接近环境空气温度。随着送风速度增大，风压产生的惯性力随之增强，轴心温度出现先增后减的情形，且速度越大，温度衰减的起点越延后。然而，当送风速度增大到1.806 m/s 时，温度衰减点为x/D=3.9。随着风速继续增大，温度衰减缓慢，这是因为速度增大，Ar反而减小，在惯性力的主导作用下，气流维持水平流动。

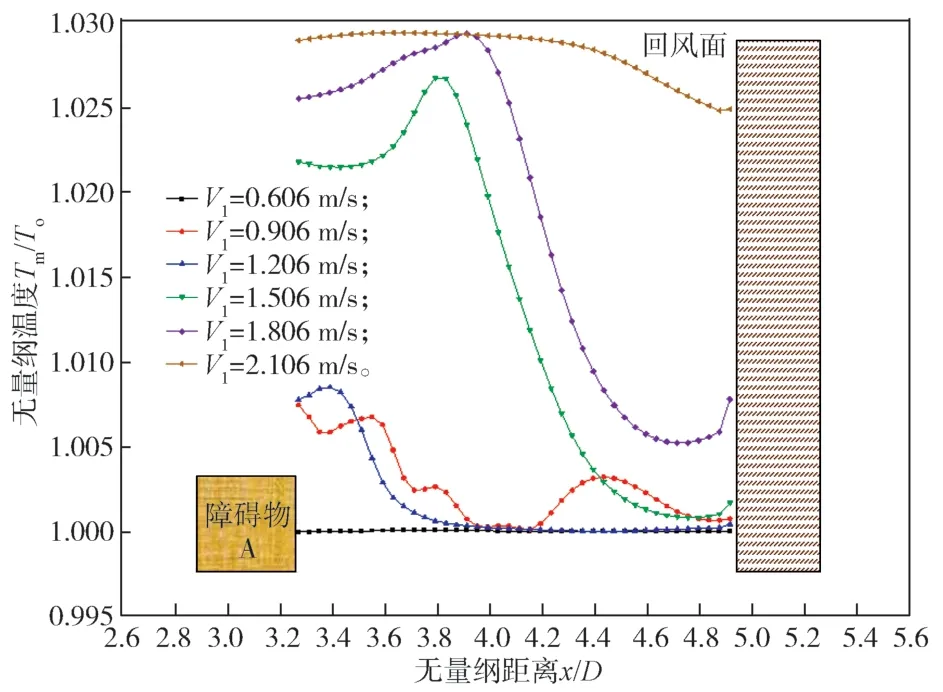
图10 各初始速度下的轴心温度变化曲线Fig. 10 Axle temperature change curves under each initial speed

3.2.4 回流区涡流中心高度变化规律

图11 为各送风速度下回流区涡流中心偏移高度模拟结果。

图11 各送风速度下的回流区涡流中心偏移高度Fig.11 Vortex center offset height analysis in the recirculation zone under various air supply speeds

由图11 的结果可知，在吹吸式通风流场内，随着送风速度增大，回流区涡流中心涡流偏移高度呈现先增大后减小的趋势，向上偏移程度下降。由于送风速度增大即阿基米德数减小，涡流中心不断升高，然而基本维持在1.1 m 以下的范围。然而，送风速度越大，Ar数递减，热浮升力与惯性力的比值下降，即惯性力占主导地位。送风射流沿着平行轴线的方向流动，从而控制整个流场。

3.2.5 捕集效率

为了直观地反映出吹吸流场基于不同风速条件下对捕集效率带来的影响，将初始速度不同的工况进行比较，如图12 所示。

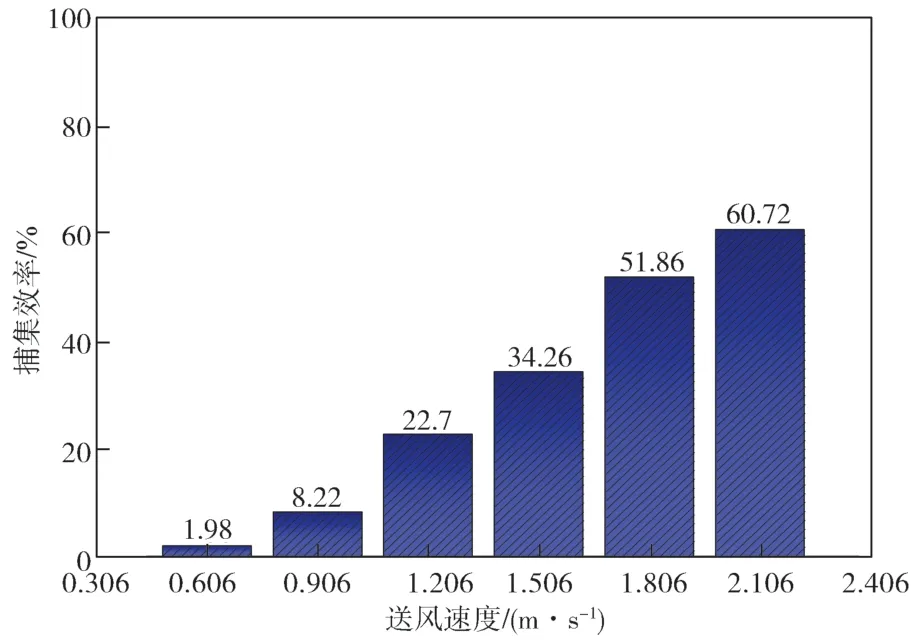
图12 各送风速度下吹吸流场针对污染物捕集效率产生的影响分析Fig. 12 Analysis of the influence of the blow-suction flow field on the pollutant capture efficiency under variable air supply speeds

从图12 中可以看出，对非等温吹吸式通风系统而言，送风速度的改变显著影响示踪粒子实际的吸收性能。捕集效率随着送风速度的增大而增大。当送风速度增大到1.806 m/s，捕集效率增大到51.86%。这是由于送风速度增大，阿基米德数Ar变小，即热浮升力相较于惯性力减弱，空气也渐渐地与轴线平行，送风射流能够将示踪粒子送到排风速度口中。故捕集效率随着送风增大， 即合理地增大风速来增大污染物的捕集效率是可行的。

4 结论

本文主要针对非等温射流条件下吹吸式通风系统流场规律进行了讨论，基于送风温差和送风速度，从轴心速度、温度分布、涡流结构以及示踪粒子的扩散等变化进行分析，主要有如下结论：1）采用RNGk-ε湍流模型模拟非等温射流条件下吹吸式通风系统流场，模拟结果与实验数据对比结果表明，两者的趋势基本一致，吻合较好。2）当射流与环境空气存在温差时，随着温差扩大，阿基米德数增大，轴心速度快速递减；轴心温度沿着吹吸流场方向加快下降。涡流中心偏移高度呈现出先增大后减小的趋势。而对于污染物扩散方面，当送风温差达6 K 时，即阿基米德数大于0.546，整个系统的捕集效率也显著降低；当送风温度接近环境温度时，整个系统的捕集效率较大，吹吸式系统吸收污染物的能力最强。3）当射流与环境空气温度一定时，扩大射流速度，即阿基米德数减小，射流沿着流场轴心运动，轴心温度先增大后减小，同时射流影响的区域范围将会增加，有利于提高捕集效率。射流形成的涡流中心向上偏移程度下降。对污染物清除而言，合理地增加送风速度对于吹吸式系统的污染物清除是有利的。