HPM视角下的“球的体积和表面积”教学

摘 要：HPM（即“数学史和数学教育”）的研究正成为一线教师研究的热点之一，数学史和数学文化在教学中的融入越来越受到人们的重视。如何利用数学史和数学文化促进数学教育成为人们研究的重要课题之一，很多教师和学者进行了不少HPM方面的研究，取得了令人瞩目的成果。然而，在HPM研究中高评价、低应用的现象普遍存在，很多教师在教学过程中存在着数学史材料的简单堆砌，忽视学生学情及对数学史材料的挖掘深度不够等问题。文章以“球的体积和表面积”的教学为例，以HPM的视角设计和实施“球的体积和表面积”的教学，以古人对圆和球的探究过程为主线，再现了古人对球的研究思想方法，让学生经历球的体积和表面积公式的探究历史，体会先哲的智慧，形成直观想象和逻辑推理等数学学科核心素养，实现全面发展。

关键词：HPM视角；牟合方盖；球的体积和表面积

中图分类号：G427                                文献标识码：A                                       文章编号：2097-1737（2023）06-0004-03

引  言

球是一种重要的几何体，是培养学生空间想象能力、空间思维能力和直观想象核心素养的重要载体。

《普通高中数学课程标准（2017年版2020年修订）》（以下简称《课程标准》）对“球的表面积和体积”的相关要求为：“知道球、棱柱、棱锥、棱台的表面积、体积的计算公式，能用公式解决简单的实际问题。”[1]人教A版教材对本节内容的处理比较简单，并未对球的体积公式进行推导证明，仅在阅读材料“探究和发现”中对祖暅原理，柱体和锥体的体积及球的体积公式的演绎推理过程进行了简单的介绍。笔者认为教师不应把本节课的教学目标仅仅停留在掌握球的体积公式、表面积公式及其简单的应用这样浅层的知识技能层面，可以充分利用数学史材料，以球的体积、表面积为知识载体，全面提升学生的数学学科核心素养和文化涵养，促进学生的深度学习和终身发展。

在本节课的教学中，笔者以《课程标准》为依据，以《中国高考评价体系》为导向，以教材为蓝本，以学生学情为出发点，从History and Pedagogy of Mathematics（数学史与数学教育，以下简称HPM）的视角设计和实施本节课的教学。本节课教学目标设定如下。

（1）了解中国古人对球的体积公式的探索过程，体会古人“以方套圆，化圆为方”的思想方法，感受先哲的智慧；

（2）经历球的体积和表面积公式的探索过程，了解其中蕴含的微积分思想方法；

（3）掌握球的体积和表面积公式，并能利用其解决简单的相关问题。

一、历史材料及其应用

（一）阿基米德墓碑问题

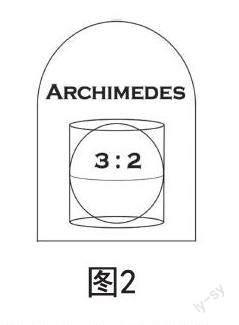
阿基米德（Archimedes）是古希腊伟大的数学家、物理学家，是静力学和流体力学的创始人。在阿基米德于公元前212年不幸被罗马士兵杀害后，马赛拉斯为他修建了一座颇为宏伟的陵墓，并在墓碑上镌刻了球内切于圆柱的图形，以此缅怀阿基米德在数学上的卓越贡献。

（二）刘辉与牟合方盖

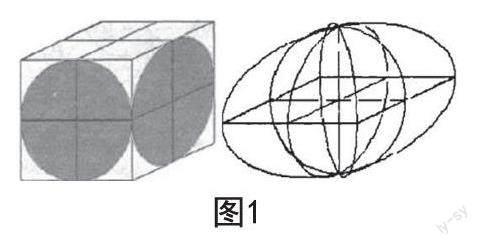
在《九章算术》“开立圆术”中有一段关于球的体积公式的记载，认为球的体积：圆柱的体积=圆柱的体积：正方体的体积=π∶4，（其中圆柱与正方体的各个面相切，球与圆柱体的底面与侧面相切）。刘辉认为这个求法不对，并构造了一个新的几何体——“牟合方盖”（如图1）。所谓“牟合方盖”，就是指由两个同样大小但轴心相互垂直的圆柱体相交而成的立体图形。

刘辉指出，牟合方盖与相应内切球的体积之比=4∶π，只要求出牟合方盖的体积就能计算出牟合方盖内切球的体积。刘辉虽然没能最终得出球的体积公式，但这为此后祖暅推导球体的体积公式提供了重要的思路。

（三）祖暅及球体积公式的推导

南北朝时期大数学家祖冲之的儿子祖暅在刘辉研究的基础上利用祖暅原理求得了八分之一牟合方盖与牟合方盖外接正方体八分之一差的体积，进而求出了牟合方盖的体积，推导出了球的体积公式。

二、教学设计与实施

（一）创设历史情境，自然引出球的体积和表面积

教师首先用PPT呈现图2，并对图形进行说明：图中球的表面积和体积都是圆柱体表面积和体积的，以此优美的数学结论激发学生的学习热情，使其感受数学的美；再通过对阿基米德的生平及墓碑来历的简介，进一步增强课堂的文化性和趣味性，有效激发学生的数学学习热情。

师：同学们，你们看这张图像什么？

生：……

师：这画的是一个墓碑，是古希腊伟大的数学家阿基米德的墓碑，人们为了缅怀其对数学学科的贡献，在其墓碑上鐫刻了这样一个图形。图中所表达的意思是：球的体积是圆柱体体积的，球的表面积也是圆柱表面积的，这节课我们就来论证一下这一结论。为了证明这一结论，我们需要先掌握球的体积和表面积计算公式。（此间向学生介绍阿基米德的生平及墓碑的来历）

（二）球的体积和表面积公式的推导

1.球的体积公式的推导

（1）中国古人对球的体积公式的探索

“化圆为方、以方探圆”是中国古人研究圆与球的重要思想。据《九章算术》“开立圆术”中的记载，中国古人认为球的体积∶圆柱的体积=圆柱的体积∶正方体的体积=π∶4，（其中圆柱与正方体的各个面相切，球与圆柱体的底面与侧面相切）。

（2）刘辉与牟合方盖

刘辉认为这个求法不对，他构造了一个新的几何体——“牟合方盖”，并指出牟合方盖内切球的体积∶牟合方盖的体积=π∶4，只要求出牟合方盖的体积，就能计算出球的体积。

（3）祖暅与球的体积公式的推导

引理1——祖暅原理：夹在两条平行平面间的两个几何体，被平行于这两个平面的任何一个平面所截，如果截面面积都相等，那么这两个几何体的体积相等[2]。

祖暅推导球的体积公式的思路沿袭了刘辉的思路，即求牟合方盖的体积。祖暅发现，八分之一牟合方盖与牟合方盖外接正方体八分之一所夹的部分与某四棱锥体积相同（如图3），故通过求出该四棱锥的体积，求出了牟合方盖的体积，进而推导出球的体积公式：V=πR3。

（4）几何模型的简化

我们还可以对推导球的体积公式的几何模型进行简化（如图4），由祖暅原理，我们不难得出底面半径为r，高为r的圆柱和与之同底等高的圆锥的体积之差等于半径为r的半球的体积。

进而可得球的体积公式：V=πR3。

2.球的表面积公式的推导

利用微积分的思想，将球面分为n块，记第i块的面积为Si，那么当n足够大的时候，我们就可以将球体看作n个椎体的组合，其中第i个椎体的底面积为Si，

高为R，其体积Vi=SiR，球体的体积等于：

V1+V2+……+Vn=R（S1+S2+……+Sn）=RS=πR3

所以，S=4πR2。

3.问题解决

例：如上图5，圆柱的底面直径与高都等于球的直径。

求证：（1）球的体积等于圆柱体积的；（2）球的表面积等于圆柱表面积的。

三、学生反馈

课后，我们以问卷调查、个别访谈和作业的形式，

就本节课的教学情况和教学效果向学生进行了调查研究。从学生课后反馈的信息来看，本节课很好地达成了预定的教学目标，学生能够独立思考完成课堂限时训练和课后巩固练习，优秀率达90%以上，从中反映出本节课知识技能方面的教学目标达成度很好。对于球的体积和表面积公式的探究历史，100%的学生表示已了解公式的探究历史。对于球的表面积和体积公式的推导过程，66.1%的学生表示理解，26.8%的学生表示基本理解，7.1%的学生表示还未理解公式的推导过程，主要问题集中于利用牟合方盖推导球的体积的过程。其中，92.8%的学生表示喜欢这样的数学课堂教学方式，认为数学文化和数学史的融入能够使数学课堂更加有趣、丰富，有助于他们理解、内化数学知识；也有7.2%的学生认为，数学文化和数学史的融入对其数学学习没有明显的帮助，数学文化和数学史的融入会占用一部分的课堂教学时间，导致其训练时间减少。

四、教师反思

在教学过程中，教师应结合具体教学内容和学生学情，合理地提炼数学史材料，使之发挥出最大的教学价值，而不能仅限于数学史材料的简单堆叠。

我们认为数学文化和数学史融入课堂教学过程应该注意以下几点。

（1）选取的数学史材料应在本节课教学中具有很大的教学价值和教育意义；

（2）数学文化和数学史的融入应自然、流畅，在数学史材料的应用过程中，教师需要考虑到知识发生发展的历史性和逻辑性以及学生的学情，需对数学史材料应用方式进行充分考量和恰当选择，必要时需对数学史材料进行适度加工处理，使之更适合课堂教学；

（3）数学文化和数学史的融入需要课内、课外相结合。教学课时的有限性导致我们在课堂教学中能够学习的内容是有限的，数学文化和数学史的融入必然要占用一定的教学时间，我们想这也是导致HPM研究高评价、低应用的一个重要因素[3]。因此，在教学中我们不仅要在数学材料的深度加工和应用方法的恰当选取上下功夫，提高课堂教学效率，还应该课内、课外相结合，引导学生通过网络、图书等各种平台和途径自主收集、整理相关数学史材料，学习相关数学文化和数学史，以达到对数学文化和数学史的深入学习和理解。

结  语

数学文化和数学史作为数学学科的历史积淀，是数学学科的精髓所在，是提高学生数学学科核心素养的重要载体。HPM的研究取得了很多令人瞩目的成果，很多一线教师也通过教学实践研究开发出了很多HPM视角下的优秀课堂教学案例。但笔者认为，HPM的研究是常做常新的工作，面对不同的教学内容、不同的数学史材料和不同的学情，数学史材料的选取，融入课堂的方式应有所差异。对于相同的教学内容、同样的数学史材料和相似的学情，教师也会有不同的教学设计思路和教学方法。笔者认为这就是教学的魅力所在，也只有这样我们的教学才能真正面向全体学生，实现“人人都能获得良好的数学教育，不同的人在数学上得到不同的发展”的数学教学目标[4]。

[参考文献]

中华人民共和国教育部.普通高中数学课程标准（2017年版）[M].北京：人民教育出版社，2020.

张建跃，李增滬主编.普通高中教科书数学必修第二册[M].北京：人民教育出版社，2019.

教育部考试中心.中国高考评价体系[M].北京：人民教育出版社，2019.

汪晓勤，王甲.全等三角形的应用：从历史到课堂[J].中学数学参考（初中版），2008（10）：55-57.

基金项目：本文系景东彝族自治县科学规划2021年度课题“HPM视角下的高中数学教学实践研究”（课题批准号：21X03）的研究成果之一。

作者简介：李德明（1990.3-），男，彝族，云南景东人，任教于云南省普洱市景东彝族自治县银生中学，一级教师，研究生学历。