GM(1,N)模型的病态性研究及其在生态创新中的应用
熊萍萍, 李田田, 檀成伟, 武彧睿
(1.南京信息工程大学 风险治理与应急决策研究院,江苏 南京 210044; 2.南京信息工程大学 气象灾害预报预警与评估协同创新中心,江苏 南京 210044; 3.南京信息工程大学 管理工程学院,江苏 南京 210044; 4.南京信息工程大学 数学与统计学院,江苏 南京 210044)
0 引言
习近平总书记在二十大报告中明确指出,“创新是第一动力,创新驱动发展战略,坚持创新在我国现代化建设全局中的核心地位”,同时要推动绿色发展,促进人与自然和谐共生,表明了国家对绿色发展、生态文明建设的坚定信念。工业企业是实施技术创新向生态创新转化的最主要行动者。由于生态创新多投入和短期效果不明显,严重阻碍了生态创新的发展。因此,生态创新相关指标的数据量有限,企业生态创新系统结构复杂,具有一定的不确定性、贫信息等特征。
邓聚龙教授针对小样本数据特征创立了灰色系统理论。其中离散GM(1,1)模型建模时的病态性会导致模型的不稳定性,便运用向量的数乘和旋转变换将矩阵转化为良态矩阵[1]。针对病态性问题的研究还有利用数乘变换解决了引入累积法对模型参数估计时产生的病态问题[2],以矩阵谱条件数研究灰色Verhulst扩展模型的病态性[3],基于矩阵求逆的条件数探讨GM(1,1)幂模型的病态性[4]。
GM(1,N)模型包含一个系统特征变量和N-1个影响因素变量,但该模型在建模机理、参数求解和模型结构方面存在缺陷,故学者对GM(1,N)进行了优化。对具有卷积积分的GM(1,N)模型赋予新的权重,提出新信息优先积累方法改变模型结构[5];考虑系统行为变量和相关变量可能存在非线性关系,引入非线性参数,如基于核函数提出的非线性KGM(1,N)模型[6],基于伯努利方程提出的灰色伯努利NGBM(1,1,k,c)模型[7]等,这些模型的基本思想都是引入非线性公式,将其转化为线性形式,再建立多元灰色模型。参数求解方面,在GM(1,N)模型的驱动项上引用幂指数,建立了GM(1,N)幂模型,采用智能优化算法求解幂指数和对模型进行参数估计[8]。此后也将GM(1,N)模型从实数序列拓展到灰数序列用于预测[9]。
GM(1,N)模型在进行建模时,需要满足各影响因素之间相互独立才能确保模型的建模效果合理。然而在实际应用中,影响因素之间多存在一定的相关性,导致在利用普通最小二乘法对模型进行求解时,协方差矩阵因接近奇异而使得模型的解出现过拟合的现象。这种情况下,我们将它认为模型出现了病态性。然而在现有的研究中,针对GM(1,N)模型病态性问题的改进仍存在不足。本文由此提出基于L2范数的最小二乘法,对模型的参数估计进行优化,以此解决模型求解时面临的病态性问题。为了弥补参数缺陷,由差分方程直接进行参数估计和求解时间响应式,从而确保参数应用的同源性。对GM(1,N)模型的建模进行优化以后,进行案例分析,将该模型应用到工业企业专利数的预测中,通过实例分析,进一步验证本文优化模型的合理性和有效性。
1 GM(1,N)模型
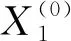
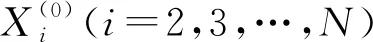
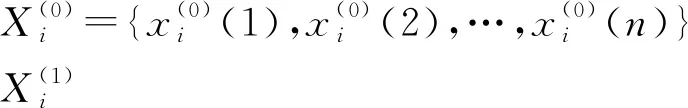
(1)
为GM(1,N)模型。
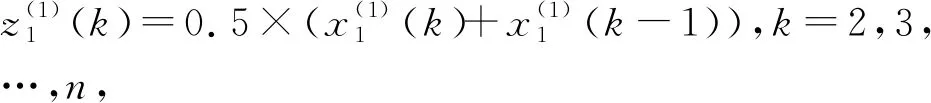
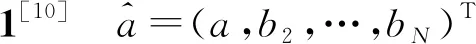
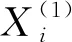
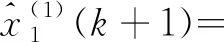
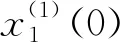
2 带L2正则项的GM(1,N)模型的建模机理
由于灰色预测模型GM(1,N)针对小样本数据进行拟合,在面临变量个数多于样本个数问题或者影响因素间存在强关联性时,使用最小二乘法进行参数求解,可能会出现矩阵BTB奇异化,导致参数列解的不稳定。所以本文提出引入L2正则项的最小二乘法进行参数估计,其算法原理是在残差平方和函数上增加L2正则项,通过最小化所有系数达到目的,以此解决模型求解的病态性问题。
2.1 基于优化算法的GM(1,N)模型的参数估计
2.1.1 带L2正则项的最小二乘法
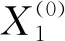
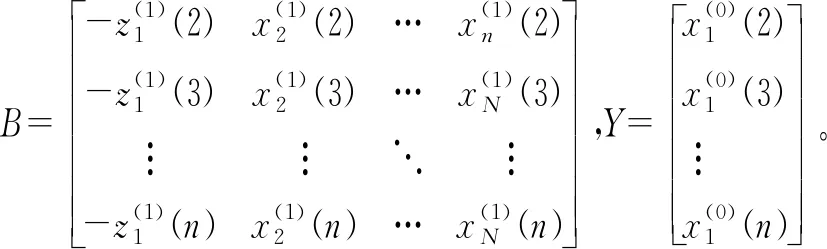
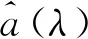
2.1.2 带L2正则项的最小二乘法的性质
探讨引入L2正则项的最小二乘法对GM(1,N)模型进行参数估计的性质。
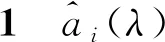
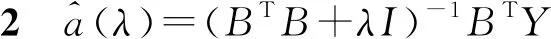
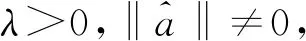
从性质1至性质3出发可以得到,模型的参数估计虽然失去了普通最小二乘法的无偏性,但合适的正则项系数能够有效的解决模型参数估计时均方误差较大的问题,使得模型的估计更加的稳定、合理。同时也验证了基于L2范数约束的最小二乘法,能够解决模型估计时存在的病态性问题。
2.2 带L2正则项的GM(1,N)模型的解
本文将直接通过构造模型的方程来得到参数估计和时间响应式,这样就可以确保参数估计与参数应用的同源性。
定理3GM(1,N)模型如式(1)所述,则
(i)当k=2,3,…,n时,模型的时间响应式为
(ii)当k=2,3,…,n时,模型的累减还原式为
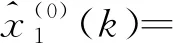
(4)
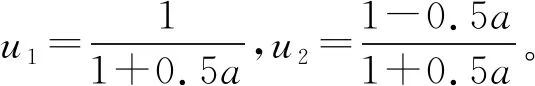
2.3 参数λ的确定
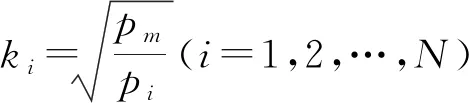
2.4 模型的精度检验
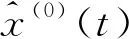
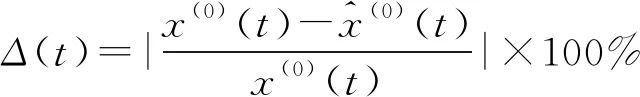
(5)
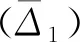
(6)
(7)
模型拟合和预测的精度高低是衡量所构建模型好坏的重要标准,规定当模型平均相对拟合误差和平均相对预测误差均小于10%,则称构建的模型通过误差检验。
3 实例分析
3.1 江苏省工业企业专利数预测
3.1.1 变量的选取
本文采用工业企业专利数作为生态创新的衡量指标[11]。由于生态创新的发展受到经济发展水平[12]、政策扶持力度[13]等多方面的影响,因此考虑了多个因素对其产生的影响,以期能更好地预测工业企业专利数。
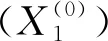
3.1.2 模型的建立
步骤1根据选定的数据,计算系统行为变量与影响因素变量之间的灰色绝对关联度,结果如下:
ε12=0.68,ε13=0.69,ε14=0.62,ε15=0.67,ε16=0.64
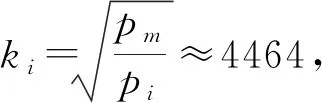
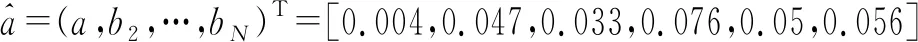
步骤3构建GM(1,6)模型。根据定理3,得到GM(1,6)模型为
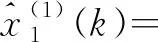
步骤4计算优化模型与对比模型的模拟值和平均相对误差,结果如表1。
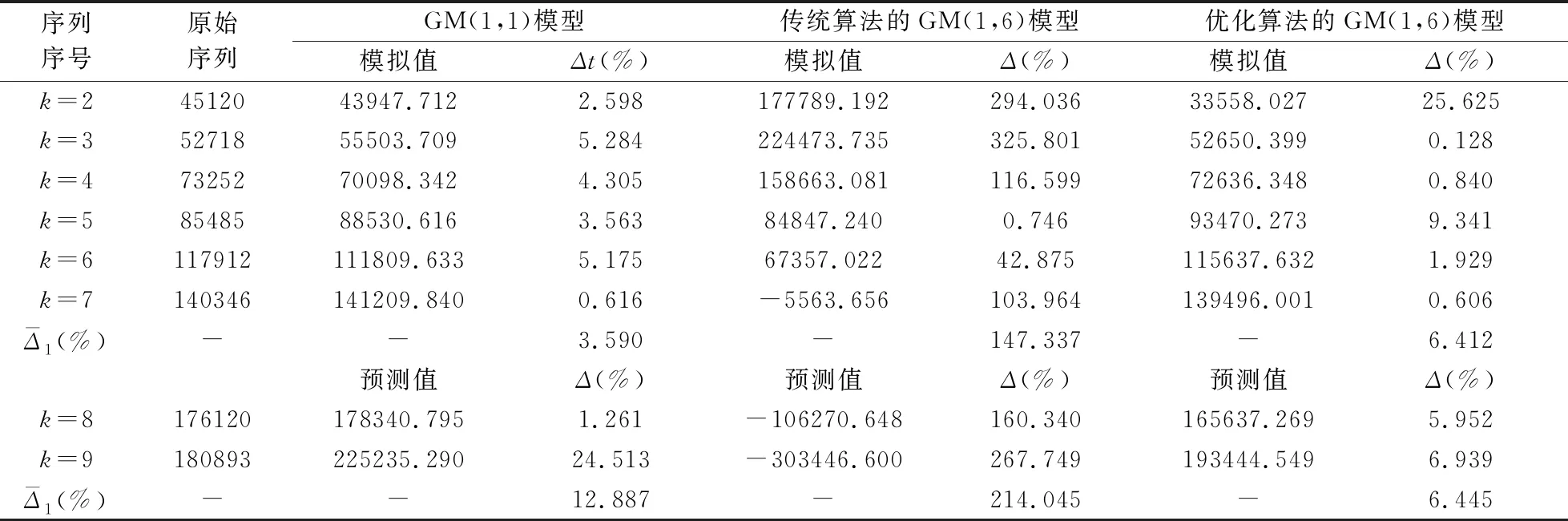
表1 灰色模型比较
由表1可以看出优化的GM(1,6)模型的平均相对模拟误差是6.412%,平均相对预测误差是6.445%,且均小于10%,说明模型的模拟精度和预测精度都高,模型建立合理。
3.1.3 模型比较
(1)优化灰色预测模型与其他灰色预测模型比较
将不同算法的灰色模型进行比较,三种方法的预测结果,如图1所示。
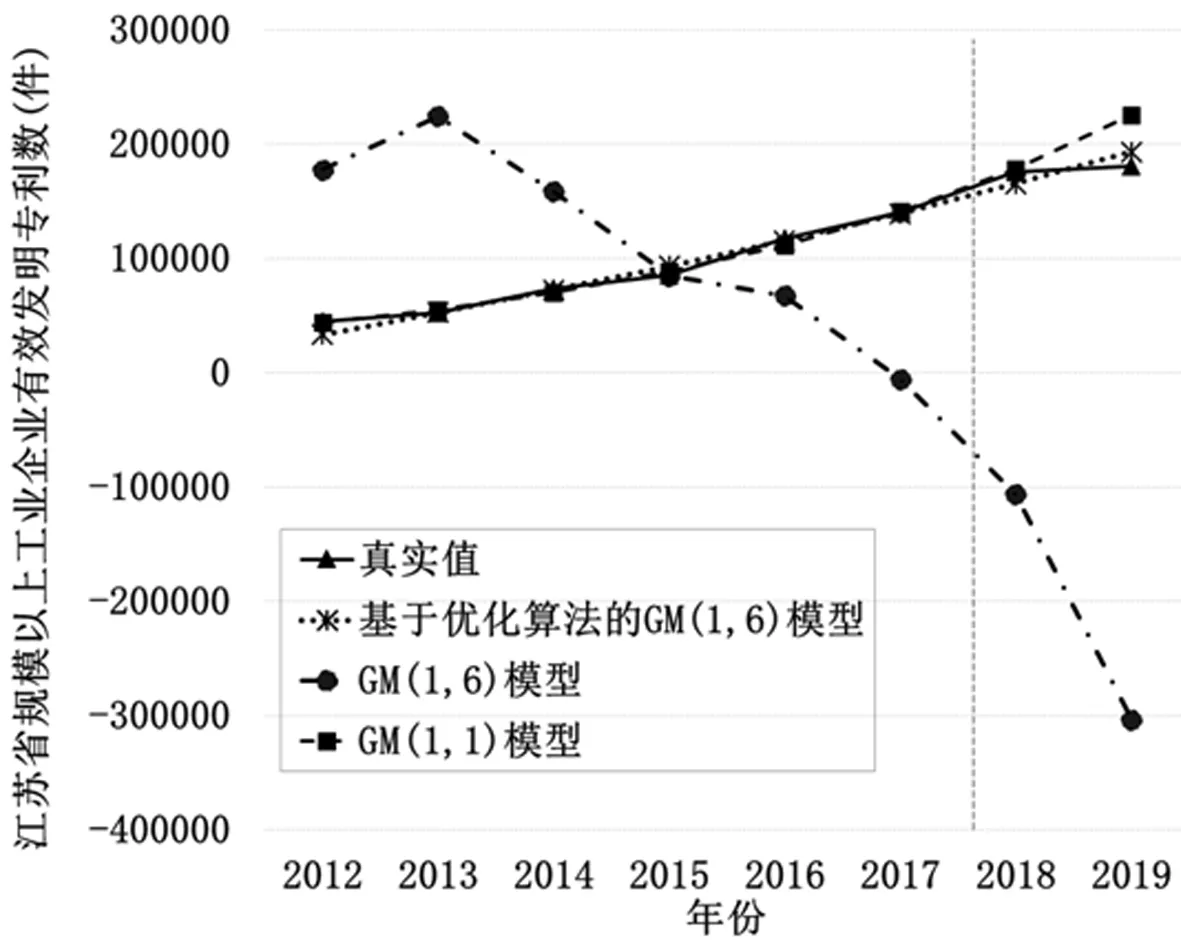
图1 预测模型比较
通过图1看出传统算法的GM(1,6)模型预测结果与真实值相差过大。 GM(1,1)模型的平均相对模拟误差和平均相对预测误差分别为3.59%和12.887%。三种预测方法中,虽然GM(1,1)模型的模拟效果比改进算法的模型好,但是预测误差大于10%,其次GM(1,1)模型只根据工业企业有效发明专利数这个指标进行模拟预测,没有充分考虑其他因素对其产生的影响,而优化算法的GM(1,6)模型无论是模拟误差还是预测误差均低于10%,且将各方面的影响因素考虑进其中。
(2)优化模型与统计模型比较
将江苏省规模以上工业企业有效发明专利数(件)作为因变量,规模以上工业企业开发新产品经费(万元)、地方财政科学技术支出(亿元)、城市污水日处理能力(万立方米)、地区生产总值(亿元)和规模以上工业企业流动资产合计(亿元)作为自变量,建立多元回归模型。由R软件得出的回归结果知:这五个自变量与规模以上工业企业有效发明专利数之间的相关系数都大于0.9,由此认为它们之间存在高度相关,说明自变量对因变量存在影响,故建立多元线性回归模型。
选取我院2016年1月~2018年1月收治的100例冠心病患者,所有患者年龄均超过60周岁,分介入组和药物组,各50例。药物组:男24例、女26例,年龄62~80岁,平均72.8±5.4岁;介入组:男26例、女24例,年龄60~78岁,平均70.8±6.4岁。两组患者的一般资料,无统计学差异性。
在显著性水平α=0.05下,得到F值为77.75,大于临界值Fα(5,4)=6.26,通过显著性检验,说明因变量与自变量之间存在线性关系。接着对各回归系数分别进行t检验,以判断每个自变量对因变量的影响是否显著。所有的自变量均未通过检验,说明多元回归建立是不合理的。计算得自变量的方差扩大因子VIF大于10,说明多元回归模型存在严重的多重共线性,故使用岭回归建模。
岭回归结果显示,当k值较小时,参数列的值很不稳定,当k值逐渐增大时,各参数趋于零,此时选择k值为0.04,各参数值基本上都能相对稳定。并将模拟结果和预测结果与灰色预测模型比较,比较结果如表2所示。
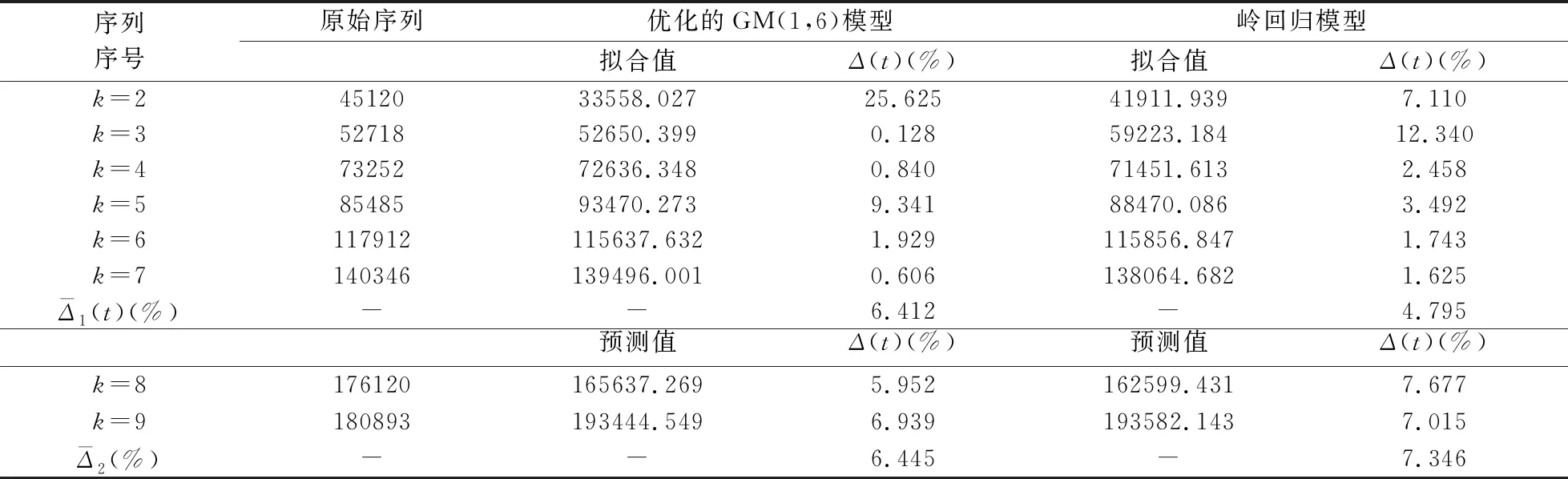
表2 灰色预测模型与统计模型比较
由表2得出岭回归模型的平均相对模拟误差为4.795%,平均相对预测误差为7.346%。它的模拟效果优于基于优化算法的GM(1,6)模型,但是预测效果不及基于优化算法的GM(1,6)模型。而且生态创新具有样本量少,影响因素结构复杂导致不确定性等灰色特征,故使用灰色预测模型进行模拟预测更具有实际意义。
由此可以看出灰色模型预测效果更好。统计模型是基于概率统计基础上进行回归预测的,一般来说,样本数量越大,得到的预测效果越好,而针对于小样本数据,统计模型获得的有用信息少,所以导致预测效果不好,此时更适合选择灰色模型进行预测。根据基于优化算法的GM(1,6)模型的结果来看,江苏省规模以上工业企业有效发明专利数呈指数递增趋势,其中地方财政科学技术支出和规模以上工业企业流动资产合计对生态创新的发展起到了更重要的影响作用。
3.2 华北地区工业企业专利数预测
3.2.1 变量的选取
本实例选取来自国家统计局2011~2019年的华北五省工业企业有效发明专利数,采用华北地区规模以上工业企业有效发明专利数(件)作为系统行为变量。以规模以上工业企业单位数(个)、供水综合生产能力(万立方米/日)、城市污水日处理能力(万立方米)、工业污染治理完成投资(万元)和规模以上工业企业R&D人员全时当量(人年)为相关影响因素指标,将2011~2017年的数据为训练集,2018~2019年数据为测试集。
3.2.2 模型的结果比较
基于优化算法的GM(1,6)模型的平均相对模拟误差是7.598%,平均相对预测误差是1.778%。说明模型的模拟和预测精度都高,模型建立合理。将基于优化算法的GM(1,6)模型与传统算法的GM(1,6)模型、GM(1,1)模型和岭回归模型进行比较,为了更加直观描述各个模型的建模效果,对比结果如图2所示。
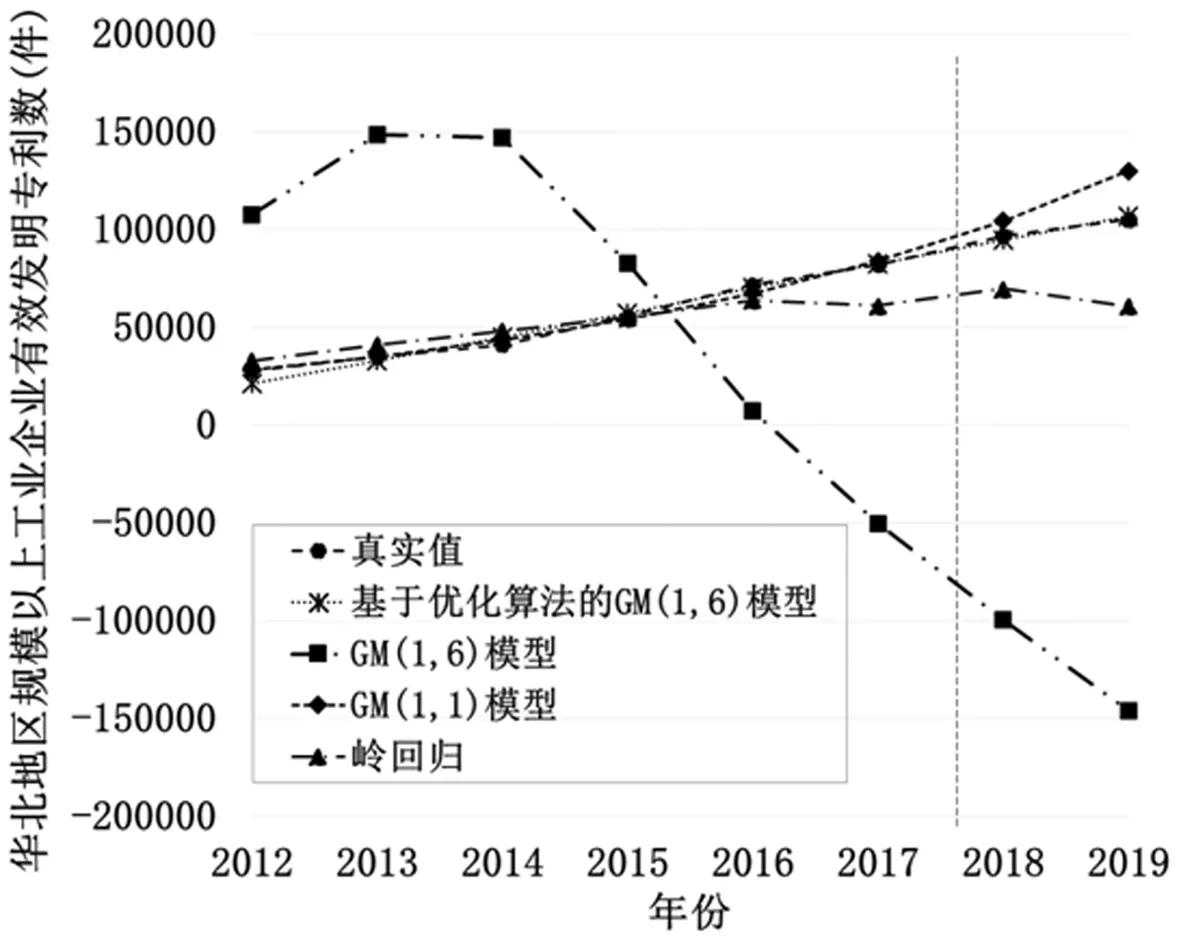
图2 模型结果比较
从图2可以得出GM(1,6)传统算法的解不稳定,其模拟和预测效果都偏离真实值,与原序列的发展趋势相违背,从而验证了若模型求解存在病态性,使用传统算法求解的结果并不具备参考价值。预测模型GM(1,1)的平均相对模拟误差为2.906%,平均相对预测误差为15.770%,虽然模拟效果较好,但是预测误差大于10%,没有通过模型的误差检验。而基于优化算法的GM(1,6)模型,无论从模拟效果还是预测效果,都通过了误差检验,并且得出的解具有稳定性,解决了模型求解的病态性问题。统计模型岭回归的平均相对模拟误差为15.025%,平均相对预测误差为35.059%,模拟和预测效果都不如本文提出的灰色预测模型效果好,这也证实了对于具有灰色特征的数据,使用灰色模型进行预测,效果更好。
4 结论
传统算法的GM(1,N)模型具有参数应用缺陷和病态性问题,本文通过引入L2正则项的最小二乘法进行参数估计,有效的解决了病态性问题。由模型的差分方程直接得到时间响应式和参数求解,从而保证了参数来源的统一性,避免了参数缺陷。将优化算法的模型运用到生态创新数据中,并将结果与其它灰色预测模型和统计模型进行比较,结果表明,优化算法后的模型模拟和预测误差通过精度检验,且预测结果具有参考价值。在小样本数据下,灰色模型的预测性能优于回归模型,从而验证了灰色模型适用于小样本、具有灰色特点的数据,能够更好地进行预测。这不仅丰富了灰色预测模型的理论体系,也为生态创新相关指标预测提供了新的方法。
本文仍存在一定的不足之处。在对正则项系数进行确定时,本文偏好性地利用了粒子群算法在拟合误差最小的条件下确定了相对最优的正则项系数值,使得模型的参数估计更加合理,以此消除了模型的病态性问题。但在该算法下确定正则项系数未必对所有的实际应用都可行,可能出现建模效果不佳。因此,读者还可以从均方误差最小准则或者绝对误差最小准则出发,选择其它优化算法找到模型的相对最优正则项系数值,以解决模型的病态性问题。

