基于RBF函数的茶饮数据分析与预测
李锦朋,黄贻望,2*
(1. 铜仁学院大数据学院,铜仁 554300;2. 贵州省公共大数据重点实验室(贵州大学),贵阳 550025)
0 引言
随着数据技术的发展,企业转型数字化成为必然的趋势,如何去收集、挖掘、分析大数据加快企业的转型数字化发展是企业信息化的一个重要功能[1]。某餐饮品牌是贵州本土品牌,成立于2013 年,结合本土各种好茶叶,酝酿出各种好口碑的奶茶,随着店面不断增加,销售数据也日益增加,现有简单的数据统计图应用无法支撑一个企业快速发展,根据某茶饮销售过程中产生的异构数据,利用支持向量机(sup‑port vector machine,SVM)小样本算法构建基于不同核函数的销售额预测分析模型,通过对不同核函数下SVM 销售额预测模型的对比分析,得到参数调优后的SVM 销售额预测值与实际销售额的值进行比较[2]。实验仿真表明,参数优化后的SVM 可减少数据中噪声数据的影响,提高了销售预测模型的效率[3]。
实现某茶饮销售数据动态适时分析与预测具有重要的意义,能对企业未来的趋势进行风险预测,并能及时制定解决方案。通过公司的海量数据分析出产品与产品之间的关联模式、天气对企业销量的影响等诸多因素。通过图表观察数据的整体情况可探究历史企业整体运营情况、业务组成,以便了解企业每个业务的动态发展变化,所有店铺及单个店铺销售情况、消费者(口味、喜好)以及同行的经营状况等,从数据到实际生活等多个维度来定制数字化服务,从而实现企业的快速发展[4]。
主要贡献:①获取某茶饮历史销售数据集及时间段内地区气温温度;②在企业运营系统获取到的数据集进行预处理;③构建基于支持向量机的销售额预测模型;④将非线性SVM模型的预测销售额与真实销售额进行对比分析,有比较好的吻合度,说明模型具有较好的泛化性能。
1 某茶饮数据的支持向量机模型构建
1.1 模型定义
某茶饮销售额受到多种因素,如天气温度、消费者购买力、节假日、门店地域不同等影响,不同的门店位置、不同的人群购买力产生的销售额不同,选择消费者购买力、天气温度、节假日等特征值建立销售额关系的预测模型,利用支持向量机(SVM)方法可以实现销售额是否达到预期目标的预测,有效提升产品的销售布局和管理决策。
解决办法是根据已有的销售数据在模型中的多样性和学习能力之间寻求最好解决方案[11],SVM 解决海量数据中非线性问题的核心思想是原始的非线性可分数据X 可找到一个非线性映射Φ,该映射Φ 将非线性可分的原始特征空间投影到线性可分的高维特征空间F,从而在高维特征空间中实现样本的线性分类或回归[5]。由于SVM 可以实现对特定训练样本的学习并分类识别,将SVM预测模型应用于销售额预测领域,通过对数据集的预处理,使用SVM 可减少噪声数据对预测的影响并在分析过程中提高了SVM模型的准确性[6]。
设有M个数据样本的数据集,其中xi∈Rd是d维向量,表示每个数据样本的输入特征值向量,yi∈{+ 1, - 1} 是每个数据样本的标签,表示样本属于的类别,则使用模型对该数据集中的样本进行预测的约束条件为
将 公 式(1)合 并 为yi(ωTxi+b) ≥+1,i=1,2,…,m,其中ω=(ω1,ω2,…,ωd)为特征向量的权重向量,决定分类超平面的法向量;b为截距,表示超平面与原点之间的距离,记为(ω,b)。
数据集中任意样本x到分类超平面(ω,b)的距离公式写为
从而优化目标函数为
通过对(ω,b)进行缩放使得|ωTx+b|= 1,则将式(3)转化为式(4):
为降低基于SVM 销售额预测模型的泛化误差[7],引入松驰变量ξi,将优化目标转化为
1.2 优化目标函数求解
通过引入拉氏(Lagrange)系数,构造拉氏函数,将式(5)化为无限制的优化问题,拉格朗日乘子αi≥0,i= 1,2,…,N,拉氏函数如下:
当满足对应的KKT条件时,
无约束优化问题式(6)转化为相应的强对偶问题:
通过求解公式(8)得到原问题的优化解,见式(9)。
2 数据处理
2.1 数据集
数据集是采用贵州某餐饮品牌实时销售数据,某店 面2015 年1 月1 日 至2021 年7 月31 日每一天的销售额数据,数据集包含2826 行10 列的时间-销售金额数据。如表1所示。
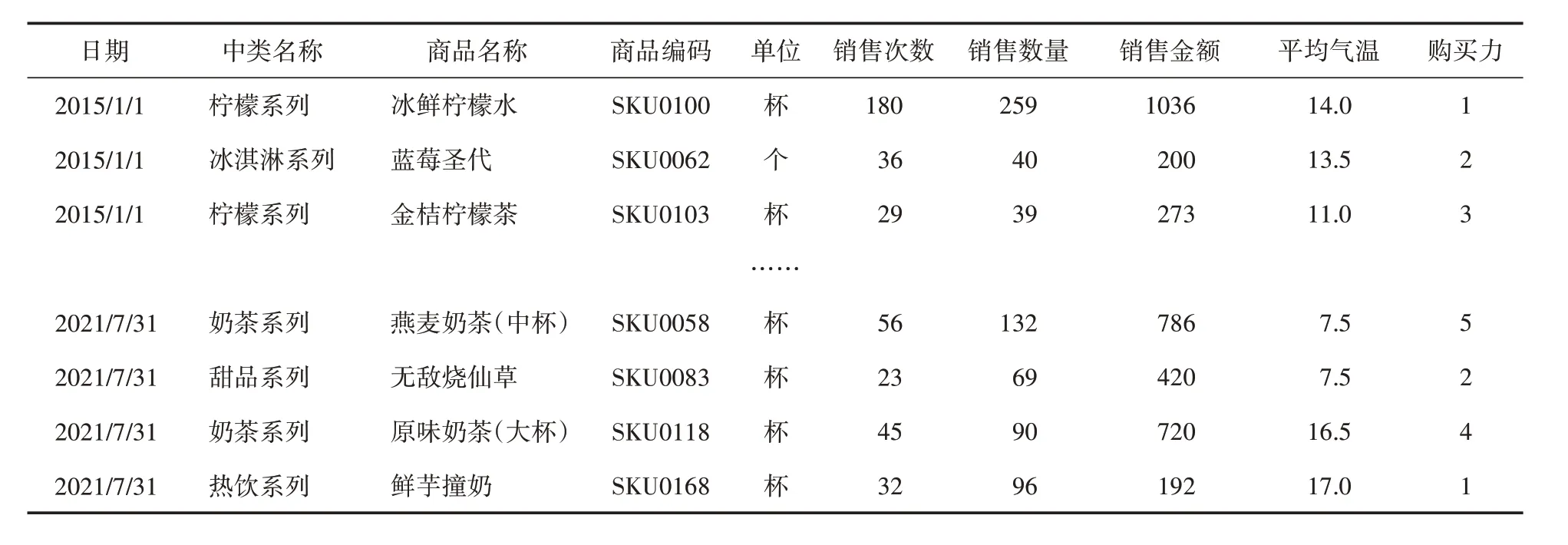
表1 茶饮销售数据源
2.2 特征选择
为防止多维属性的强关联对茶饮样本数据质量产生噪声,从而影响模型的可靠性,从一级品类、二级品类、商品名称、商品编码、单位、销售次数、销售数量、销售金额、退货数量、退货金额等10 个特征中选择对预测销售额影响较大的特征,即样本空间属性的降维处理,也就是特征选择,从而降低预测过程的复杂性,同时由于是针对餐饮店销售额的预测,将加入影响销售的外界因素天气温度、购买力作为特征值,共计12 个特征,通过降维到4 个属性用于模型的训练。图1为各属性贡献值。
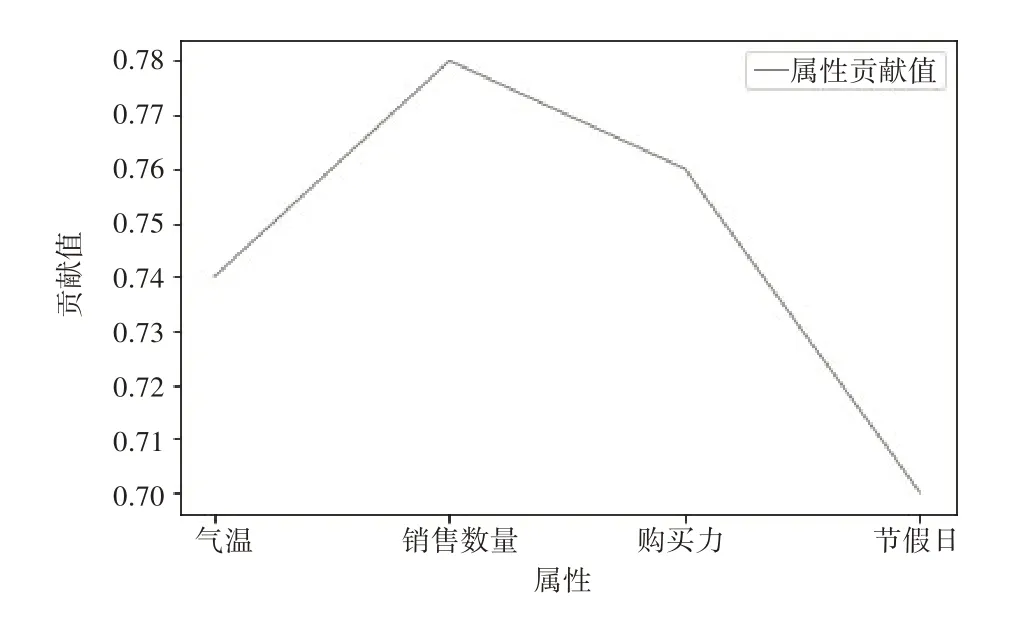
图1 各属性贡献值
2.3 销售额的参数
影响销售额的参数有气温、购买力、节假日、销售数量,其中气温和购买力是长期影响销售额的因素。
气温数据从国家气象网上采集,政府部门发布的统计数据可提供人群购买力的参考指标,比如人均收入、消费支出等。图2和图3是影响销售额的气温和购买力,销售数量与销售额呈正比,随着节假日到来,销售额也会随之增长,影响销售额的还有门店位置。
图2 气温
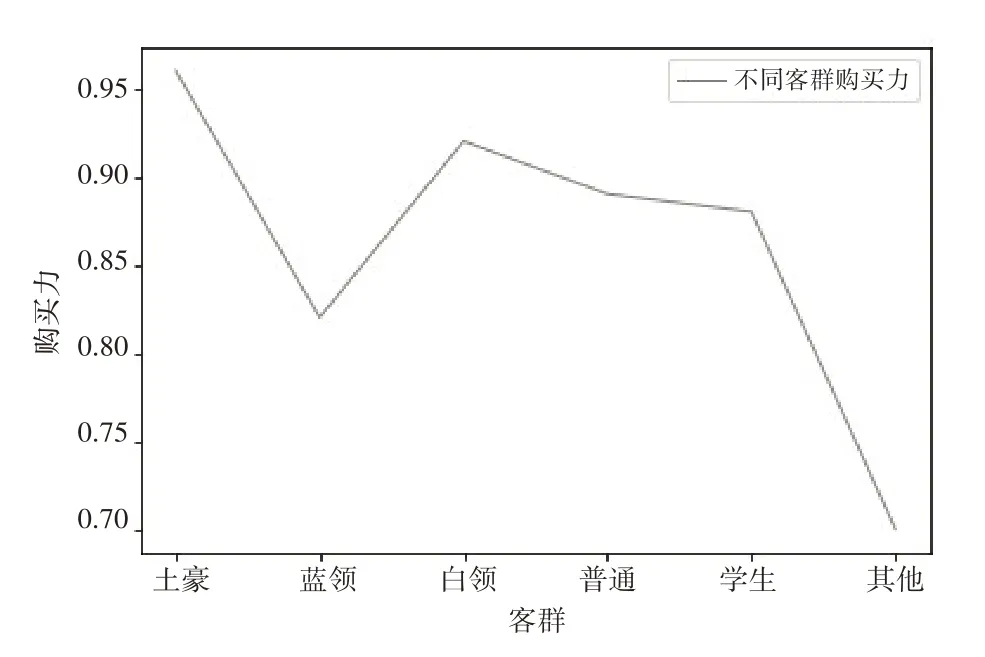
图3 客户群购买力
2.4 归一化
为解决因特征变化而导致的预测偏差,需要对数据集进行归一化处理,这里采用min⁃max标准化[8],如公式(10)所示。
其中:xi为第i个样本数据属性值,xmin和xmax是属性的最小值和最大值。
归一化后的销售额数据可以提升模型精度和准确性,图4(b)是将实际销售额数据归一化后的结果。
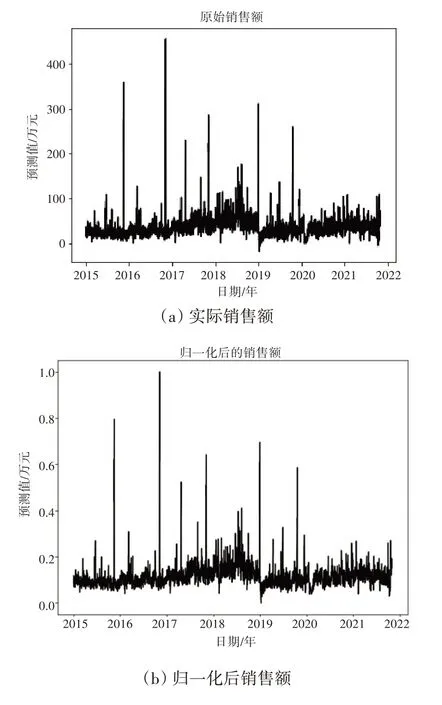
图4 标准化后的数据对比
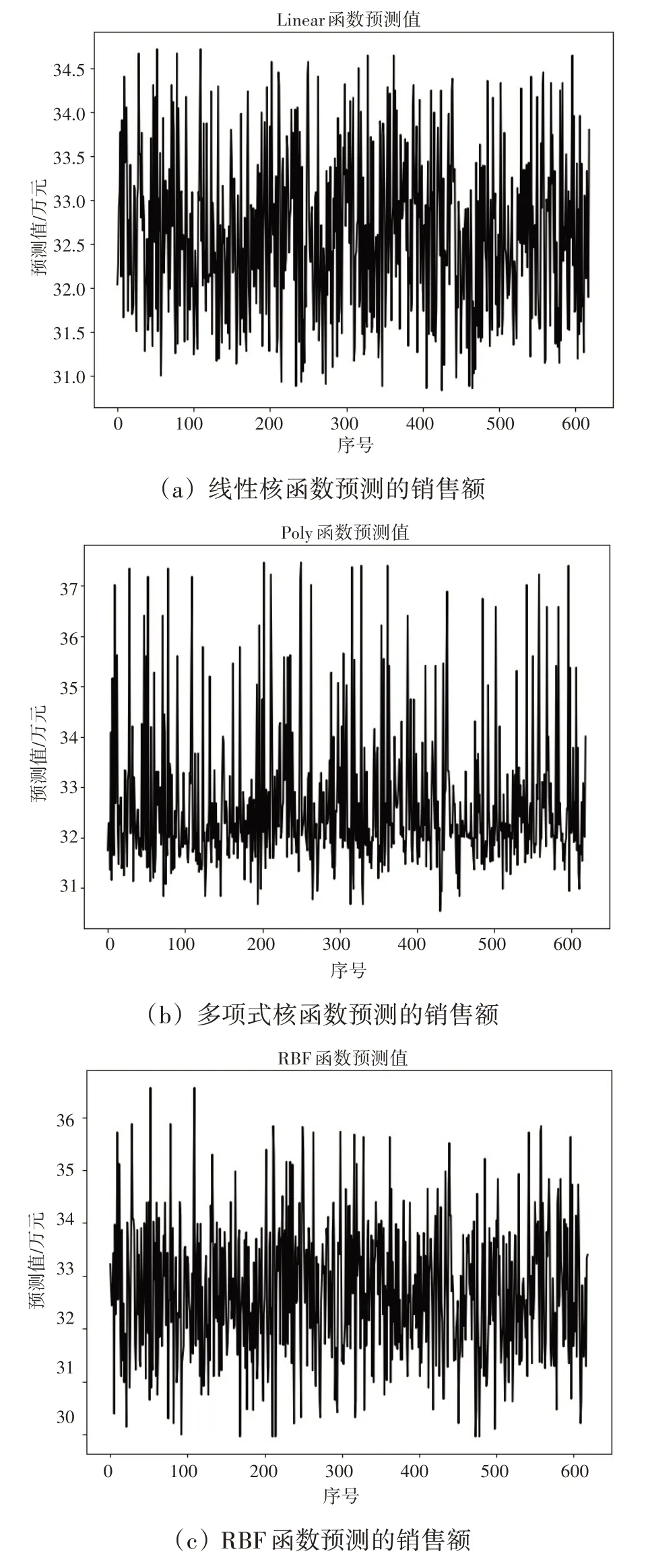
图5 三种核函数销售额预测对比
3 实验和分析
3.1 基于不同核函数的SVM销售额预测模型
将2826 条数据分为训练集和预测集,其中1978 条数据作为训练集,848 条数据作为测试集[9]。模型训练是基于线性核、多项式核和RBF核三种不同的核函数进行的,通过三种不同核函数构造SVM销售额数据的预测模型,其中RBF核为高斯核,对应的函数为高斯核函数(见表2)。

表2 核函数的表达式
选取均方误差(MSE)和平均绝对百分比误差(MAPE)两个评价指标分别从预测误差和预测精准度两个方面对不同核函数下的SVM 销售额预测结果进行对比[10],结果如表3所示。
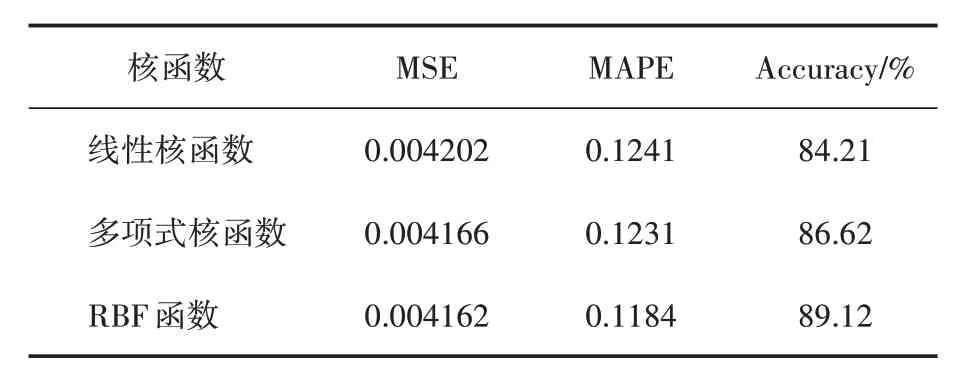
表3 三种核函数销售额预测对比
据统计分析可知,均方误差(MSE)越小,表示预测值与真实值误差越小,即分类模型性能越好,也就是说模型的预测结果越接近真实值[11],从表3可知基于高斯核函数(RBF)的支持向量机模型的预测销售额效果较其余两个函数的效果更佳[12]。
3.2 参数调优
为降低预测销售额模型的预测误差,提高模型的泛化性能,现对RBF 函数下的SVM 销售额预测模型的参数进行优化。随机选取3组参数对(σ,δ)进行对比实验,其中σ为惩罚参数,δ为多项式函数的系数,对比结果如图6所示[13]。
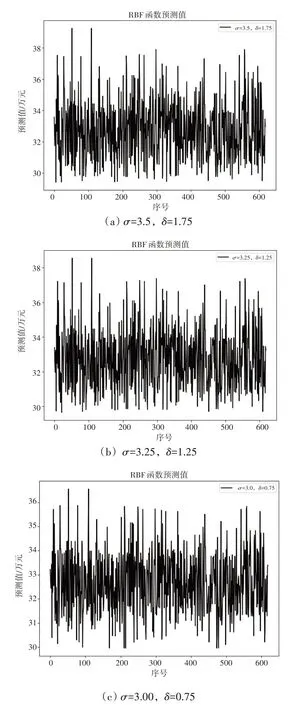
图6 基于不同参数的SVM的预测结果对比
对比表3 和表4 销售预测模型的MSE、MAPE 和Accuracy,得 到σ=3.00,δ=0.75 时,RBF 核函数MSE=0.004115,MAPE=0.0964,Accu‑racy=92.14%,表明SVM预测效果较好。
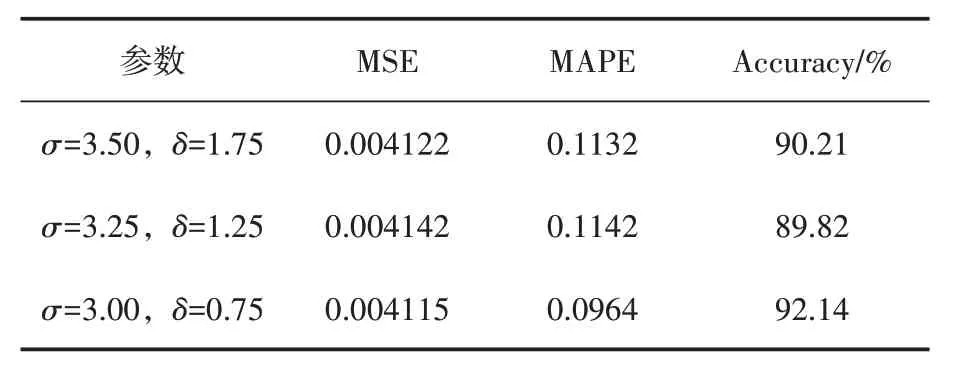
表4 基于不同核函数销售额预测对比
由表4 可知,对参数调优前后MSE、MAPE的值进行对比,发现参数调优后模型预测效果更佳[14]。
4 结语
将销售数据作为训练集,训练不同核函数下的SVM 销售预测模型,并对RBF 函数SVM 销售预测模型进行参数优化,通过对SVM 模型预测结果误差和准确率进行仿真分析,验证了优化后模型的有效性,有助于企业精准掌握客户喜好,针对不同的客户群采用不同的方案进行精准营销。

