The dynamic relaxation form finding method aided with advanced recurrent neural network
Liming Zhao | Zhongbo Sun| Keping Liu | Jiliang Zhang
1Department of Mechanical and Electrical Engineering, Changchun University of Technology,Changchun,China
2Department of Control Engineering, Changchun University of Technology,Changchun,China
3Department of Electronic and Electrical Engineering, The University of Sheffield,Sheffield,England
Abstract How to establish a self-equilibrium configuration is vital for further kinematics and dynamics analyses of tensegrity mechanism.In this study,for investigating tensegrity formfinding problems,a concise and efficient dynamic relaxation-noise tolerant zeroing neural network (DR-NTZNN) form-finding algorithm is established through analysing the physical properties of tensegrity structures.In addition, the non-linear constrained optimisation problem which transformed from the form-finding problem is solved by a sequential quadratic programming algorithm.Moreover, the noise may produce in the form-finding process that includes the round-off errors which are brought by the approximate matrix and restart point calculating course, disturbance caused by external force and manufacturing error when constructing a tensegrity structure.Hence, for the purpose of suppressing the noise,a noise tolerant zeroing neural network is presented to solve the search direction,which can endow the anti-noise capability to the form-finding model and enhance the calculation capability.Besides, the dynamic relaxation method is contributed to seek the nodal coordinates rapidly when the search direction is acquired.The numerical results show the form-finding model has a huge capability for high-dimensional free form cable-strut mechanisms with complicated topology.Eventually,comparing with other existing form-finding methods, the contrast simulations reveal the excellent antinoise performance and calculation capacity of DR-NTZNN form-finding algorithm.
K E Y W O R D S dynamic relaxation, form-finding, noise-tolerant zeroing neural network, sequential quadratic programming,Tensegrity
1 | INTRODUCTION
The tensegrity structures have been widely used in the fields of large-scale dome architecture,sculpture,and biomimetic robot[1–3].The tensegrity form-finding course is a crucial step for further analysis of tensegrity structure.Thereby,how to investigate an efficient form-finding method is a long-standing challenge.In the past decades, many researchers pay their attentions to the tensegrity form-finding approaches.Many efficient form-finding methods have been developed, in these approaches, the dynamic relaxation form-finding algorithm realised tensegrity form-finding course by using a pseudo dynamic process[4,5].The dynamic relaxation method regarded the form-finding procedure as a process of calculating the nodal coordinates masses and kinetic energy of nodal coordinates.The velocity and external force have been evaluated during each iteration step [4].According to the numerical examples, the form-finding calculating process can be improved the convergence speed and optimisation precision through the dynamic relaxation (DR) method.Besides, the algorithms which transformed the form-finding problems into non-linear and linear optimisation problems have become a significant constituent part of form-finding methods [6–12].But most of the formfinding approaches have not involved the noise-suppressing during the form-finding process.In ref.[13], the tensegrity form-finding problem has been considered as a constrained optimisation problem.This paper has proposed a modified three-term method combined with the damping dynamic relaxation method.Furthermore, in ref.[14], a modified noise tolerant zeroing neural network(NTZNN)form-finding model has been applied to establish a self-equilibrium structure through solving the non-linear optimisation form-finding problem which is under the noise polluted.However,although the presented method can suppress the noise items during the form-finding procedure, whereas, when facing large-scale structure, the algorithm cannot manage the form finding problems efficiently due to the structural complexity.In summary,how to establish a universal and simple model with noise suppression functionality is important for further analyses of tensegrity form-finding approaches.
In this paper,the form-finding problem is transformed intoa non-linear constrained optimisation (NCO) problem.As for a non-linear optimisation problem with constraint conditions, it can be solved by the sequential quadratic programming (SQP)method [15].In general, in order to reduce the calculation complexity,the SQP algorithm utilises quasi-Newton method to calculate approximate matrix to instead of Hessian matrix.The round-off error is occurred between the Hessian matrix and the approximate matrixBk.Hence, as a kind of recurrent neural network (RNN), which is a powerful intelligence algorithm to solve the non-linear optimisation problems,the NTZNN algorithm has the superiority of parallel computing and high precision [16–27].In addition, the NTZNN algorithm has a wide range of applications in dealing with discrete-time non-linear optimisation problems [28], continuous-time non-linear optimisation problems[29],and controller design[30].Furthermore,compare with the RNN models, the NTZNN model has the advantage of anti-noise performance[18,31,32].In the actual form-finding process, the noise includes the round-off error caused by approximate matrixBk,calculating error and external force interferences to the tensegrity mechanism.Therefore,the NTZNN model gets the upper hand for forming a tensegrity form-finding approach.
In order to establish a self-equilibrium and stable tensegrity structure, the objective function is constructed through analysing the target length and presented length of the strut elements.And the constraint conditions are designed based on the physical properties of the force density vector.Hence, a simple and effective form finding model is constructed through above analyses.In addition,the form-finding problem is transformed into a quadratic programming problem which the nodal coordinates are the variables.Hence, the NTZNN model is utilised to deal with the search direction and the nodal coordinates are obtained by dynamic relaxation method.In conclusion, a dynamic relaxation-noise tolerant zeroing neural network (DR-NTZNN) form-finding algorithm with simple construction and high-efficiency calculated performance is established through above strategies.Besides, the model has excellent anti-noise performance while the other form-finding algorithms do not have.Before the end of this section, the main contributions of the paper are organised as follows:
1) The DR-NTZNN form-finding algorithm transforms the
form-finding problem into NCO problem.Due to the NTZNN model is involved in the form-finding model designing course, hence, the DR-NTZNN form-finding algorithm has excellent anti-noise performance.In this sense, it is quite unique with the existing DR form-finding methods.
2) The stability,consistency,and convergence performances of the NTZNN model are investigated through theory analyses.By means of the theoretical evaluations, it proves the DRNTZNN method withO(ι2) pattern round-off error can satisfy the tensegrity structure form-finding requirements.
3) The computational efficiency and anti-noise properties of the DR-NTZNN form-finding algorithm under noise interference are verified by two-dimensional and threedimensional tensegrity structure simulations.In addition,the simulation results of high dimensional tensegrity structure show the DR-NTZNN algorithm is effective in solving the form-finding problems of complicated topological structure tensegrity mechanism.
2 | FORM‐FINDING MODEL FORMULATION
2.1 | Optimisation model
During the form-finding process, the nodal coordinates are changed with the iteration steps.Therefore,when the presented length of the strut is equal to the target length, it means the tensegrity structure reaches the desired configuration.In general,the cable force density is a positive value and the strut force density is equal to a negative number.Thereby, in order to further constrain the variation range of nodal coordinates during form-finding procedure,the force density constraint conditions are introduced in modelling process.Hence, considering the geometrical characteristic of tensegrity mechanism and force density vectors, a general form-finding model is formed as follows


2.2 | Sequential quadratic programming method and noise tolerant zeroing neural network model
In this subsection, the SQP method is utilised to solve the NCO problem (1).Hence, for the purpose of developing the form-finding model, the general form of the form-finding model which is an NCO problem (1) can be defined as

where the approximation matrixBkis introduced to replace the Hessian matrix for the purpose of reducing calculation complexity,anddkis the search direction,which is the variate of form-finding subproblem (5).However, the approximation matrixBkis not fully equal to the Hessian matrix,so the process will produce round-off error which may affect the accuracy of form-finding process.Thereby,the round-off error and external disturbance acting on the structure are regarded as noise which may affect the form-finding course.Therefore,the noise can not be neglected when designing form-finding model.Hence,as a kind of advance RNN,the NTZNN approach with outstanding anti-noise performance is proposed in the paper to calculate search directiondk.The quadratic programming subproblem(5)is rewritten as
Utilising the related Karush-Kuhn-Tucker (KKT) condition, the following equations could be defined as follows:

As a result, the discrete form of NTZNN approach polluted by noise is formed aswhere the step sizeh1andh2are positive constants,ɛkis the noise item and † represents the generalised inverse.
2.3 | Application of dynamic relaxation
In the above subsection, the search directiondkis solved through utilising the NTZNN model (14).Therefore, how to accurately obtain the nodal coordinatesXis the next crucial step of form-finding method designing procedure.As a consequence,the DR method is introduced to solve the nodal coordinates accurately.The negative gradient direction of the form-finding model (1) is formated as
In the steepest descent method (SDM), the standard search direction is equal to negative gradient direction.As for a givenXk, the SDM is performed as
whichιis a step-size.In the DR method, instead of the negative gradient direction,ωis defined as an external force acting on the nodal coordinates.According to the Newton's second law of motion-force and accelerationF=ma,the nodal acceleration is defined by
wheremis the fictitious mass matrix,Fis the external force acting on the nodal coordinates.
Similar to SDM (16), the iterative way of dynamic relaxation method is formated as
whereνis the nodal velocity,ιis the sample interval, andδis the damping coefficient.From SDM(16)and DR method(18),whenδ= 0, the DR becomes an exact SDM method.
The process of the DR method is shown in Figure 1.In order to realise the goal of finding a self-equilibrium tensegrity structure, the nodal coordinateXk+1and velocityνk+1are obtained from DR method which is combined with kinetic damping (18).When the current kineticEof the nodal coordinate reaches to the local maximum, the velocity of nodal coordinateνis set to zero for recalculating the kinetic energy.Hence,the iteration process is restart until it reaches next local maximum of kinetic energyE.By means of DR method with kinetic damping coefficient, the kinetic energyEis continued to decrease during the iteration process.Thereby, the eventual nodal coordinate result could be obtained when the kinetic energyEis smaller than the convergence tolerance or equal to zero.
The fictitious mass matrixmis set as an identity matrix for facilitating calculation.The kinetic energy is formated as
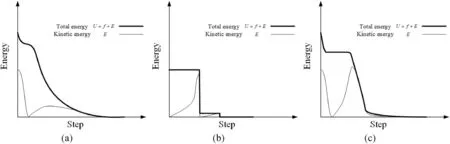
IfEk+1 Compared with the traditional dynamic relaxation method,through the calculating rule (20), it does not need to calculate unnecessaryXandν, which can reduce computational complexity and keep iterative convergence rate.When the kinetic energyEis equal to zero or less than the tolerant error,the nodal coordinateXkis the final results.Hence, Table 1 shows the process of DR-NTZNN method. F I G U R E 1 The process of dynamic relaxation method with kinetic damping T A B L E 1 The process to solve form-finding problem For the purpose of ensuring the availability of DR-NTZNN form-finding algorithm, the performances of stability, consistency and global convergence of the NTZNN model are investigated in this subsection [16]. Comparing the NTZNN withO(ι2) pattern residual error(23) and NTZNN (14), it can be drew a conclusion that, the NTZNN (14) is established when theO(ι2) pattern residual error is neglected.Hence, the NTZNN (14) is consistent with 2-order ofO(ι2) pattern residual error due to the above definitions.Moreover, the NTZNN is converge withO(ι2)pattern truncation error for ∀t∈[t0,tf] on account of the Definition 3. In this subsection, the influences of damping coefficientδto the form-finding course are discussed through three types damping coefficients.In the first place,a variate can be defined by the nodal coordinates velocity and acceleration which is written as where|.| represents the Euclidean norm, the damping coefficientδkat stepkcan be seen as a function ofθk[12], it is characterised by Three types of damping coefficients are defined in this subsection, above all, the viscous damping is defined as where const is a constant.Furthermore, the kinetic damping can be written as When nodal coordinate kinetic energyEreaches a local peak, it means that the nodal coordinates acceleration is orthogonal toν,andθis equal to 0.Moreover,before the kinetic energy reaches the local maximum,theθis greater than 0 due to the increasing nodal coordinate kinetic energyE.Besides,whenθis less than 0,it describes the process of kinetic damping.In the existing DR form-finding method, the kinetic damping is the most common and efficient coefficient[5,13].Yet,as shown in the Figure 2, the kinetic damping may cause the discontinuous characteristic curve.Thereby,for solving the discontinuity of kinetic damping,the drift damping is defined as The form-finding process can be adapted dynamically between the nodal coordinate acceleration and deceleration,which is similar to the kinetic damping.The damping coefficientδis adjusted between 1.0 and 0.9 through Equation (31), the drift damping can transform smoothly which is opposed to kinetic damping. During the form-finding course, the relationship between total energy with the number of iterations are shown in Figure 2.It shows the properties of the three damping coefficients in detail.When the viscous damping is applied in the DR method,a small amount of nodal coordinate kinetic energyEis continuously dissipated during the form-finding course.Besides, if the kinetic damping is applied in the DR method,the nodal coordinate kinetic energyEis not decreased until the kinetic energyErealised a local peak.Combined with dynamic damping and viscous damping coefficients, the drift damping has the advantages of the above two coefficients.However, in the DR form-finding algorithm design process,numerous DR algorithms use dynamic damping due to the complex structure of drift damping coefficient and the dynamic damping can satisfy the requirements of form-finding process [13]. In this section, several numerical examples and contrast simulations are proposed to verify the computational efficiency and anti-noise performance of the DR-NTZNN form-finding method. In the numerical examples,the form-finding course is polluted by noise items, in the modelling process of DR-NTZNN method, the noise includes the round-off error which is caused by approximate matrixBk, besides, in the dynamic relaxation method, in order to reduce the computational complexity ofXt*,the calculation error which is brought by the calculating rule(20),and the external interference in the actual form-finding process,these circumstances should be considered in the modelling course.Hence, an arbitrary linear noiseɛ=ψk+σis introduced in the paper.Wherekis the iteration step,ψandσare the constant coefficients.In this subsection,for the purpose of demonstrating the effectiveness of the DRNTZNN form-finding method in two-dimension space,supposing there is a hexagon tensegrity mechanism, which is consisted by three struts and six cables.The form-finding course is terminated within 2 s,the cutoff error is 10-2.Besides,the selfequilibrium configuration is shown in Figure 3.Although the hexagon tensegrity structure is a simple structure,however,the simulation result demonstrates the effectiveness of the DRNTZNN algorithm in dealing with non-linear optimisation problems which is transformed from tensegrity structure formfinding problem.Hence, the self-equilibrium structure is established even though the form-finding process is disturbed by noise.It can prove the excellent anti-noise performance of the DR-NTZNN algorithm. F I G U R E 3 The self-equilibrium status of hexagon tensegrity structure F I G U R E 2 The relationship between total energy with the number of iterations under the viscous, kinetic, and drift damping coefficients. In addition, a four-prism tensegrity structure based tensegrity robot is widely utilised in the field of tensegrity robot[33,34].Hence, a tensegrity robot is presented to verify the efficiency and calculation performances of the DR-NTZNN approach.A four-prism tensegrity system is consisted by 4 struts, 12 cables and 8 nodes.Figure 4 shows the selfequilibrium four-prism structure obtained by utilising the DRNTZNN algorithm, which could also be called as standing position of tensegrity structure [33].With the increase of iterative steps, the interference of noise item to the form-finding process is increase gradually.In the wake of increasing iteration numbers, the accuracy level of 10-2has always been maintained during the simulation process.However, in the simulation, the DR-NTZNN algorithm could cause the error converge to 10-2under the noise environment promptly and the error accuracy is improved which compared with the formfinding algorithm using dynamic relaxation method[13]. Besides,in order to further investigate the efficiency of DRNTZNN method in three-dimensional space,a hexagonal prism tensegrity structure simulation is proposed in this subsection.The self-equilibrium mechanism of the tensegrity structure is seen in Figure 5 and the cut-off error is 10-1.The proposed tensegrity mechanism is consisted by 12 nodes,6 struts and 18 cables.The simulation result shows that the hexagonal prism tensegrity structure could establish its self-equilibrium configuration though the DR-NTZNN method under the noise environment.Although the form-finding course of hexagonal prism tensegrity structure spends more time to form the selfequilibrium than the four-prism tensegrity structure, this is due to the six-prism tensegrity structure has higher structural complexity.However,the DR-NTZNN form-finding algorithm can still find the self-equilibrium configuration of the structure,which is demonstrated the effectiveness of DR-NTZNN algorithm in dealing with the form-finding problems of sophisticated three dimensional tensegrity structure. F I G U R E 4 The self-equilibrium status of four-prism tensegrity structure F I G U R E 5 The self-equilibrium status of hexagonal prism tensegrity structure Furthermore, a truncated tetrahedron tensegrity is proposed to verify the efficient of the DR-NTZNN algorithm.The truncated tetrahedron tensegrity mechanism is constructed by 6 struts, 18 cables and 12 nodes.With respect to the proposed high-dimensional tensegrity structure, although the dimension of constraint conditions are 24 × 36, the form-finding course takes 13 steps to find the self-equilibrium mechanism which can be seen in Figure 6 and the cut-off error is 10-2.In the simulation example, through adjusting the NTZNN parametersh1andh2can enhance the error precision.However, arbitrarily changingh1andh2may not applicable for the actual formfinding process.As for the NTZNN model, the values ofh1andh2have an upper bound.Therefore, arbitrarily increasing the values ofh1andh2will spend more computation time and may cause a failure to the tensegrity form-finding procedure. Additionally,tensegrity structures are widely used in the field of robots, such as tensegrity bows and spherical tensegrity robots[1,35,36].Consequently,a fusiform tensegrity robot[1]is selected to find its self-equilibrium configuration for purpose of verifying the applicability of DR-NTZNN form-finding algorithm.Figure 7 shows the geometric construction of fusiform tensegrity robot.The fusiform tensegrity robot is consisted by four struts,four cables,two springs and a actuator.Besides,the springs can be seen as cables.Thereby, the tensegrity robot contains four struts and six cables, and the actuator can be neglected during the form-finding process.Under the 10-1pattern cutoff error, the presented structure find its selfequilibrium configuration with noise polluted.In order to investigate the nature of fusiform tensegrity robot, the formfinding usually analyses the tensegrity structure that without external forces.This is the reason why the actuator is neglected in the form-finding process.The DR-NTZNN method is utilised to find self-equilibrium configuration of tensegrity robot,which is facilitated the statics and kinematic properties analyses of tensegrity structure.As can be seen in the Figure 8,the DRNTZNN form-finding algorithm successfully finds the selfequilibrium structure of fusiform tensegrity robot, hence, the self-equilibrium structure is used for subsequent investigations.Therefore, the DR-NTZNN form-finding approach has practicability in the field of tensegrity robots. F I G U R E 6 The self-equilibrium status of truncated tetrahedron tensegrity For the sake of revealing the computational efficiency of the DR-NTZNN algorithm and the superiority in the face of noise interference, two classical form-finding algorithms are proposed as comparative simulations in this subsection.First,in order to reflect the computational efficiency of the DRNTZNN algorithm, a contrast simulation between the DRNTZNN form-finding method and modified Broyden-Fletcher-Goldfarb-Shanno noise-tolerant zeroing neural network (MBFGS-NTZNN) form-finding approach [14] is proposed in this subsection.In the contrast simulation, the form-finding process are under the arbitrary linear noiseɛ=ψk+σpolluted.The MBFGS-NTZNN form-finding approach takes 49.376 s to find the self-equilibrium configuration of four-prism tensegrity structure.As a contrast,the formfinding process which utilising DR-NTZNN algorithm takes 2.399 s.The results are shown in Table 2. F I G U R E 7 The mechanism structure of fusiform tensegrity robot F I G U R E 8 The self-equilibrium status of fusiform tensegrity robot For the MBFGS-NTZNN algorithm, in spite of the algorithm establishes an efficient objective function,and the formfinding model can effectively express the physical properties of the tensegrity structure,which means stiffness matrix of the structure is positive definite during the form-finding procedure,hence,the tensegrity structure is in a stable state.However,the Jacobian matrix of the objective function is considered in the modelling process.Although the dimensions of the Jacobian matrix may not affect the computational efficiency for twodimensional structures.Nonetheless, as the structures get more complex, the dimensions of the Jacobian matrix will become extremely large, which may affect the computational efficiency seriously. Furthermore, an extra comparison is proposed between the DR-NTZNN method and the modified DR form-finding approach to demonstrate the importance of anti-noise functionality [13].As for a two-dimension hexagon tensegrity structure, the modified DR method take 3.4346 s to establish the self-equilibrium configuration under the noise environment.In the previous simulation result, the DR-NTZNN form-finding approach spends less than 2 s to establish the same self-equilibrium structure and the DR-NTZNN method takes 2.399 s to find a more complicated structure under the same noise interfered.The results are shown in Table 3.It can draw a conclusion that,the modified DR method has powerful computational efficiency, yet, the efficiency of modified DR algorithm will be weakened when encounter the noise interference.By means of the proposed contrast simulation, it can prove the importance of noise tolerant functionality of DRNTZNN method during the form-finding course. In summary, through two groups contrast simulations, the DR-NTZNN algorithm shows the calculation and anti-noise performances which compared with the existing classical form-finding algorithm.As a kind of advanced RNN, the NTZNN model has high efficiency in handling the non-linear optimisation problems.Through two-dimensional and threedimensional tensegrity structures, and high-dimensionaltensegrity structure simulation results,it demonstrates the DRNTZNN form-finding algorithm is effective when dealing with the tensegrity form-finding problems.In addition,the DRNTZNN algorithm can still find the self-equilibrium tensegrity structure under the noise interference, which can prove the NTZNN algorithm has excellent anti-noise performance during the form-finding course.Furthermore,the fusiform tensegrity robot application illustration example verifies the effectiveness of DR-NTZNN algorithm in the application field,which greatly expands the application scope of DR-NTZNN algorithm.Eventually, two groups of contrast simulations prove the computational efficiency of the DR-NTZNN algorithm and the excellent anti-noise performance which is compared with the traditional DR form-finding algorithms. T A B L E 2 The form-finding results of different form-finding methods T A B L E 3 The form-finding results of different form-finding methods In this paper,a high efficiency DR-NTZNN method has been proposed for solving form-finding problem which is based on determining NCO problem.An efficient and general model is constructed to deal with the NCO problem combined the SQP method and NTZNN algorithm which gives the anti-noise performance to the DR-NTZNN method.Moreover, the DR method with kinetic damping could solve the nodal coordinates vector with high iteration speed and accuracy.Eventually,several tensegrity simulations and contrast examples have been proposed to show the practicability and precision of the presented DR-NTZNN form-finding method which is compared with the classical form-finding methods.In the future,how to construct a general dynamics relaxation form-finding model for engineering applications is the main concern. ACKNOWLEDGEMENTS The work is supported in part by the National Natural Science Foundation of China under grants 61873304, 62173048,62106023 and in part by the China Postdoctoral Science Foundation Funded Project under grants 2018M641784 and 2019T120240, and also in part by the Key Science and Technology Projects of Jilin Province, China, under grant 20210201106GX, and also in part by the Changchun Science and Technology Project under grant 21ZY41. CONFLICTS OF INTEREST The authors declare that there is no conflict of interests regarding the publication of this paper. DATA AVAILABILITY STATEMENT Data available on request from the authors. ORCID Zhongbo Sunhttps://orcid.org/0000-0003-1287-2917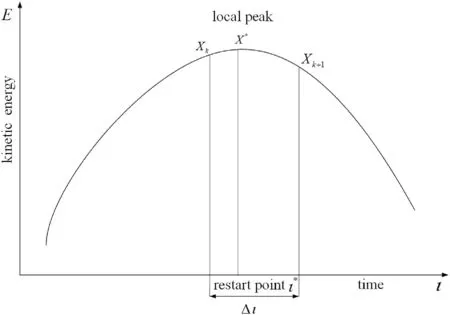

3 | THEORETICAL ANALYSES
3.1 | The analyses of the noise tolerant zeroing neural network model


3.2 | The analyses of damping coefficient
4 | NUMERICAL EXAMPLES
4.1 | Two‐dimensional and three‐dimensional examples


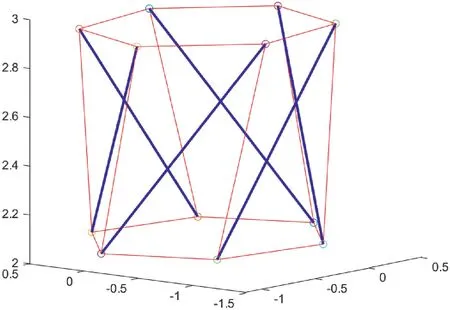
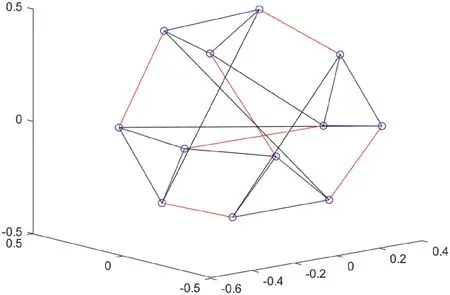
4.2 | The contrast simulations




5 | CONCLUSION
 CAAI Transactions on Intelligence Technology2023年3期
CAAI Transactions on Intelligence Technology2023年3期
- CAAI Transactions on Intelligence Technology的其它文章
- Fault diagnosis of rolling bearings with noise signal based on modified kernel principal component analysis and DC-ResNet
- Leveraging hierarchical semantic‐emotional memory in emotional conversation generation
- Forecasting patient demand at urgent care clinics using explainable machine learning
- A federated learning scheme meets dynamic differential privacy
- SRAFE: Siamese Regression Aesthetic Fusion Evaluation for Chinese Calligraphic Copy
- Wafer map defect patterns classification based on a lightweight network and data augmentation
