A federated learning scheme meets dynamic differential privacy

Shengnan Guo| Xibin Wang | Shigong Long | Hai Liu | Liu Hai |Toong Hai Sam

1State Key Laboratory of Public Big Data,College of Computer Science and Technology,Guizhou University,Guiyang,China

2School of Big Data,Key Laboratory of Electric Power Big Data of Guizhou Province,Guizhou Institute of Technology,Guiyang,China

3School of Information, Guizhou University of Finance and Economics,Guiyang,China

4Faculty of Business and Communication,INTI International University,Nilai,Malaysia

Abstract Federated learning is a widely used distributed learning approach in recent years,however,despite model training from collecting data become to gathering parameters, privacy violations may occur when publishing and sharing models.A dynamic approach is proposed to add Gaussian noise more effectively and apply differential privacy to federal deep learning.Concretely, it is abandoning the traditional way of equally distributing the privacy budget ∊and adjusting the privacy budget to accommodate gradient descent federation learning dynamically,where the parameters depend on computation derived to avoid the impact on the algorithm that hyperparameters are created manually.It also incorporates adaptive threshold cropping to control the sensitivity, and finally, moments accountant is used to counting the ∊consumed on the privacy-preserving,and learning is stopped only if the ∊total by clients setting is reached,this allows the privacy budget to be adequately explored for model training.The experimental results on real datasets show that the method training has almost the same effect as the model learning of non-privacy,which is significantly better than the differential privacy method used by TensorFlow.

K E Y W O R D S data privacy, machine learning, security of data

1 | INTRODUCTION

With big data is exploding as more and more information is collected and stored daily,it is expected that the big data-driven artificial intelligence (AI) will soon be applied in all aspects of our daily lives from the smallest means of transportation for everyone to travel to the largest medical systems for groups and future space exploration.As far as known that valuable information can improve the quality of services provided by data providers and can also be mined from these massive amounts of data.However, data is considered a sensitive element, especially when it is used to characterise users' features, such as spending records and clinical data.Therefore,Google proposed Federated Learning (FL) in 2016 [10] to mine and train the data effectively while protecting privacy.The advantage of federated learning is that instead of exchanging personal data with a central server, the data is left locally on the per client for training, thereby protecting the client's data from being eavesdropped on by attackers.

However,federated learning can only guarantee to a certain extent that the initial data will not be leaked.The data transferred by federated learning to avoid the initial data out of the database is usually irreversible model information, such as weight parameters of neural networks and information gain in the decision tree.But, as stated in [2, 30], once the federated trained model is valid,then it is inevitable that the transmitted data will leak the information of the raw training data inevitably.When the federated model with completed training is deployed outward via APIs [3], it is valuable confidential information for the participants besides ensuring the privacy and security of the initial data.Several solutions have been proposed to address these issues, for example, using the basic primitives in cryptography, the privacy protection can be achieved, where the main cryptographic strategies applied in federated learning include obfuscated circuits [11], inadvertent transmission [12], secret sharing [13], and homomorphic encryption [14].Another commonly used technique is used Differential Privacy (DP) that is proposed by Dwork [1, 6] in 2006.Unlike a traditional privacy protection approach, DP defines a strict attack model independent of background knowledge that not only gives a quantitative representation of the extent of privacy leakage but also enables the protection of individual privacy information while learning, and it has been used in practice, such as the 2020 U.S.Census where differential privacy was used to protect the confidentiality of individuals [45] at the first time.

At present,some scholars have already combined federated learning and differential privacy, but there is still a large communication cost problem due to the iterative nature of federated learning and the complexity of the model.To alleviate the communication bottleneck of federated learning,one of the current research directions is to focus on reducing communication cost, and improving model performance and generalisation,such a differential privacy model(FL-MAC-DP)to multi-access channel federated learning, has been proposed[16] for balance between security needs and communication efficiency in federated learning, which allows users to communicate through the multi-access channel FL (FL-MAC)model [15].Another research direction is to improve the application scenario and generalisation ability of federated learning to apply federated learning to unbalanced devices and data under the premise of privacy guarantee and be deployed and set up across devices without compromising the effectiveness and precision.Although there have already some federated learning technologies based on differential privacy,however,they are still facing challenges in terms of protection efficiency, protection quality, and availability of privacypreserving.For example, some federated learning models that fixedly add noise can cause the learning process to be greatly affected, resulting in slowing down the rate of the convergence process.And adding noise to parameters in the Deep Learning training procedure is equivalent to“surgery on the heart”as illustrated in[41],which may result in a significant decrease in the effectiveness of the model or even make it unusable.Thus, the self-adjustment ability on the federated learning model and balance between privacy and usability are still bottlenecks in this field.

A federated learning technique was proposed in this paper that allows users can add perturbation dynamically.Among them,dynamic mainly refers to two methods,on one hand,the privacy budget is assigned dynamically,and on the other hand,relevant parameters such as the clipping threshold in deep learning are selected dynamically, which together enable us to generate higher quality federal learning models with a fixed privacy budget.

In summary, the main contributions of this paper are as follows:

i.A DP algorithm with dynamic privacy budget allocation is proposed that can be applied in the federated learning model, where the added noise scale can be adjusted dynamically during model training, and privacy loss is tracked in real-time using moments accounting methods.

ii.When using differential privacy,an optimal Gaussian noise[17]is used with analytic correction and optimal denoising,which solves the problem that the variance formula of the original mechanism is far from rigorous in the high privacy regime (tends to 0) and the low privacy regime (tends to infinity).And by constraints such as minimax risk, it is proved that upper bound and lower bound can match or their gap is a constant, that is, this statistical method is minimax optimal or nearly minimax rate optimal.

iii.Based on the federated learning depth model taking a hierarchical clipping threshold, a modified gradient descent method is used in this paper to carefully adjust and inject noise in each iteration.This approach can improve the usability of the model more effectively with limited privacy costs.

iv.The definition of differential privacy is strictly satisfied in the process of adding noise and evaluating our method on three real datasets MNIST,Fashion-MNIST,and CIFAR10 and demonstrates that the improved technique provides higher usability and can be used to build a privacy federal learning model.

The rest of this paper is organised as follows.Related work is reviewed in Section 2.The background of differential privacy and federated learning is presented in Section 3.Section 4 proposes an algorithm for dynamically adapting privacy budgets and conducting them.Section 5 contains experimental results on a real dataset and concludes with a summary in Section 6.

2 | RELATED WORK

In this section, we provide background on differential privacy and introduce some prior work on privacy-preserving mechanisms applied to data mining,machine learning,deep learning,and federated learning.

To solve the shortcomings of federated learning in terms of privacy security,several algorithms have been proposed one after another.Among them, Google proposed the most common algorithm in federated learning research nowadays,which was named the FedAvg algorithm based on the stochastic gradient descent optimization algorithm [18].Li et al[19] proposed a Fed Prox algorithm that can solve the heterogeneity problem of federated learning based on the Fed Avg algorithm.Wang et al[20]proposed a Fed MA algorithm that is an improvement over the previous two algorithms for heterogeneous users.Although all these algorithms provide some privacy guarantees for federated learning, researchers often need to apply cryptographic strategies and DP approaches for privacy protection because none of them are formal enough.The most intuitive approach to protecting privacy is the cryptographic approach among them, which mainly utilises homomorphic encryption [14] and secures multi-party computation [21] to protect each user's gradient privacy information in the process of gradient descent.

Zhu et al.[4]proposed a new reconstruction attack scheme and named it Deep Leakage from Gradients(DLG).The DLG attack proved that an attacker could recover the initial data by analysing the gradient information.To protect the privacy of the gradient and enhance the security of the system, extra homomorphic encryption is applied in [5].But cryptographic methods usually trade efficiency for privacy,which may lead to become very inefficient in computation and communication,especially on models that require a large amount of communication like federated learning; it appears particularly sharp.The proposed differential privacy [6] points out an alternative path for researchers.

The research studies on combining traditional ML with DP algorithm include DP principal component analysis(PCA)[7],etc.And there are numerous studies combining DP with Deep Learning techniques,such as Shokri et al.[8]and Hayes et al.[46],proposed a distributed selection stochastic gradient descent algorithm,and Abadi et al.[9]proposed a novel differential privacy stochastic gradient descent algorithm.They also proved that the method that reduces noise accumulation by tracking is also fit for the random sampling Gaussian mechanism and can obtain a smaller accumulated privacy loss than before.The idea of RDP(Renyi DP)such as[9]was proposed at the same time by[32].Essentially,the fundamental ideas of[9,32]are the same,so researchers now use them collectively as one sort.

Papernot et al.[23] proposed a generalised approach to protect the privacy of machine learning data based on the idea of knowledge aggregation and migration—The Privacy Aggregation of Teacher Ensembles(PATE)scheme,which applies to any model that includes non-convex Deep Learning models,and its shortcoming that privacy is reduced accompanied by the possibility of leakage risk becomes larger.In addition,if there is a correlation between different records, DP can only achieve a single point of privacy protection, and the attacker still gets privacy from those who meet DP requirements.Then, Phan et al.[22]developed an adaptive noise addition method,that is,by perturbing the neuron affine transform and loss function to adaptively inject noise into the features based on the effect of each output on the result.Also, there are a few extensions for combining Federated learning and Differential Privacy, for example, Choudhury et al.[35] proposed a privacy-preserving approach based on LDP (local differential privacy) to learn effective personalised models on distributed per client data while meeting different privacy security needs of it.

The F-DP was proposed by Dong et al.[42], and the analysis of the precise composition becomes more facilitate for private algorithms.Hence, it is applied by much research in deep learning.For example, [43, 44] are some related applications of F-DP.However,although this algorithm is claimed to push the concept of differential privacy easier to interpret, it has gradually presented difficulties when the mechanism needs to combine,and which is not performing as well as the method proposed by [9, 32].

Scholars have not only carried out cross-fertilized the field of machine learning field and DP but there are also even plenty of studies on DP protection algorithms themselves.The Gaussian mechanism used in the general literature at present is generally constructed based on [1, 24], while the Laplace mechanism is constructed based on [6], and the exponential mechanism is introduced in[25].Similarly,the CDP[31],RDP[32], and truncated CDP [33] have been proposed recently.And some novel privacy notions have also been studied, such as the truncated Laplacian mechanism [26], the staircase mechanism[27,28],and the Podium mechanism[29].Ref.[17]improved Gaussian mechanism according to analytical calibration, concluded optimal Gaussian mechanism for (∊,δ)-differential privacy, which means the noise amount is the least among Gaussian mechanisms.Then,[36]contributes to further analysis according to [17]; it analysed that the condition of(∊,δ)-differential privacy has not been realized in some previous studies and fixes long-time misuse of Gaussian mechanism in the literature by proposing closed-form expression for upper bounds forσDP-OPT.

In summary, it has further extended and deepened in this study, applying some results to federated learning when performing local processing and sending training parameters to the central server, and improving the way of perturbation to improve the usability of federated learning while protecting privacy.

3 | PRELIMINARIES

In this section, we provide some important definitions and theorems on differential privacy and federal learning.

3.1 | Differential privacy

Definition 1((∊,δ)-differential privacy [1]).A randomized algorithm M satisfies (∊,δ)-differential privacy if for any two neighbouring datasets D and D′that differ only in one record,and for any possible subset of outputs S of M, it has

D and D′are adjacent if D′can be obtained by adding all the items associated with a single user from D.P[⋅]denotes the probability of an event.Ifδ=0, M is said to satisfy pure ∊-differential privacy, andδaccounts for the probability that plain pure ∊-differential privacy is broken.

In this paper, the results do not rely on how neighbouring datasets are specifically.After the definition of neighbouring datasets, global sensitivitySG(f) is defined as

However,the Classical Gaussian Mechanism(referred to as CGMDP)has been fairly abused(e.g.,in[37,38]).∊≤1it should be preferred by the initial application of DP,but∊>1but abuse often happens when the concept of DP is used in many other fields,for example,in machine learning.Even in[36],∊>1meant G(δ)is some positive function,and it also indicates the noise added according to CGMDP is not enough to meet the differential privacy definition equals the privacy mechanism is leaking privacy at this moment.Theorem 2 is proposed by[17]for dealing with it.

Theorem 2(Optimal Gaussian mechanism for(∊,δ)-differential privacy DP-OPT).For any δ∊(0,1)and∊>0.A randomized algorithm f hasl2-sensitivity∆,and it has the Gaussian output perturbation mechanism M=f add noise(σ),noise～ (0,σ2I),M is(∊,δ)-DP if and only if:

Some other related theorems and definitions have been proposed as follows:

Definition 2 (Privacy Loss)If there are two neighbouring datasets D and D′, and mechanism M has the density of the random variable:Y=M(D)aspM(D)(y).Then,the privacy loss function of M on two neighbouring databases D and D′is defined:

Remark1 (Moments accountant (MA) [9]) If there are two neighbouring datasets D and D′, the moment generating function of randomized algorithm M at the value λ:

3.2 | Federated learning

As we know,although it is not transmitting raw data directly during the process of federated learning, the model is in a vulnerable situation when aggregating the model parameters from each federated learning client to the central server node.A series of protection methods have been proposed for the federated learning model to solve such security issues,DP is used in this paper because of two reasons, one is to learn the complexity of the federated learning model and the other is to synthesise the issues arising from the use of different security protocols designed by various security tools, such as high computational, communication overheads, model reversal attacks,inefficient training, etc.Also,the “Federated Averaging”algorithm is used in this paper to address the challenge that client data may be non-IID,unbalanced,and massively distributed and to achieve user-level DP for federated learning models.

3.3 | Federated learning with differential privacy

There are three kinds of ways to perturbation in the machine learning process by using DP protection generally: the output perturbation method, the target perturbation method, and the gradient perturbation method.Both the output perturbation method and the target perturbation method require the calculated result about an upper bound on the sensitivity.The gradient perturbation method is generally used in deep learning because it is almost impossible to compute an upper bound on the sensitivity for a complex algorithm such as a convolutional neural network.Thus,the federated learning model always chooses the gradient perturbation method in DP,which depends on a convolutional neural network that is most regularly used in the model itself.The general framework is shown in Figure 1.

Compared to traditional machine learning, deep learning requires more communication and weight to make the performance higher,but it will result in more privacy passed in the federated learning process.Also, note that protecting data in the process of learning a model for federated learning differs significantly from the normal application.In deep learning,it is imperative not to overfit the data, which means some deviations can occur in the training procedure.For researchers,the focus is on how to improve the usability of the model more efficiently with a fixed privacy budget.From this point on,the following work have done.

4 | THE PROPOSED METHOD

The previous section demonstrates that the allocation of privacy costϵbrings challenges to both the effectiveness and security of the model.Therefore,in this section,the algorithm model named as Dynamical Differentially Private Federated Learning (D2PFL) was presented to improve the model convergence speed, which is detailed in Algorithm 1, Algorithm 2, and Algorithm 3.

The learning approach involves two main steps:

i.Adding perturbations in each learning round and judging whether the added noise is too much by the direction of gradient descent, to adjust the noise amount.

ii.Adaptively change the threshold value of the cropping gradient when calculating the amount of noise to better adapt to the process of model learning.

In the followings, it will get a more detailed introduction.

4.1 | Allocate a privacy budget dynamically

Algorithm 1 (D2PFL) Dynamical Differentially Private Federated Learning Input:Training dataset,X= x1,x2…xn｛ ｝;Loss function, L(w)= 1NΣ L wi,xi( ); add noise parameters, σI,σC,σmax; learning rate, α;batch size, B; clipping threshold, C; the budget of the privacy,∊I,∊C,∊max;total rounds of global training, E; max numbers of local training, T; Number of local clients participating in the training, K;Output: model parameters, wi; Using moments accountant computing privacy loss;1.Initialise wi randomly;2.for t ∊E do e ←e+1 do 3.Take a random sample K and each Client does:4.for k ∊K and t ∊T and ∊I ≥0 do 5.for each i ∊Bt compute gi ←∇wtL wi,xi( )do 6.Update clipping threshold C from Algorithm 3 7.gi ←gi/max(1,■■gi■■|2/C),save gi as gI( ),save ～gi as gC,9.∊I=∊max-∊I,10.if ～gi is not right direction then 11.change noise to parameters σC 12.～gi ←gI+N 0,σ2CC2I 8.～gi ←gi+N 0,σ2IC2I( ),∊I=∊max-∊c 13.if ～gi still not right direction then 14.～gi ←gC ,∊I=∊max-∊I 15.end if 16.gt ←Σ ～gi 17.end if 18.Updating model parameters wi 19.end for 20.return parameters wi to CES and CES updating model 21.CES broadcasts global noised parameters and opens the next round 22.end for 23.end for

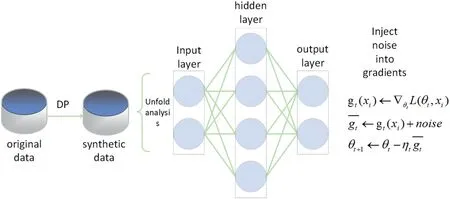
F I G U R E 1 Gradient perturbation in federated learning

The amount of Gaussian noise level is added based on the allocated given privacy budget in each iteration,and it also has an impact on the availability and privacy of the algorithm.Therefore,scholars have been doing studies related to how to allocate the privacy budget more reasonably.The authors in ref.[39]believe gradient-based algorithms that can be improved by a more careful allocation of privacy budget per iteration,propose a private gradient-based algorithm in which the privacy budget and step size for each iteration are dynamically determined at runtime based on the gradient obtained for the current iteration.The authors in ref.[40]allocate privacy budget adaptively based on trends in real-time data on social networks.However,the two are designed for applications in special scenarios,which are not applied to the federated learning model with high communication overhead or be used in iterations multiple times intended to learn deep model.D2PFL was proposed for dynamic allocation of DP budget in federated learning based on the idea that the amount of added noise can be gradually reduced accompanied by the gradual convergence of the federated learning model learning process.This implies a gradual shrinking of noise parameterσ.Unlike in[39],the algorithm is not required that the model must hold the correct descending direction after adding noise in the learning process, and the parameter is changed at most once in local training.

In D2PFL,which does not require access to the initial data and the amount of noise decayed gradually with the training procedure.Although a complicated iteration process can be designed,Algorithm 2 amended noise parameters in order not to increase the complexity of the whole algorithm as well as to increase the usability of the algorithm in two ways.

Algorithm 2(D2DP)Dynamical differentially private budget ∊Input: gradient, ∇f; privacy budget, ∊I,∊C and correspond to add noise parameters,σI,σC (firstly means initial one and then the changed one); current iteration, t;polynomial parameter, γ; The superscripts t and t+1 represent the number of current iterations Output: noise parameters, σ;1.Initialise wi randomly;

2.In the t iteration,3.if ∇f+N 0,σtICI( )is not right direction then 4.①simple Polynomial method 5.∊tC =∊tI+(1+t)γ 6.②complicated Polynomial method(exponential form)7.P(t)= ∊t+1I P(t)+(∊tI-∊t+1I )P′(t)∊t+1( from combine ∊tI and ∊t+1 I + ∊tI-∊t+1I )I 8.Where P′(t)=∇f(wt)+N(0,(σt+1I -σtI)2C2I)P(t)=∇f (wt )+N 0,(σt( )2C2 I)Let P(t)=∇f(wt)+N(0,(σC)2C2I)9.∊t+1 I I =∊tIeγ,get γ iteratively, the details can be found in Lemma 1 the Appendix 12.if ∇f+N 0,σ2CC2I( )is still not pointing in the right direction that means this change did not work,then out of the loop and open the next one.then 13.get ∊=∊tI and σ= s+ ——————--s2+∊(√)/∊√---2 14.s =■——————————————————————--ln 2/(————————-16δ+1√ -1)15.end if 16.if ∇f+N 0,σ2CC2I( )is right direction then 17.in t+1 epoch, get ∊from ①or②and σ= s+ ——————--s2+∊)/∊√---2 18.end if 19.end if(√

The first way of Algorithm 2 is a simple function for computation of privacy budget, and it adjusts parameters flexibly to the strategy in training progress.The way that using(1+t)multiplied by hyper-parameterγenables the amount of noise reduced along with increasing iteration times.This is also consistent with the gradual convergence of the model.A method for selecting hyper-parameterγis to experiment with alternatives in training the model about m times and choose the highest data quality alternatives finally.However, this method also did not chosen in the end because the availability of the algorithm in the real scene is greatly reduced due to the complexity and the traffic.In this paper, a value selection scheme satisfying the differential privacy is adopted:the dataset is divided into training,validation,and test in the proportion of 8:1:1, there are at most 0.8Nkinds of hyper-parameters (Nis the total amount of dataset), and the corresponding hyperparameters of training rounds with high accuracy are selected with an exponential probability for testing in the verification and test.As a result,γis estimated to be 0.1 roughly through experimental calculation in this paper.

Gaussian noise parameters added in both are obtained according to Lemma 1 [36] as follows:

Lemma 1(Improved Optimal Gaussian Mechanism for(∊,δ)-DP)From Theorem 2,with0<δ<0.5,it will add Gaussian noise to each dimension of a query withl2-sensitivity∆,for σ is given by:

Lemma 1 is an improvement on Theorem 2, which may consume too much memory and time complexity since an iterative process, and it exchanges a certain accuracy for avoiding higher computational complexity.When using the Remark 1 MA method, a suitable relationship can be found between ∊,δ,σand the number of iteration rounds T satisfying a certain relationship.In this paper, instead of fixing the number of iterations, the total privacy budget ∊totalconsumed is given, and the initial ∊value is given at the initial iteration,and then the correspondingσvalue is calculated using Lemma 1.This approach can avoid extreme cases during training,such as when the threshold is reached in 1 round of local training,and the added noise cannot satisfy (∊,δ)-DP.

4.2 | Adaptive gradient clipping

When using a convolutional neural network as the target of deep learning,it is necessary to consider adding noise in per-layer in the federated learning model with DP.Each hidden layer and input layer affects the final model parameters;it has been caused by not only using feedforward propagation in deep learning but also using feedback propagation to train the model;t thus perlayer must be perturbation.All clients participate in training the same model iteratively together and starting with the same initialisation parameters, which is a natural opportunity for performing collaborative training.The gradient clipping threshold is an important parameter that affects the effective gradient learning process,and it becomes data sensitivity as one parameter of how to add noise.

In almost all literature,setting the gradient clipping threshold in adding noise is a fixed hyperparameter value,for example,in[9].But in many practical applications, gradient parameters in per-layer of a neural network differ significantly,that is,the most value of gradient in the bias layer tends to be 0,while the value of gradient in the weight layer is much larger than 0.This difference led to a contradiction:if it uses a unified clipping method,then the convergence rate of the model will be slower because the gradient of a few weight parameters is added too much noise.Correspondingly, if the gradient clipping on each parameter is performed separately, this can lead to consuming more privacy budget and bring a lot of complexity to the overall algorithm although it can reduce the overall noise scale.

Based on the above-mentioned reasons,it does not choose a unified approach to prune gradient in this paper but use an adaptable algorithm ACDP on gradient threshold selection for per-layer in the convolutional layer.Thus, it can avail itself of the full range of model characteristics that are in the network hierarchy without bringing too much complexity to the whole algorithm.At the same time,since it is pruned for per-layer as well as brings changes in sensitivity,the algorithm produces the overall privacy loss measurement with more precision by pursuing the privacy budget with the MA mechanism, which reserves more space for the model training and gain more usability for the model.

The ACDP Algorithm 3 as follows:

Algorithm 3 (ACDP)Adaptive gradient clipping in differential privacy Input: total rounds of training, E; local training epochs, T; current iteration, t;Name of the current layer, name; Maximum/average clipping threshold, Cmax, Cavg; The size of the batch, B; The superscripts t and t + 1 represent the number of current iterations;Output: The value of noise that needs to be added to the layer; and gradient clipping values;1.In t iteration, add noise layer by layer,ep.2.if In t iteration, add noise layer by layer, (ep.name = layer_input.weight)then 3.Compute Ctavg = 1BΣ i 4.if Ctavg >Cmax then 5.Ctavg=Cmax 6.end if■■|g (xi )||2

7.return σti w =σ*Ctavg 8.end if

In previous applications,in order to obtain the appropriate gradient threshold, it will be assumed that there exists a small batch of public datasetDpubthat can represent the statistical features of the private datasetDpri.By pre-training the model onDpub, an approximation about the model gradient can be obtained,and then the average value is calculated to estimate a reasonable threshold C.Alternatively, a simple value taking method is adopted directly:the average value of the gradient of a batch of samples in each training round is taken as the clipping threshold, but one drawback of this method is that if there is an abnormal sample, it will make the threshold C too large leading to adding too much noise.Therefore,Cmaxis set in Algorithm 3 to constrain the highest point of the threshold.

In Algorithm 3, although it calls parameters (i.e., gradient∇g(xi)) from the data source directly applied to computation,the clipping thresholdCtavgis not directly returned.Instead,it is used to calculate the amount of noise,andσwould be returned.This is due to that the l2-norm shifts with the gradient clipping threshold, which, according to the definition of sensitivity and differential privacy,thisaffectsthe amount ofnoise addedineach iteration round in moments account.And so,the convergence speed can be improved byevaluating hierarchical gradients of the model separately and return values, this method are used for further improvement over the availability of federated learning.

4.3 | D2PFL: Dynamical Differentially Private Federated Learning

In this paper, Algorithm 2 and Algorithm 3 are used in combination and Algorithm 1 is introduced as the Dynamic Differential Private Federated Learning (D2PFL) algorithm.According to Theorem 2,the privacy-loss random variables in the algorithm are proportional to the number of iterations.

To analyse privacy, our algorithm needs to calculate an overall privacy budget spent for the entire federation learning model, and since differential privacy algorithms are combinatorial, which is shown in Theorem 3, the privacy budget consumed by machine learning can be combined by different ways as follows.

Theorem 3(composition)Suppose that in machine learning,there are T steps consisting of each step is(∊,δ)-DP,then there are four ways of combining the following:

In Theorem 3, when Gaussian perturbation algorithms with different training rounds use MA independently of each other.But there are two improved algorithms D2DP and ACDP proposed as 4.1 and 4.2 used for thetth training round, which are not independent in this paper.The most used SGD algorithm in machine learning is applied in D2DP, then takes into account both the gradient descent direction and the gradual refinement of noise addition,and finally dynamically changes the privacy budget consumed in each training round.Meanwhile, ACDP performs adaptive gradient threshold cropping for the same batch of samples,so although these two are mutually independent methods,they are doing successive operations on the same batch, so their effects cannot be simply summed up as independent.Therefore, Theorem 4 is introduced as follows:

5 | EXPERIMENTAL EVALUATION

In this paper, after adopting the improved D2PFL privacy algorithm,a lightweight federation learning is proposed with the differential privacy-preserving algorithm that does not affect the training, where each client only trains locally and submits the protected parameter data to the central server.This algorithm provides some improvement in computational complexity compared to traditional methods and is not taken into account since the SGD algorithm executed locally by the user is a generic step in federation learning.

5.1 | Experimental setup

Three datasets were used for evaluation.MNIST is a public image dataset including handwritten digital images of 28 × 28 pixels with 60,000 samples.Fashion-MNIST is an image dataset for fashion items,which is more complex than MNIST and can be considered as an enhanced version of MNIST.It covers frontal images from 10 categories with a total of 70,000 different items.The size, format, and training/test division of Fashion-MNIST are the same as the original MNIST.Both are divided in the ratio of 60,000/10,000 for training test data and the content is 28 × 28 grayscale images.Cifar10 has the same size and training/test division as MNIST and Fashion-MNIST,the difference is that it contains 32 × 32 colour images.The above three datasets are all 10 classification machine learning sets, the models differ but have the same result.MNIST and Fashion-MNIST use our own designed MLP and CNN networks, and Cifar10 uses the resnet18 network model.

The parameters of the experimental setting vary slightly depending on the dataset and also vary in settings when data need to be compared.The learning rate is 0.01 at the beginning,λis usually no more than 100 in practice and it is enough to computeα(λ)forλ≤32 in this paper.In the D2DP first simple Polynomial method, the gamma value is set to 0.1 as a hyperparameter.The optimiser used in training is SGD.In the D2DP second complicated Polynomial method, the gamma value is calculated based on the given previous round ∊.In both methods,δis set to 10-5, the cropping threshold is set to a maximum ofCmax=8, and 10% of the clients in federated learning are randomly selected for training (total is 100), as different values of these parameters do not have a strong impact on the results.

There are three datasets that were used for evaluations,summarised in Table 1.

The D2PFL is implemented in Python.Experiments are performed on a workstation running Windows 10 professional with a 3.2 GHz CPU i7-8700K,16 GB RAM, and NVIDIA Titan X GPU card.Source code is available upon request.

5.2 | Results with image datasets

Figure 2 shows the accuracy of D2PFL and others on the MNIST test set.As done in previous work, the total privacy budget ∊totalcannot exceed 5.To facilitate the calculation, the value of initial epoch ∊for each round of local training on the client-sided is set to 0.8,regardless of the setting of ∊total.The federated learning model used in MNIST is a self-built MLP(multilayer perceptron),the loss function is CrossEntropyLoss(cross-entropy), and the optimization algorithm is SGD.The X-axis corresponds to the change in the number of global training rounds,and the Y-axis corresponds to the accuracy of the test set.

It was noted that both the method non-D2DP,which does not use dynamic differential privacy assignment, and the method non-ACDP, which does not use adaptive threshold cropping, have almost all lower correct rates on the test set than D2PFL (with abrupt changes in some places).The red line is pure federated learning without any DP, the blue line is D2PFL,the green line is D2PFL without D2DP,and the black line is D2PFL without ACDP.In Figure 2, the non-D2DP algorithm distorts some parts of the curve and is more correct than D2PFL algorithm, which is also due to the characteristics of deep learning,which means that the noise added in each round does not necessarily make training results worse.Although there are a few times when the non-D2DP algorithm performs better, the curves of both the non-D2DP algorithm and the non-ACDP algorithm are not smooth enough in terms of the process, while D2PFL is relatively more stable.

As training progresses, the accuracy produced by the FL model with DP should resemble the pure FL model.In Figure 3, PFL (without adding any noise), D2PFL, and TDP(using TensorFlow own DP algorithm) are compared.Within the global iteration epoch = 100, the D2PFL algorithm converges slightly slower than PFL due to the dynamic addition of noise and then converges to almost the same correct when the global iteration training rounds reach 100.In contrast, the convergence speed and the training model of TDP are far less effective than the D2PFL algorithm, which also indicates that our algorithm is almost consistent with the effect of the machine learning algorithm without privacy protection, and TDP is much lower than that.

T A B L E 1 The datasets used in experiments

In Figure 4a,the time required to train several algorithms for 100 epochs on the MNIST dataset is compared; the D2PFL algorithm takes about the same time as the non-D2DP algorithm,the non-ACDP algorithm,and slower than the PFL with the TDP running time is quite long.In Figure 4,the comparison is the time required to train one hundred rounds for the D2PFL algorithm and the PFL algorithm in three different datasets,that is, MNIST, Fashion-MNIST, and Cifar10.From the above comparison, it can be seen that the convergence speed of the D2PFL algorithm is always slower than PFL that is the machine learning without privacy protection due to the use of DP noise addition,and the more complex the model build(resnet18 used in the Cifar10, mlp used in MNIST), the longer the timeconsuming.

In Figure 5, it can be visually seen that the time consumed increases significantly as the privacy budget increases.This is due to the D2PFL algorithm is used.The privacy budget of the first round is fixed at ∊inital=0.8, and the moments accountant method of Remark 1 is used to calculate whether the total privacy budget value X ofq×Nepochs (qis the sampling probability) exceeds ∊total, instead of the traditional federated learning algorithm with a fixed number of local training and averaging per epoch, that is,∊1=∊2=…=∊N=∊total/N.So, a larger total privacy budget value means that the rounds of local training sessions may be higher.This approach not only uses the privacy budget more effectively but also enables one to adjust the privacy budget value according to the demand, thus affecting the number of training rounds and improving the effectiveness of machine learning.

In Figure 6,the comparison is between the correct rates of Fashion-MNIST on the test set when ∊totaltakes different values.It can be seen that the difference of ∊totalleading to the number of initial of global training is different,and also leading to different starting points of correctness.After a total of 50 rounds of global training,they tend to be the same,but still can be seen to be consistent with the intuition that the correctness rate is slightly higher for a large privacy budget.

F I G U R E 2 Comparing the correctness of the algorithm D2DPL with itself(without dynamic privacy assignment)and with itself(without adaptive gradient cropping)on the test set for the MNIST dataset,the graphs of rounds 10–25 epochs are enlarged in the figure,and it can be seen that neither non-D2DP nor non-ACDP is as stable as D2DPL (although there are sometimes when the correctness may be the same)

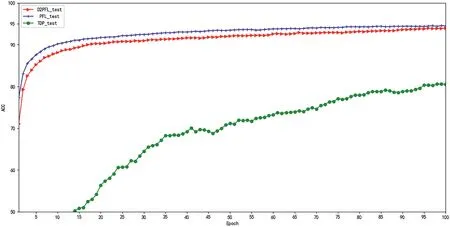
F I G U R E 3 On the MNIST dataset,the algorithm D2DPL is compared to the pure federal learning(PFL)without any perturbation,and to TensorFlow's own privacy module (TDP), comparing the accuracy on the test set

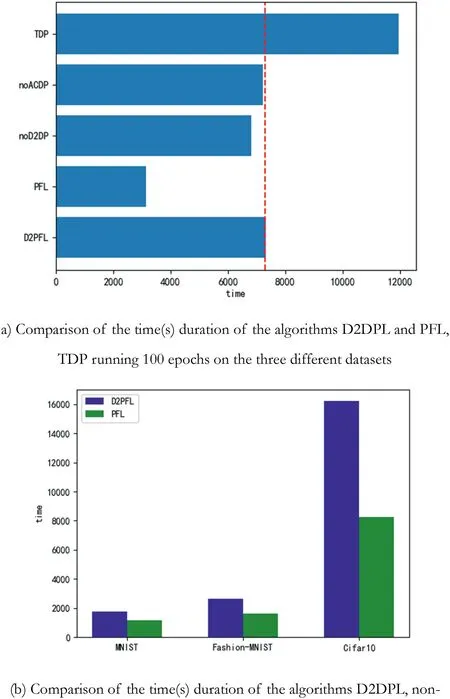
F I G U R E 4 Comparison of the time(s) consumed

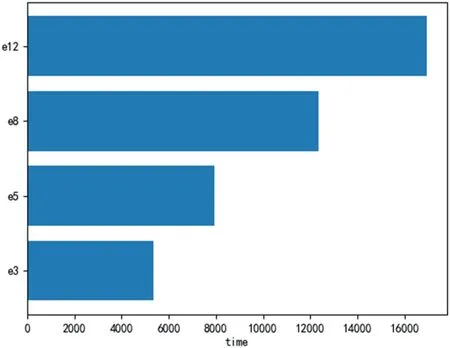
F I G U R E 5 The time(s)consumed for training 20 epochs when ∊total set to 3, 5, 8, and 12, respectively, are compared on the Fashion-MNIST dataset

6 | SUMMARY

F I G U R E 6 Comparing the accuracy of the test on the Fashion-MNIST dataset using different ∊total set to 3, 5, 8, 12, respectively,corresponding to training the data at different levels of noise amount

The paper first attempted to apply the improved dynamic differential privacy to neural network-based federated Learning models.Specifically, a new differential privacy federation learning model (D2PFL) was proposed, which relies on differential privacy to build a federation learning model for deep neural networks.Such models can be used to generate and share data models with provable privacy.Then, the performance of the model was evaluated on real datasets,and the results show that the approach provides an accurate representation of large datasets with strong privacy guarantees and high practicality.As part of future work, we plan to provide different privacy guarantees for various types of different client,and to adapt to the big data environment and generate models more efficiently in more complex data contexts by improving the communication efficiency of the federated learning model and improving the differential privacy aggregation.

ACKNOWLEDGEMENTS

This work was supported by the National Natural Science Foundation of China under Grant No.62062020 and No.72161005, NO.62002081, NO.62062017, Technology Foundation of Guizhou Province (grant no.QianKeHeJiChu-ZK[2022]-General184), and Guizhou Provincial Science and Technology Projects[2020]1Y265.

DATA AVAILABILITY STATEMENT

Data that support the findings of this study are available from the corresponding author upon reasonable request.

ORCID

Shengnan Guohttps://orcid.org/0000-0002-7131-5814

APPENDIX

that is, post-unionσc≈4.92<σt≈5.73

It can be seen that assumingH0holds, the privacy budget increases with each round of iteration while being independently identically distributed.

The proof of the theorem 4 relies on the following moments bound on Gaussian mechanism with random sampling.