平行钢绞线斜拉索无应力索长求首股力的方法

朱斌，韩志星，邵文达

（江西省交通运输科学研究院有限公司，江西 南昌 330200）

1 等值张拉法

等值张拉法一般按以下原则进行现场实施：

第1、2 根：为减少HDPE 外套管对单根张拉力造成过大的非线性影响，第1、2 根钢绞线用来承受HDPE外管的自重，拉索单位一般会根据施工经验先预估一个大概的单根张拉索力值（比如：14～15 吨）；待整束拉索最后一个孔位钢绞线安装完毕，将第1、2 根钢绞线放张然后重新张拉；

第3 根：根据整束拉索索力平均之后由主梁及索塔的变形量进行修正，使安装完成之后单根索力累计值与设计接近，避免单根挂索之后索力大调整。索力大小按下式确定：

式中：T3—第3 根钢绞线控制力；N12—第1、2 根钢绞线控制力；n—斜拉索孔数；—斜拉索安装时锚点相对变形理论值；l—斜拉索索长；Ec—钢绞线弹模；A—钢绞线截面面积。

由此在确定首股力后的前提下,即可求得剩下钢绞线的张拉力值。

目前采用的等值张拉法关键是确定首股钢绞线的张拉力，本文采用无应力索长确定首股力旨在通过斜拉索张拉工况无应力索长的不变性来较为精确的给出首股力值，避免张拉完后索力再进行不必要的调整，在首根或者前m 根的第m 根钢绞线上安装传感器来确保各钢绞线的索力均匀性。

2 无应力索长悬链线理论

目前普遍采用考虑垂度效应的悬链线理论来计算无应力索长。拉索整体受力示意图和拉索微单元图如图1～2 所示。

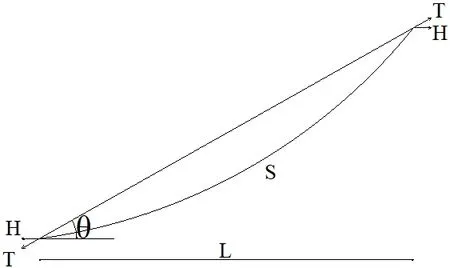
图1 拉索整体受力示意图

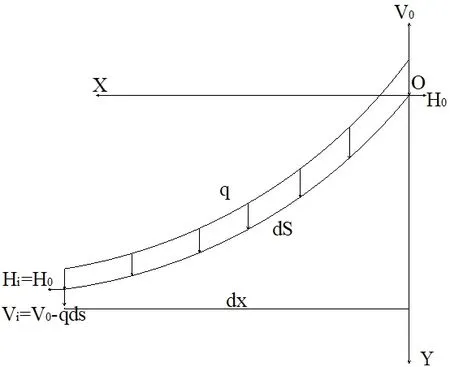
图2 拉索微单元图

悬链线理论基本假定：（1）斜拉索为只受拉的理想柔性索，不考虑其弯曲刚度；（2）斜拉索材料符合虎克定律；（3）斜拉索材料集重沿索长均匀分布；（4）斜拉索符合平截面假定。

式中：ds 为拉索微单元长；H=H0为索水平分力，受拉为正；V 为索竖向分力，以绕O 点顺时针旋转为正；q 为索的自重集度。

3 无应力索长反算首股力

（1）已知梁上锚点坐标为（X0，Y0，Z0）,塔上锚点坐标为（X1、Y1、Z1）。拉索张拉后梁上锚点坐标变形量；塔上锚点坐标变形量为最终态求出拉索的无应力索长S0。

（2）通过第一步求得的S0，反代入（12）式中因只有一个未知量H，可求出H，从而可求出首股索力T1。通过在首股钢绞线，也可以多穿几根钢绞线（设为m 钢绞线）作为起始，前m 根钢绞线索力应均匀，在第m 根钢绞线上安装索力传感器，后续m+1～n 号钢绞线张拉至和第m 根钢绞线等值即可确保索力均匀性及无应力索长的一致性。

4 工程实例

广西平南相思洲大桥为40+170+450+170+40 m 分离式双箱组合梁斜拉桥。斜拉索采用空间双索面扇形布置，主塔两侧各分别布置20 对索，全桥共80 对索。斜拉索采用抗拉强度为1860MPa 的预应力钢绞线斜拉索，疲劳应力幅不小于200MPa。根据索力不同，采用15.2-37、15.2-43、15.2-55、15.2-61、15.2-73、15.2-85 共6 种规格。斜拉索在塔上均采用钢锚梁锚固，在梁上采用锚拉板进行锚固。

拉索编号为A20～B20，A20 为边跨最长索，A1 为边跨最短索，B1 为中跨最短索，B20 为中跨最长索。以A2 号索为例，先通过上述无应力索长悬链线理论公式（12）求解张拉后工况的无应力索长S0，如表1 所示（注：表1 中梁端及塔端锚点坐标为拉索张拉后的对应的坐标值）。

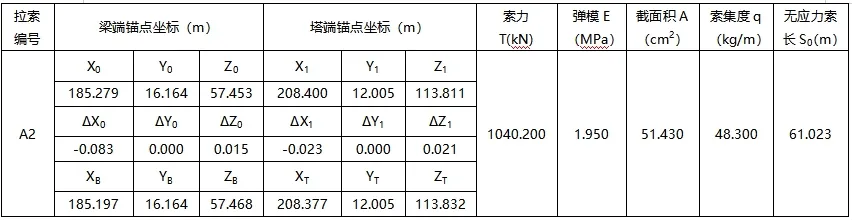
表1 相思洲大桥北塔A2 拉索无应力索长计算结果

在表1 求得的无应力索长S0的基础上，反代入公式（12）逆向求出钢绞线首股力，如表2 所示（注：表2 中梁端及塔端锚点坐标为拉索张拉前对应的坐标值）。

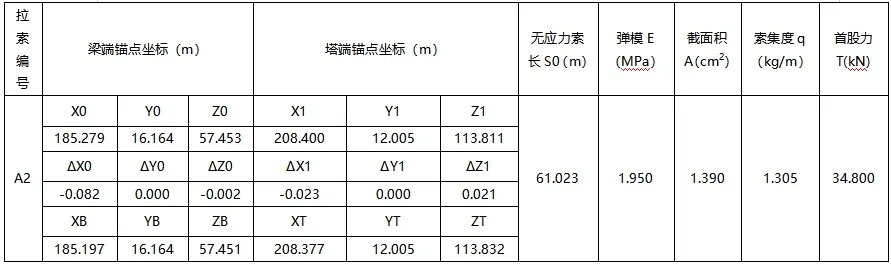
表2 相思洲大桥北塔A2 拉索钢绞线首股力计算结果

根据上述方法求得的首股力，再通过等值张拉法（详见第1 节）张拉后的索力和监控指令张拉索力进行对比，结果如表3 所示。从表中可以看出各典型索（短索、中索、长索取数根）最终张拉索力值和监控指令值百分比误差最大1.069%，此误差值满足工程应用要求。

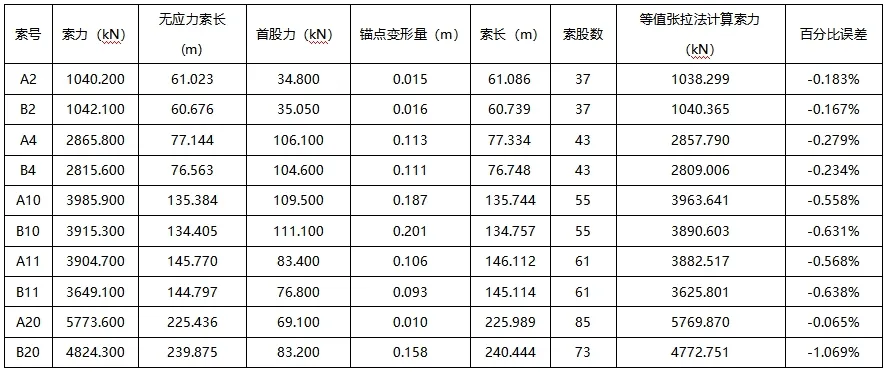
表3 相思洲大桥北塔典型拉索无应力索长反算首股力后等值张拉结果和监控指令值对比

5 结语

等值张拉法是目前钢绞线索张拉采用的普遍方法，本文通过无应力索长在张拉工况的不变性，先求得张拉后拉索的无应力索长S0，再通过第一步求得的无应力索长S0，反代入公式（12）逆向求出首股钢绞线索力，进而结合等值张拉法，使得最终张拉索力达到预期值（监控指令值），本文典型拉索张拉后误差百分比误差最大为1.069%，满足规范和工程应用要求。

本文未考虑温度变化等对结构影响，后续研究可在考虑温度变化等影响因素的基础上进一步优化计算方法。