非平稳性条件下设计洪水地区组成分析

胡义明,杨晨曦,梁忠民,唐 超,陈 钰,郭举坤

(河海大学水文水资源学院,江苏 南京 210098)

在分析工程对下游的防洪作用以及进行水库群联合调洪计算时,需要解决设计洪水的地区组成问题,以厘清当设计断面发生指定标准设计洪水时,上游水库及其区间的洪水空间组成情况。设计洪水地区组成的计算方法主要有地区组成法、频率组合法和随机模拟法[1]。在实践应用中,地区组成法中的同频率组合法最为常用,即根据工程防洪要求,指定某一局部地区的洪量与下游控制断面的洪量同为设计频率,再根据水量平衡原则推求其余分区的洪量,如典型的“上游和下游同频、区间相应”或“下游和区间同频、上游相应”方法[2-3]。设计洪水地区组成分析是一种多维洪水特征变量联合求解问题,诸多研究也采用Copula函数构建不同区域洪水特征变量间的联合分布函数,以此推求设计洪水的地区组成[4-6]。应用上述各类方法分析设计洪水地区组成时,都需要洪水样本系列满足平稳性要求。然而,由于气候变化和人类活动的影响,诸多站点的洪水样本系列呈现非平稳性变化,理论上,现行的基于平稳性假定的工程水文计算理论与方法已不再适用于变化环境下的非平稳性情形,给设计洪水地区组成分析带来了挑战[7-11]。目前,变化环境下水文设计值的计算主要有3种途径:①基于水文极值系列重构途径;②基于分布函数加权综合途径;③基于变参数概率分布模型途径[9]。诸多研究主要集中在单一洪水变量设计值计算或不同时段洪量组合设计值计算方面[12-16]。关于非平稳性条件下,如何分析设计洪水的地区组成的研究较少,是工程水文领域亟须解决的难题。

本文基于Copula函数构建不同区域非平稳性洪量系列间的变参数多维联合分布模型,结合条件期望组合法和等可靠度法,研究非平稳性条件的设计洪水地区组成计算问题,并以寸滩站和宜昌站年最大15d洪量为例进行了应用分析。

1 理论与方法

1.1 非平稳性边缘分布模型

以我国设计洪水计算规范中推荐的皮尔逊三型分布(PE3)为基础,假定PE3分布中的某些参数随其他因素(协变量)变化,构建非平稳性边缘分布模型,以描述洪水特征的非平稳性分布规律。非平稳性PE3密度函数为[14]

(1)

其中αt=AZ+a0βt=BH+b0γt=CW+c0

式中:x为洪水特征变量;αt、βt、γt分别为PE3分布中t时刻的位置参数、尺度参数和形状参数;Γ(γt)为Gamma函数;Z、H、W分别为影响位置参数、尺度参数和形状参数变化的环境状态变量因子集;A、B、C、a0、b0、c0为系数。

1.2 非平稳性多维联合分布模型

考虑到不同洪量自身的非平稳性及其相依结构的非平稳性,基于Copula函数构建可综合分析上述两类非平稳性的变参数Copula模型[14],用于描述不同年份多变量联合分布规律的演变特征。在变参数Copula模型中,各变量边缘分布参数及Copula结构参数随协变量变化,不再是常数[14-17]。

本文以常用的Gumbel Copula函数为基础,构建非平稳性多维联合分布模型,以分析非平稳性条件下不同区域洪水特征变量联合分布特征随时间的演变规律。非平稳性Gumbel Copula函数可表示为[14,18]:

C(μt,νt)=exp{-[(-lnμt)θct+(-lnvt)θct]1/θct} (θct≥1)

(2)

其中θct=exp(θD+θ0)+1

式中:C(·)为时变Gumbel Copula函数;μt、vt为第t年变量xt和yt对应的概率值;θct为第t年Gumbel Copula模型的结构参数;D为影响参数θct变化的协变量;θ和θ0为系数和截距。

1.3 条件期望组合法

基于构建的不同区域间洪量(如上、下断面洪量间或下断面与区间洪量间)的非平稳性Gumbel Copula函数,可以推求给定下断面设计洪量X=xp(xp为超过频率p对应的下断面设计流量)条件下,上断面洪量或区间洪量Y的条件概率密度函数。基于该条件概率密度函数,可进一步推求xp对应的Y的条件期望值yt,E。(xp,yt,E)即为变量X和变量Y的条件期望组合[14]。

1.4 等可靠度法

等可靠度方法是由梁忠民等[19]提出,可用于推求非平稳性条件下指定重现期的洪水设计值。以RS、RNS分别表示一致性、非一致性条件下,工程设计年限L和设计重现期T对应的水文设计可靠度,其计算公式为

(3)

式中:Ft(XT,NS)为第t年水文极值的概率分布函数;XT,NS为指定重现期T对应的下断面洪量设计值。

根据等可靠度方法:令RNS=RS,即可获得非平稳性条件下的XT,NS。通过变量X和变量Y的条件期望组合(xp,yt,E),可计算XT,NS条件下Y对应的条件期望值yT,E、XT,NS和yT,E的差值为区间(或上断面)的洪量;进而获得指定设计标准条件下,上、下断面及区间的设计洪量组合。

1.5 模型评价

采用赤池信息量准则(AIC)和贝叶斯信息准则(BIC)对模型进行评价。AIC和BIC是评估模型性能的常用指标[20]。AIC建立在熵的概念基础上,可以权衡所估计模型的复杂度和此模型拟合数据的优良性 。模型参数个数越少,模型越简单,AIC值越小;对数似然值越大,模型精度越高,AIC值也越小。因此AIC准则对模型的评价兼顾了模型的简洁性和精确性。AIC值越小,模型越好。

BIC准则是对AIC准则的改进,其将未知参数个数的惩罚权重由AIC准则中的常数2变成了样本容量。BIC值越小,模型越优。

2 实例分析

以长江流域寸滩站和宜昌站1946—2014年的年最大15d洪量系列为例进行实例分析。寸滩站位于长江干流上游,是三峡水库入库重要控制站,集水面积约86.66万km2,宜昌站位于长江干流中游,集水面积约100.55万km2(图1)。

图1 宜昌站和寸滩站位置信息

由图2可知,寸滩站、宜昌站的洪量系列均存在下降趋势。Mann-Kendall统计量的计算值分别为-2.6261和-3.319,其绝对值均大于0.05显著性水平下对应的阈值1.96,表明两站年最大15d洪量系列减少趋势显著。

图2 寸滩站、宜昌站年最大15d洪量系列

为了描述寸滩站和宜昌站年最大15d洪量的非平稳性分布特征,采用了非平稳性PE3分布模型。在模型构建中,考虑到PE3分布函数中的参数必须大于0这一约束,参数均采用指数回归形式。通过设定PE3分布函数中的位置参数和尺度参数随时间变化,构造了2种形式的非平稳性PE3模型:分布函数中位置参数随时间变化(PE3(L))、分布函数的位置参数和尺度参数随时间变化(PE3(LS))(表1)。

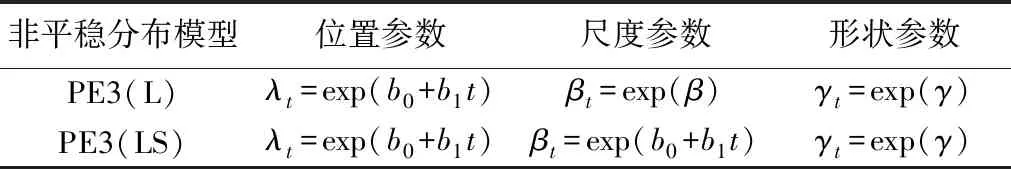
表1 时变边缘概率分布模型

关于非平稳性边际分布函数和变参数Copula模型中的参数估计,均采用贝叶斯方法并结合马尔科夫链蒙特卡洛方法(MCMC)抽样技术进行估计,以最大后验估计作为模型使用参数[12,16-17]。在抽样过程中,平行运行5条链,每条链上抽取30000个样本(每条链都能满足收敛要求),去掉预热的29000个样本,每条链上仅采用最后的1000个样本,5条链共计5000个样本,其中使参数后验密度值达到最大的为参数的最大后验估计。

由表2可知,PE3(L)模型在寸滩站表现最优;而对于宜昌站,PE3(L)和PE3(LS)模型对应的AIC和BIC值较为接近,但考虑到PE3(LS)模型具有更大的不确定性,最终选取PE3(L)模型描述宜昌站年最大15d洪量的非平稳性分布特征[13]。表3给出了优选的非平稳性边际分布函数和变参数Copula函数中的参数估计值。

表2 非平稳性分布模型对应的AIC和BIC值

基于非平稳性Gumbel Copula函数模型分析了寸滩站和宜昌站年最大15d洪量系列的联合分布随时间的演变特征。图3(a)给出了1990年、2000年、2010年、2020年和2030年5个典型年不同联合概率(0.4、0.6、0.8、0.95)条件下,两站年最大15d洪量联合分布规律的演变特征。由图3(a)可知,对于指定的联合概率,5个典型年份的联合分布是不同的,这就导致2个站点年最大15d洪量的最可能组合在不同年份不同。

图3 寸滩站和宜昌站年最大15d洪量联合分布特征

图3(b)给出了1990年、2000年、2010年和2030年4个典型年不同联合重现期(10a、20a、50a、100a)条件下,宜昌站和寸滩站年最大15d洪量联合分布特征变化特征。由图3(b)可知,对于给定的联合重现期,2个站点年最大15d洪量的最可能组合在不同年份不同。

基于非平稳性分布模型PE3(L),计算了0.01和0.02超过概率对应的宜昌站年最大15d洪量的分位数(2015—2114年)。结合非平稳性Copula模型,计算了不同超过概率条件下,与宜昌站年最大15d洪量对应的寸滩站年最大15d洪量的条件期望值,进而获得了不同概率条件下宜昌站和寸滩站年最大15d洪量的组合样本系列。基于该组合样本系列,构建了不同超过概率条件下两站年最大15d洪量之间的条件期望组合关系曲线,如图4所示。

图4 不同超过概率条件下寸滩站和宜昌站年最大15d洪量的期望组合关系

根据等可靠度方法计算了不同重现期(50a和100a)条件下,不同工程设计寿命(10～100a)对应的宜昌站年最大15d洪量的设计值。随后基于不同超过概率下宜昌站和寸滩站年最大15d洪量的条件期望组合关系曲线,推求了不同重现期条件下,与宜昌站年最大15d洪量设计值对应的寸滩站年最大15d洪量设计值。由于宜昌站的来水与寸滩站来水及区间来水要满足水量平衡约束,为此宜昌站和寸滩站设计值之差即为区间来水设计值,结果如图5所示。

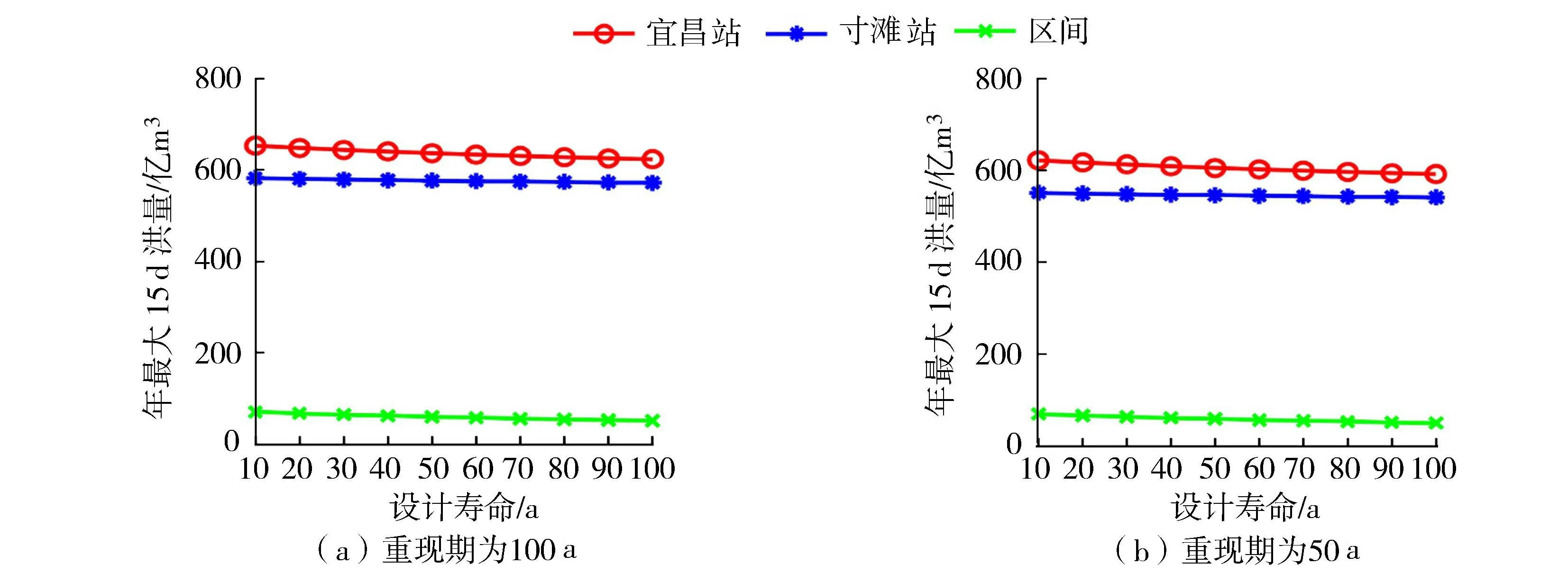
图5 不同重现期条件下宜昌站、寸滩站及区间的年最大15d洪量设计值

由图5可知,在同一重现期条件下,宜昌站和寸滩站的洪量设计值随着设计寿命的增加呈现减少趋势,这主要是由两站的洪量系列本身呈现减少趋势导致。如在宜昌站设计重现期为100a、工程设计寿命为10a和50a条件下,宜昌站、寸滩站及相应区间洪量的设计值分别为(652.8,581.9,70.9)和(636.5,576.4,60.1)。在指定重现期条件下,宜昌站、寸滩站及区间的年最大15d洪量设计值随着工程设计寿命增加而减小。

3 结 语

本文构建了可综合考虑不同区域洪量边缘分布非平稳性及区域洪量间相关结构非平稳性的时变动态Copula模型,可用于分析不同区域洪水间的多维联合分布规律随时间的非平稳性演变特征。综合运用等可靠度法和条件期望组合法,提出了变化环境下设计洪水地区组成分析方法,可用于变化环境下指定重现期对应不同区域洪水组合设计值的推求。宜昌站和寸滩站的应用结果表明,宜昌站、寸滩站及两站区间洪水设计值均随着工程使用年限的增加呈减小趋势,这与宜昌站、寸滩站的洪量系列本身的减少趋势相吻合。

在示例分析中,关于非平稳性Copula模型的构建,限于资料条件,只考虑了边缘分布参数和Copula结构参数随时间因子变化,而没有考虑其他因素对模型参数的影响。在后续研究中,可考虑基于不同类型Copula函数、不同因素驱动模型参数变化等方式,构建多套不同的非平稳性Copula模型,并通过优选方式确定优势联合分布模型。