不同箔坝位置关系下浮动坝箔片端面气膜密封性能研究

陈 源, 熊 聪, 彭旭东, 李运堂, 李孝禄, 王冰清, 金 杰*

(1.中国计量大学 机电工程学院, 浙江 杭州 310018;2.中国计量大学 浙江省智能制造质量大数据溯源与应用重点实验室, 浙江 杭州 310018;3.浙江工业大学 机械工程学院, 浙江 杭州 310032)

目前干气密封被广泛应用于中高速旋转机械的轴端密封[1-2]，当旋转机械工况稳定时，干气密封运行稳定性较好[3-5]，但当轴系发生剧烈振动或工况发生明显扰变时，干气密封易因端面碰磨和撞碎等情况引发失效[6-7].随着现代工业的快速发展，旋转机械也将向更高参数工况发展，这对干气密封的抗振性和可靠性提出了更严格的要求[8-9]，尤其在石油石化、能源电力和航空航天等领域，密封失效不仅会造成巨大经济损失，还有可能引起重大安全事故.

传统干气密封其密封环多为脆性实体结构[10]，碰撞易碎，且散热性较差，难以适应超高速、高温和高振动等极端工况.为解决上述问题，Heshmat[11]、Agrawal[12]等借鉴弹性箔片气体推力轴承在高参数工况下的成功应用经验，设计出由底层波箔片支撑顶层平箔片的弹性箔片端面气膜密封(Compliant foil face gas seal，简称CFFGS).随后，Munson等[13]对CFFGS开展实验研究，结果表明CFFGS在中高压工况下具有优越的控漏性能，并且弹性端面自适应变形能有效减小轴系振动带来的不利影响.Salehi等[14]将CFFGS用于航空发动机模拟器并对其运行过程进行实时监测，结果发现CFFGS在极端工况下有良好的表现.Heshmat等[15]进一步在不同压力与转速下对CFFGS进行试验，同样证实了CFFGS具有优异的密封性能.上述试验研究均表明，CFFGS在高速、高温和高振动等极端服役环境下表现出较好的应用效果，因此对其深入开展理论研究，以期掌握CFFGS运行机理和设计方法并进一步实现推广应用，具有重要的工程价值和战略意义.

目前关于CFFGS的理论研究较少，而箔片轴承因研究历史较长，相关理论体系更为成熟，由于两者之间结构和原理的相似性，箔片轴承理论体系可为CFFGS研究提供重要参考.Walowit等[16]早在1975年就提出了箔片刚度的计算公式，随后Heshmat等[17]利用该公式建立了经典的箔片结构等效弹性基础模型，从而开启了弹性箔片动压气体轴承的研究热潮，相关研究涉及气体箔片轴承的承载特性或稳定性研究[18-22]、动态性能研究[23-27]以及热力特性研究[28-31]等.上述研究均要以建立计算膜压与箔片变形的气弹耦合润滑模型为基础，这也同样是对CFFGS开展研究的重要前提.近年来，本文作者所在研究团队参考箔片轴承理论体系，对CFFGS进行理论建模与求解，并系统开展稳、动态性能研究[32-34].结果表明，高速CFFGS不仅具有良好的综合密封性能，同时依靠柔性端面的自适应变形协调作用，在膜厚大幅扰变下也具有优异的动态稳定运行能力.徐洁等[35]同样对柔性端面气膜密封开展理论研究，结果表明，相较于刚性端面气膜密封，柔性端面气膜密封在高速低压的工况下具有更稳定的综合密封性能.

为保证密封性，现有CFFGS研究中设有密封坝，而刚性密封坝结构会一定程度上影响密封自适应运行能力，同时也会存在碰撞碎裂风险，为进一步解决上述问题，在箔片气体推力轴承和现有CFFGS结构基础上，本文中提出一种具有浮动密封坝的箔片端面气膜密封(Floating seal dam compliant foil face gas seal，简称FSD-CFFGS)结构，即在密封坝底部设计柔性箔片支撑，并以其为研究对象建立气弹耦合理论模型，在不同箔坝初始位置关系下系统研究箔片区支撑箔柔度系数α1和浮动坝区支撑箔柔度系数α2对密封性能的影响，揭示密封运行机理，给出α1和α2的优选范围，为FSD-CFFGS性能评估与工程设计提供一定理论指导.

1 理论模型

1.1 物理模型

图1所示为FSD-CFFGS密封环模型示意图，该结构包含箔片区、浮动坝区与底座三部分.箔片区包括弹性平箔片和弹性波箔片，浮动坝区包括密封坝、弹性波箔片和辅助密封圈，需要说明的是，在密封坝底部设置柔性支撑，不仅能在膜厚和工况扰变时通过自适应浮动达到改善密封性能的目的，还可以提升密封坝的抗冲击能力.此外，由弹性波箔片支撑形成的底部镂空结构有利于散热，可有效避免温度过高引起的密封环热裂问题.

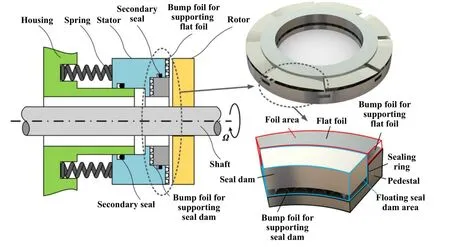
Fig.1 Model schematics of FSD-CFFGS图1 FSD-CFFGS模型示意图

如图2所示，左侧为FSD-CFFGS箔片区单周期周向膜压分布示意图，右侧为浮动坝区单周期周向膜压分布示意图，图3所示为FSD-CFFGS径向膜压分布示意图.图2所绘的箔片区支撑波箔片与浮动坝区支撑波箔片在数值计算中近似等效为图3所绘等效弹簧[36].

Fig.2 Circumferential pressure distribution schematics of FSD-CFFGS single cycle图2 FSD-CFFGS单周期周向膜压分布示意图

Fig.3 Radial pressure distribution schematics of FSD-CFFGS图3 FSD-CFFGS径向膜压分布示意图

图4(a)、(b)和(c)所示分别为初始状态(未发生变形)下箔片端面位置高于、等于和低于密封坝平面位置的结构示意图，以Δh表征未发生变形时箔片端面与密封坝平面的初始高度差，对应设定初始状态下箔片高于密封坝平面时，Δh>0；箔片与密封坝平面齐平时，Δh=0；箔片低于密封坝平面时，Δh<0.

Fig.4 Three types of foil-dam positions structural schematics for FSD-CFFGS in initial state图4 初始状态下FSD-CFFGS三种箔坝位置结构示意图

1.2 数学模型

假设FSD-CFFGS密封端面间为等温、层流流体[37]，则计算密封端面膜压的可压缩雷诺方程[38]为

其中，p为端面气膜压力；μ为气体黏度；ω为角速度；h为端面气膜厚度；θ为圆周坐标；r为半径坐标.

图5所示为FSD-CFFGS端面膜厚分布示意图，表达式如下：

Fig.5 Schematics of gas film thickness图5 气膜厚度示意图

其中，hd(r,θ)为浮动坝区膜厚分布，hf(r,θ)为箔片区膜厚分布，其表达式分别如式(3)和(4)：

其中，h0为箔片密封环未受力变形的初始状态下密封坝平面到配副密封端面的距离，hs(r,θ)为FSD-CFFGS端面形变量，其计算表达式如式(5)所示：

其中，α1为箔片区支撑箔柔度系数，α2为浮动坝区支撑箔柔度系数，支撑箔柔度系数反映箔片受力变形的能力且支撑箔柔度系数越大，箔片受力越易变形，p1为密封环外径侧边界压力.

式(4)中的hw(r,θ)则为初始状态下平箔片斜坡区上任意点到平箔片水平区所在平面的距离，其计算表达式如

其中，β为单周期箔片区所占角度；b为节距比，是斜坡区占箔片区的比例；h1为楔形高度.

根据FSD-CFFGS结构和环境特征，求解方程(1)所采用的边界条件为

(1)不同径向位置压力边界条件为

其中，p0为密封环内径侧边界压力.

(2)周期性压力边界条件为

端面开启力F与轴向气膜刚度K的计算表达式分别如式(9)和式(10)：

密封泄漏率计算表达式为

用以表征密封综合性能的刚漏比采用式(12)计算：

2 结果与讨论

数值计算所采用的基本结构和工况参数列于表1中.

表1 初始参数数值表Table 1 Initial parameters

2.1 计算流程与对比验证

本文中计算流程如图6所示，首先使用有限差分法离散稳态雷诺方程，通过数值计算方法迭代求解收敛膜压、箔片变形及膜厚分布.图中m和n分别为周向和径向网格数.膜压收敛残差为1×10−5，膜厚收敛残差为1×10−7.

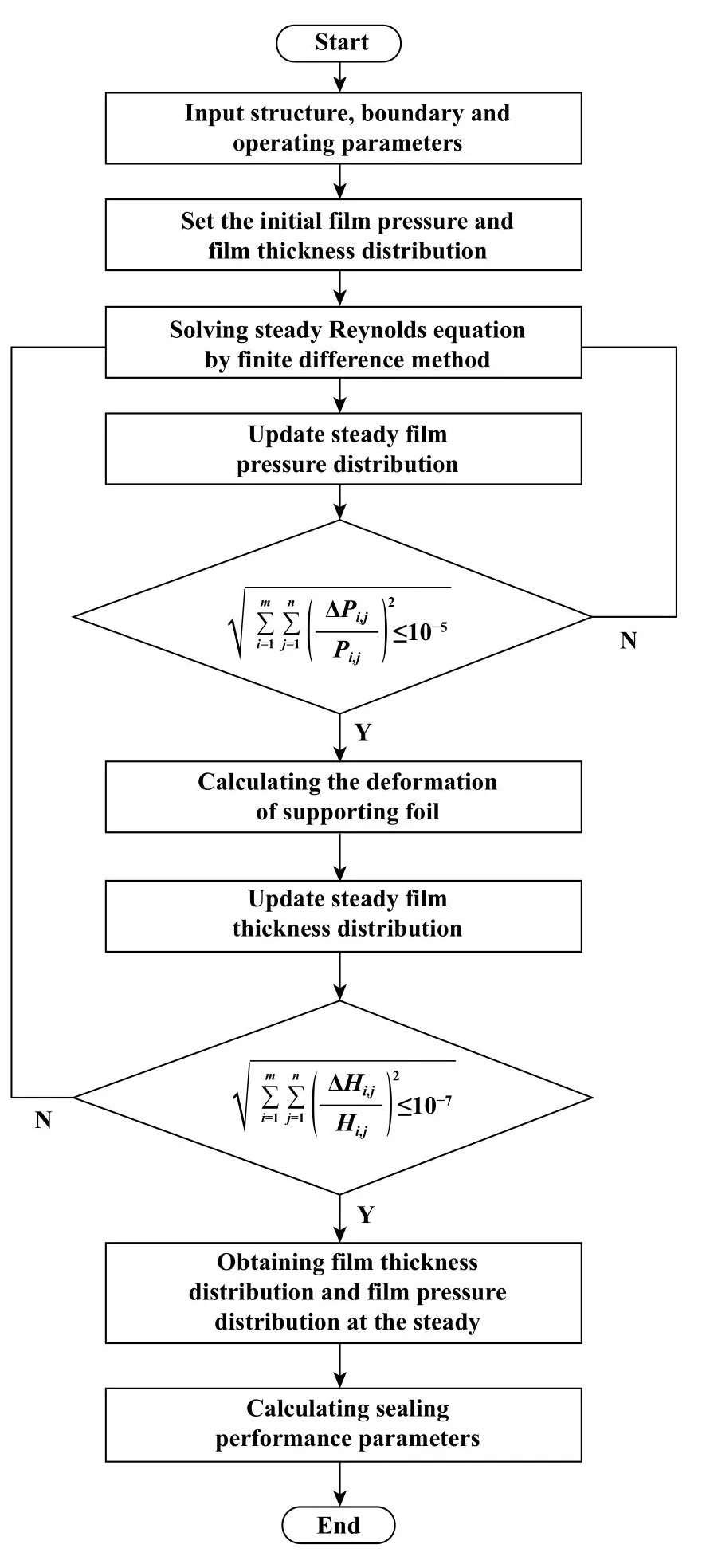
Fig.6 Calculation flow chart图6 计算流程图

由于FSD-CFFGS与箔片气体推力轴承润滑理论模型基本一致，因此与箔片气体推力轴承相关文献[36, 39]进行对比验证，从图7可以看出，结果吻合较好，从而验证了本文程序的正确性.

Fig.7 Comparison and verification图7 对比验证

2.2 箔坝位置的影响分析

图8所示为三种初始箔坝位置关系下的端面膜压分布图，由于箔片斜坡区与配副端面构成楔形间隙，当密封环高速旋转时，在气体动压效应的作用下，箔片端面会产生明显高压区，最高压力发生在箔片斜坡区与水平区交界处.需要说明的是，由于箔片底部为镂空结构，箔片外径侧高压流体亦可通过镂空通道流至箔片四周，因此箔片四周边界压力均与流体介质压力相等.对比图8(a)、(b)和(c)可以发现，箔片相对密封坝位置越高，气膜高压区的范围越大，密封开启性能越好.上述现象主要是因为箔片位置较高时，箔片区气膜间隙较小且在合适范围内，此时流体的动压效应作用较强.

Fig.8 Gas film pressure distribution of FSD-CFFGS under three types of initial foil-dam positions图8 三种初始箔坝位置关系下FSD-CFFGS端面膜压分布图

图9所示为三种初始箔坝位置关系下密封端面形变及浮动量分布图，从图9中可以看出，在膜压作用下，箔片区将发生变形，且在不同箔坝位置关系下，箔片因受不同气膜压力作用而发生相适应的变形，以达到自适应协调的效果.同时，密封坝位置也将进行一定量的自适应浮动，由于密封坝上作用的气膜压力不受箔片区上力的影响，因此当密封坝上膜压分布不变时，其浮动量也均会保持不变.

Fig.9 Deformation and floating quantity distribution of FSD-CFFGS under three types of initial foil-dam positions图9 三种初始箔坝位置关系下FSD-CFFGS端面形变及浮动量分布图

2.3 支撑箔柔度系数的影响分析

图10(a)、(b)和(c)分别示出了三种初始箔坝位置关系下箔片区支撑箔柔度系数α1对密封端面上M1、M2和M3三点膜压p和形变量u的影响曲线.其中M1为箔片斜坡区中心点，M2为箔片斜坡区与水平区交线的中点，M3为箔片水平区的中心点.随着α1的增大，三点处的p均呈现递减趋势，相应u呈现递增趋势，这表明α1较大时，其自适应性较好，但形变量的增大导致动压效应减弱从而降低密封开启性能，因此在设计α1时要综合考虑自适应性与开启性.此外，当高度差Δh较大时，p和u也相应较大，这进一步说明Δh较大时有利于动压效应的增强.图10(d)所示为三种初始箔坝位置关系下浮动坝区支撑箔柔度系数α2对密封坝中心点N膜压p和浮动量u的影响曲线.可以看出，随着α2的增大，u呈现增大趋势，p则略微减小，这是因为α2增大表示浮动坝区支撑箔受力更容易发生变形，由于密封坝外径到内径的压力均呈线性分布，且内、外径边界压力并未发生变化，故N点的膜压变化幅度较小.上述研究表明α2的变化对浮动坝区的开启力影响甚微，但膜厚变化会影响控漏性，故设计α2时应重点考虑自适应性和控漏性.

Fig.10 Influence of supporting foil compliance coefficient on gas film pressure and deformation (floating quantity)图10 支撑箔柔度系数对密封端面膜压与形变量(浮动量)的影响规律

2.4 高度差的影响分析

为进一步研究高度差Δh渐变所带来的影响，图11和图12所示分别为Δh对密封端面上M1、M2、M3和N四点的膜压p、形变量(浮动量)u以及开启力F、气膜刚度K、泄漏率Q和刚漏比Γ等密封性能参数的影响规律.从图11可以看出，随着Δh的增大，箔片区各点均呈现增长趋势，M2和M3点膜压和形变量受Δh影响较大，当Δh大于−2.0 μm时，M3点膜压和形变量超过M1点，这也间接说明Δh较大时主要是通过影响箔片水平区来起作用.同时，可以看出Δh对浮动坝区的N点始终未有影响，这也进一步验证了上文中关于箔坝位置关系对浮动坝区无影响的推测.从图12可以看出，由于Q主要取决于密封坝位置及压力差，故不受Δh影响.而F、K和Γ则随Δh增大呈现增速递增的变化趋势，因此在做FSD-CFFGS结构设计时，应在膜厚设计允许范围内尽量增大Δh.

Fig.11 Influence of Δh on gas film pressure and deformation (floating quantity)图11 Δh对密封端面膜压与形变量(浮动量)的影响规律

Fig.12 Influence of Δh on sealing performance parameters图12 Δh对密封性能参数的影响规律

2.5 三种箔坝位置关系下支撑箔柔度系数对密封性能的交互影响分析

图13所示为三种初始箔坝位置关系下箔片区支撑箔柔度系数α1和浮动坝区支撑箔柔度系数α2对密封性能参数的交互影响云图.从图13(a)和(b)可以看出，α1和α2对开启力F和气膜刚度K均有一定影响，且不同初始箔坝位置关系下，α1和α2对F和K的影响作用不同，当高度差Δh小于0 μm时，α1和α2对F和K影响作用相当，而Δh大于0 μm时，α1的影响作用更为显著.由图13(c)可知，泄漏率Q只受α2的影响，原因是α2改变，密封坝浮动量也随之变化，导致浮动坝区膜厚发生改变从而影响泄漏率.从图13(d)可知，通过合理配置α1和α2可获得较好的综合密封性能，考虑Δh的影响并保障一定程度的自适应变形能力，当α1取0.05~0.15、α2取10−5~10−3时，密封具有较好的综合性能.

Fig.13 Influence of supporting foil compliance coefficient on sealing performance parameters图13 支撑箔柔度系数对密封性能的影响规律

3 结论

a.FSD-CFFGS可通过膜压、膜厚和箔片形变与密封坝浮动之间的相互协调作用，使密封趋于稳定并具有良好的自适应能力.

b.Δh越大，所产生的动压效应越强，开启性越好，故在开展FSD-CFFGS结构设计时，应在平衡膜厚设计范围内尽量增大Δh.

c.通过合理配置α1和α2可有效提升密封综合性能，当α1取0.05~0.15、α2取10−5~10−3时，FSD-CFFGS兼具一定自适应变形能力的同时也具有较好的开启性和控漏性.