小学数学校本作业中题组设计的实践策略

蔡洪龙

题组作业指的是教师根据教学实际与学生的现实学情，将有关联的、零散的习题综合重组，实现新旧知识的勾连、对比与巩固。题组作业促使习题设计从“重复低质”走向“增效高质”，有效地让学生从“题海战术”中跳出，达到“少”而“精”、融会贯通的练习效果。题组作业的设计重在比较，不同于单一的练习，在突出数学知识重点、突破难点、厘清知识易混点等方面有着显著作用。教师要明确题组习题设计并非简单数学问题的组合，而是要让题组作业具有层次性、联系性、变式性和开放性等，有效地发展学生的分析、应用、迁移和创造等高阶思维。

正因为题组习题有其独特的现实价值，使得它在校本作业中占有重要地位。为此，教师应灵活地根据数学知识重难点、易混点、规律点而巧妙设计题组习题，以最少、最优的题量实现最大、最佳的育人效益，发展学生的数学思维，助推“双减”落地。

一、设计层次性的题组作业，让学生思维拾级而上

学生之间存在着个体差异，在设计校本作业中的题组习题时，教师要兼顾不同层次学生的学习水平，给潜能生一个台阶，让他们能根据自己的学习水平而拾级而上，让不同的学生能通过题组练习而得到不同层次的发展。为此，题组设计要由浅入深、由易到难，让不同水平的学生都能在适合自己的习题中得到相应的启发与提升，促使每一位学生的思维都能在当下量级上得到提升和发展。例如，在教学人教版数学教材三年级下册“长方形、正方形的面积计算”这一内容之后，笔者设计了这样的题组：

1. 一块空地，长16 m，宽8 m，求这块地面积是多少？

2. 一块空地，长16 m，宽8 m，大伯准备在这块空地上每4 m2栽一棵树，总共能栽多少棵树？

3. 一块空地，大伯准备在长不变的基础上，把它的宽增加2 m，面积就增加32 m2；如果他要把这块空地的长增加6 m，而宽不变，面积就会增加48 m2，求这块空地原来的面积是多少？

这样具有层次性的题组作业设计，能充分兼顾不同水平的学生，第1 题属于基础性的习题，学生只需照搬所学的长方形面积的计算公式就可以解决问题，属于一种模仿性质的低阶思维，适合潜能生的基础练习；而第2 题则是属于巩固性练习，要求在会运用公式解决问题的同时，再多迈进一步，让潜能生在顺利完成第一步的基础上，进行适时的提高；第3 题则是提升性练习，对于学优生而言，通过灵活变通就可以解决，而对于潜能生与中等生而言，因为有了前面运用公式的基本练习，这道题仍具有一定的挑战性，能培养他们灵活运用知识的高阶思维。这样的题组设计由易到难、由浅入深，让学生能一步一个台阶，促使数学思维拾级而上。

二、设计联系性的题组作业，让学生思维连点成线

数学是一门逻辑性很强的学科，其内部知识间的联系是十分紧密而严谨的。因此，数学教师应将同质、同类的问题整合为一个题组，以旧知识为起点，逐步推向新的高度，打通新旧知识之间的联系，促使学生在原有知识的基础上实现自然的思维进阶，亲身经历新知识的形成过程；应使学生在“润物细无声”中获得新知识的生长点，成功地将有联系的知识、方法等同化、顺应到原有的认知结构之中，实现思维自然的连点成线。

例如，在教学人教版数学教材五年级下册“分数”单元内容时，分数这个知识点相对小学生而言是比较抽象的，他们在解决实际问题时会遇到一定的困难。因此，在校本作业中，笔者设计了这样的一个题组：

明明有一瓶250 毫升的酸奶，冬冬有一瓶200 毫升的酸奶：

1. 明明和冬冬都说他们喝了酸奶的1/5，他们喝得一样多吗？

2. 假如明明和冬冬都喝了50 毫升，你能算出他们各喝了自己那瓶酸奶的几分之几吗？

3. 如果明明和冬冬已喝的酸奶一样多，那他们各喝了自己那瓶酸奶的几分之几？

这样的题组，其相同的本质就是明明和冬冬的酸奶是不一样的，而都要弄清所喝的酸奶量与其相对应的分率。第1 题中分率是相同的，都是1/5，但是各自相对应的单位“1”却是不一样的，因而喝的量也是不一样的；第2 题中两人喝的酸奶量是相同的，但是因为各自的单位“1”不一样，所以其所对应的分率也是不同的；第3 题中假设两人喝的酸奶量是一样的，要求的是其所对应的分率。显然，这样的题组设计，巧妙地将不同的问题联系在一起，通过对比，让学生感悟到“万变不离其宗”的数学魅力，促使学生能紧紧地抓住分数的基本特征，找准量与率相对应的关系，有效地解决此类问题。

三、设计变式性的题组作业，让学生思维走向深刻

小学生思维发展还不够成熟，他们常常会受到某些情境、素材中相关因素的干扰而形成思维定式。在课堂教学中，尤其是校本作业的设计，教师应立足于学生的思维现状，渗透变式思想，设计一些变式性的题组，有意识地培养学生数学思维的严谨性、敏捷性和灵活性。教师可着手于数学本质特征不变的基础，多元化、多维度地改变问题、情境或数据等，引导学生在变式情境、问题或数据中克服思维定式。变式性的题组作业的训练，是渗透变式思想的主要路径和方法，一题多变、一题多解、多题同解、多题同质，这种将变式思想与题组作业的深度融合，能有效促使学生的数学思维走向深刻。

例如，在教学人教版数学教材六年级上册“圆的面积”之后，笔者在校本作业中设计了以下一组题目：

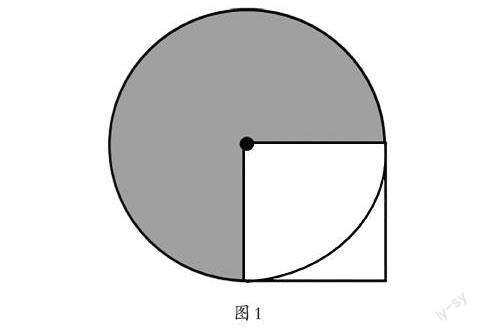
如图1，你能解决以下问题吗？

1. 如果图中正方形的边长是4 dm，求出阴影部分的面积是多少平方分米？

2. 如果图中正方形的面积是16 dm2，求出阴影部分的面积是多少平方分米？

3. 如果37.68 dm2是图中阴影部分的面积，那么正方形面积又是多少平方分米？

设计这样一组变式题目，其目标很明确：学生在解决第1 道题时，是数学知识方法的正迁移，直接运用所学的“圆的面积”计算公式得以解决。其中，正方形的边长4 dm 其实质就是圆的半径，因而学生通过这个间接告知的条件求出圆的面积，再用圆面积减去正方形的面积即可。第2 道题明确是变式，并没有直接告诉学生边长的大小，学生也就无从直观获得圆半径的大小，而学生习惯于正向思维，这样的变式题目无疑是颠覆了学生原有的认知，逼着学生转换思维角度来思考问题。该题将学生的思维置放于“变式场域”中，促使学生“绞尽脑汁”地发现：因为圆的半径就是正方形的边长，由于S = r2 = 16 dm2，可直接将r2 = 16 dm2代入圆的面积公式，从而推理出“S = πr2 = 3.14×16 = 50.24 dm2。笔者并没有在此变式上止步，而是又设计了第3 道变式题，又一次倒逼学生先通过阴影部分的面积是整个圆的3/4 而求出圆的面积是50.24 dm2，再反过来通过“S = πr2”计算公式而倒推出r2 = 50.24 ÷3.14 = 16 dm2，也就算出了正方形的面積。这样的变式题组设计，促使学生从“ 正迁移”走向“ 逆思维”。当“逆思维”同化到学生已有的认知结构时，教师又启发学生走向更为深刻的“逆思维”，正反变式、纵深推进，促使学生进一步巩固了圆的面积公式，更让学生经历了认知结构从建构到破构再到重构的过程。

四、设计开放性的题组作业，让学生思维得以创新

数学本身是一门严谨性、创造性强的学科。校本作业作为学生数学思维的训练场，更应该立足于培育学生的创新精神而设计一些具有开放性的题组。这样的题组可有效点燃学生创造的火花，激发学生进行数学探究的欲望，促使学生能从不同角度、不同立足点发现、提出、分析并能顺利地解决问题，提升学生解决实际问题的能力，让学生的求异思维、发散思维和创新思维得以培育。

例如，在教学人教版数学教材五年级下册“长方体和正方体表面积”这一内容之后，为了提升学生灵活运用所学数学知识解决问题的能力，笔者在校本作业中设计了一组开放性的题组：

1. 农民伯伯准备将一块长是10 dm，高是8 dm，宽是6 dm 的长方体木头锯成两块长方体，你能算出锯后的表面积会增加多少平方分米吗？

2. 农民伯伯准备将两块长是10 dm，高是8 dm，宽是6 dm 的长方体木头组接成一块大长方体，你能算出拼接后的表面积会减少多少平方分米吗？

3. 明明在家里搭积木，他将16 个棱长是1 cm 的小正方体积木拼搭成一个更大的长方体，你能算出拼搭后长方体的表面积是多少平方厘米吗？

显然，这一题组中题目的设计都比较开放，能激发学生调用已有知识经验灵活解决新问题的积极性。第1 题中，有的学生可能是沿着长10 dm 锯开，所增加的表面积便是两个侧面积；有的学生可能是沿着高8 dm 锯开，所增加的表面积便是两个底面积；有的学生可能是沿着宽6 dm 锯开，所增加的表面积便是前后两个面的面积和。同理，学生在解答第2 题时，也从不同的角度进行拼接，有的学生将上下面重叠，有的学生将左右面重叠，有的学生将前后面重疊。不同的拼接方法，其表面积减少的结果也是不一样的。前两道题的一锯一叠，其表面积则是一增一减，让学生通过对比练习，对于此类题型有一个完整的建构。同时，这种开放性的视角，也促使不同学生的数学解决问题能力得到不同的发展。而第3 题则是小正方体不同的拼组法，能进一步有效地培养学生的创造性思维。事实表明，这种开放式题组的训练，能高效地调动学生思维的积极性，高品质地发展学生的创新思维。

“双减”背景下，要真正减轻学生的学业负担，就应提高校本作业的质量。而题组作业的设计，因其在突出数学知识重点、突破难点、厘清知识易混点等方面有着显著而独特的现实价值，应引起广大小学数学教师的重视。实践证明，设计层次性、联系性、变式性和开放性的题组作业，能恰到好处地激发学生积极主动去探究、分析、反思与创造，高品质地让学生的思维拾级而上并走向深刻，实现“减负而减质”“减负更要提质”的育人效果，助推“双减”落地生根。

课题项目：本文系福建省教育科学“十四五”规划2021 年度专项教改课题“‘双减政策下小学数学校本作业设计的实践研究”的研究成果。课题编号：Fjjgzx21-004。

（责任编辑：杨强）