基于改进的SMO 永磁同步电机无位置传感器研究*

李亚轮 黄 波 陈贺军 舒 强

（1.上海工程技术大学 上海 201620）（2.上海同驭汽车科技有限公司 上海 201806）

1 引言

内置式永磁同步电机由于质量轻、效率高、最大转矩电流比高、弱磁范围宽等优点，在纯电动汽车、汽车零部件（EHB、EPS、EPB 等）、船舶驱动、航空航天、电子电器等方面应用广泛［1～2］。永磁无刷电机控制器一般都安装转子位置传感器、电机转速传感器等各种传感器件，这样不仅增加成本，各种传感器故障还会导致电机无法正常工作等各种问题［3～4］。为解决上面的问题，近年来无位置传感器的永磁同步电机发展迅速，并逐步运用到各个领域。电机无位置传感器控制策略一般有龙伯格观测器法、模型参考自适应系统（MRAS）、拓展卡尔曼滤波法、滑模观测器（SMO）法［5～8］。滑膜控制由于对电机内部参数变化不明显和外部输入信号抗干扰能力强，故在电机控制领域广泛应用。文献［9］采用传统的滑膜观测器算法，采用符号函数sign（h）来估计反电动势，并且基于反正切函数可以对转子的位置进行估计，但是这样会导致电机高频抖振以及转子位置估计不精确等问题。文献［10］中提出用连续的sat函数取代不连续的符号函数，显然避免了高频抖振的问题，但是在低速下转子位置估计的精确度并不高。文献［11］中用反正切函数获取转子位置来转子估计的位置信息，一定程度上提高了转子获取位置信息估计的准确性，但并不能满足实际需求。文献［12］用传统的高频信号注入法，通过电感饱和效应构造“饱和凸极”来估计永磁同步电机的转子位置，并且在电流环反馈和位置观测环节使用低通滤波器，但是这样会导致电流相应和转子位置估计的响应延迟。针对上面的问题，本文依然提出用连续的双曲正弦函数取代不连续的符号函数，并且通过锁相环的方法取代传统的反正切和单相锁相环得到转子位置信息的方法。利用构造李雅普诺夫稳定性函数判定控制系统的稳定性。通过Matlab/Simulink 仿真验证证明所提出的对永磁同步电机的控制策略，可以精确地估算出无位置传感器的转子位置和转速，以及可以有效的减缓高频下的抖振问题和提高系统的鲁棒性。

2 IPMSM无位置传感器数学模型

为了更为准确地获取转子的位置和速度的信息，将内置式永磁同步电机在两相静止坐标系（ɑ-β）下的数学模型改成电流模式如下：

3 滑膜观测器设计

3.1 传统滑膜观测器设计

由于内置式永磁同步电机数学模型的扩展反电动势中包含有转子位置以及转速信息，可构建滑膜观测器对扩展反电动势进行观测分析，得到估计的转子位置以及转速等信息［13～14］。因此可以构建滑膜观测器如下：

由式（3）与式（4）相减可得到定子电流的估计方程，如下：

定义滑膜面函数为

设计滑膜控制率为

根据Lyapunov 稳定性方程可知，若要确保滑膜系统大范围内渐进稳定，有，当观测器状态变量达到滑膜面之后，即，，滑膜观测器状态将会一直保持在滑膜面上。由式（6）可以得到扩展反电动势的估计值为

根据估计的扩展反电动势的值，并加入对相位滞后的补偿，可以根据反正切函数得到转子的位置以及估计转速，即：

一般加入转子位置补偿来弥补低通滤波器的加入造成的扩展反电动势估计值发生的相位误差，常用补偿算法为

由以上分析可知，基于传统的SMO 算法永磁同步电机无位置传感器的控制原理图如图1所示。

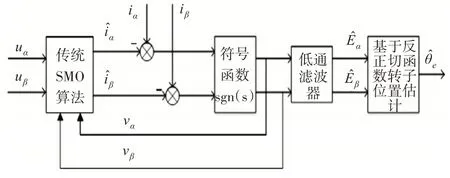
图1 传统SMO算法无位置传感器控制原理图

以上即为基于传统的滑膜观测器获取转子的位置信息，此观测器采用不连续的符号函数，由于开关函数的不连续性，通过低通滤波器的滤波作用，滤除切换过程中产生的高频信号，可以有效减小系统的抖振。但是，加入滑膜观测器之后，会导致扩展反电动势的相位滞后，通过相位补偿环节来提高转子位置估计的准确性［15］。但增加了系统复杂度，估计转子位置与估计转速精度也不高且会伴有噪音。于是，通过对滑膜观测器进行改进，并对转子位置的获取方法进行改进，可有效地解决以上问题。

3.2 新型的滑膜观测器设计

为了解决上述问题，本节对传统的滑膜观测器进行改进，设计一种新型的二阶滑膜观测器，并且引用锁相环来获取转子位置，所设计的新型二阶滑膜观测器与一阶滑膜观测器相比不仅可以有效地消除抖振问题，而且可以不使用低通滤波器就可以解决转子位置相位滞后问题。

设计新型的SMO 首先选取零点处光滑连续的S型饱和双曲正切函数g（s）=tanh（t），取代原点处不连续的符号函数sign（t），来提高滑膜观测器的品质。双曲正切函数与sigmoid（t）函数及sat（t）函数相比可降低处理器性能和降低运算时间。

双曲正切函数表达形式如下：

双曲正切函数与sigmoid函数在a取3和8时及符号函数对比如图2所示。

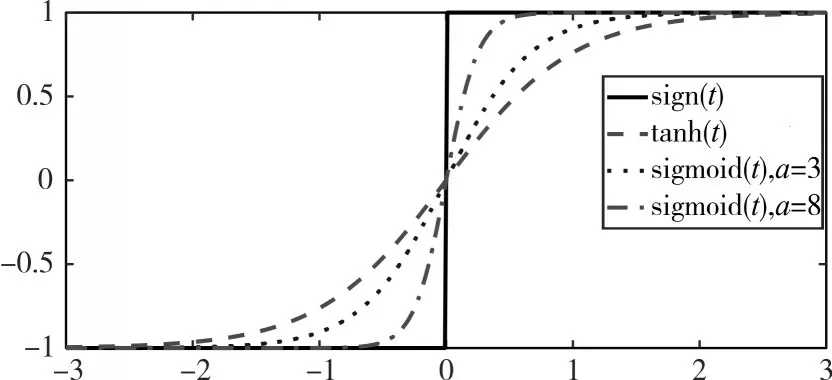
图2 各曲线函数对比图

用双曲正切函数代替式（3）中的符号函数，可得基于双曲正切函数的SMO设计为

1）定义积分滑膜面为

2）新型二阶SMO控制率设计如下：

系统在滑动模态时，表贴式永磁同步电机电流误差趋近于0，根据得等效控制为

为了满足系统可达性条件，在滑膜面S(x，t)=0 以外的所有运动点都将在有限时间内到达滑膜面，即s·＜0，为提高观测器的状态变量趋近滑膜面时的品质，缩短趋近阶段的运动时间，尽可能避免内部参数变化和外部信号输入造成的影响，这里选取指数趋近律如下：

=-εsgn(s)-qs，并且ε，q＞0

由式（14）可得：

综上由式（14）得，滑膜变结结构控制律为

3）系统稳定性分析：

根据李雅普诺夫稳定性判据，系统大范围内趋近稳定的条件为

将式（17）代入上式得：V=-ε|s|-ks2。

通过对上式分析可得如下，当k≥0且ε≥0，s≥0 时，ε|s|≥0，ks2≥0 ；k≥0且ε≥0，s≤0时，ε|s|≥0，ks2≥0；

通过上式的分析可知，无论s 取何值时，都有≤0；

故系统在大范围内是渐进稳定的。

本节采用单相锁相环来提取转子位置信息，可以很大程度上提高转子位置的估计精度。如下图3所示为基于PLL的实现转子位置获取框图。

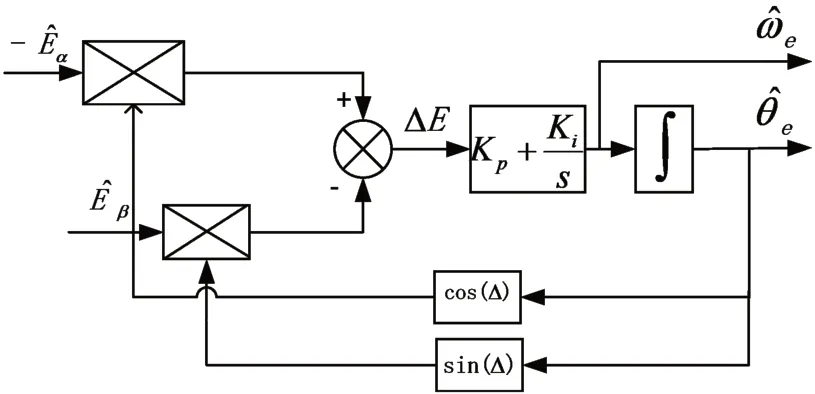
图3 基于PLL的实现转子位置获取框图

估计扩展反电动势在经过低通滤波器后输出的运算关系如下：

在电机仿真与实际运转的过程中，转子的实际位置与估计位置非常接近，即

|θe-|趋近于0，故可近似认为

采用PI 对转子位置误差Δθe进行调节之后可以得到估计转速，再对估计转速积分可以得到估计转子位置，基于PI控制器的等效框图如图4所示。

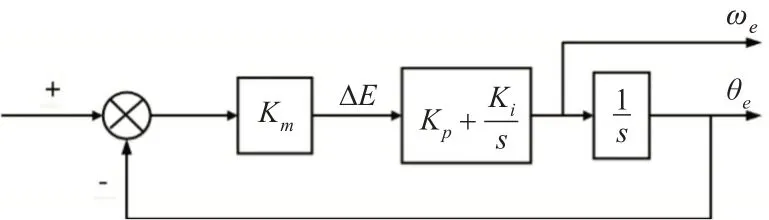
图4 PI控制器的等效框图

由上图得传递函数：

以典型的二阶系统来整定：

其中ωn为带宽调节参数，，；选择合适的ξ，ωn确定出理想的频率特性，进一步确定出锁相环中的PI 整定参数，对比实际信号与估计信号差别；

基于新型的SMO结构示意图如图5所示。

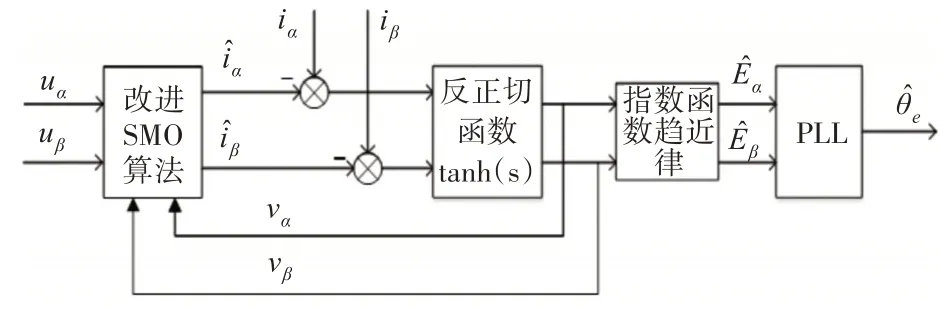
图5 改进SMO控制算法框图

4 仿真模型建立以及结果分析

基于改进后SMO 的三相PMSM 无位置传感器整个系统控制实现框图如图6所示。

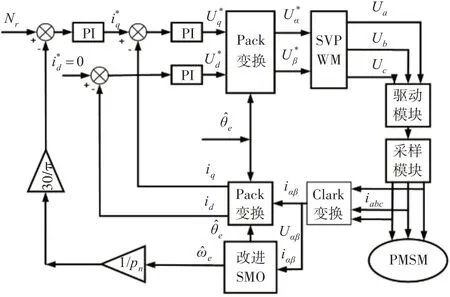
图6 改进SMO无位置传感器系统

基于改进的SMO 的三相IPMSM 无位置传感器控制策略实现框图在Matlab/Simulink 软件中搭建仿真模型，其仿真模型中永磁同步电机的参数如表1所示。

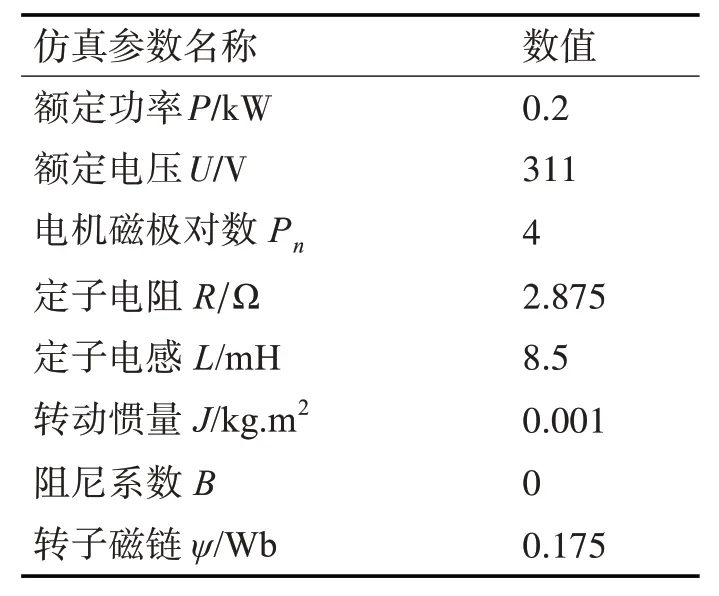
表1 表贴式永磁同步电机模型仿真参数

由于搭建的模型是连续的且较为复杂，为避免仿真过程中仿真时间过长及仿真过程中变量超调过大，故对滑膜观测器的参数设置为C=60，ε=200，k=300，对传统滑膜观测器控制及新型滑膜观测器两种情况下三相IPMSM 矢量控制系统的仿真结果如下：仿真选取了前30ms 转子位置跟踪仿真图，转速仿真跟踪选取前50ms；图7 所示为传统滑膜观测器转速跟随响应曲线，从图中可知给定转速1500r/min 下，响应超调为80r/min，图8 所示为转速误差保形拟合误差曲线，由图可知转速估计误差在30r/min附近。

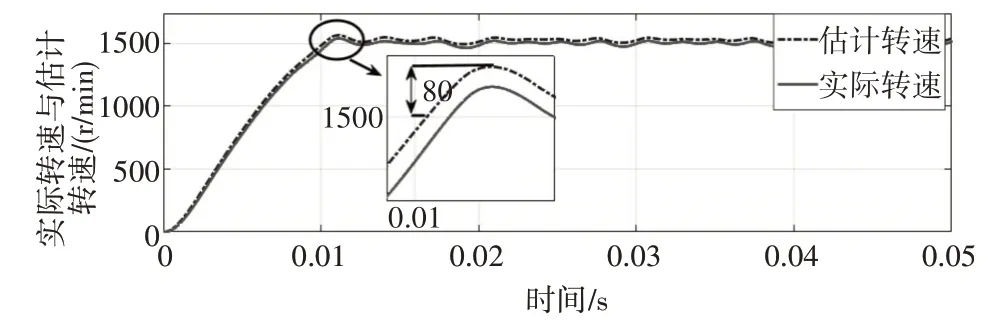
图7 传统SMO转速跟随曲线

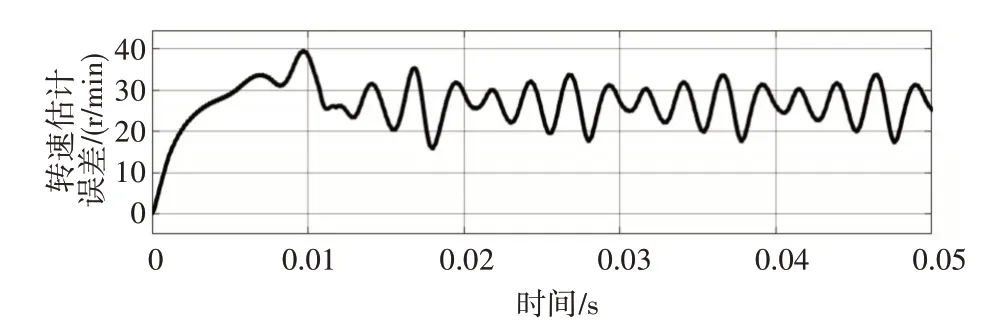
图8 传统SMO转速估计误差

估计转子估计位置与转子实际值差别较大，这是因为在低速区间滑膜控制算法不能准确估计出转子实际位置。且在高速区，实际转速与估计转速有一定差值，约为30r/min，这是由于传统滑膜观测器鲁棒性较差的原因。

改进的滑膜观测器算法转速响应仿真结果如图9 所示，响应超调为20r/min，且响应时间相近；图10 为改进的滑膜观测器转速跟随误差保形拟合误差曲线，由图可知，估计转速与实际转速变化趋势与数值基本吻合，转速误差在±5r/min 随着转速的增大，滑膜控制算法精度渐高，转子位置估计值与实际值更接近。

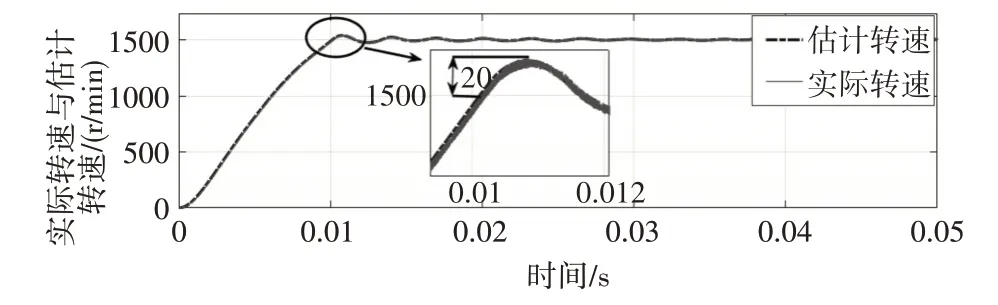
图9 改进SMO转速跟随曲线

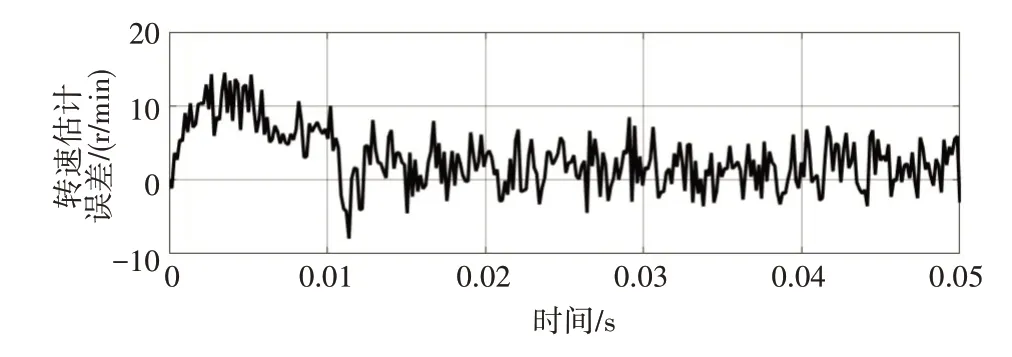
图10 改进SMO转速估计误差

如图11 为传统滑膜观测器控制算法估计的转子位置与实际位置仿真跟踪图，由局部放大图可知估计转子误差在1.6rad/min，时间延迟约为0.05%秒，图12 为改进SMO 控制算法估计的转子位置与实际位置跟踪图，图12较图11相比，实际转子位置跟踪估计转子位置效果更好；转子估计误差低速和高速段相差不大，为0.7rad/min左右；时间延迟约为0.02%秒左右。

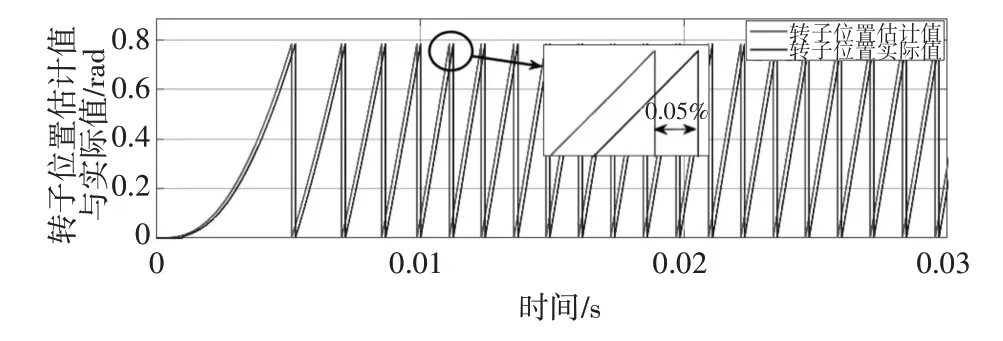
图11 传统SMO转子位置跟踪图

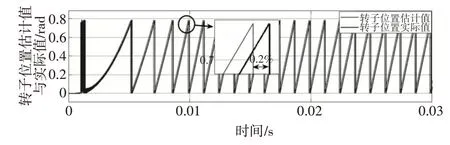
图12 改进SMO转子位置跟踪图

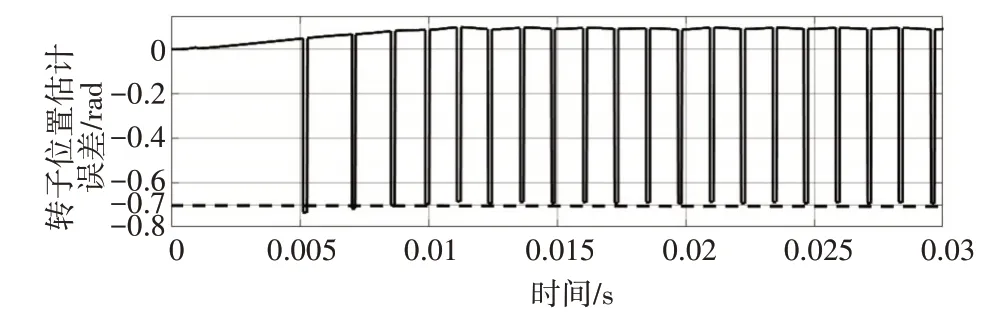
图13 改进SMO转子位置估计误差

5 结语

综上所述，采用传统滑模观测器算法估计出的转速，抖动最大值约为30 转，转子位置估计延迟约为0.5%秒。转速稳定时，采用改进滑模观测器算法估计出的转速抖动最大值约为8 转，转子位置估计延迟约为0.2%秒。转子估计精确度改进SMO 与传统SMO 相比提高250%。本文所提采用双切正弦函数和指数趋近律的二阶滑模观测器算法能更好的抑制抖振，使估计值误差更小，更切合实际值，具有实际应用价值。